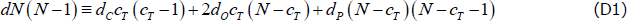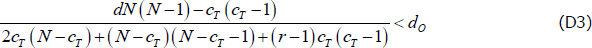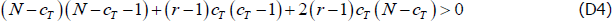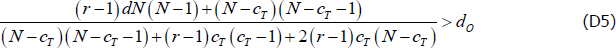RDP 2018-01: A Density-based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market Appendix D: Process for Constructing Simulation Draws

The simulations that allow missing links within the true-core block require the imposition of three inequality constraints on the densities of the true-core, true-periphery and true off-diagonal blocks. The simulations then draw randomly from all possible networks that satisfy these constraints. As discussed in Section 6, the inequality restrictions are:

1. d_C > d_O
2. d_O > d_P
3. 1 − d_C < d_P

For simulations that do not allow missing links within the true-core block, d_C = 1 and the first and third inequality restrictions become obsolete.

Imposing these restrictions is based on the following identity (c_T is the true size of the core):

The left-hand side is the number of links in the simulated network, which is known since we parameterise the simulations based on the observable average size and density of the networks formed from our data. The right-hand side decomposes this into the links in each block (when the banks are split into the true core and true periphery).

To impose the third restriction, we draw r from unif(0, 1) and set d_C = (r – 1)d_P + 1 (for simulations in which d_C = 1, we set r = 1). Substituting this into Equation (D1) then gives us a linear relationship between d_O and d_P (since {d, N, c_T, r} are already parameterised), which we can then use to impose the other inequality restrictions.

To ensure d_P > 0 (required by definition of a ‘density’):

Note that dN(N − 1) − c_T(c_T − 1) >0 with our parameterisations.

To ensure d_O > d_P:

To ensure d_C > d_O, the relevant inequality depends on the values of the other parameters. If the following holds:

then the relevant inequality is (the numerator is always positive with our parameterisations):

If Equation (D4) does not hold, then Equation (D5) is not necessary.

Denote the left-hand sides of Equations (D2), (D3) and (D5) as UB₁, LB, and UB₂, respectively. Then if Equation (D4) holds, d_O is drawn from unif(LB, min{UB₁, UB₂}). If Equation (D4) does not hold, d_O is drawn from unif(LB, UB₁).

Finally, substituting d_C = (r − 1)d_P + 1 and the draw for d_O into Equation (D1) gives the draw for d_P, which is then substituted into d_C = (r − 1)d_P + 1 to give the draw for d_C.

With the densities of each block drawn, the locations of the links within each block are determined using an Erdős-Rényi model (ensuring the off-diagonal blocks retain the necessary row/column regularity).