RDP 2018-01: A Density-based Estimator of Core/Periphery Network Structures: Analysing the Australian Interbank Market Appendix C: The Two-step Cucuringu et al (2016) Estimator
February 2018
- Download the Paper 1,628KB
Cucuringu et al (2016) propose a two-step process for estimating the core/periphery split of a network. The first step uses some criteria to rank the nodes by ‘coreness’. Cucuringu et al propose several ranking criteria, including ranking nodes by their degree. Given this ranking, the second step then chooses where to draw the line between core and periphery.
The second step uses an error function similar to our DB estimator. The main differences are that missing links in the off-diagonal blocks are all treated as errors (rather than just requiring row or column regularity), and that they put bounds on the possible core sizes. While these bounds can be set to the bounds of the network (i.e. [0, N]), Cucuringu et al find that their two-step estimator performs poorly without more restrictive bounds.[33]
The upside of their process is that it is potentially more efficient. For any given ranking, determining the CP split requires evaluating at most N + 1 possible splits (i.e. possible core sizes from zero to N). If the first step also requires only a small number of calculations (e.g. ranking based on degree), then an optimisation algorithm for the Cucuringu et al (2016) estimator will be much faster than our DB estimator (with either a global search (2N possible CP splits) or a greedy algorithm with multiple starting points).
However, if the global optimum is not one of the CP splits over which the second step searches, the Cucuringu et al (2016) estimator cannot find the global optimum. So the Cucuringu et al estimator is, at best, only as accurate as our DB estimator with a global search. While this result may not hold when using a greedy algorithm with the DB estimator, the performance of the Cucuringu et al estimator will always be bounded by the quality of the first-step ranking.
To give an example of the problem, we ran the Cucuringu et al (2016) estimator on simulated data constructed using a method similar to the one outlined in Section 6 (Figure C1). In this simulation, we set dC = 1 and dO = dP; this is done not for realism but to highlight the potential extent of the problem. For simplicity, we rank nodes by their degree as the first step.[34] And to highlight the issues associated with the two-step procedure (as opposed to differences resulting from the different error functions), we adjust the error function used in the second step to match Equation (5).
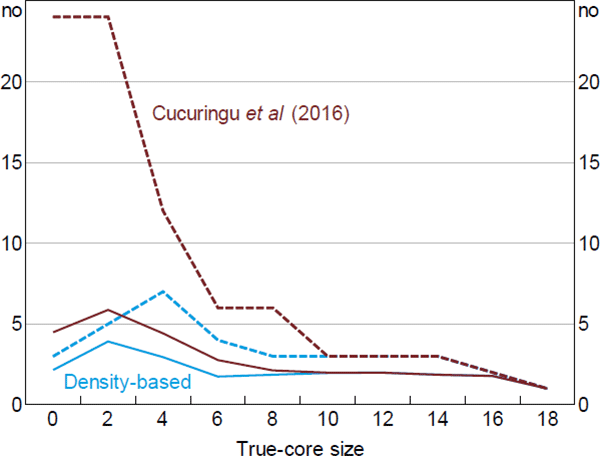
Note: The version of the Cucuringu et al (2016) estimator used here ranks nodes by their degree as the first step, and adjusts the second step to be consistent with the Craig and von Peter (2014) definition of a core/periphery structure
When the true-core size is large, the Cucuringu et al (2016) estimator performs as well as the DB estimator. This is expected since it is when the true-core size is large that ranking nodes by their degree is more likely to be an accurate measure of their ‘coreness’. When the true-core size is small, the Cucuringu et al estimator exhibits a larger average error than the DB estimator. The difference between estimators is starker when comparing the tails of their error distributions, with the 99th percentile from the Cucuringu et al estimator being comparable to the worst-performing estimators in Section 6.
Interestingly, Cucuringu et al (2016) also find that a second-step error function that focuses on the number of errors (i.e. one akin to the CvP estimator) often leads to ‘disproportionately-sized sets of core and peripheral vertices [nodes]’ (p 856). But they provide no explanation of the reason. Our theoretical analysis fills this gap.
Footnotes
Since our DB estimator does not require any bounds, the need for more restrictive bounds could be due to their two-step procedure. [33]
While Cucuringu et al (2016) provide ranking criteria that may be more accurate, the point of this exercise is to show the potential extent of the problem, not to evaluate the best version of their estimator. [34]