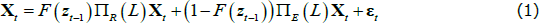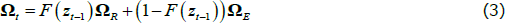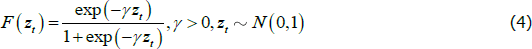RDP 2017-06: Uncertainty and Monetary Policy in Good and Bad Times
3. Modelling Nonlinear Effects of Uncertainty Shocks
October 2017
We estimate the impact of uncertainty shocks on real economic outcomes using a nonlinear VAR model. The vector of endogenous variables Xt includes (from the top to the bottom) the S&P 500 stock market index, an uncertainty dummy based on the VXO, the federal funds rate, a measure of average hourly earnings, the consumer price index, hours worked, employment, and industrial production.[4] These variables are expressed in logs, except the uncertainty dummy, the policy rate, and hours.[5]
We use monthly data covering the period July 1962 to June 2008. We cut the sample in June 2008 to avoid modelling the period that started with the Lehman Brothers bankruptcy and the acceleration of the 2007–09 financial crisis in September 2008. Such acceleration led the Fed to quickly cut the federal funds rate to zero, and maintain the rate at that level until December 2015. We interpret this period as a third regime, the modelling of which would render the estimation of our nonlinear framework more complex.
As in Bloom (2009), the uncertainty dummy takes the value of one when the HP-detrended VXO level rises 1.65 standard deviations above its mean, and zero otherwise.[6] This indicator function is employed to ensure that identification comes from large, and likely to be exogenous, jumps in financial uncertainty that are unlikely to represent systematic reactions to business cycle movements. Given that we base our identification strategy on well-known uncertainty-inducing events, the effects of uncertainty shocks documented in this paper should be seen as responses to extreme jumps in uncertainty rather than a characterisation of the general effects of uncertainty in the economy.[7] In addition, these extreme jumps are largely associated with bad news. This makes our definition of uncertainty shocks slightly different from that commonly used in theoretical studies, that is, uncertainty shocks are usually defined as shocks to the second moment (variance) of the probability density distribution of a given variable. Our identification approach focuses instead on the first moment (shocks to the level) of the VXO. However, in line with the definition of the VXO as being an index of market-implied volatility, we interpret these shocks as shocks to the volatility of the US stock market induced by ‘extreme bad events’. We believe that our dummy-based approach offers a better identification than the usual orthogonalisation of the VAR residuals of the VXO itself. However, identification of causal effects is hard, and our uncertainty shocks may still be picking up endogenous responses that are not captured by our STVAR model.[8]
Figure 1 shows the VXO index along with the NBER recession dates and the identified uncertainty shocks. The sixteen uncertainty-inducing episodes are equally split between recessions and expansions. Noticeably, all recessions are associated with significant spikes in the volatility series. This is in line with a key fact about uncertainty summarised by Bloom (2014), that is, macro uncertainty rises in recessions.
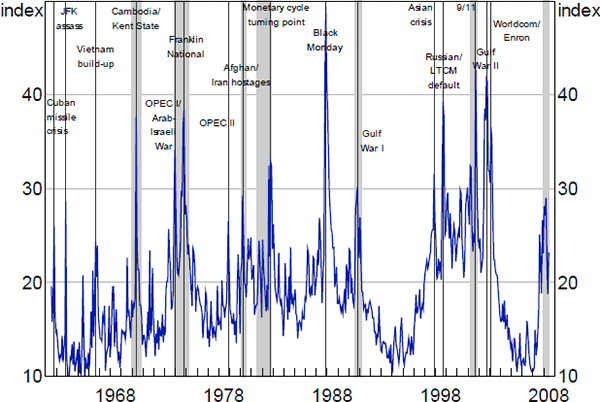
Notes: Chicago Board Options Exchange (CBOE) VXO index of implied volatility on a hypothetical at the money S&P 100 30 days option from 1986 onward; pre-1986 returns' volatilities obtained by computing the monthly standard deviation of the daily S&P 500 index, and normalised to the same mean and variance as the VXO index when they overlap from 1986 onward; the variance is annualised and the index expresses volatility in percentage points; vertical lines denote uncertainty shocks as defined in the paper; shading denotes NBER recessions
Sources: Authors' calculations; Chicago Board Options Exchange; National Bureau of Economic Research
The STVAR model assumes that the vector of endogenous variables can be described as a combination of two linear VARs, one describing the economy in bad times and the other in good times (for a detailed presentation, see Teräsvirta, Tjøstheim and Granger (2010)). In particular, the vector of endogenous variables Xt is modelled with the following STVAR:
In this model, F(zt) is a logistic transition function that captures the probability of being in a recession, γ is the smoothness parameter, zt is a transition indicator, ∏R and ∏E are the VAR coefficients capturing the dynamics of the system in recessions and expansions, εt is the vector of reduced-form residuals with zero mean and time-varying, state-contingent variance-covariance matrix Ωt, where ΩR and ΩE are covariance matrices of the reduced-form residuals estimated during recessions and expansions.
Recent applications of the STVAR model to analyse the US economy include Auerbach and Gorodnichenko (2012), Bachmann and Sims (2012), Berger and Vavra (2014), and Caggiano et al (2015), who employ it to study the effects of fiscal spending shocks in good and bad times, and Caggiano et al (2014) and Caggiano, Castelnuovo and Figueres (2017), who focus on the effects of uncertainty shocks on unemployment in recessions. The key advantage of the STVAR model relative to threshold VARs is that with the latter we may have relatively few observations for recessions, which makes estimates unstable and imprecise. In contrast, estimation and inference for each regime in the STVAR is based on a larger set of observations.[9]
Conditional on the standardised transition variable zt, the logistic function F(zt) indicates the probability of being in a recessionary phase. The transition from one regime to another is regulated by the smoothness parameter γ, that is, large (small) values of γ pimply abrupt (smooth) switches from one regime to another. The linear model à la Bloom (2009) is a special case of the STVAR, obtained when γ = 0; which implies ∏R = ∏E = ∏ and ΩR = ΩE = Ω. We make sure that the residuals of the uncertainty dummy equation are orthogonal to the other residuals of the estimated VAR by imposing a Cholesky decomposition of the covariance matrix of the residuals. Hence, the ordering of the variables admits an immediate response of industrial production and employment, as well as prices and the federal funds rate, to an uncertainty shock. However, these variables do not contemporaneously affect uncertainty. This assumption is consistent with that of exogeneity of the spikes of the VXO identified with the strategy described above. It is also consistent with the theoretical model of Basu and Bundick (2017), in which first-moment or non-uncertainty shocks have almost no effect on financial volatility. We include, however, the S&P 500 index before our uncertainty indicator to control for the impact of the stock market itself on financial volatility.
A key role is played by the transition variable zt (see Equation (4)). Auerbach and Gorodnichenko (2012), Bachmann and Sims (2012), Berger and Vavra (2014), Caggiano et al (2014), and Caggiano et al (2015) use a standardised moving average of the quarterly real GDP growth rate as transition indicator. Our paper deals with monthly data. Similarly to Caggiano, Castelnuovo and Figueres (2017), we employ a standardised backward-looking moving average involving 12 realisations of the month-to-month growth rate of industrial production.[10] Another important choice is the calibration of the smoothness parameter, whose estimation is affected by well-known identification issues (see the discussion in Teräsvirta et al (2010)). We exploit the dating of recessionary phases produced by the National Bureau of Economic Research (NBER) and calibrate γ to match the frequency of the US recessions, which amounts to 14 per cent of our sample. Consistently, we define as ‘recession’ a period in which F(zt) > 0.86, and calibrate γ to obtain Pr(F(zt) > 0.86) ≈ 0.14.[11] This metric implies γ = 1.8. In Appendix B, we show that our results are robust to alternative calibrations of the smoothness parameter γ.
Figure 2 plots the transition function F(zt) for the US post-WWII sample and superimposes the NBER recessions dating. Two observations are in order. First, the transition function peaks with a slight delay relative to the NBER recessions. This is due to our use of a backward-looking transition indicator. This choice enables us to compute the transition probability by using observed values of industrial production, and thus it allows us to account for a switch from one regime to another conditional on the evolution the system after the shock. To put it simply, using a centred moving average would prevent us from calculating GIRFs. Second, the volatility of F(zt) drops when entering the Great Moderation period, that is, 1984–2008. This might suggest the need to re-optimise the calibration of γ to better account for differences in the regime switches occurring in the two sub-samples 1962–83 and 1984–2008. When we do this, the calibration of our smoothness parameter for the two periods reads 1.6 and 1.7 (for capturing the 20 and 8 per cent frequencies of NBER recessions in the two sub-samples).[12] Such calibrations are quite close to the one we employ in our baseline exercise (where γ = 1.8). Estimations conducted with these two alternative values lead to virtually unaltered results (Appendix B). All in all, our transition probability closely tracks the downturns of the US economy.
Since any smooth transition regression model is not identified if the true data generating process is linear, we test the null hypothesis of linearity against the alternative of a logistic STVAR for our vector of endogenous variables. We employ two tests proposed by Teräsvirta and Yang (2014). The first is a LM-type test, which compares the residual sum of squares of the linear model with that of a third-order approximation of the STVAR framework. The second is a rescaled version of the previous test, which accounts for size distortion in small samples. Both test statistics strongly reject the null hypothesis at any conventional significance level. A description of the tests is provided in Appendix A. We also show that the linear impulse responses to an uncertainty shock (calculated with our model when γ = 0) are different from the nonlinear ones (Appendix B).[13]
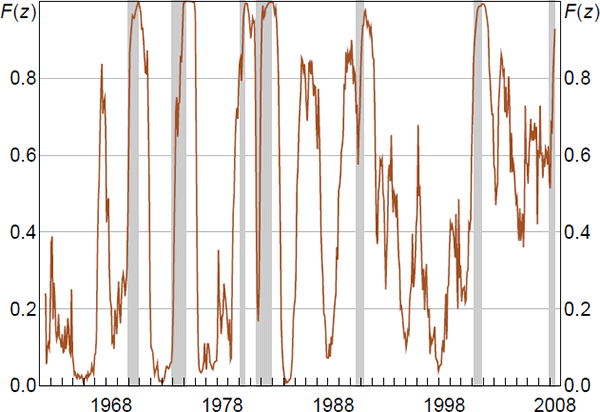
Notes: Transition function F(z) computed by employing the standardised moving average (12 terms) of the month-on-month growth rate of industrial production; shading denotes NBER recessions
We estimate the STVAR model with six lags, a choice supported by standard information criteria as regards the linear version of the VAR model, for which an extensive literature on optimal lag selection in VARs is available. Given the high nonlinearity of the model, we estimate it by employing the Markov Chain Monte Carlo simulation method proposed by Chernozhukov and Hong (2003).[14] The estimated model is then employed to compute GIRFs to an uncertainty shock.[15]
Footnotes
As recalled by Bloom (2014), Knight (1921) defined uncertainty as people's inability to form a probability distribution over future outcomes. Differently, he defined risk as people's inability to predict which outcome will be drawn from a known probability distribution. Following most of the empirical literature, we do not distinguish between the two concepts, and use the VXO-related dummy as a proxy for uncertainty. We acknowledge though that this indicator is a mixture of both risk and uncertainty. See Bekaert, Hoerova and Lo Duca (2013) and Rossi, Sekhposyan and Soupre (2016) for investigations that disentangle the effects of risk and uncertainty. [4]
Our model specification closely follows that in Bloom (2009), which we take as a starting point for our analysis. However, and unlike Bloom, we do not Hodrick-Prescott (HP) filter these variables, except the VXO series we use to compute the uncertainty dummy. As shown by Cogley and Nason (1995), HP-filtering may induce spurious cyclical fluctuations, which may bias our results. Exercises conducted with HP-filtered variables, as in Bloom (2009), returned results qualitatively in line with those documented in this paper. These results are available upon request and are consistent with the robustness check in Bloom (2009, Fig A3, p 679). [5]
We use the HP-detrended VXO series to construct the dummy variable for consistency with Bloom (2009). Using the non-filtered level of the VXO to construct the dummy delivers a similar set of shocks. Further, we check the robustness of our results to alternative uncertainty proxies (see Appendix B). [6]
Working with linear VARs, Furlanetto, Ravazzolo and Sarferaz (2014) identify uncertainty shocks using sign restrictions, while Caldara et al (2016) adopt a penalty approach. We leave the investigation of the properties of these approaches in a nonlinear STVAR context to future research. [7]
One example would be changes in forecasts for the real economy, which are not modelled as our specification already includes a large set of variables. Additionally, and as previously mentioned, our uncertainty proxy is likely a stand-in for a mixture of risk and uncertainty. These are important observations to bear in mind when interpreting our results. [8]
A simpler, alternative approach would be that of adding an interaction term involving uncertainty and an indicator of the business cycle to the otherwise linear model à la Bloom (2009). The resulting interacted VAR would have the potential to discriminate between responses to uncertainty in recessions/expansions. We prefer to model a STVAR for two reasons. First, it does not require us to take a stand on the features of the interaction term (e.g. number of lags, timing of the cross products). Second, it is much less prone to instabilities, a problem often affecting interacted VARs when involving interaction terms of order two or higher (for a discussion, see Mittnik (1990)). [9]
Appendix B discusses the robustness of our results to the use of the unemployment rate as transition indicator. [10]
This choice is consistent with a threshold value 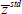 equal to −1.01, which corresponds to a threshold value for the non-standardised moving average of the growth rate of industrial production equal to 0.13 per cent. This last figure is obtained by considering the sample mean of the non-standardised growth rate of industrial production (in moving average terms), which is equal to 0.40, and its standard deviation, which reads 0.27. Then, its corresponding threshold value is obtained by ‘inverting’ the formula we employed to obtain the standardised transition indicator z, that is,
equal to −1.01, which corresponds to a threshold value for the non-standardised moving average of the growth rate of industrial production equal to 0.13 per cent. This last figure is obtained by considering the sample mean of the non-standardised growth rate of industrial production (in moving average terms), which is equal to 0.40, and its standard deviation, which reads 0.27. Then, its corresponding threshold value is obtained by ‘inverting’ the formula we employed to obtain the standardised transition indicator z, that is, 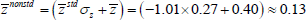 .
[11]
.
[11]
The calibration of γ in both sub-samples is lower than that for the full sample, despite the frequency of recessions being higher in the first sub-sample and lower in the second. This is because the calibration depends on the values taken by the transition variable (industrial production) in each period considered. Thus, there is no reason to expect the value of γ to be linear with respect to the frequency of recessions. [12]
A potential weakness associated with our modelling approach is the implicit assumption that the model parameters do not change over time (they change only across states of the business cycle). Modelling a time-varying parameters STVAR model is a possibility that we leave for future research. [13]
In principle, one could estimate the STVAR model via maximum likelihood. However, since the model is highly nonlinear and has many parameters, using standard optimisation routines is problematic. Under standard conditions, the algorithm put forth by Chernozhukov and Hong finds a global optimum in terms of fit as well as the distributions of parameter estimates. [14]
Following Koop et al (1996), our GIRFs are computed as follows. First, we draw an initial condition, that is, starting values for the lags as well as the transition indicator z, which provides us with the starting value for F(z). Then, we simulate two scenarios, one with all the shocks identified with the Cholesky decomposition of the VCV matrix, and another one with the same shocks plus δ > 0 corresponding to the first realisation of the uncertainty shock. The difference between these two scenarios (each of which accounts for the evolution of F(z) by keeping track of the evolution of industrial production) gives us the GIRFs to an uncertainty shock of size δ. Appendix A provides additional details on the algorithm we employed to compute the GIRFs. [15]