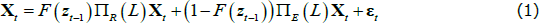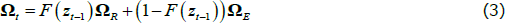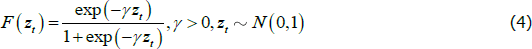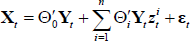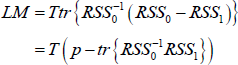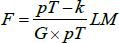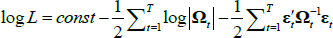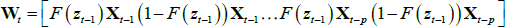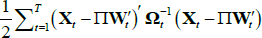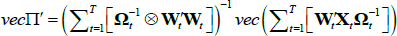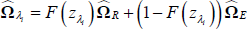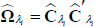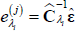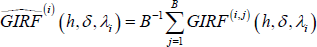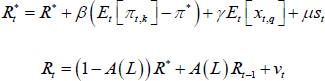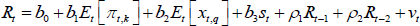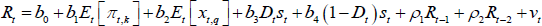Research Discussion Paper – RDP 2017-06 Uncertainty and Monetary Policy in Good and Bad Times
1. Introduction
Uncertainty shocks have recently been identified as one of the drivers of US business cycles (Bloom 2009; Bloom et al 2014; Jurado, Ludvigson and Ng 2015; Leduc and Liu 2016; Basu and Bundick 2017). This paper investigates the nonlinear effects of uncertainty shocks as well as the relationship between macroeconomic uncertainty and monetary policy in the United States. It does so by addressing three related questions: Are the effects of uncertainty shocks different in good and bad times? Is the stabilising power of systematic monetary policy in response to uncertainty shocks state-contingent? Do monetary policymakers respond to movements in uncertainty per se? We answer these questions by modelling a standard set of post-WWII US macroeconomic variables with a smooth transition vector autoregression (STVAR) model. This nonlinear framework allows us to capture the possibly different macroeconomic responses to an uncertainty shock occurring in different phases of the business cycle. We endogenously account for potential regime-switches due to an uncertainty shock by computing generalised impulse response functions (GIRFs) à la Koop, Pesaran and Potter (1996). Using GIRFs is important to correctly address the above mentioned questions because: i) uncertainty shocks that occur in expansions could drive the economy into a recessionary state, and ii) uncertainty shocks occurring in recessions may lead the economy to a temporary expansion in the medium term as uncertainty dissipates (Bloom 2009).
Our focus on nonlinearities is justified by two important stylised facts. First, most macroeconomic aggregates display an asymmetric behaviour over the business cycle (see, among others, Sichel (1993); Koop and Potter (1999); van Dijk, Teräsvirta and Franses (2002); Caggiano and Castelnuovo (2011); Morley and Piger (2012); Abadir, Caggiano and Talmain (2013); and Morley, Piger and Tien (2013)). Second, uncertainty features different dynamics in good and bad times. Micro- and macro-evidence of countercyclical uncertainty with abrupt increases in recessions is documented by Bloom (2009), Bloom et al (2014), Orlik and Veldkamp (2014), and Jurado et al (2015). Moreover, different indicators of realised volatility, often taken as a proxy for expected volatility in empirical analysis, are higher and more volatile in recessions (Bloom 2014, 2017).[1] In light of this evidence, one might expect uncertainty shocks to have different macroeconomic effects over the business cycle. Theoretical support for this intuition is provided by Cacciatore and Ravenna (2015). They work with a model featuring matching frictions in the labour market and show that deviations from efficient wage-setting (due to such frictions), combined with downward wage rigidities, imply a state-dependent amplification of the real effects of uncertainty shocks, and contribute to make uncertainty countercyclical. Importantly, this set of assumptions is more realistic than theoretically frictionless labour markets. Empirical support for Cacciatore and Ravenna's conjecture is provided by Caggiano, Castelnuovo and Groshenny (2014), Nodari (2014), Ferrara and Guérin (2015), Casarin et al (2016), and Caggiano, Castelnuovo and Figueres (2017). Our investigation complements these others by unveiling the interactions between uncertainty shocks and systematic monetary policy in different phases of the US business cycle. We study the US economy for two reasons. First, there is a reasonably-established literature on the linear effects of uncertainty shocks in the United States. This allows us to focus on nonlinearities and take as given the negative economic effects in the linear case.[2] Second, to better model nonlinearities related to economic states, we need a large number of observations and a long sample that includes enough recessions and expansions. The US data we use is available at a monthly frequency since the early 1960s. Applying our econometric model to other economies such as Australia would be more complex due to the shorter period of data availability as well as the low occurrence of recessions and the lack of monthly indicators relevant to our analysis, such as the CPI index.
Following Bloom (2009), the identification of uncertainty shocks pursued in this paper relies on extreme events, that is events associated with large jumps in the level of the S&P 100 Volatility Index (VXO). Such events are related to terror, war, oil and the economy, and are usually bad events; one example is the assassination of John F Kennedy. Thus, our uncertainty shocks can be defined as shocks to the volatility of the US stock market induced by ‘extreme bad events’. These events are likely to be informative as regards unexpected movements in uncertainty that are not associated with the business cycle. Hence, we see these events as valid instruments to overcome the endogeneity problem one faces when searching for exogenous variations in uncertainty. Our results are robust to the employment of the VXO itself as an indicator of uncertainty in our STVAR as well as to the construction of an alternative event dummy based on the financial uncertainty proxy constructed by Ludvigson, Ma and Ng (2015).
Our focus on financial proxies of uncertainty is justified both theoretically and empirically. From a theoretical standpoint, Basu and Bundick (2017) show that movements in a measure of financial uncertainty, which is conceptually in line with the VXO, can be an important driver of the business cycle in a micro-founded macroeconomic model. Empirically, recent findings by Ludvigson et al (2015) and Casarin et al (2016) point to movements in financial uncertainty as possibly exogenous to the business cycle, and able to explain a larger share of the forecast error variance of real activity than movements in real activity indicators of uncertainty.[3]
Are the effects of uncertainty shocks different in good and bad times? We find compelling evidence in favour of a positive answer. Real activity, measured by industrial production and employment, falls much more quickly and sharply when uncertainty shocks hit the economy during recessions. In regards to nominal variables, uncertainty shocks are deflationary, especially in recessions. The response of the policy rate is substantially more marked during economic downturns. Importantly, the difference in the estimated responses in the two states – recessions and expansions – is statistically significant as regards real activity and the policy rate.
Next, we investigate whether the effectiveness of systematic US monetary policy is state-dependent. The term ‘systematic’ here refers to the endogenous movements in the federal funds rate in response to macroeconomic conditions in the aftermath of uncertainty shocks. We run a counterfactual exercise in which systematic policy is assumed not to react to uncertainty as well as to the macroeconomic fluctuations triggered by uncertainty shocks. In other words, we shut down the direct and indirect effects of uncertainty shocks on the federal funds rate. We find a greater effectiveness of policy in tackling uncertainty shocks during expansions. In bad times, the depth of the economic downturn (following an uncertainty shock) remains virtually unchanged, while its persistence is only mildly influenced by the policy rate response to the shock. Differently, in expansions the absence of a systematic policy response would induce a much deeper and longer-lasting downturn after an uncertainty shock. Thus, monetary policy plays an important role in reducing the probability of entering a recession if the uncertainty shock occurs in good times. This is because, in good times, the expansionary policy response mitigates the drop in real activity. But it doesn't help as much if the economy is already in a recessionary state.
Finally, we dig deeper into the systematic relationship between uncertainty and monetary policy in the United States by running a second counterfactual simulation. Specifically, we shut down only the direct effects of uncertainty shocks on the federal funds rate, while allowing monetary policy to respond to all the remaining variables in the system. This is done to understand to what extent the Federal Reserve acted, borrowing the terminology proposed by Greenspan (2004), as a ‘risk manager’ and set the nominal interest rate lower than what it would have set in the absence of uncertainty. The counterfactual policy rate is systematically higher than the historical one in the aftermath of abrupt increases in uncertainty. The gap between the historical federal funds rate and the counterfactual one, which we term ‘risk management-driven policy rate gap’, confirms that risk management was a crucial element of US monetary policy decisions during the period 1962–2008. Importantly, and in line with our previous findings, the risk management-driven policy rate gap tends to be larger in recessions. We show that, absent this risk management policy, we would have observed a lower level of industrial production in the post-WWII period. We corroborate this finding by providing narrative evidence based on our reading of the Federal Open Market Committee (FOMC) minutes released around the uncertainty shocks we identify.
Our evidence on the risk management approach followed by the Federal Reserve is consistent with the results put forth by Evans et al (2015). They estimate several Taylor rules and find evidence in favour of a systematic response of the federal funds rate to a number of uncertainty indicators. In this regard, the key difference between their study and ours is that we run counterfactual simulations conducted with a multivariate nonlinear VAR framework. Our approach allows us to account for second round effects involving the policy rate, uncertainty, and measures of real economic activity.
From a modelling standpoint, our results support the development and use of nonlinear models able to replicate both the contractionary effects and the different economic transmission of uncertainty shocks over the business cycle. Policy wise, our findings offer support for research investigating how to efficiently tackle the state-dependent effects of such shocks.
The paper develops as follows. Section 2 discusses connections with the existing literature. Section 3 presents our nonlinear framework and the data employed in the empirical analysis. Section 4 documents the nonlinear effects of uncertainty shocks and discusses a number of robustness checks. Section 5 analyses the role of systematic monetary policy in recessions and expansions, quantifies to which extent uncertainty systematically affects the policy rate setting, and offers narrative evidence in favour of risk management by the Federal Reserve. Section 6 concludes.
2. Connections with Existing Literature
A recent strand of the literature has dealt with the measurement of uncertainty. Bachmann, Elstner and Sims (2013) use survey data to compute measures of forecast disagreement that proxy time-varying business-level uncertainty for Germany and the United States. Rossi and Sekhposyan (2015, 2017) propose uncertainty indices based on the distribution of real GDP forecast errors. Jurado et al (2015), Ludvigson et al (2015), and Carriero et al (2016) construct measures of uncertainty based on the (un)predictability of several macroeconomic and financial indicators. Baker, Bloom and Davis (2016) develop an index of economic policy uncertainty that reflects the frequency of keywords related to economic concepts, uncertainty, and policy decisions in a set of leading newspapers. Scotti (2016) constructs a proxy for uncertainty based on Bloomberg forecasts that aims to capture agents' uncertainty surrounding current realisations of real economic activity. Our paper focuses on events that are instrumental for the identification of exogenous variations in a financial uncertainty indicator, that is, the VXO.
Our contribution relates to other papers on the relationship between uncertainty and monetary policy. Caggiano, Castelnuovo and Pellegrino (2017) study the effects of uncertainty shocks in normal times and during the zero lower bound period. They find that uncertainty shocks affect real activity more strongly when the bound is binding. With respect to them, we focus on a period during which monetary policy was conventional and investigate the business cycle dependence of the effects of uncertainty shocks on real activity as well as nominal indicators. Hence, our paper is complementary to Caggiano, Castelnuovo and Pellegrino (2017). A related paper is Alessandri and Mumtaz (2014), who investigate the effects of uncertainty shocks in the presence of high/low financial stress. Differently, our conditioning variables are indicators of the business cycle. Moreover, our paper has a focus on the effectiveness of systematic US monetary policy along the business cycle.
A different strand of the literature analyses the effects of monetary policy shocks in recessions and expansions, see, for example, Weise (1999), Mumtaz and Surico (2015), and Tenreyro and Thwaites (2016); or in the presence of high/low uncertainty, as in Aastveit, Natvik and Sola (2013), Eickmeier, Metiu and Prieto (2016), and Pellegrino (2017a, 20017b). Our paper, instead, deals with a set of different questions regarding the impact of uncertainty shocks conditional on a given stance of the business cycle and a given systematic monetary policy conduct. Gnabo and Moccero (2015) find that risks in the inflation outlook and in financial markets are a more powerful driver of monetary policy regime changes in the United States than the level of inflation and the output gap. Our paper complements their study by investigating the ability of systematic monetary policy to stabilise the US macroeconomic environment after an uncertainty shock.
Our findings on the weaker effectiveness of systematic US monetary policy in recessions can be interpreted via a number of theoretical models. In the presence of labour and capital non-convex adjustment costs, Bloom (2009) and Bloom et al (2014) predict a weak impact of changes in factor prices when uncertainty is high due to ‘wait-and-see’ effects. Vavra (2014) and Baley and Blanco (2016) show that higher uncertainty generates higher aggregate price flexibility, which in turn harms the central bank's ability to influence aggregate demand. Berger and Vavra (2015) build up a model featuring microeconomic frictions that lead to a decline in the frequency of households' durable adjustment during recessions. This dampens the response of aggregate durable consumption to macroeconomic shocks, including policy changes. Our findings are also in line with the empirical result put forth by Mumtaz and Surico (2015), who work with a state-dependent IS curve for the United States and estimate a lower interest rate semi-elasticity in recessions.
From a policy standpoint, our results contribute to the discussion on how to respond to uncertainty shocks. Blanchard (2009) proposes to design policies aimed at removing tail risks, channelling funds towards the private sector, and undoing the ‘wait-and-see’ attitudes by creating incentives to spend. Bloom (2014) suggests using more aggressive policies during periods of heightened uncertainty. In the presence of zero nominal rates, Basu and Bundick (2015) find that uncertainty about future shocks may endogenously arise if state-dependent policies, and in particular forward guidance, are not engineered to exit the zero lower bound. Evans et al (2015) and Seneca (2016) argue that it is optimal to delay the lift-off of the policy rate in the presence of uncertainty on future economic conditions. Our evidence on the asymmetric effects of uncertainty shocks and the effectiveness of systematic monetary policy reinforces these calls for state-dependent policy responses.
3. Modelling Nonlinear Effects of Uncertainty Shocks
We estimate the impact of uncertainty shocks on real economic outcomes using a nonlinear VAR model. The vector of endogenous variables Xt includes (from the top to the bottom) the S&P 500 stock market index, an uncertainty dummy based on the VXO, the federal funds rate, a measure of average hourly earnings, the consumer price index, hours worked, employment, and industrial production.[4] These variables are expressed in logs, except the uncertainty dummy, the policy rate, and hours.[5]
We use monthly data covering the period July 1962 to June 2008. We cut the sample in June 2008 to avoid modelling the period that started with the Lehman Brothers bankruptcy and the acceleration of the 2007–09 financial crisis in September 2008. Such acceleration led the Fed to quickly cut the federal funds rate to zero, and maintain the rate at that level until December 2015. We interpret this period as a third regime, the modelling of which would render the estimation of our nonlinear framework more complex.
As in Bloom (2009), the uncertainty dummy takes the value of one when the HP-detrended VXO level rises 1.65 standard deviations above its mean, and zero otherwise.[6] This indicator function is employed to ensure that identification comes from large, and likely to be exogenous, jumps in financial uncertainty that are unlikely to represent systematic reactions to business cycle movements. Given that we base our identification strategy on well-known uncertainty-inducing events, the effects of uncertainty shocks documented in this paper should be seen as responses to extreme jumps in uncertainty rather than a characterisation of the general effects of uncertainty in the economy.[7] In addition, these extreme jumps are largely associated with bad news. This makes our definition of uncertainty shocks slightly different from that commonly used in theoretical studies, that is, uncertainty shocks are usually defined as shocks to the second moment (variance) of the probability density distribution of a given variable. Our identification approach focuses instead on the first moment (shocks to the level) of the VXO. However, in line with the definition of the VXO as being an index of market-implied volatility, we interpret these shocks as shocks to the volatility of the US stock market induced by ‘extreme bad events’. We believe that our dummy-based approach offers a better identification than the usual orthogonalisation of the VAR residuals of the VXO itself. However, identification of causal effects is hard, and our uncertainty shocks may still be picking up endogenous responses that are not captured by our STVAR model.[8]
Figure 1 shows the VXO index along with the NBER recession dates and the identified uncertainty shocks. The sixteen uncertainty-inducing episodes are equally split between recessions and expansions. Noticeably, all recessions are associated with significant spikes in the volatility series. This is in line with a key fact about uncertainty summarised by Bloom (2014), that is, macro uncertainty rises in recessions.
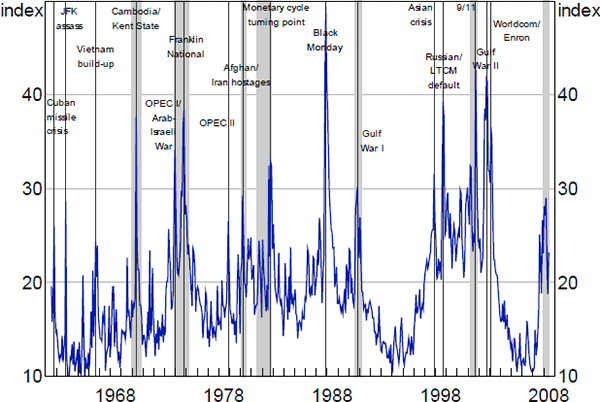
Notes: Chicago Board Options Exchange (CBOE) VXO index of implied volatility on a hypothetical at the money S&P 100 30 days option from 1986 onward; pre-1986 returns' volatilities obtained by computing the monthly standard deviation of the daily S&P 500 index, and normalised to the same mean and variance as the VXO index when they overlap from 1986 onward; the variance is annualised and the index expresses volatility in percentage points; vertical lines denote uncertainty shocks as defined in the paper; shading denotes NBER recessions
Sources: Authors' calculations; Chicago Board Options Exchange; National Bureau of Economic Research
The STVAR model assumes that the vector of endogenous variables can be described as a combination of two linear VARs, one describing the economy in bad times and the other in good times (for a detailed presentation, see Teräsvirta, Tjøstheim and Granger (2010)). In particular, the vector of endogenous variables Xt is modelled with the following STVAR:
In this model, F(zt) is a logistic transition function that captures the probability of being in a recession, γ is the smoothness parameter, zt is a transition indicator, ∏R and ∏E are the VAR coefficients capturing the dynamics of the system in recessions and expansions, εt is the vector of reduced-form residuals with zero mean and time-varying, state-contingent variance-covariance matrix Ωt, where ΩR and ΩE are covariance matrices of the reduced-form residuals estimated during recessions and expansions.
Recent applications of the STVAR model to analyse the US economy include Auerbach and Gorodnichenko (2012), Bachmann and Sims (2012), Berger and Vavra (2014), and Caggiano et al (2015), who employ it to study the effects of fiscal spending shocks in good and bad times, and Caggiano et al (2014) and Caggiano, Castelnuovo and Figueres (2017), who focus on the effects of uncertainty shocks on unemployment in recessions. The key advantage of the STVAR model relative to threshold VARs is that with the latter we may have relatively few observations for recessions, which makes estimates unstable and imprecise. In contrast, estimation and inference for each regime in the STVAR is based on a larger set of observations.[9]
Conditional on the standardised transition variable zt, the logistic function F(zt) indicates the probability of being in a recessionary phase. The transition from one regime to another is regulated by the smoothness parameter γ, that is, large (small) values of γ pimply abrupt (smooth) switches from one regime to another. The linear model à la Bloom (2009) is a special case of the STVAR, obtained when γ = 0; which implies ∏R = ∏E = ∏ and ΩR = ΩE = Ω. We make sure that the residuals of the uncertainty dummy equation are orthogonal to the other residuals of the estimated VAR by imposing a Cholesky decomposition of the covariance matrix of the residuals. Hence, the ordering of the variables admits an immediate response of industrial production and employment, as well as prices and the federal funds rate, to an uncertainty shock. However, these variables do not contemporaneously affect uncertainty. This assumption is consistent with that of exogeneity of the spikes of the VXO identified with the strategy described above. It is also consistent with the theoretical model of Basu and Bundick (2017), in which first-moment or non-uncertainty shocks have almost no effect on financial volatility. We include, however, the S&P 500 index before our uncertainty indicator to control for the impact of the stock market itself on financial volatility.
A key role is played by the transition variable zt (see Equation (4)). Auerbach and Gorodnichenko (2012), Bachmann and Sims (2012), Berger and Vavra (2014), Caggiano et al (2014), and Caggiano et al (2015) use a standardised moving average of the quarterly real GDP growth rate as transition indicator. Our paper deals with monthly data. Similarly to Caggiano, Castelnuovo and Figueres (2017), we employ a standardised backward-looking moving average involving 12 realisations of the month-to-month growth rate of industrial production.[10] Another important choice is the calibration of the smoothness parameter, whose estimation is affected by well-known identification issues (see the discussion in Teräsvirta et al (2010)). We exploit the dating of recessionary phases produced by the National Bureau of Economic Research (NBER) and calibrate γ to match the frequency of the US recessions, which amounts to 14 per cent of our sample. Consistently, we define as ‘recession’ a period in which F(zt) > 0.86, and calibrate γ to obtain Pr(F(zt) > 0.86) ≈ 0.14.[11] This metric implies γ = 1.8. In Appendix B, we show that our results are robust to alternative calibrations of the smoothness parameter γ.
Figure 2 plots the transition function F(zt) for the US post-WWII sample and superimposes the NBER recessions dating. Two observations are in order. First, the transition function peaks with a slight delay relative to the NBER recessions. This is due to our use of a backward-looking transition indicator. This choice enables us to compute the transition probability by using observed values of industrial production, and thus it allows us to account for a switch from one regime to another conditional on the evolution the system after the shock. To put it simply, using a centred moving average would prevent us from calculating GIRFs. Second, the volatility of F(zt) drops when entering the Great Moderation period, that is, 1984–2008. This might suggest the need to re-optimise the calibration of γ to better account for differences in the regime switches occurring in the two sub-samples 1962–83 and 1984–2008. When we do this, the calibration of our smoothness parameter for the two periods reads 1.6 and 1.7 (for capturing the 20 and 8 per cent frequencies of NBER recessions in the two sub-samples).[12] Such calibrations are quite close to the one we employ in our baseline exercise (where γ = 1.8). Estimations conducted with these two alternative values lead to virtually unaltered results (Appendix B). All in all, our transition probability closely tracks the downturns of the US economy.
Since any smooth transition regression model is not identified if the true data generating process is linear, we test the null hypothesis of linearity against the alternative of a logistic STVAR for our vector of endogenous variables. We employ two tests proposed by Teräsvirta and Yang (2014). The first is a LM-type test, which compares the residual sum of squares of the linear model with that of a third-order approximation of the STVAR framework. The second is a rescaled version of the previous test, which accounts for size distortion in small samples. Both test statistics strongly reject the null hypothesis at any conventional significance level. A description of the tests is provided in Appendix A. We also show that the linear impulse responses to an uncertainty shock (calculated with our model when γ = 0) are different from the nonlinear ones (Appendix B).[13]
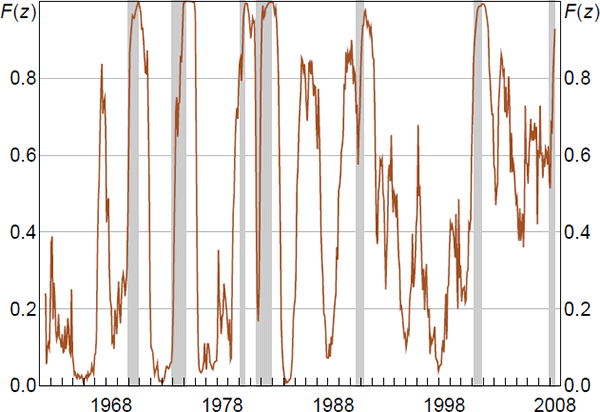
Notes: Transition function F(z) computed by employing the standardised moving average (12 terms) of the month-on-month growth rate of industrial production; shading denotes NBER recessions
We estimate the STVAR model with six lags, a choice supported by standard information criteria as regards the linear version of the VAR model, for which an extensive literature on optimal lag selection in VARs is available. Given the high nonlinearity of the model, we estimate it by employing the Markov Chain Monte Carlo simulation method proposed by Chernozhukov and Hong (2003).[14] The estimated model is then employed to compute GIRFs to an uncertainty shock.[15]
4. Results
Are the real effects of uncertainty shocks state-dependent? Figure 3 plots the estimated dynamic responses of employment and industrial production to an uncertainty shock in recessions and expansions, along with 68 per cent confidence bands. The size of the shock in all scenarios is normalised to induce an on-impact response of uncertainty equal to one. The macro variables react negatively and significantly in both phases of the business cycle. However, the responses are clearly asymmetric. In recessions, the peak short-run response of industrial production is about −2.5 per cent; while that of employment is about −1.5 per cent. The same values in expansions are −1.5 and −0.9 per cent. As shown below, these differences are statistically significant. Hence, we find evidence in favour of an asymmetric response of real activity to uncertainty shocks across the business cycle.[16]
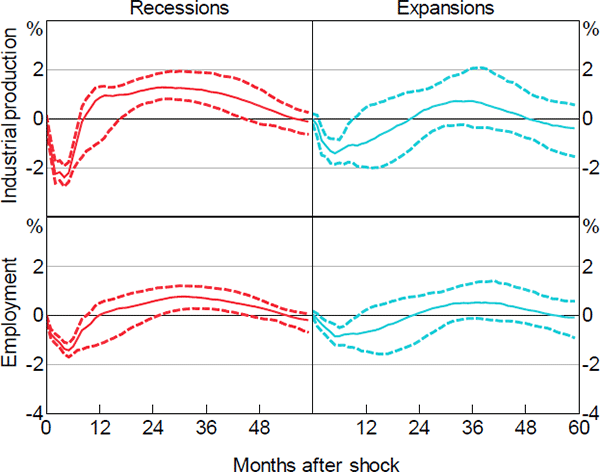
Note: Confidence bands indicate 68 per cent intervals
Our results are in line with recent contributions by Caggiano et al (2014), Nodari (2014), Ferrara and Guérin (2015), Casarin et al (2016), and Caggiano, Castelnuovo and Figueres (2017), who also find that uncertainty shocks have a larger effect on real activity when they occur in recessions. This evidence is robust to a variety of checks, including:
- different identifications of uncertainty shocks based on: a dummy that focuses only on events associated with terror, war, or oil events; the use of the VXO itself; the use of an alternative dummy that identifies extreme events conditional on the one-month ahead financial uncertainty indicator developed by Ludvigson et al (2015)
- different calibrations of the smoothness parameter γ
- the use of unemployment as transition indicator
- the addition of control variables such as credit spreads, house prices, and a long-term interest rate.
In all cases, our results confirm the evidence of asymmetric responses of industrial production and employment (in terms of severity of the recession, speed of the recovery, and overall dynamics). For the sake of brevity, we discuss these robustness exercises in Appendix B.
4.2 Systematic Monetary Policy Response
Next, we analyse the response of systematic monetary policy to macroeconomic uncertainty. To do this, we look at the responses of both prices and the federal funds rate (Figure 4).
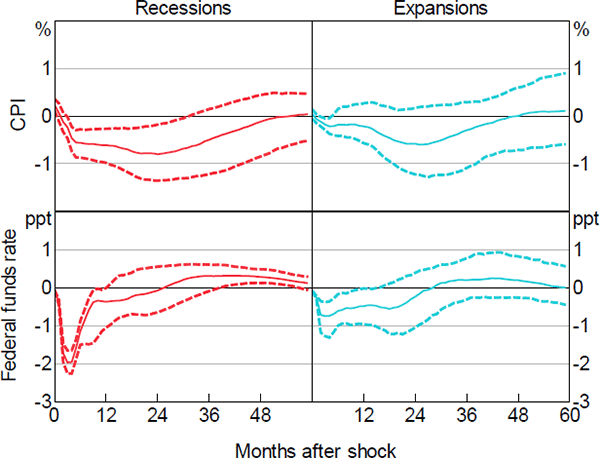
Note: Confidence bands indicate 68 per cent intervals
An uncertainty shock triggers a negative reaction of prices that is statistically significant in recessions only. Prices decrease in the short run and then gradually return to their pre-shock level. The interest rate decreases significantly, both in recessions and expansions. However, the differences between the two states are remarkable in terms of dynamics and quantitative response. When an uncertainty shock hits the economy in good times, the interest rate decreases by about 0.8 percentage points at its peak, and the reaction is short-lived. When an uncertainty shock hits in a recession, the policy rate decreases by about 2 percentage points, and remains statistically below its initial level for a prolonged period of time. These impulse responses support the view put forward by Basu and Bundick (2017) and Leduc and Liu (2016) that uncertainty shocks act as demand shocks.
4.3 Statistical Significance of the Differences
The evidence proposed so far points to differences in the response of real and nominal indicators to an uncertainty shock when quantified in recessions versus expansions. How relevant is this result from a statistical standpoint? Figure 5 plots the differences in the responses of industrial production, employment, prices, and the federal funds rate in recessions versus expansions. Industrial production, employment, and the federal funds rate react significantly stronger to uncertainty shocks in recessions. However, we do not find significant evidence in favour of an asymmetric reaction of prices. Hence, from a statistical standpoint, the more aggressive systematic policy reaction estimated in recessions is likely to be driven by the response of real activity. In the rest of the paper we will focus on the responses of industrial production and employment with the aim of understanding if the effectiveness of the Federal Reserve's systematic policy (in terms of business cycle stabilisation) was different in recessions compared to expansions.
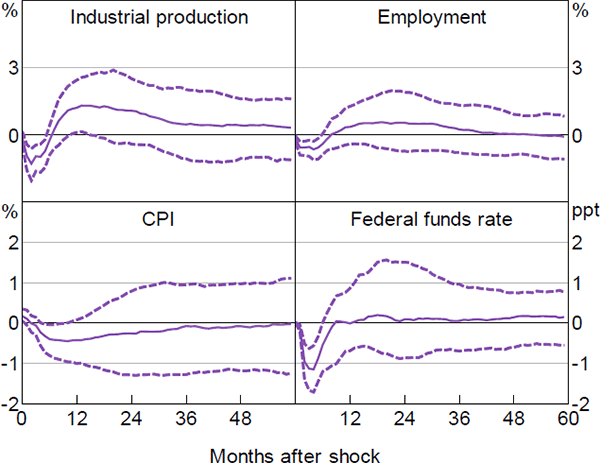
Note: Confidence bands indicate 68 per cent intervals
5. Uncertainty and Monetary Policy
5.1 Systematic Monetary Policy Effectiveness
The previous evidence shows that US monetary authorities react to uncertainty shocks in both phases of the business cycle. But what would have happened if the Federal Reserve had not reacted to the macroeconomic fluctuations induced by uncertainty shocks? Would the recessionary effects of such shocks have been magnified? Answering these questions is key to understanding the role that conventional monetary policy can play in tackling the negative effects triggered by sudden jumps in uncertainty.
To answer these questions, we run a counterfactual simulation using our STVAR. Our counterfactual exercise assumes that the central bank does not respond to an uncertainty shock, that is, we shut down the systematic response of the federal funds rate to movements in the economic system triggered by uncertainty shocks. Following Sims and Zha (2006), we do so by zeroing the coefficients of the federal funds rate equation. Implicitly, in this counterfactual economic agents are repeatedly ‘surprised’ by the failure of monetary policy to respond to the uncertainty shock in its accustomed way, which raises well-known issues highlighted by the Lucas critique. However, for deviations of policy from its historical pattern that are neither too large nor too protracted, our estimates of the policy effects provide reasonable counterfactual approximations (Sims and Zha 2006).
Figure 6 compares the reaction of real activity conditional on the absence of a systematic monetary policy response to the baseline results. The results suggest that the effectiveness of systematic monetary policy is lower in recessions. In other words, the recession is estimated to be as severe as the one that occurs when we allow policymakers to lower the policy rate. Notably, the difference between the baseline and the counterfactual scenarios mainly regards the speed with which real activity recovers and overshoots before going back to the steady state. Possibly this is due to the lags via which monetary policy affects the real economy.
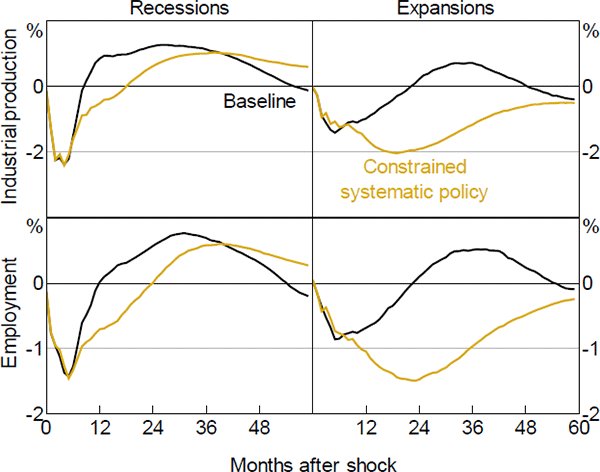
A different picture emerges in good times. As Figure 6 shows, when the policy rate is kept fixed, industrial production goes down markedly (about 2 per cent at its peak) and persistently, remaining statistically below zero for a prolonged period of time.[17] The same holds when looking at the response of employment, that is, the gap between the baseline response and the one associated with our counterfactual scenario is quantitatively substantial in expansions. This suggests that monetary policy plays an important role in reducing the probability of entering a recession if the uncertainty shock occurs in good times. But it doesn't make much difference if the economy is already in a recessionary state.
5.2 Interpreting Policy (In)effectiveness in Recessions
How can one interpret the state-dependence of monetary policy effectiveness? As suggested by Bloom (2009) and Bloom et al (2014), these findings might find a rationale in the real option value theory. When uncertainty is high, firms' inaction region expands as the real option value of waiting for new information increases (Bloom 2009). In recessions, it could be that the ‘wait-and-see’ behaviour becomes optimal for a larger number of firms compared to normal times. If the real option value of waiting is high, firms become insensitive to changes in the interest rate, which explains why the peak recessionary effect is virtually identical regardless of the reaction of monetary policy. When uncertainty starts to drop, the inaction region shrinks, firms become more willing to invest and face their pent-up demand. In turn, the elasticity of investment with respect to the interest rate starts increasing. If monetary policy does not react, as in our counterfactual scenario, the higher (relative to the baseline) cost of borrowing starts playing a role. Hence, firms re-start investing at a slower pace. In the medium run, once uncertainty has vanished, firms invest less with respect to the baseline case, and the overshoot is substantially milder, if at all. A similar reasoning applies to labour demand and, therefore, employment.
Differently, the response of monetary policy has a larger countercyclical effect on the downturn triggered by uncertainty shocks in expansions. If the option value of waiting due to uncertainty is lower in expansions compared to recessions, firms are more reactive to changes in factor prices. Hence, if the nominal interest rate remains unchanged, investment is likely to be lower. Consequently, uncertainty shocks trigger stronger contractionary effects in absence of systematic monetary policy interventions.
These findings line up with those in Vavra (2014), who shows that monetary policy shocks are less effective during periods of high volatility. In his model, despite the presence of an inaction region due to price adjustment costs, second moment shocks push firms to adjust their prices more often. This increased price dispersion translates into higher aggregate price flexibility, which dampens the real effects of monetary policy shocks. Given the countercyclicality of price volatility, monetary policy turns out to be less powerful in recessions. A similar mechanism is present in Baley and Blanco (2016). Our results complement Vavra's and Baley and Blanco's, because we show that the systematic component of monetary policy is less effective in recessions.
Berger and Vavra (2015) build up partial and general equilibrium models that focus on the response of aggregate durable expenditures to a variety of macroeconomic shocks. In particular, their model features microeconomic frictions that lead to a decline in the frequency of households' durable adjustment during recessions. This decline in the probability of adjusting during recessions, in conjunction with the variation over time in the distribution of households' durable holdings, implies a procyclical impulse response of aggregate durable spending to macroeconomic shocks, a result also documented in Berger and Vavra (2014). Hence, macroeconomic policies are less effective in stabilising the business cycle (at least, durable spending) in recessions, consistent with our counterfactual impulse responses.
Our empirical findings are also consistent with those by Weise (1999), Aastveit et al (2013), Mumtaz and Surico (2015), Tenreyro and Thwaites (2016), Eickmeier et al (2016), and Pellegrino (2017a, 2017b), who also find monetary policy to be less powerful in periods of high uncertainty or, more generally, during recessions. In particular, Mumtaz and Surico (2015) use quantile regression techniques to estimate a nonlinear empirical model of consumption, in which the conditional quantile distribution of consumption is a function of the real interest rate and leads and lags of consumption itself. They show that, when real activity is above average, the degree of forward-lookingness and the interest rate semi-elasticity are significantly larger than the values estimated when real activity is below average. This implies that, all else being equal, monetary policy is more powerful in good than in bad times. Given the tight link between the IS schedule (which refers to the consumption/saving decisions by households) and the financial markets, our results might also be seen as consistent with the different role played by financial frictions in economic booms and busts.
We note that, as is the case for any given counterfactual simulation, the accuracy of our results on the effectiveness of systematic monetary policy depends on all else being equal. Our counterfactual is a ceteris paribus exercise in that the only difference between our baseline results and the ones obtained with the counterfactual simulation is the response of the federal funds rate to the uncertainty shock. However, we cannot rule out the possibility that the nonlinear effects of systematic monetary policy uncovered in our analysis are also capturing nonlinearities related to other macroeconomic policies, most notably fiscal policy.[18]
5.3 Risk Management by the Federal Reserve
The evidence provided so far shows that uncertainty shocks trigger a response by monetary policymakers, and that this response is particularly strong during recessions. But what role did uncertainty per se play as far as the US monetary policy setting is concerned? In analysing the conduct of monetary policy under his regime, Greenspan (2004, pp 36–37) states that:
The Federal Reserve's experiences over the past two decades make it clear that uncertainty is not just a pervasive feature of the monetary policy landscape; it is the defining characteristic of that landscape … the conduct of monetary policy in the United States has become to involve, at its core, crucial elements of risk management.
While being consistent with Greenspan's statement, the impulse response analysis documented in Section 4 does not necessarily point to a systematic monetary policy reaction to uncertainty directly. Second round effects, working through the impact that uncertainty shocks exerted on real activity and prices in our sample, represent an alternative, not mutually exclusive, potential explanation for the response of the policy rate. It is then of interest to shed further light on whether the Federal Reserve reacted directly to movements in uncertainty, acting as a ‘risk manager’, or rather it simply reacted to movements in real activity and prices induced by uncertainty shocks.
To isolate the direct systematic response of the Federal Reserve to variations in uncertainty, we proceed in two ways. First, we run a counterfactual simulation to produce the ‘risk management-driven policy rate gap’. This gap is constructed by computing the difference between the realised (i.e. historical) federal funds rate and the counterfactual policy rate that, according to our nonlinear VAR, we would have observed if the Federal Reserve had not systematically reacted to uncertainty in our sample. Specifically, we construct the counterfactual policy rate by only zeroing the coefficients on the uncertainty variable in the federal funds rate equation, and calculating its fitted values accordingly.[19] Evidence of a negative gap would point to a higher interest rate in absence of a systematic policy response to uncertainty. Hence, it would be consistent with the claim that the Federal Reserve acted as a ‘risk manager’. Second, we analyse the minutes of the FOMC meetings to see whether there is narrative evidence in favour of risk management.
5.3.1 Empirical evidence
Figure 7 plots the difference between the historical and the counterfactual federal funds rate. Given that we consider all shocks hitting the economic system, the baseline scenario (the one that allows for the estimated systematic response of the federal funds rate to contemporaneous and past realisations of uncertainty) replicates the historical realisations of the federal funds rate. Two observations are in order. First, after the realisation of an uncertainty shock, the contemporaneous difference between the historical rate and the counterfactual one turns out to be negative. This suggests that, in absence of a systematic monetary policy response to uncertainty, the federal funds rate would have been higher in the aftermath of spikes in uncertainty. Second, the gap between the historical and the counterfactual policy rates widens in recessions by −47 basis points on average.
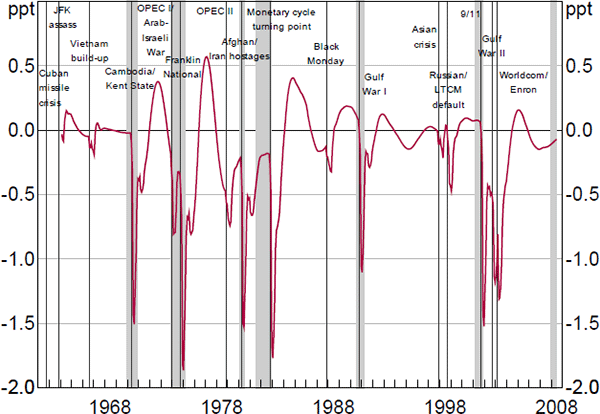
Notes: Difference between the historical federal funds rate and the counterfactual rate computed by constraining the response of the policy rate to current and past realisations of uncertainty; vertical lines denote uncertainty shocks as defined in the paper; shading denotes NBER recessions
Our counterfactual exercise also points to a non-negligible positive effect of this risk management approach on industrial production. As documented in Table 1, the average deviation of the historical realisations of industrial production from the ‘no risk management’ path over the entire sample is 0.66 per cent. In other words, if the Federal Reserve did not consider macro uncertainty when setting monetary policy, the level of industrial production would have been lower. Looking at differences across the business cycle, this gap would have been larger in expansions. The indication of a lower push for industrial production by systematic monetary policy in recessions is in line with our previous finding that systematic monetary policy is less effective during economic downturns.
| Full sample | Recessions | Expansions | |
|---|---|---|---|
| Federal funds rate | −0.16 | −0.47 | −0.11 |
| Industrial production | 0.66 | 0.50 | 0.69 |
| Inflation | 0 | −0.06 | 0.01 |
| Employment | −0.02 | −0.17 | −0.07 |
|
Notes: Sample covers 1964:M2–2008:M6; gaps constructed by taking the difference between the historical realisations of each variable and their counterfactual values obtained by inhibiting the systematic response of the policy rate to current and past realisations of uncertainty in our VAR; federal funds rate is the difference expressed in basis points; other variables are percentage point differences computed as log deviations of the historical realisations from the counterfactual realisations, no risk management values; realisations of the counterfactual rate start in 1964:M2 because of initial conditions (lags of the VAR, transition indicator of the logistic function) |
|||
Differently, not much change would have emerged on average as regards employment and inflation. These macroeconomic aggregates would have followed a similar historical path regardless of risk management. Thus, the lower level of industrial production that we would have observed if the Federal Reserve did not act as a risk manager (i.e. if it did not keep interest rates low in response to heightened uncertainty) would likely be, in part, a result of lower capital stock in the economy.[20]
5.3.2 Narrative evidence
Our empirical analysis assigns a role to uncertainty as a driver of US monetary policy decisions. We link this empirical evidence to the narrative evidence that emerges from the reading of the FOMC minutes. Specifically, we collect excerpts from the FOMC minutes (released around our uncertainty shock dates) with references to uncertainty, risk, and risk management (see Table C1). The reading of the FOMC minutes confirms that uncertainty was an element carefully considered by the members of the FOMC when deciding over the federal funds rate setting. We highlight some of the most informative examples below.
Uncertainties related to external events like the first oil crisis and the Arab-Israeli called for cautious behaviour at the end of 1973:
… in light of current uncertainties regarding the economic outlook and the sensitive state of financial market psychology, current money market conditions be maintained for the time being.
Black Monday is a textbook example of an uncertainty-inducing event. In October 1987, the minutes report that:
The Committee recognizes that still sensitive conditions in financial markets and uncertainties in the economic outlook may continue to call for a special degree of flexibility in open market operations.
The risk management approach by the Federal Reserve appears evident also during the Asian crisis, as the reading of the December 1997 minutes suggests:
While developments in Southeast Asia were not expected to have much effect on the U.S. economy, global financial markets had not yet settled down and further adverse developments could have greater-than-anticipated spillover effects on the ongoing expansion. In this environment, with markets still skittish, a tightening of U.S. monetary policy risked an oversized reaction … At the conclusion of the Committee's discussion, all but one member supported a directive that called for maintaining conditions in reserve markets that were consistent with an unchanged federal funds rate of about 5-1/2 percent and that retained a bias toward the possible firming of reserve conditions and a higher federal funds rate during the intermeeting period.
Another example is the Gulf War II. It created a high degree of uncertainty about future domestic economic outcomes, as suggested by the March 2003 minutes:
… members commented that an unusually high degree of uncertainty had made it very difficult to assess the factors underlying the performance of the economy … In light of these considerable uncertainties, the members agreed that heightened surveillance of evolving economic trends would be especially useful in the weeks ahead … the Committee in the immediate future seeks conditions in reserve markets consistent with maintaining the federal funds rate at an average of around 1-1/4 percent.
Wrapping up, both our econometric results and the narrative evidence based on the FOMC minutes point to a risk management approach by the Federal Reserve. In periods of expectations of sustained future growth and inflationary pressures surrounded by high uncertainty, this risk management practice translated into a ‘wait-and-see’ behaviour, that is, increases in the policy rate to tackle nascent inflation were postponed (e.g. the response to the 1997 uncertainty shock related to the Asian crisis). Differently, expectations of a gloomy economic scenario in a high uncertainty environment led the Federal Reserve to implement larger decreases of the policy rate than those that would have been implemented in absence of uncertainty (e.g. the decisions taken after the 1990 first Gulf War shock and after the 9/11 attacks).[21]
Evans et al (2015) also identify excerpts of the FOMC minutes that discuss uncertainty triggered by national and international factors. They assess the statistical and economic relevance of risk management by the US monetary policymakers by constructing judgemental and automatic (keyword-based) indicators using the minutes of the FOMC meetings as a database. They then use these indicators, along with a number of other proxies for uncertainty, to estimate augmented Taylor rules in which these measures of uncertainty are included one at a time on top of inflation and output. Evans et al (2015) find evidence pointing to a significant and negative contemporaneous response of the Federal Reserve to uncertainty in the period 1987–2008. Hence, their evidence suggests that the Federal Reserve adopted a looser policy in the presence of uncertainty. Our analysis and narrative-based investigation point to the same qualitative conclusion.[22]
6. Conclusion
This paper quantifies the effects of uncertainty shocks in good and bad times and investigates the role that US monetary policy plays in tackling such shocks. Using a nonlinear VAR model, we show that the contractionary effects of uncertainty shocks are stronger when they hit the economy during recessions compared to expansionary times.
Counterfactual simulations, conducted to assess the role of systematic monetary policy, point to policy ineffectiveness in the short run. Policy effectiveness increases in the medium run, especially in good times. In particular, monetary policy plays an important role in reducing the probability of entering a recession if the uncertainty shock occurs during an expansion. This is because expansionary systematic policy mitigates the drop in real economic activity caused by the uncertainty shock. However, the policy response doesn't help as much if the economy is already in a recessionary state. These empirical findings lend support for theoretical models like those developed by Vavra (2014), Berger and Vavra (2015), and Baley and Blanco (2016), which predict a reduced ability of monetary policymakers to influence output in the presence of high uncertainty.
We also provide empirical and narrative evidence of a risk management-approach adopted by the Federal Reserve during the period we analyse. Economic uncertainty affected the decisions taken by the Federal Open Market Committee, which acted as a risk manager hedging against downside risks. This led US policymakers to keep the federal funds rate lower than that suggested by changes in inflation and output. Our evidence, based on counterfactual simulations conducted within a multivariate nonlinear VAR model, lines up with that proposed by Evans et al (2015) and Seneca (2016), who work with augmented Taylor rules. We corroborate our results by narrative evidence coming from the minutes of the FOMC meetings.
Overall, our findings support a research agenda aimed at identifying state-dependent frictions that can generate different dynamic responses to structural shocks in recessions and expansions. In terms of stabilisation policies, high uncertainty reduces the sensitivity of output to stimulus interventions, above all in recessions. Our findings call for the design of state-dependent policy responses, possibly closer to first moment policies in expansions, but clearly different from them in recessions. Blanchard (2009) and Bloom (2014) call for larger policy stimuli in bad times, as well as second moment policies like stabilisation packages designed to reduce systemic risk. Baker et al (2016) point to the role of clear policy communication and steady policy implementation. Basu and Bundick (2015) find that, in economies characterised by a binding zero lower bound, the inability of the central bank to tackle adverse shocks may contribute to increasing uncertainty about future shocks, and lead to severe contractions. They advocate the use of state-dependent policies, and in particular forward guidance, to exit the zero lower bound. Evans et al (2015) and Seneca (2016) show that it is optimal to hold the policy rate lower than otherwise when expectations of improving future economic conditions are surrounded by uncertainty. Our results suggest that state-dependent policy prescriptions like these should be carefully assessed in order to exit phases characterised by severe economic conditions in the presence of high uncertainty.
Appendix A: Technical Details
This appendix documents statistical evidence in favour of a nonlinear relationship between the endogenous variables included in our STVAR. It also provides details on the estimation procedure of our nonlinear VARs, and on the computation of the GIRFs.
A.1 Statistical Evidence in Favour of Nonlinearities
To detect nonlinear dynamics at a multivariate level, we apply the test proposed by Teräsvirta and Yang (2014). Their framework is particularly well suited for our analysis since it proposes testing the null hypothesis of linearity versus a specified nonlinear alternative, that of a STVAR with a single transition variable.
Consider the following p-dimensional 2-regime approximate logistic STVAR model:
where Xt is the (p × 1) vector of endogenous variables, Yt = [Xt − 1|…|Xt − k|∝] is the ((k × p + q) × 1) vector of exogenous variables (including endogenous variables lagged k times and a column vector of constants ∝), zt is the transition variable, and Θ0 and Θi are matrices of parameters. In our case, the number of endogenous variables is p = 8, the number of exogenous variables is q = 1, and the number of lags is k = 6. Under the null hypothesis of linearity, Θi = 0 ∀i.
The Teräsvirta-Yang test for linearity versus the STVAR model can be performed as follows:
- Estimate the restricted model (Θi = 0 ∀i) by regressing Xt on Yt. Collect the residuals E and compute the matrix of residual sum of squares RSS0 = E’E.
-
Run an auxiliary regression of E on (Yt,Zn)
where
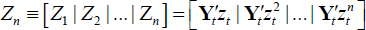 . Collect the
residuals Ξ and compute the matrix residual sum of squares RSS1 = Ξ’Ξ.
. Collect the
residuals Ξ and compute the matrix residual sum of squares RSS1 = Ξ’Ξ.
-
Compute the test statistic
Under the null hypothesis, the test statistic is distributed as a χ2 with p(kp + q) degrees of freedom. For our model, we get a value of LM = 1992 with a corresponding p-value equal to zero. The LM statistic has been computed by fixing the value of the order of the Taylor expansion n = 3, as suggested by Luukkonen, Saikkonen and Teräsvirta (1988). We note, however, that the null of linearity can be rejected also for n = 2. - As pointed out by Teräsvirta and Yang (2014), however, in small samples the LM-type test might suffer from positive size distortion, that is, the empirical size of the test exceeds the true asymptotic size. We then also employ the following rescaled LM test statistic: where G is the number of restrictions. The rescaled test statistic follows an F(G,pT − k) distribution. In our case, we get F = 13.54, with a p-value approximately equal to zero.
A.2 Estimation of the Nonlinear VARs
Our model (1)–(4) is estimated via maximum likelihood.[23] Its log-likelihood reads as follows:
where 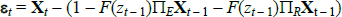 is the vector of
residuals. Our goal is to estimate the parameters
is the vector of
residuals. Our goal is to estimate the parameters 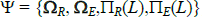 ,
,
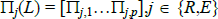 . We do so by
conditioning on a given value for the smoothness parameter γ, which is calibrated as described in the
text. The high nonlinearity of the model and its many parameters make its estimation with standard optimisation
routines problematic. Following Auerbach and Gorodnichenko (2012), we employ the procedure described below.
. We do so by
conditioning on a given value for the smoothness parameter γ, which is calibrated as described in the
text. The high nonlinearity of the model and its many parameters make its estimation with standard optimisation
routines problematic. Following Auerbach and Gorodnichenko (2012), we employ the procedure described below.
Conditional on {γ,ΩR,ΩE}, the model is linear in {∏R(L),∏E(L)}.
Then for a given guess on {γ,ΩR,ΩE}, the
coefficients {∏R(L),∏E(L)} can be estimated by
minimising 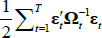 . This can
be seen by re-writing the regressors as follows. Let:
. This can
be seen by re-writing the regressors as follows. Let:
be the extended vector of regressors, and ∏ =
[∏R(L),∏E(L)]. Then, we can write 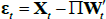 . Consequently, the
objective function becomes:
. Consequently, the
objective function becomes:
It can be shown that the first-order condition with respect to ∏ is:
This procedure iterates over different sets of values for {ΩR, ΩE}, conditional on a given value for γ. For each set of values, ∏ is obtained and the log L computed.
Given that the model is highly nonlinear in its parameters, several local optima might be present. Hence, it is
recommended to try different starting values for {ΩR, ΩE} and then
explore the robustness of the estimates to different values of γ. To ensure positive definiteness of
the variance-covariance matrices, we focus on the alternative vector of parameters 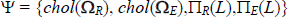 , where chol
implements a Cholesky decomposition.
, where chol
implements a Cholesky decomposition.
The construction of confidence intervals for the parameter estimates is complicated by the nonlinear structure of the problem. We compute them by appealing to a Markov Chain Monte Carlo (MCMC) algorithm developed by Chernozhukov and Hong (2003) (CH hereafter). This method delivers both a global optimum and densities for the parameter estimates.
CH estimation is implemented via a Metropolis-Hastings algorithm. Given a starting value Ψ(0), the procedure constructs chains of length N of the parameters of our model following these steps:
Step 1. Draw a candidate vector of parameter values Θ(n) = Ψ(n) + ψ(n) for the chain's n + 1 state, where Ψ(n) is the current state and Ψ(n) is the vector of iid shocks drawn from N(0,Ωψ), and Ωψ is a diagonal matrix.
Step 2. Set the n + 1 state of the chain Ψ(n + 1) =
Θ(n) with probability 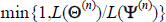 where L(Θ(n)) is the value of the likelihood function conditional on the candidate
vector of parameter values, and L(Ψ(n)) the value of the likelihood function
conditional on the current state of the chain. Otherwise, set Ψ(n + 1) =
Ψ(n).
where L(Θ(n)) is the value of the likelihood function conditional on the candidate
vector of parameter values, and L(Ψ(n)) the value of the likelihood function
conditional on the current state of the chain. Otherwise, set Ψ(n + 1) =
Ψ(n).
The starting value Θ(0) is computed by working with a second-order Taylor approximation of the model
(1)–(4) (see the main text), so that the model can be written as regressing Xt
on lags of Xt,
Xtzt and 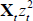 . The
residuals from this regression are employed to fit the expression for the reduced-form time-varying
variance-covariance matrix of the VAR using maximum likelihood to estimate ΩR and
ΩE. Conditional on these estimates and given a calibration for γ, we can
construct Ωt. Conditional on Ωt, we can get starting values for
∏R(L) and ∏E(L).
. The
residuals from this regression are employed to fit the expression for the reduced-form time-varying
variance-covariance matrix of the VAR using maximum likelihood to estimate ΩR and
ΩE. Conditional on these estimates and given a calibration for γ, we can
construct Ωt. Conditional on Ωt, we can get starting values for
∏R(L) and ∏E(L).
Given a calibration for the initial (diagonal matrix) ΩΨ, a scale factor is adjusted to generate an acceptance rate close to 0.3, a typical choice for this kind of simulation (Canova 2007). We employ N 50,000 draws for our estimates, and retain the last 20 per cent for inference. Checks performed with N = 200,000 draws delivered very similar results.
As shown by CH, 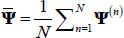 is a
consistent estimate of Ψ under regularity assumptions on maximum likelihood estimators. Moreover, the
covariance matrix of Ψ is given by
is a
consistent estimate of Ψ under regularity assumptions on maximum likelihood estimators. Moreover, the
covariance matrix of Ψ is given by 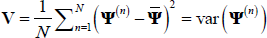 , that is the variance of the estimates in the
generated chain.
, that is the variance of the estimates in the
generated chain.
A.3 Generalised Impulse Response Functions
We compute the generalised impulse response functions from our STVAR model by following the approach proposed by Koop et al (1996). The algorithm features the following steps.
- Consider the entire available observations, with sample size t = 1962:M7,…, 2008:M6, with T = 552, and construct the set of all possible histories Λ of length p = 12:{λi ∈ Λ}. Λ will contain T − p + 1 histories λi.[24]
-
Separate the set of all recessionary histories from that of all expansionary histories. For each
λi calculate the transition variable
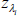 . If
. If 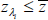 = −1.01 per
cent, then λi ∈ ΛR, where
ΛR is the set of all recessionary histories. If
= −1.01 per
cent, then λi ∈ ΛR, where
ΛR is the set of all recessionary histories. If 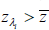 =
−1.01 per cent, then λi ∈ ΛE, where
ΛE is the set of all expansionary histories.
=
−1.01 per cent, then λi ∈ ΛE, where
ΛE is the set of all expansionary histories.
-
Select at random one history λi ∈ ΛR. For the
selected history, take
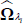 obtained as:
where
obtained as:
where 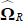 and
and 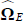 are obtained from
the generated MCMC chain of parameter values during the estimation phase.[25]
are obtained from
the generated MCMC chain of parameter values during the estimation phase.[25] 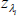 is the
transition variable calculated for the selected history λi.
is the
transition variable calculated for the selected history λi.
-
Cholesky-decompose the estimated variance-covariance matrix
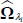 :
and orthogonalise the estimated residuals to get the structural shocks:
:
and orthogonalise the estimated residuals to get the structural shocks:
-
From
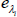 draw with
replacement h eight-dimensional shocks and get the vector of bootstrapped shocks
where h is the horizon for the IRFs we are interested in.
draw with
replacement h eight-dimensional shocks and get the vector of bootstrapped shocks
where h is the horizon for the IRFs we are interested in.
-
Form another set of bootstrapped shocks that will be equal to Equation (A1) except for the
kth shock in
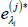 , which is the shock we want to perturb by an
amount equal to δ. Denote the vector of bootstrapped perturbed shocks by
, which is the shock we want to perturb by an
amount equal to δ. Denote the vector of bootstrapped perturbed shocks by 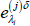 .
.
-
Transform back
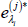 and
and 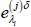 as follows:
and
as follows:
and
-
Use Equations (A2) and (A3) to simulate the evolution of
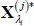 and
and 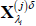 and construct
GIRF(j)(h, δ, λi) as
and construct
GIRF(j)(h, δ, λi) as 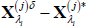 .
.
- Conditional on history λi, repeat for j = 1,…,B vectors of bootstrapped residuals and get GIRF(1) (h, δ, λi), GIRF(2) (h, δ, λi),…,GIRF(B) (h, δ, λi). Set B = 500.
- Calculate the GIRF conditional on history λi as:
-
Repeat all previous steps for i = 1,…, 500 histories belonging to the set of recessionary
histories,
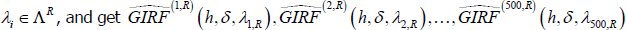 .
.
-
Take the average and get
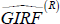 (h, δ,
ΛR), which is the average GIRF under recessions.
(h, δ,
ΛR), which is the average GIRF under recessions.
-
Repeat steps 3 to 12 for 500 histories belonging to the set of all expansions and get
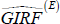 (h, δ, ΛE).
(h, δ, ΛE).
-
The computation of the 68 per cent confidence bands for our impulse responses is undertaken by picking up, per
each horizon of each state, the 16th and the 84th percentile of the densities
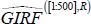 and
and
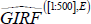 .
.
Appendix B: Robustness Analysis
B.1 Identification of Uncertainty Shocks
We test the robustness of our results to three different uncertainty proxies. First, we construct an uncertainty dummy by considering just 10 out of 16 extreme realisations of the VXO, that is, those that are associated to terror, war, or oil events.[26] Second, we identify an uncertainty shock as an unpredictable movement of the VXO itself, obtained via a Cholesky decomposition of the variance-covariance matrix of the estimated VAR residuals. In this exercise, the VXO replaces the uncertainty dummy in the vector of variables we model. Third, we compute an ‘extreme event dummy’ by following the same identification strategy presented in Section 2, but considering the one-month ahead financial uncertainty indicator recently developed by Ludvigson et al (2015). Figure B1 plots the impulse responses of industrial production and employment conditional on these alternative indicators of uncertainty, and contrasts such responses with the baseline results, which turn out to be robust.
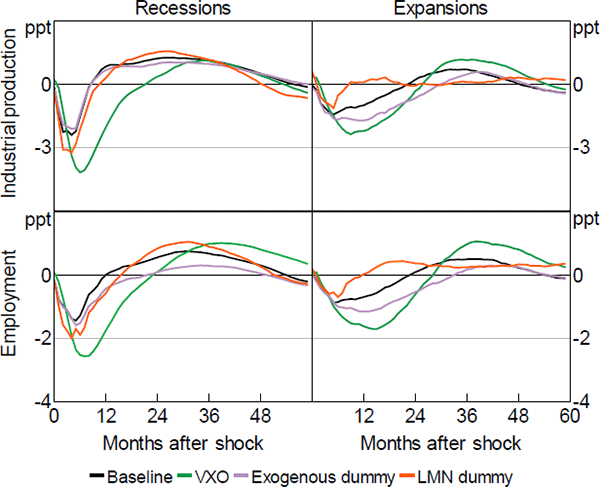
Notes: ‘Baseline’ is the uncertainty dummy as described in the paper; ‘VXO’ is the uncertainty shock identified as the orthogonalised residual of the of the VXO in the VAR; ‘Exogenous dummy’ is the uncertainty dummy constructed by considering extreme realisations of the VXO index related to terror, war and oil events only; ‘LMN dummy’ is the uncertainty dummy constructed by considering extreme events as defined in the paper and associated to the financial uncertainty indicator à la Ludvigson, Ma and Ng (2015)
B.2 Different Calibrations of the Smoothness Parameter
One potential drawback of our empirical exercise is that the smoothness parameter γ of the logistic function of our STVAR, which drives the smoothness with which the economy switches from one regime to another, is calibrated. Our baseline estimation uses a value of γ = 1.8, selected so that the economy spends 14 per cent of the time in recessions (the frequency observed in our sample according to the NBER definition of recessions). To ensure that our results are robust to different values of γ, we re-estimate the model using values of between 1.4 and 2.2, which imply a frequency of recessions in the sample equal to 10 and 25 per cent, respectively. Following Hansen (1999), we set to 10 per cent the frequency corresponding to the minimum amount of observations each regime should contain to be identified. Figure B2 shows the results of this robustness check.
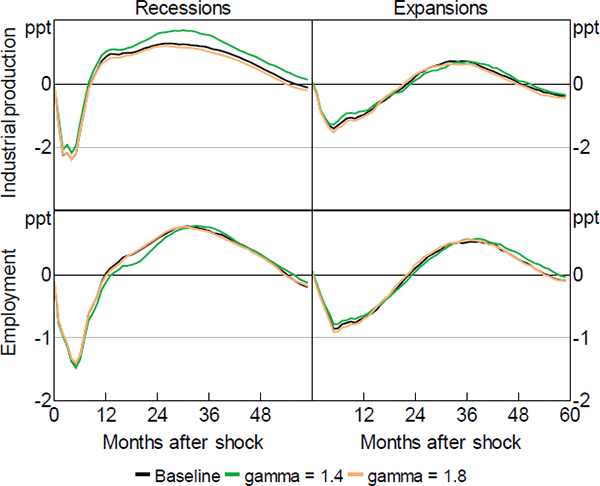
B.3 Unemployment as Transition Indicator
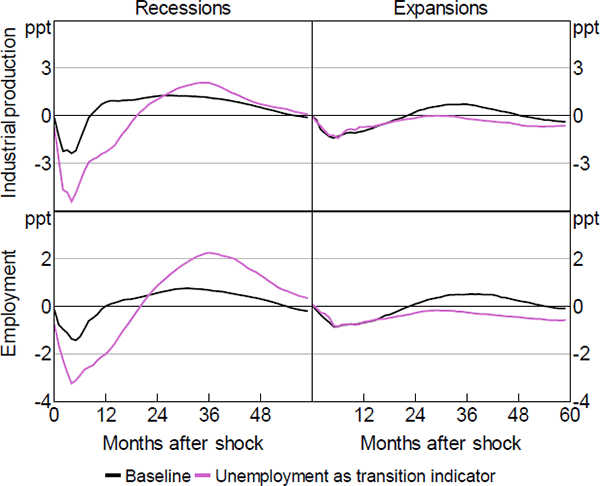
In our baseline exercise, we use industrial production as our transition indicator z. An alternative indicator of the business cycle often considered by policymakers and academics is the unemployment rate. We check the robustness of our results by using the unemployment rate as the transition indicator. Following Ramey and Zubairy (forthcoming), we classify periods in which the unemployment rate is over (under) 6.5 per cent as recessionary (expansionary). We calibrate the smoothness parameter γ = 1.7 to match the 14 per cent frequency of recessions in the sample, as classified by the NBER. Figure B3 documents our GIRFs, which deliver the same stylised facts as in our baseline analysis.
B.4 Uncertainty and Financial Risk
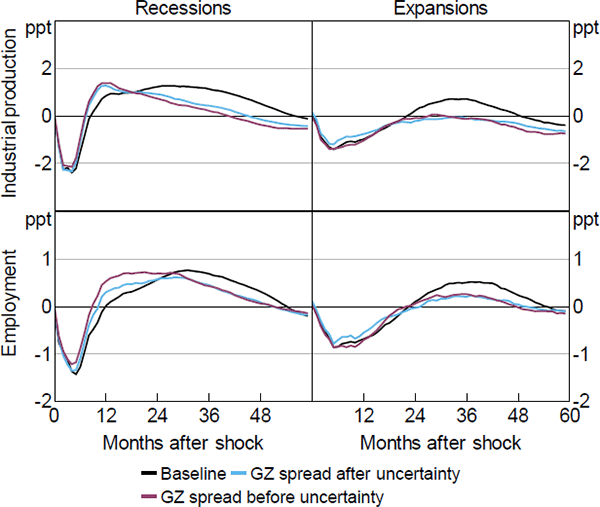
Stock and Watson (2012) point out that financial strains lead to higher uncertainty, which in turn increases financial risk. An implication of this relationship for our analysis is that the transmission of uncertainty shocks may be driven by the level of financial stress in the economy. Caldara et al (2016) provide empirical evidence in favour of larger real effects of uncertainty shocks in periods of high financial stress. A way to control for the presence of time-varying financial risk is by including a measure of credit spread in our VAR. Gilchrist and Zakrajšek (2012) constructed a credit spread cleaned by the systematic movements in default risk of individual firms, the GZ spread. This measure has the attractive feature of isolating the cyclical changes in the relationship between measured default risk and credit spreads. The GZ spread is available from 1973. Our baseline analysis starts in 1962. So we regress the GZ spread against the difference between i) the AAA corporate bonds and the 10-year Treasury yield; ii) the BAA corporate bonds and the 10-year Treasury yield; iii) the 6-month Treasury bill rate and the 3-month Treasury bill rate; iv) the 1-year Treasury yield and the 3-month Treasury bill rate; v) the 10-year Treasury yield and the 3-month Treasury bill rate. We do this for the sample 1973–2008, and then we use the fitted values of the regression to backcast the GZ spread and match our baseline sample. All data are taken from the Federal Reserve Bank of St. Louis' FRED database. We then add this measure of credit spread to our baseline model.
Figure B4 reports the results of this robustness check. We consider two alternative Cholesky orderings to identify uncertainty shocks. First, the credit spread is ordered before uncertainty, implying that uncertainty responds contemporaneously to credit spread but not vice versa. Second, the credit spread is ordered after uncertainty, so to admit a contemporaneous reaction of credit spread to changes in uncertainty. Our results broadly confirm those of our baseline scenario, and are consistent with the findings by Bekaert et al (2013), which show that uncertainty shocks induce business cycle fluctuations even when controlling for indicators of time-varying risk aversion. Our results are also consistent with those in Caldara et al (2016), who show that uncertainty shocks working via credit frictions may lead to a persistent decline in real and financial variables.
B.5 Uncertainty and Housing
Furlanetto et al (2014) show that uncertainty shocks may play a minor role if one controls for housing shocks. To ensure that our results are not driven by dynamics in the housing market, we add the real home price index computed by Robert Shiller to our baseline model.[27] As before, we consider two alternative orderings and place house prices before and after uncertainty. Figure B5 shows the results of this check. Quite interestingly, the presence of house prices does not appear to affect the drop and rebound of industrial production and employment in bad times. However, it clearly dampens their overshoot in the medium run. In expansions, house prices moderate the response of real activity also in the short run, consistent with Furlanetto et al (2014). However, even when controlling for house prices, we find asymmetric responses of industrial production and employment (in terms of severity of the recession, speed of the recovery, and overall dynamics) over the business cycle.
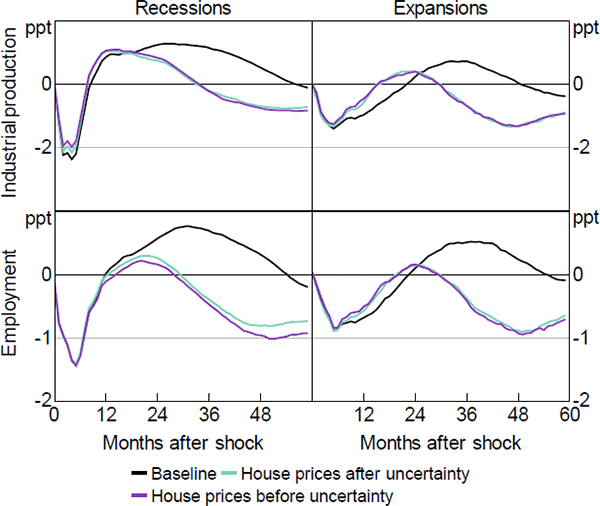
B.6 Short- versus Long-term Interest Rates
The differences documented in Figure 6 are attributed to different policies as captured by different paths of the federal funds rate. As recalled by Bernanke (2013), however, monetary policy works mainly through the term structure, and in particular via long-term interest rates. Gürkaynak, Sack and Swanson (2005) argue that the Federal Reserve has increasingly relied on communication to affect agents' expectations on long-term rates. In the context of a New-Keynesian framework featuring a term structure of interest rates, Kulish (2007) shows that long-term rates may effectively help in stabilising inflation. Following Bagliano and Favero (1998), we then enrich our VAR with the 10-year Treasury constant maturity rate (ordered after the uncertainty dummy), and re-run our estimates. We run two counterfactuals using this augmented model. The first counterfactual focuses on the response of real activity conditional on a fixed path of the federal funds rate. The aim of this counterfactual is to assess the role of systematic monetary policy when expectations about future rates, as captured by the 10-year rate, are allowed to change. In the second counterfactual, we estimate the responses to an uncertainty shock conditional on a fixed path of the long-term interest rate, that is, under the assumption that expectations about the future stance of monetary policy remain unchanged. This exercise is intended to capture the role that the 10-year rate plays in transmitting the effects of uncertainty shocks. Clearly, the 10-year rate is a combination of expectations over future monetary policy moves and the risk premium, and as such should be considered only as an imperfect proxy of expectations.
Figure B6 plots the impulse responses. Three results stand out. First, the presence of the long-term interest rate does not exert any appreciable impact on the impulse responses, which are very similar to those obtained with our baseline STVAR (shown in Figure 3). This holds true regardless of whether the economy is in a recession or in an expansion. Second, the absence of systematic policy reaction delivers a deeper recession than that predicted by our baseline exercise, even when controlling for the role of expectations about future monetary policy. However, relative to our baseline, the counterfactual recession in this case is milder. In particular, after an uncertainty shock hitting the economy in bad times, real activity returns quicker to steady state relative to the baseline case. This happens because of the role played by the long-term interest rate (possibly via changes in expectations over future monetary policy moves). A third message arising from this exercise is that shutting down the long-rate channel implies that uncertainty shocks hitting in recessions trigger a slower and less marked medium-run recovery (relative to the baseline model augmented with the long-term interest rate). The effect is even more pronounced when uncertainty shocks hit in good times.
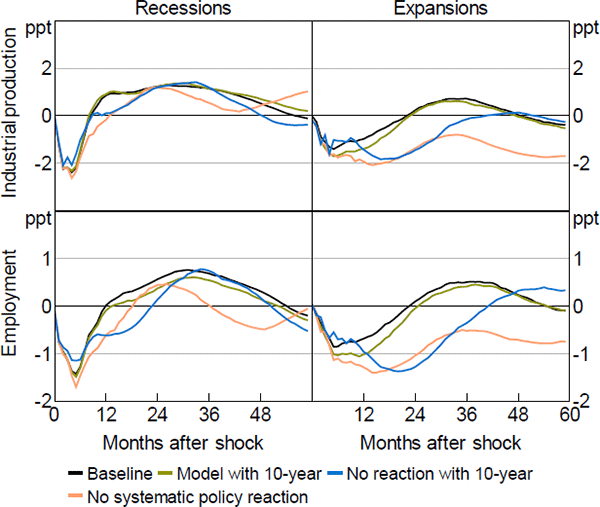
Our results suggest that the long-end of the term structure has important information to understand the effects of an unexpected increase in volatility when the economy experiences a boom. Interestingly, the two channels through which monetary policy may dampen the contractionary effects of uncertainty shocks seem to play a similar role, especially during recessions. Shutting down the short-term rate, which captures systematic monetary policy, or the long-term interest rate, which captures expectations about future monetary policy stance as well as the risk premium, appears to produce similar responses of industrial production in recessions during the first 18 months. Some differences, however, arise when we look at good times. In this case, the role of the long-term interest rate seems to be less important, while the federal funds rate matters much more. The opposite holds for employment, which turns out to be mainly affected by the long-term interest rate. Interestingly, the effects of these counterfactual policies are again larger, especially for expansions, in the medium run, but remain weak in the short run, particularly during recessions.[28]
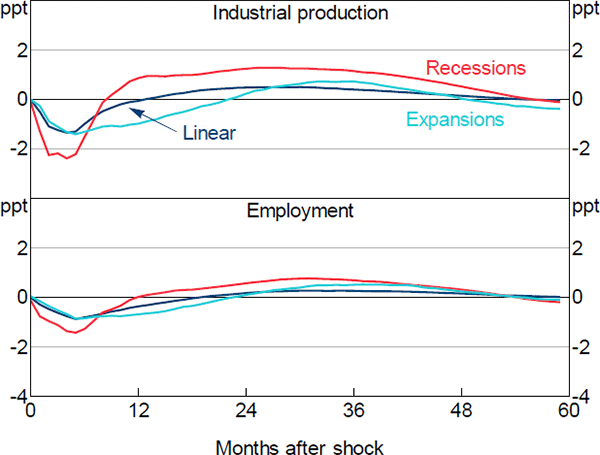
B.7 Comparison with Linear VAR
Figure B7 plots the estimated dynamic responses of industrial production and employment to an uncertainty shock obtained with a linear VAR, as well as those conditional on recessions and expansions estimated by our STVAR model. Clearly, a linear model provides a distorted picture of the real effects of uncertainty shocks over the business cycle.
Appendix C: Further Results on Risk Management-driven Policy Decisions
C.1 Risk Management-driven Policy Rate Gap: Comparison with Evans et al (2015)
The risk management-driven policy rate gap documented in Section 5.3 points to a state-dependent response of policymakers to uncertainty. Here we contrast our VAR-based results with those one can produce by working with a Taylor rule à la Evans et al (2015). Our VAR model enables us to keep track of feedback effects between the economy and the policy rate. The Taylor rule estimated by Evans et al (2015) does not. Further, they focus on the information possessed by the FOMC in real time, while our VAR framework employs revised data. Hence, if the Evans et al (2015) model produced a risk management-driven policy rate gap in line with ours, we would be reassured about the credibility of our policy rate gap. We then turn to Evans et al's (2015) model, which is the following:
where πt,k stands for the average annualised inflation rate from t to t + k, π* models the inflation target, xt,q is the average output gap from t to t + q, st is a risk management proxy, and Et denotes expectations conditional on information available to the FOMC at time t. The coefficients β, γ, and μ are fixed over time, while R* is the Taylor rate conditional on an inflation rate equal to the target, a zero output gap, and a consideration of uncertainty by the policymakers μ set to zero. In this case, the natural real rate of interest is r* = R* + π*.
Given that the FOMC has a preference for implementing variations in the policy rate in a smooth manner, and that it
does not have full control of interest rates, the polynomial 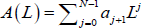 and the zero mean,
constant variance error term νt are also modelled. As regards to the former, L is
the lag operator, while N denotes the number of lags of the federal funds rate. Combining the equations
above yields to the following estimation equation:
and the zero mean,
constant variance error term νt are also modelled. As regards to the former, L is
the lag operator, while N denotes the number of lags of the federal funds rate. Combining the equations
above yields to the following estimation equation:
where bi,i = 0,1,2,3 are nonlinear functions of the structural parameters β, γ, μ, R*, and π*.
The estimation of the above equation confirms that we are able to replicate the results documented in Evans et al (2015).[29] In particular, we obtain a significant coefficient for the long-run response of the policy rate to the (standardised) VXO, whose size is −0.43.[30] To get closer to our nonlinear VAR analysis, we then estimate the following state-dependent version of the Taylor rule:
where Dt is a zero/one dummy taking a value equal to one in correspondence of quarters
classified as ‘recessions’ by the NBER and zero otherwise, and st is now the
non-standardised VXO, which is the proxy for uncertainty exploited in Bloom (2009) to identify the uncertainty shock
dummy. This equation has the potential of capturing nonlinearities in the relationship between the policy rate and
uncertainty. We estimate this equation over the sample 1987:Q1–2008:Q2 to align the end-of-sample of this
empirical analysis to the one we conduct with our VAR. Interestingly, we get a more aggressive long-run response of
the policy rate to uncertainty in recessions, and we verify that the restriction b3 = b4
is rejected at a 1 per cent level. We use this version of the Taylor rule to compute the risk management-driven
policy rate gap consistent with this nonlinear Taylor rule as 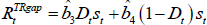 .
.
Figure C1 plots the Taylor rule policy rate gap obtained as explained above. Evidently, the values of the policy rate gap in recessions are much larger, with peaks (in absolute values) of 114 (2001:Q4), 109 (2008:Q1) and 101 (1990:Q4) basis points. If one considers that the lack of a feedback mechanism accounting for different paths of the policy rate, their effects on the economic system, and the feedback on the regressors of the Taylor rule are likely to downplay the dynamics effects induced by the role played by risk management in monetary policy setting, this result can be seen as reasonably close to the one documented in our paper.
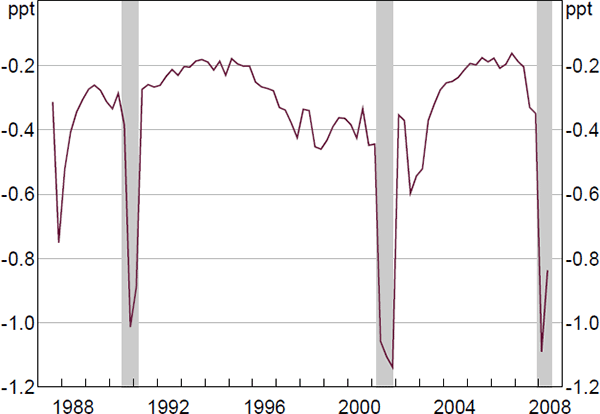
C.2 Risk Management: Narrative Evidence
Table C1 collects excerpts from the FOMC documents with references to uncertainty, risk, and risk management around the dates corresponding to the uncertainty shocks we identify. The reading of these documents confirms that uncertainty was an element carefully considered by the members of the FOMC when deciding over the federal funds rate setting.
| Uncertainty shock | Reference | Statements |
|---|---|---|
| Cuban missile crisis | FOMC HM 23/10/1962 meeting | ‘With regard to policy, Mr. Swan [President of the Federal Reserve Bank of San Francisco] expressed the view that the uncertainties presented by the international situation, and in particular the Cuban crisis, ruled out doing anything at the moment except to maintain as even a keel as possible.’ (p 33) |
| Assassination of JFK | FOMC HM 03/12/1963 meeting | ‘… there was little immediate effect that could be discerned, but that uncertainty had
been introduced into the current economic and financial scene’ (p 47) ‘System open market operations shall be conducted with a view to cushioning any unsettlement that might arise in money markets stemming from the death of President Kennedy and to maintaining about the same conditions in the money market as have prevailed in recent weeks, while accommodating moderate expansion in aggregate bank reserves.’ (p 52) |
| Vietnam build-up | FOMC HM 23/08/1966 meeting | ‘In view of those developments, the substantially increased rate structure, and the market uncertainties that existed, it seemed to him [Mr Swan, President of the Federal Reserve Bank of San Francisco] the Committee should not take further action to tighten irrespective of market forces.’ (p 91) |
| Cambodia, Kent State | FOMC MA 26/05/1970 meeting | ‘Attitudes in financial markets generally are being affected by the widespread uncertainties arising from recent international and domestic events … in view of current market uncertainties and liquidity strains, open market operations until the next meeting of the Committee shall be conducted with a view to moderating pressures on financial markets …’ (pp 3–4) |
| OPEC I, Arab-Israeli War | FOMC RPA 17–18/12/1973 meeting | ‘On November 30, however, the available members of the Committee concurred in a recommendation by the Chairman that, in light of current uncertainties regarding the economic outlook and the sensitive state of financial market psychology, current money market conditions be maintained for the time being.’ (p 7) |
| Franklin National | TIME 08/10/1974 | ‘In 1974, as Franklin began to collapse, the Federal Reserve's strategy was to lend it money in order to buy time for a bigger strategy … “The entire financial world,” Arthur Burns, the chairman of the Federal Reserve Board, told TIME shortly after, “can breathe more easily, not only in this country but abroad.”’ (Frizell 2014) |
| OPEC II | FOMC RPA 19/12/1978 meeting | ‘The uncertainties in the current situation also provided the grounds for the proposal to base the Committee's objective for money market conditions altogether on the incoming evidence on the behavior of the monetary aggregates: It was suggested that whether fundamental economic conditions were strong or weak would inevitably become evident in renewal of rapid monetary expansion or in continuation of sluggish expansion, leading in either case to appropriate objectives for money market conditions.’ (pp 10–11) |
| Afghanistan, Iran hostages | FOMC CCT 29/04/1980 conference call | ‘I [Mr Forrestal, Vice President, Federal Reserve Bank of Atlanta] think the greater risk at this point, both domestically and internationally, would be to run the risk of underkill on inflation. Without any reduction of the inflation rate we'd be making a serious mistake if we didn't [show] some resistance at this point to a precipitous decline in interest rates. I think they've fallen enough already and I would like to see the Committee opt for resisting [further declines] at the 14 to 14-1/2 percent level, wait a week to see what happens, and consult again.’ (p 6) |
| Monetary cycle turning point | FOMC RPA 24/08/1982 meeting | ‘The Committee decided that somewhat more rapid growth in the monetary aggregates would be acceptable depending upon evidence that economic and financial uncertainties were fostering unusual liquidity demands for monetary assets and were contributing to substantial volatility in interest rates.’ (p 9) |
| Black Monday | FOMC RPA 15–16/12/1987 meeting | ‘The Committee recognizes that still sensitive conditions in financial markets and uncertainties in the economic outlook may continue to call for a special degree of flexibility in open market operations.’ (p 18) |
| Gulf War I | FOMC RPA 18/12/1990 meeting | ‘Even under the assumption that the Persian Gulf situation would be more settled and oil
prices lower, restoration of the degree of confidence needed to induce a substantial upturn in
spending was not assured.’ (pp 7–8) ‘At the conclusion of the Committee's discussion, all of the members indicated that they could support a directive that called for some slight further easing in the degree of pressure on reserve positions …’ (p 14) |
| Asian crisis | FOMC M 12/11/1997 meeting | ‘The current momentum of the expansion, together with broadly supportive financial conditions
and favorable business and consumer sentiment, suggested that economic growth was likely to be well
maintained … As a consequence, the members agreed that there remained a clear risk of
additional pressures on already tight resources and ultimately on prices that could well need to be
curbed by tighter monetary policy. But the members also focused on two important influences that
were injecting new uncertainties into this outlook. Turmoil in Asian financial markets and economies
would tend to damp output and prices in the United States … The second influence was the
apparently sharp increase in productivity in the second and third quarters … While developments in Southeast Asia were not expected to have much effect on the U.S. economy, global financial markets had not yet settled down and further adverse developments could have greater-than-anticipated spillover effects on the ongoing expansion. In this environment, with markets still skittish, a tightening of U.S. monetary policy risked an oversized reaction … At the conclusion of the Committee's discussion, all but one member supported a directive that called for maintaining conditions in reserve markets that were consistent with an unchanged federal funds rate of about 5-1/2 percent and that retained a bias toward the possible firming of reserve conditions and a higher federal funds rate during the intermeeting period.’ |
| Russian, LTCM default | FOMC M 29/09/1998 meeting | ‘In a telephone conference held on October 15, 1998, the Committee members discussed recent
economic and financial developments and their implications for monetary policy. Risk aversion in
financial markets had increased further since the Committee's meeting in September, raising
volatility and risk spreads even more, eroding market liquidity, and constraining borrowing and
lending in a number of sectors of the financial markets. Although indications of any softening in
the pace of the economic expansion across the country remained sparse, the widespread signs of
deteriorating business confidence and evidence of less accommodative domestic financial conditions
suggested that the downside risks to the expansion had continued to mount. ‘Against this background, a consensus emerged in favor of a 1/4 percentage point reduction in the federal funds rate …’ |
| 9/11 | FOMC M 06/11/2001 meeting | ‘The staff forecast prepared for this meeting emphasized the continuing wide range of
uncertainty surrounding the outlook in the wake of the September attacks. The mild downturn in
economic activity in the third quarter was seen as likely to deepen over the remainder of the year
and to continue for a time next year. However, the cumulative easing that had occurred in the stance
of monetary policy, coupled with the fiscal stimulus already in place and prospective additional
measures, would provide support for economic activity … However, the strength and timing of
the eventual recovery remained subject to question especially in light of the marked degree of
uncertainty that surrounded the prospects for further fiscal policy legislation, developments in the
war against terrorism, and weakness in foreign economies … In the Committee's discussion of policy for the intermeeting period ahead, all the members indicated that they could support a proposal calling for further easing in reserve conditions consistent with a 50 basis point reduction in the federal funds rate to a level of 2 percent.’ |
| Worldcom, Enron | FOMC M 06/11/2002 meeting | ‘Business investment expenditures continued to be constrained by a high degree of uncertainty
and related caution … All the members indicated that, in light of the contemplated 50 basis point easing action, they could support a shift in the Committee's assessment of the risks to the economy from tilted toward economic weakness to balanced for the foreseeable future …’ |
| Gulf War II | FOMC M 18/03/2003 meeting | ‘The staff forecast prepared for this meeting continued to suggest that economic expansion
would be muted for a time. Faced with the likely onset of war in the very near term and the large
uncertainties relating to its aftermath, businesses and consumers were likely to hold down their
spending … In the Committee's discussion of current and prospective economic
developments, members commented that an unusually high degree of uncertainty had made it very
difficult to assess the factors underlying the performance of the economy … In light of these considerable uncertainties, the members agreed that heightened surveillance of evolving economic trends would be especially useful in the weeks ahead … the Committee in the immediate future seeks conditions in reserve markets consistent with maintaining the federal funds rate at an average of around 1-1/4 percent.’ |
|
Notes: FOMC HM: FOMC Historical Minutes, FOMC MA: FOMC Minutes of Actions, FOMC RPA: FOMC Record of Policy Actions, FOMC CCT: FOMC Conference Call Transcript, FOMC M: FOMC Minutes Sources: Federal Open Market Committee: Transcripts and Other Historical Materials; Frizell (2014) |
||
References
Aastveit KA, GJ Natvik and S Sola (2013), ‘Economic Uncertainty and the Effectiveness of Monetary Policy’, Norges Bank Working Paper No 2013|17.
Abadir KM, G Caggiano and G Talmain (2013), ‘Nelson–Plosser Revisited: The ACF Approach’, Journal of Econometrics, 175(1), pp 22–34.
Alessandri P and H Mumtaz (2014), ‘Financial Regimes and Uncertainty Shocks’, Queen Mary University of London, School of Economics and Finance Working Paper No 729.
Auerbach A and Y Gorodnichenko (2012), ‘Measuring the Output Responses to Fiscal Policy’, American Economic Journal: Economic Policy, 4(2), pp 1–27.
Bachmann R, S Elstner and ER Sims (2013), ‘Uncertainty and Economic Activity: Evidence from Business Survey Data’, American Economic Journal: Macroeconomics, 5(2), pp 217–249.
Bachmann R and ER Sims (2012), ‘Confidence and the Transmission of Government Spending Shocks’, Journal of Monetary Economics, 59(3), pp 235–249.
Bagliano FC and CA Favero (1998), ‘Measuring Monetary Policy with VAR Models: An Evaluation’, European Economic Review, 42(6), pp 1069–1112.
Baker SR, N Bloom and SJ Davis (2016), ‘Measuring Economic Policy Uncertainty’, The Quarterly Journal of Economics, 131(4), pp 1593–1636.
Baley I and JA Blanco (2016), ‘Menu Costs, Uncertainty Cycles, and the Propagation of Nominal Shocks’, Barcelona GSE Working Paper No 918.
Basu S and B Bundick (2015), ‘Endogenous Volatility at the Zero Lower Bound: Implications for Stabilization Policy’, Federal Reserve Bank of Kansas City Research Working Paper No 15-01.
Basu S and B Bundick (2017), ‘Uncertainty Shocks in a Model of Effective Demand’, Econometrica, 85(3), pp 937–958.
Bekaert G, M Hoerova and M Lo Duca (2013), ‘Risk, Uncertainty and Monetary Policy’, Journal of Monetary Economics, 60(7), pp 771–788.
Berger D and J Vavra (2014), ‘Measuring How Fiscal Shocks Affect Durable Spending in Recessions and Expansions’, The American Economic Review, 104(5), pp 112–115.
Berger D and J Vavra (2015), ‘Consumption Dynamics during Recessions’, Econometrica, 83(1), pp 101–154.
Bernanke BS (2013), ‘Long-Term Interest Rates’, Dinner Remarks given at a Research Conference ‘The Past and Future of Monetary Policy’, Federal Reserve Bank of San Francisco, San Francisco, 1 March.
Blanchard O (2009), ‘(Nearly) Nothing to Fear but Fear Itself’, The Economist, 31 January–6 February, p 76.
Bloom N (2009), ‘The Impact of Uncertainty Shocks’, Econometrica, 77(3), pp 623–685.
Bloom N (2014), ‘Fluctuations in Uncertainty’, Journal of Economic Perspectives, 28(2), pp 153–176.
Bloom N (2017), ‘Observations on Uncertainty’, The Australian Economic Review, 50(1), pp 79–84.
Bloom N, M Floetotto, N Jaimovich, I Saporta-Eksten, and SJ Terry (2014), ‘Really Uncertain Business Cycles’, US Census Bureau, Center for Economic Studies Paper No CES 14-18.
Cacciatore M and F Ravenna (2015), ‘Uncertainty, Wages, and the Business Cycle’, Paper presented at the 29th Annual Meeting of the Canadian Macroeconomics Study Group, Montréal, 6–7 November.
Caggiano G and E Castelnuovo (2011), ‘On the Dynamics of International Inflation’, Economics Letters, 112(2), pp 189–191.
Caggiano G, E Castelnuovo, V Colombo and G Nodari (2015), ‘Estimating Fiscal Multipliers: News from a Non-Linear World’, Economic Journal, 125(584), pp 746–776.
Caggiano G, E Castelnuovo and JM Figueres (2017), ‘Economic Policy Uncertainty and Unemployment in the United States: A Nonlinear Approach’, Economics Letters, 151, pp 31–34.
Caggiano G, E Castelnuovo and N Groshenny (2014), ‘Uncertainty Shocks and Unemployment Dynamics in U.S. Recessions’, Journal of Monetary Economics, 67, pp 78–92.
Caggiano G, E Castelnuovo and G Pellegrino (2017), ‘Estimating the Real Effects of Uncertainty Shocks at the Zero Lower Bound’, European Economic Review, 100, pp 257–272.
Caldara D, C Fuentes-Albero, S Gilchrist, and E Zakrajšek (2016), ‘The Macroeconomic Impact of Financial and Uncertainty shocks’, European Economic Review, 88, pp 185–207.
Canova F (2007), Methods for Applied Macroeconomic Research, Princeton University Press, Princeton.
Carriero A, TE Clark and M Marcellino (2016), ‘Measuring Uncertainty and Its Impact on the Economy’, Federal Reserve Bank of Cleveland Working Paper No 16-22.
Casarin R, C Foroni, M Marcellino and F Ravazzolo (2016), ‘Uncertainty through the Lenses of a Mixed-Frequency Bayesian Panel Markov Switching Model’, Innocenzo Gasparini Institute for Economic Research IGIER Working Paper No 585.
Chernozhukov V and H Hong (2003), ‘An MCMC Approach to Classical Estimation’, Journal of Econometrics, 115(2), pp 293–346.
Cogley T and JM Nason (1995), ‘Effects of the Hodrick-Prescott Filter on Trend and Difference Stationary Time Series: Implications for Business Cycle Research’, Journal of Economic Dynamics & Control, 19(1–2), pp 253–278.
Eickmeier S, N Metiu and E Prieto (2016), ‘Time-Varying Volatility, Financial Intermediation and Monetary Policy’, Australian National University, Centre for Applied Macroeconomic Analysis CAMA Working Paper No 32/2016.
Evans C, J Fisher, F Gourio and S Krane (2015), ‘Risk Management for Monetary Policy Near the Zero Lower Bound’, Federal Reserve Bank of Chicago Working Paper No 2015-03.
Ferrara L and P Guérin (2015), ‘What Are the Macroeconomic Effects of High-Frequency Uncertainty Shocks?’, EconomiX Working Paper No 2015-12.
Frizell S (2014), ‘Could a 40-Year-Old Bank Collapse Have Saved the U.S. Economy?’, Time site, 8 October. Available at <http://time.com/3479314/franklin-national-bank>.
Furlanetto F, F Ravazzolo and S Sarferaz (2014), ‘Identification of Financial Factors in Economic Fluctuations’, Norges Bank Working Paper No 09|2014.
Gilchrist S and E Zakrajšek (2012), ‘Credit Spreads and Business Cycle Fluctuations’, The American Economic Review, 102(4), pp 1692–1720.
Gnabo J-Y and DN Moccero (2015), ‘Risk Management, Nonlinearity and Aggressiveness in Monetary Policy: The Case of the US Fed’, Journal of Banking & Finance, 55, pp 281–294.
Greenspan A (2004), ‘Risk and Uncertainty in Monetary Policy’, The American Economic Review, 94(2), pp 33–40.
Gürkaynak RS, B Sack and E Swanson (2005), ‘The Sensitivity of Long-Term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models’, The American Economic Review, 95(1), pp 425–436.
Hansen B (1999), ‘Testing for Linearity’, Journal of Economic Surveys, 13(5), pp 551–576.
Jurado K, SC Ludvigson and S Ng (2015), ‘Measuring Uncertainty’, The American Economic Review, 105(3), pp 1177–1216.
Knight FH (1921), Risk, Uncertainty, and Profit, Houghton Mifflin Company, Boston.
Koop G, MH Pesaran and SM Potter (1996), ‘Impulse Response Analysis in Nonlinear Multivariate Models’, Journal of Econometrics, 74(1), pp 119–147.
Koop G and SM Potter (1999), ‘Dynamic Asymmetries in U.S. Unemployment’, Journal of Business & Economic Statistics, 17(3), pp 298–312.
Kulish M (2007), ‘Should Monetary Policy Use Long-Term Rates?’, B.E. Journal of Macroeconomics, 7(1), Advances, Article 15.
Leduc S and Z Liu (2016), ‘Uncertainty Shocks are Aggregate Demand Shocks’, Journal of Monetary Economics, 82, pp 20–35.
Ludvigson SC, S Ma and S Ng (2015), ‘Uncertainty and Business Cycles: Exogenous Impulse or Endogenous Response?’, NBER Working Paper No 21803.
Luukkonen R, P Saikkonen and T Teräsvirta (1988), ‘Testing Linearity against Smooth Transition Autoregressive Models’, Biometrika, 75(3), pp 491–499.
Mittnik S (1990), ‘Modelling Nonlinear Processes With Generalized Autoregressions’, Applied Mathematics Letters, 3(4), pp 71–74.
Morley J and J Piger (2012), ‘The Asymmetric Business Cycle’, The Review of Economics and Statistics, 94(1), pp 208–221.
Morley J, J Piger and P-L Tien (2013), ‘Reproducing Business Cycle Features: Are Nonlinear Dynamics a Proxy for Multivariate Information?’, Studies in Nonlinear Dynamics and Econometrics, 17(5), pp 483–498.
Mumtaz H and P Surico (2015), ‘The Transmission Mechanism in Good and Bad Times’, International Economic Review, 56(4), pp 1237–1260.
Nodari G (2014), ‘Financial Regulation Policy Uncertainty and Credit Spreads in the US’, Journal of Macroeconomics, 41, pp 122–132.
Orlik A and L Veldkamp (2014), ‘Understanding Uncertainty Shocks and the Role of Black Swans’, NBER Working Paper No 20445.
Pellegrino G (2017a), ‘Uncertainty and Monetary Policy in the US: A Journey into Non-Linear Territory’, Melbourne Institute Working Paper No 6/17.
Pellegrino G (2017b), ‘Uncertainty and the Real Effects of Monetary Policy Shocks in the Euro Area’, Melbourne Institute Working Paper No 15/17.
Ramey V and S Zubairy (forthcoming), ‘Government Spending Multipliers in Good Times and in Bad: Evidence from U.S. Historical Data’, Journal of Political Economy.
Rossi B and T Sekhposyan (2015), ‘Macroeconomic Uncertainty Indices Based on Nowcast and Forecast Error Distributions’, The American Economic Review, 105(5), pp 650–655.
Rossi B and T Sekhposyan (2017), ‘Macroeconomic Uncertainty Indices for the Euro Area and Its Individual Member Countries’, Empirical Economics, 53(1), pp 41–62.
Rossi B, T Sekhposyan and M Soupre (2016), ‘Understanding the Sources of Macroeconomic Uncertainty’, Centre for Economic Policy Research Discussion Paper 11415.
Scotti C (2016), ‘Surprise and Uncertainty Indexes: Real-Time Aggregation of Real-Activity Macro-Surprises’, Journal of Monetary Economics, 82, pp 1–19.
Seneca M (2016), ‘Risk Shocks Close to the Zero Lower Bound’, Bank of England Staff Working Paper No 606.
Sichel DE (1993), ‘Business Cycle Asymmetry: A Deeper Look’, Economic Inquiry, 31(2), pp 224–236.
Sims CA and T Zha (2006), ‘Were There Regime Switches in U.S. Monetary Policy?’, The American Economic Review, 96(1), pp 54–81.
Stock JH and MW Watson (2012), ‘Disentangling the Channels of the 2007–09 Recession’, Brookings Papers on Economic Activity, Spring, pp 81–135.
Tenreyro S and G Thwaites (2016), ‘Pushing on a String: US Monetary Policy is Less Powerful in Recessions’, American Economic Journal: Macroeconomics, 8(4), pp 43–74.
Teräsvirta T, D Tjøstheim and CWJ Granger (2010), Modelling Nonlinear Economic Time Series, Advanced Texts in Econometrics, Oxford University Press, Oxford.
Teräsvirta T and Y Yang (2014), ‘Linearity and Misspecification Tests for Vector Smooth Transition Regression Models’, Aarhus University, Department of Economics and Business, Center for Research in Econometric Analysis of Time Series CREATES Research Paper 2014-4.
van Dijk D, T Teräsvirta and PH Franses (2002), ‘Smooth Transition Autoregressive Models — A Survey of Recent Developments’, Econometric Reviews, 21(1), pp 1–47.
Vavra J (2014), ‘Inflation Dynamics and Time-Varying Volatility: New Evidence and an Ss Interpretation’, The Quarterly Journal of Economics, 129(1), pp 215–258.
Weise CL (1999), ‘The Asymmetric Effects of Monetary Policy: A Nonlinear Vector Autoregression Approach’, Journal of Money, Credit and Banking, 31(1), pp 85–108.
Yellen J (2015), ‘Transcript of Chair Yellen's Press Conference’, Federal Open Market Committee, Washington DC, 17 September.
Acknowledgements
We would like to thank Sami Alpanda, Viola Angelini, Leon Berkelmans, Nicholas Bloom, Anthony Brassil, Steven J Davis, Mardi Dungey, Luci Ellis, Christopher Gibbs, Klodiana Istre, Henrik Jensen, Gunes Kamber, Mariano Kulish, Sydney Ludvigson, Chandler Lutz, James Morley, Antonio Nicolò, Adrian Pagan, Morten Ravn, Søren Hove Ravn, Federico Ravenna, Daniel Rees, John Simon, Jesús Fernández-Villaverde, Benjamin Wong, and participants at presentations held at the Stanford Institute for Theoretical Economics Workshop, Conference on Computing in Economics and Finance (Oslo), Workshop of the Australasian Macroeconomics Society (Melbourne), Western Economic Association Conference (Wellington), Deutsche Bundesbank, Bank of Finland, Norges Bank, Copenhagen Business School, Reserve Bank of Australia, Monash University, and the Universities of Copenhagen, Melbourne, New South Wales (Sydney), Padova and Surrey for their useful comments and suggestions. The opinions expressed do not necessarily reflect those of the Bank of Finland or the Reserve Bank of Australia. The authors are solely responsible for any errors. Financial support from the Australian Research Council via the Discovery Grant DP160102281 is gratefully acknowledged.
Footnotes
Department of Economics, Monash University [*]
Department of Economics, University of Melbourne and Melbourne Institute of Applied Economic and Social Research [**]
Economic Research Department, Reserve Bank of Australia [***]
Spikes in uncertainty indicators occur also in good times. For instance, the volatility index we use registered a substantial increment after Black Monday (19 October 1987), during a period classified as expansionary by the NBER. In general, however, increases in uncertainty during bad times are much more abrupt than those occurring in good times. [1]
We show the linear effects of uncertainty shocks, computed with our model, in Appendix B. [2]
Carriero, Clark and Marcellino (2016) model a large dataset of macroeconomic and financial variables and compute the effects of macroeconomic and financial uncertainty shocks. They find that macroeconomic uncertainty has a large and significant effect on real activity, but has a limited impact on financial variables. Differently, financial uncertainty has an impact on both financial and macroeconomic indicators. Given the inclusion of the S&P 500 index and measures of interest rates in our study, our focus on a financial-related uncertainty proxy is also intended to maximise the likelihood of capturing the real effects of uncertainty shocks via movements in financial markets. [3]
As recalled by Bloom (2014), Knight (1921) defined uncertainty as people's inability to form a probability distribution over future outcomes. Differently, he defined risk as people's inability to predict which outcome will be drawn from a known probability distribution. Following most of the empirical literature, we do not distinguish between the two concepts, and use the VXO-related dummy as a proxy for uncertainty. We acknowledge though that this indicator is a mixture of both risk and uncertainty. See Bekaert, Hoerova and Lo Duca (2013) and Rossi, Sekhposyan and Soupre (2016) for investigations that disentangle the effects of risk and uncertainty. [4]
Our model specification closely follows that in Bloom (2009), which we take as a starting point for our analysis. However, and unlike Bloom, we do not Hodrick-Prescott (HP) filter these variables, except the VXO series we use to compute the uncertainty dummy. As shown by Cogley and Nason (1995), HP-filtering may induce spurious cyclical fluctuations, which may bias our results. Exercises conducted with HP-filtered variables, as in Bloom (2009), returned results qualitatively in line with those documented in this paper. These results are available upon request and are consistent with the robustness check in Bloom (2009, Fig A3, p 679). [5]
We use the HP-detrended VXO series to construct the dummy variable for consistency with Bloom (2009). Using the non-filtered level of the VXO to construct the dummy delivers a similar set of shocks. Further, we check the robustness of our results to alternative uncertainty proxies (see Appendix B). [6]
Working with linear VARs, Furlanetto, Ravazzolo and Sarferaz (2014) identify uncertainty shocks using sign restrictions, while Caldara et al (2016) adopt a penalty approach. We leave the investigation of the properties of these approaches in a nonlinear STVAR context to future research. [7]
One example would be changes in forecasts for the real economy, which are not modelled as our specification already includes a large set of variables. Additionally, and as previously mentioned, our uncertainty proxy is likely a stand-in for a mixture of risk and uncertainty. These are important observations to bear in mind when interpreting our results. [8]
A simpler, alternative approach would be that of adding an interaction term involving uncertainty and an indicator of the business cycle to the otherwise linear model à la Bloom (2009). The resulting interacted VAR would have the potential to discriminate between responses to uncertainty in recessions/expansions. We prefer to model a STVAR for two reasons. First, it does not require us to take a stand on the features of the interaction term (e.g. number of lags, timing of the cross products). Second, it is much less prone to instabilities, a problem often affecting interacted VARs when involving interaction terms of order two or higher (for a discussion, see Mittnik (1990)). [9]
Appendix B discusses the robustness of our results to the use of the unemployment rate as transition indicator. [10]
This choice is consistent with a threshold value  equal to −1.01, which corresponds to a threshold value for the non-standardised moving average of the growth rate of industrial production equal to 0.13 per cent. This last figure is obtained by considering the sample mean of the non-standardised growth rate of industrial production (in moving average terms), which is equal to 0.40, and its standard deviation, which reads 0.27. Then, its corresponding threshold value is obtained by ‘inverting’ the formula we employed to obtain the standardised transition indicator z, that is,
equal to −1.01, which corresponds to a threshold value for the non-standardised moving average of the growth rate of industrial production equal to 0.13 per cent. This last figure is obtained by considering the sample mean of the non-standardised growth rate of industrial production (in moving average terms), which is equal to 0.40, and its standard deviation, which reads 0.27. Then, its corresponding threshold value is obtained by ‘inverting’ the formula we employed to obtain the standardised transition indicator z, that is,  .
[11]
.
[11]
The calibration of γ in both sub-samples is lower than that for the full sample, despite the frequency of recessions being higher in the first sub-sample and lower in the second. This is because the calibration depends on the values taken by the transition variable (industrial production) in each period considered. Thus, there is no reason to expect the value of γ to be linear with respect to the frequency of recessions. [12]
A potential weakness associated with our modelling approach is the implicit assumption that the model parameters do not change over time (they change only across states of the business cycle). Modelling a time-varying parameters STVAR model is a possibility that we leave for future research. [13]
In principle, one could estimate the STVAR model via maximum likelihood. However, since the model is highly nonlinear and has many parameters, using standard optimisation routines is problematic. Under standard conditions, the algorithm put forth by Chernozhukov and Hong finds a global optimum in terms of fit as well as the distributions of parameter estimates. [14]
Following Koop et al (1996), our GIRFs are computed as follows. First, we draw an initial condition, that is, starting values for the lags as well as the transition indicator z, which provides us with the starting value for F(z). Then, we simulate two scenarios, one with all the shocks identified with the Cholesky decomposition of the VCV matrix, and another one with the same shocks plus δ > 0 corresponding to the first realisation of the uncertainty shock. The difference between these two scenarios (each of which accounts for the evolution of F(z) by keeping track of the evolution of industrial production) gives us the GIRFs to an uncertainty shock of size δ. Appendix A provides additional details on the algorithm we employed to compute the GIRFs. [15]
We model nonlinearities only with respect to the state of the economy. Impulse responses may also depend on the size and sign of the shock. While we do not investigate the effects of unexpected decreases in uncertainty, robustness checks suggest a negligible impact as for the size of the shock. [16]
The baseline and counterfactual scenarios produce similar responses for the first few months after the shock. This is due to the relevance of initial conditions, which are dominant during the first periods. In fact, initial conditions heavily influence the evolution of the transition indicator and, therefore, the probability of being in a recession. Systematic policy takes time before notably affecting the economic system and, consequently, the value of the logistic function in our STVAR. However, as periods go by, policy exerts an impact on the evolution of the economic system, above all in expansions. [17]
Controlling for fiscal policy in our STVAR would require us to work with a different sample as most fiscal aggregates are available only at a quarterly frequency. Data aggregation could lead to a loss of useful information, as it would reduce the number of observations available for estimation. Therefore, we leave the investigation of potentially nonlinear fiscal-monetary policy interactions for future research. [18]
This counterfactual differs from the one conducted in Section 5.1 in two ways. First, we constrain only the coefficients on uncertainty (and not on all the other variables as we did before). Second, instead of computing impulse responses to an uncertainty shock, we iterate the model forward to produce the alternative ‘no risk management’ path of the variables included in our analysis. [19]
We do not explore the counterfactual paths of wages and hours as our VAR model might not adequately capture labour market dynamics. These variables are included in the model mostly to help explain aggregate employment and industrial production. [20]
The recovery from the Great Recession has advanced sufficiently far and domestic spending appears sufficiently robust that an argument can be made for a rise in interest rates at this time. We discussed this possibility at our meeting. However, in light of the heightened uncertainties abroad and a slightly softer expected path for inflation, the Committee judged it appropriate to wait for more evidence, including some further improvement in the labor market, to bolster its confidence that inflation will rise to 2 percent in the medium term (Yellen 2015).[21]
To understand how quantitatively close our results are to Evans et al's (2015), we conduct the following exercise. We estimate their Taylor rule over the sample 1987:Q1–2008:Q2 by allowing for a nonlinear response of the policy rate in NBER recessions/expansions to uncertainty, which is proxied by the VXO. Then, we produce the ‘Taylor rule risk management-driven policy rate gap’ by taking the difference between the historical policy rate and the one produced by sticking to historical values of core inflation, the output gap, and (lagged realisations of) the policy rate, in a version of the Taylor rule conditional on a zero response to uncertainty. The resulting Taylor rule policy rate gap: i) displays large realisations (in absolute terms) in recessions, and ii) points to a value as large as 114 basis points in 2001:Q4. Details on the derivation of the Taylor rule rate gap are documented in Appendix C. [22]
This section heavily draws on Auerbach and Gorodnichenko's (2012) ‘Appendix: Estimation Procedure’. [23]
The choice p = 12 is due to the number of moving average terms (12) of our transition variable, zt. [24]
We consider the distribution of parameters rather than their mean values to allow for parameter uncertainty, as suggested by Koop et al (1996). [25]
The terror shocks are: the assassination of JFK (November 1963), the 9/11 terrorist attacks (September 2001). The war shocks are: the Cuban missile crisis (October 1962), the Vietnam build-up (August 1966), Cambodia and Kent State (May 1970), Afghanistan and Iran hostages (March 1980), the Gulf War I (October 1990), the Gulf War II (February 2003). The oil shocks are dated December 1973 and November 1978. [26]
The index is available here: <http://www.econ.yale.edu/~shiller/data/Fig2-1.xls> at a quarterly frequency. We moved to monthly frequencies via a cubic interpolation of the quarterly series and modelled the index in logs. [27]
Obviously, caution should be used in interpreting these results, which come from exercises that are subject to the Lucas critique. Ideally, one should build up a model which meaningfully features uncertainty shocks, financial frictions, short- and long-term interest rates, and mechanisms inducing a nonlinear response of real aggregates to uncertainty shocks. We see our results as supporting this research agenda. [28]
The replication files containing their datasets are available at <https://www.chicagofed.org/publications/working-papers/2015/wp2015-03>. We focus on the 30-day forward average of the target rate following each FOMC meeting as policy rate, and on the Greenbook measures of CPI inflation and output gap expectations for modelling the response to inflation and real activity. A detailed description of the data is provided in Evans et al's Appendix, which is available here: <https://www.chicagofed.org/~/media/publications/working-papers/2015/wp2015-03-main-appendix-pdf.pdf?la=en>. Given our choice of proxying uncertainty with the VXO, we focus on the case in which the measure of uncertainty is the VXO. Following Evans et al, we first standardise the VXO in order to interpret the long-run response of the policy rate as the reaction to a one standard deviation increase in uncertainty. We then estimate the last equation reported above via least squares, focusing on the sample 1987:Q1–2008:Q4, which is the same sample they focus on. We account for heteroskedasticity by modelling the White-correction of the VCV matrix, as they do. [29]
See Table 9 in Evans et al (2015, p 50). [30]