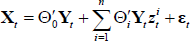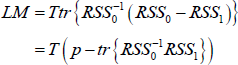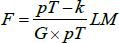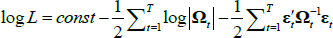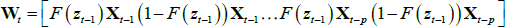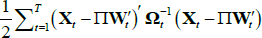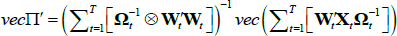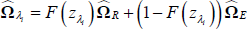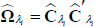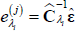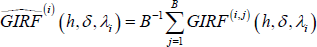RDP 2017-06: Uncertainty and Monetary Policy in Good and Bad Times Appendix A: Technical Details
October 2017
This appendix documents statistical evidence in favour of a nonlinear relationship between the endogenous variables included in our STVAR. It also provides details on the estimation procedure of our nonlinear VARs, and on the computation of the GIRFs.
A.1 Statistical Evidence in Favour of Nonlinearities
To detect nonlinear dynamics at a multivariate level, we apply the test proposed by Teräsvirta and Yang (2014). Their framework is particularly well suited for our analysis since it proposes testing the null hypothesis of linearity versus a specified nonlinear alternative, that of a STVAR with a single transition variable.
Consider the following p-dimensional 2-regime approximate logistic STVAR model:
where Xt is the (p × 1) vector of endogenous variables, Yt = [Xt − 1|…|Xt − k|∝] is the ((k × p + q) × 1) vector of exogenous variables (including endogenous variables lagged k times and a column vector of constants ∝), zt is the transition variable, and Θ0 and Θi are matrices of parameters. In our case, the number of endogenous variables is p = 8, the number of exogenous variables is q = 1, and the number of lags is k = 6. Under the null hypothesis of linearity, Θi = 0 ∀i.
The Teräsvirta-Yang test for linearity versus the STVAR model can be performed as follows:
- Estimate the restricted model (Θi = 0 ∀i) by regressing Xt on Yt. Collect the residuals E and compute the matrix of residual sum of squares RSS0 = E’E.
-
Run an auxiliary regression of E on (Yt,Zn)
where
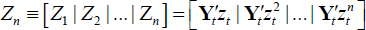 . Collect the
residuals Ξ and compute the matrix residual sum of squares RSS1 = Ξ’Ξ.
. Collect the
residuals Ξ and compute the matrix residual sum of squares RSS1 = Ξ’Ξ.
-
Compute the test statistic
Under the null hypothesis, the test statistic is distributed as a χ2 with p(kp + q) degrees of freedom. For our model, we get a value of LM = 1992 with a corresponding p-value equal to zero. The LM statistic has been computed by fixing the value of the order of the Taylor expansion n = 3, as suggested by Luukkonen, Saikkonen and Teräsvirta (1988). We note, however, that the null of linearity can be rejected also for n = 2. - As pointed out by Teräsvirta and Yang (2014), however, in small samples the LM-type test might suffer from positive size distortion, that is, the empirical size of the test exceeds the true asymptotic size. We then also employ the following rescaled LM test statistic: where G is the number of restrictions. The rescaled test statistic follows an F(G,pT − k) distribution. In our case, we get F = 13.54, with a p-value approximately equal to zero.
A.2 Estimation of the Nonlinear VARs
Our model (1)–(4) is estimated via maximum likelihood.[23] Its log-likelihood reads as follows:
where 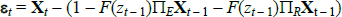 is the vector of
residuals. Our goal is to estimate the parameters
is the vector of
residuals. Our goal is to estimate the parameters 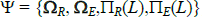 ,
,
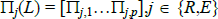 . We do so by
conditioning on a given value for the smoothness parameter γ, which is calibrated as described in the
text. The high nonlinearity of the model and its many parameters make its estimation with standard optimisation
routines problematic. Following Auerbach and Gorodnichenko (2012), we employ the procedure described below.
. We do so by
conditioning on a given value for the smoothness parameter γ, which is calibrated as described in the
text. The high nonlinearity of the model and its many parameters make its estimation with standard optimisation
routines problematic. Following Auerbach and Gorodnichenko (2012), we employ the procedure described below.
Conditional on {γ,ΩR,ΩE}, the model is linear in {∏R(L),∏E(L)}.
Then for a given guess on {γ,ΩR,ΩE}, the
coefficients {∏R(L),∏E(L)} can be estimated by
minimising 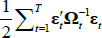 . This can
be seen by re-writing the regressors as follows. Let:
. This can
be seen by re-writing the regressors as follows. Let:
be the extended vector of regressors, and ∏ =
[∏R(L),∏E(L)]. Then, we can write 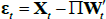 . Consequently, the
objective function becomes:
. Consequently, the
objective function becomes:
It can be shown that the first-order condition with respect to ∏ is:
This procedure iterates over different sets of values for {ΩR, ΩE}, conditional on a given value for γ. For each set of values, ∏ is obtained and the log L computed.
Given that the model is highly nonlinear in its parameters, several local optima might be present. Hence, it is
recommended to try different starting values for {ΩR, ΩE} and then
explore the robustness of the estimates to different values of γ. To ensure positive definiteness of
the variance-covariance matrices, we focus on the alternative vector of parameters 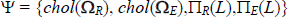 , where chol
implements a Cholesky decomposition.
, where chol
implements a Cholesky decomposition.
The construction of confidence intervals for the parameter estimates is complicated by the nonlinear structure of the problem. We compute them by appealing to a Markov Chain Monte Carlo (MCMC) algorithm developed by Chernozhukov and Hong (2003) (CH hereafter). This method delivers both a global optimum and densities for the parameter estimates.
CH estimation is implemented via a Metropolis-Hastings algorithm. Given a starting value Ψ(0), the procedure constructs chains of length N of the parameters of our model following these steps:
Step 1. Draw a candidate vector of parameter values Θ(n) = Ψ(n) + ψ(n) for the chain's n + 1 state, where Ψ(n) is the current state and Ψ(n) is the vector of iid shocks drawn from N(0,Ωψ), and Ωψ is a diagonal matrix.
Step 2. Set the n + 1 state of the chain Ψ(n + 1) =
Θ(n) with probability 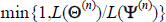 where L(Θ(n)) is the value of the likelihood function conditional on the candidate
vector of parameter values, and L(Ψ(n)) the value of the likelihood function
conditional on the current state of the chain. Otherwise, set Ψ(n + 1) =
Ψ(n).
where L(Θ(n)) is the value of the likelihood function conditional on the candidate
vector of parameter values, and L(Ψ(n)) the value of the likelihood function
conditional on the current state of the chain. Otherwise, set Ψ(n + 1) =
Ψ(n).
The starting value Θ(0) is computed by working with a second-order Taylor approximation of the model
(1)–(4) (see the main text), so that the model can be written as regressing Xt
on lags of Xt,
Xtzt and 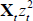 . The
residuals from this regression are employed to fit the expression for the reduced-form time-varying
variance-covariance matrix of the VAR using maximum likelihood to estimate ΩR and
ΩE. Conditional on these estimates and given a calibration for γ, we can
construct Ωt. Conditional on Ωt, we can get starting values for
∏R(L) and ∏E(L).
. The
residuals from this regression are employed to fit the expression for the reduced-form time-varying
variance-covariance matrix of the VAR using maximum likelihood to estimate ΩR and
ΩE. Conditional on these estimates and given a calibration for γ, we can
construct Ωt. Conditional on Ωt, we can get starting values for
∏R(L) and ∏E(L).
Given a calibration for the initial (diagonal matrix) ΩΨ, a scale factor is adjusted to generate an acceptance rate close to 0.3, a typical choice for this kind of simulation (Canova 2007). We employ N 50,000 draws for our estimates, and retain the last 20 per cent for inference. Checks performed with N = 200,000 draws delivered very similar results.
As shown by CH, 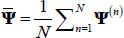 is a
consistent estimate of Ψ under regularity assumptions on maximum likelihood estimators. Moreover, the
covariance matrix of Ψ is given by
is a
consistent estimate of Ψ under regularity assumptions on maximum likelihood estimators. Moreover, the
covariance matrix of Ψ is given by 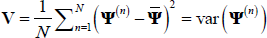 , that is the variance of the estimates in the
generated chain.
, that is the variance of the estimates in the
generated chain.
A.3 Generalised Impulse Response Functions
We compute the generalised impulse response functions from our STVAR model by following the approach proposed by Koop et al (1996). The algorithm features the following steps.
- Consider the entire available observations, with sample size t = 1962:M7,…, 2008:M6, with T = 552, and construct the set of all possible histories Λ of length p = 12:{λi ∈ Λ}. Λ will contain T − p + 1 histories λi.[24]
-
Separate the set of all recessionary histories from that of all expansionary histories. For each
λi calculate the transition variable
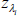 . If
. If 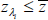 = −1.01 per
cent, then λi ∈ ΛR, where
ΛR is the set of all recessionary histories. If
= −1.01 per
cent, then λi ∈ ΛR, where
ΛR is the set of all recessionary histories. If 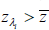 =
−1.01 per cent, then λi ∈ ΛE, where
ΛE is the set of all expansionary histories.
=
−1.01 per cent, then λi ∈ ΛE, where
ΛE is the set of all expansionary histories.
-
Select at random one history λi ∈ ΛR. For the
selected history, take
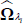 obtained as:
where
obtained as:
where 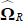 and
and 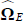 are obtained from
the generated MCMC chain of parameter values during the estimation phase.[25]
are obtained from
the generated MCMC chain of parameter values during the estimation phase.[25] 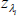 is the
transition variable calculated for the selected history λi.
is the
transition variable calculated for the selected history λi.
-
Cholesky-decompose the estimated variance-covariance matrix
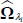 :
and orthogonalise the estimated residuals to get the structural shocks:
:
and orthogonalise the estimated residuals to get the structural shocks:
-
From
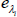 draw with
replacement h eight-dimensional shocks and get the vector of bootstrapped shocks
where h is the horizon for the IRFs we are interested in.
draw with
replacement h eight-dimensional shocks and get the vector of bootstrapped shocks
where h is the horizon for the IRFs we are interested in.
-
Form another set of bootstrapped shocks that will be equal to Equation (A1) except for the
kth shock in
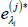 , which is the shock we want to perturb by an
amount equal to δ. Denote the vector of bootstrapped perturbed shocks by
, which is the shock we want to perturb by an
amount equal to δ. Denote the vector of bootstrapped perturbed shocks by 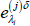 .
.
-
Transform back
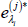 and
and 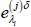 as follows:
and
as follows:
and
-
Use Equations (A2) and (A3) to simulate the evolution of
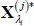 and
and 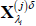 and construct
GIRF(j)(h, δ, λi) as
and construct
GIRF(j)(h, δ, λi) as 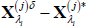 .
.
- Conditional on history λi, repeat for j = 1,…,B vectors of bootstrapped residuals and get GIRF(1) (h, δ, λi), GIRF(2) (h, δ, λi),…,GIRF(B) (h, δ, λi). Set B = 500.
- Calculate the GIRF conditional on history λi as:
-
Repeat all previous steps for i = 1,…, 500 histories belonging to the set of recessionary
histories,
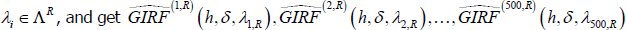 .
.
-
Take the average and get
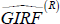 (h, δ,
ΛR), which is the average GIRF under recessions.
(h, δ,
ΛR), which is the average GIRF under recessions.
-
Repeat steps 3 to 12 for 500 histories belonging to the set of all expansions and get
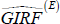 (h, δ, ΛE).
(h, δ, ΛE).
-
The computation of the 68 per cent confidence bands for our impulse responses is undertaken by picking up, per
each horizon of each state, the 16th and the 84th percentile of the densities
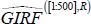 and
and
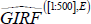 .
.
Footnotes
This section heavily draws on Auerbach and Gorodnichenko's (2012) ‘Appendix: Estimation Procedure’. [23]
The choice p = 12 is due to the number of moving average terms (12) of our transition variable, zt. [24]
We consider the distribution of parameters rather than their mean values to allow for parameter uncertainty, as suggested by Koop et al (1996). [25]