RDP 2016-08: The Slowdown in US Productivity Growth: Breaks and Beliefs 3. Estimation

We estimate the model using Bayesian methods, as is common in the DSGE literature. Our case, however, is non-standard because we allow for structural change and jointly estimate two sets of distinct parameters. These are: (i) the structural parameters of the model, 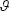, that have continuous support; and (ii) the dates of the structural changes, T = (T_γ, T_b) that have discrete support. The joint posterior density of 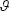and T can be expressed as:

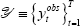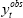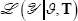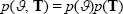where is the data and is an n_obs × 1 vector of observable variables. is the likelihood of the model, which we construct using the methods described in Kulish and Pagan (forthcoming). The priors for the structural parameters and the date breaks are independent, so that . Appendix E describes the posterior sampler.

3.1 Data

We estimate the model using seven series of US quarterly data: GDP, consumption, investment, inflation, the federal funds rate, hours worked, and nominal wages.^[5] GDP, consumption and investment are measured in per capita growth rates, while hours are measured in per capita levels. Appendix A lists the data sources.

Our estimation sample starts in 1964:Q2 and ends in 2014:Q4. From 2008:Q4 to the end of our sample, the federal funds rate was at the zero lower bound. This poses a challenge for our model, which does not allow for nonlinearities in the monetary policy reaction function.

To account for the behaviour of monetary policy at the zero lower bound, from 2008:Q4 to 2014:Q4 we replace the observed federal funds rate with the ‘shadow’ federal funds rate derived by Wu and Xia (2014). This measure quantifies the effective federal funds rate implied by the unconventional monetary policy, such as forward guidance and quantitative easing, undertaken by the Federal Reserve since 2009. For instance, a shadow federal funds rate of −0.5 per cent means that unconventional policy is having the same effect on the US economy as if the Federal Reserve had been able to set the federal funds rate at −0.5 per cent.

An alternative approach would be to incorporate the zero lower bound explicitly in the model and estimation.^[6] This approach has two drawbacks. First, it would complicate the estimation of the model, which seems undesirable as the behaviour of the economy at the zero lower bound is not the focus of this paper. Second, after reaching the zero lower bound, the Federal Reserve continued to apply further monetary stimulus to the US economy through unconventional policy actions. Setting the nominal interest rate to zero without taking account of unconventional policy could lead to incorrect inferences about the behaviour and consequences of US monetary policy over recent years.

3.2 Priors

For the parameters of most interest to us, the growth rate of steady-state TFP in the initial regime, γⁱ, and final regime, γ^f, we impose normal distributions with mean 0.5 and standard deviation 0.2.^[7] The mean of this prior distribution is similar to that used in other estimated US DSGE models, but the standard deviation is wider. Note that our prior is agnostic about the direction of the change in US TFP growth. The estimation is free to conclude that steady-state productivity growth has increased, decreased or stayed the same.

For the parameters governing the timing of the break in steady-state productivity growth, T_γ, and beliefs about the break, T_b, we impose uniform priors. We restrict the domain of these parameters to exclude the first and last 5 per cent of observations. This leaves these parameters with an effective domain of 1966:Q3 to 2012:Q2. This window encompasses all of the date breaks typically identified in single equation reduced form estimation.

For the other parameters, we use the same priors as described in Justiniano et al (2013). Most of these priors are reasonably loose and serve mainly to regularise the posterior distribution of the model so that it remains numerically stable and constrain parameter values to be economically sensible.

Footnotes

The wage series we use is the Bureau of Economic Analysis' (BEA) hourly compensation of employees series. Justiniano et al (2013) use an additional wage series, the Bureau of Labor Statistics' (BLS) average hourly earnings of non-supervisory employees series, in estimation. In Appendix F we explain why we exclude this series. [5]

Examples of estimated DSGE models that take account of the zero lower bound include Kulish, Morley and Robinson (2014) and Jones (2015). [6]

We also experimented with a lower prior mean for γⁱ and γ^f. This modification has almost no effect on our results. [7]