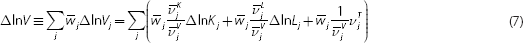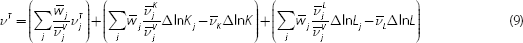RBA Annual Conference – 2016 China's Institutional Impediments to Productivity Growth Harry X Wu[*]
- Download 506KB
1. Introduction
The objective of this paper is to use a productivity approach to understand the institutional problems that may obstruct China's future growth. There have been numerous examples to show that, despite a series of reforms over the past three decades, the government still heavily intervenes in the Chinese economy (Wu, HX 2008). Nonetheless, unlike in the planning period that relied on centralised, comprehensive and mandatory controls through state ownership, local governments have been playing an important role in the reform era under a ‘regionally decentralized authoritarian’ regime (Xu 2011). The driving force is competition among localities over growth. Since local GDP growth is used by upper authorities to assess political performance, local government officials are highly motivated to engage in a growth tournament with their peers in other localities (Li and Zhou 2005). Consequently, their restless search for new growth engines has resulted in increasing government interventions in resource allocation and business decisions (Wu and Shea 2008; Xu 2011; Huang 2012).
There have been several investment waves in which local governments played a very important role. In the 1990s, local governments competed to attract foreign direct investment (FDI). This resulted in huge surplus capacity of labour-intensive manufacturing industries, which was ultimately worked through following China's accession to the World Trade Organization (WTO) in 2001. Second, since the early 2000s, led by coastal provinces, new growth contests began with local urbanisation and industrialisation concentrating on heavy machinery and chemicals (Wu, J 2008). Finally, government dominance in resource allocation was further enhanced in the wake of the global financial crisis in 2008–09 with a CNY4 trillion stimulus package from the central government, accompanied by CNY18 trillion worth of projects funded by various local governments' financing platforms.
The central authorities were caught between two distinct policy choices, with one emphasising the speed of growth and the other underlining the quality of growth. Academics, think-tank economists and the mainstream media have been divided in the debate over the importance of the speed of growth and, hence, the role of government in promoting growth; although both sides criticise the repetitious industrial projects and widespread window-dressing constructions that result from local governments' heavy involvement in resource allocation. Since 2013, the new Xi-Li Administration has appeared willing to allow the market to play a fundamental role in resource allocation and transform the Chinese economy from an input-driven to a more productivity- and innovation-led growth model. This could occur via further structural reforms, albeit still emphasising ‘the dominance of the public ownership’ and ‘the leadership of the state economy’ (CPCCC 2013).
However, what has been missing in the debate is a proper analysis of the sources of growth and productivity trends. The government's heavy involvement has, so far, successfully solved China's growth problem, but it remains unclear to what extent and in which sectors this has taken its toll on the economy's efficiency and productivity. Ultimately, productivity improvements are the key to efficient and sustainable long-run growth in any economy.
To analyse China's productivity performance and the role of government, it is essential to have an industry perspective because government interventions are often made through industry-specific policies. In addition, interventions in upstream industries – those that deliver intermediate goods and services, such as energy and telecommunications – may affect downstream industries through the input-output linkages of the economy. This means that we need a methodological framework that accounts for both the contribution of individual industries to the aggregate productivity performance of the economy and the linkages between them.
The present study benefits from a newly constructed economy-wide industry-level dataset for the Chinese economy that follows the KLEMS principle in data construction.[1] Methodology-wise, this study adopts the Jorgensonian aggregate production possibility frontier (APPF) framework. As an extension, we incorporate the Domar aggregation scheme to account for contributions of individual industries to the growth of aggregate inputs and output (Jorgenson, Ho and Stiroh 2005b). This approach relaxes most of the restrictive assumptions of the widely used aggregate production function approach. That is, that all industries are homogenous with the same value-added function and facing the same input and output prices.
The rest of this paper is organised as follows. Section 2 discusses the role of government in the Chinese economy from an industry perspective. Section 3 introduces the APPF framework, incorporating Domar weights for aggregation. Section 4 briefly introduces the CIP database. This is followed by Section 5, which reports and interprets the empirical results. Finally, Section 6 concludes this study.
2. Sectoral Productivity Growth and the Role of Government
To explore the role of government we may consider distinguishing industries that are subject to different types of government intervention, directly and indirectly through their use of output from regulated industries.
During the reform era, government interventions have become less all-encompassing than they were in the central planning era, when markets were completely ignored. They have become more industry specific through subsidisation or administrative interference, or some combination of both. Subsidies can be made directly or indirectly. Indirect subsidies intend to reduce the producer cost of inputs including energy, land, environment, labour and capital (Huang and Tao 2010). By contrast, direct subsidies come with administrative interferences aiming to compensate for output losses. Administrative interferences serve the state interests or government strategic plans by controlling or influencing output prices and business operations ranging from managerial personnel to the choice of technology.
We argue that whether, or to what extent, the government uses administrative interference or different types of subsidisation depends on the distance of an industry from the final demand, especially the international market. Indirect subsidies have been mainly used by local governments to promote export-oriented manufacturers that make semi-finished and finished goods. Most of these downstream industries are labour intensive and therefore crucial for China to reap its demographic dividend in a timely manner. However, the government tends to directly get involved in upstream industries such as energy and primary input materials that are deemed strategically important in supporting downstream industries (Figure 1).
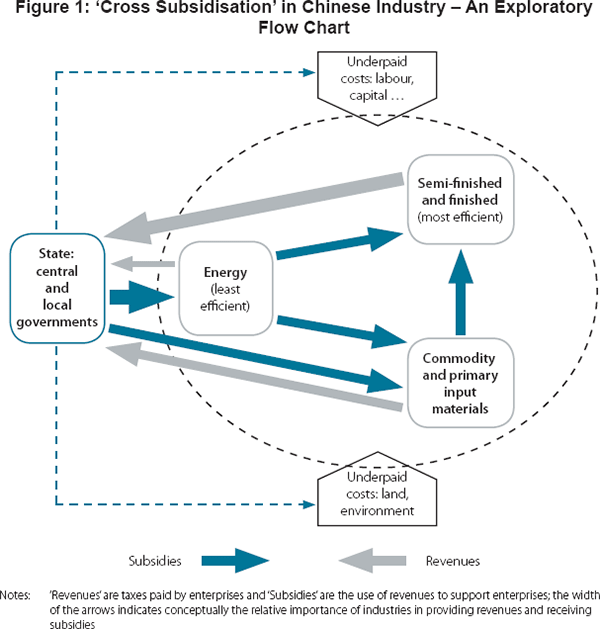
Considering the behaviour of enterprises in such a policy environment, we conjecture that industries that are mainly supported by indirect subsidies could be more efficient and productive than those receiving direct subsidies. In the former case, enterprises may still behave like true market competitors even though their competitiveness is arbitrarily enhanced.[2] Upstream industries are traditionally dominated by state-owned enterprises and do not conform to China's comparative advantage. Their assumed strategic importance gives them strong bargaining power in negotiating for government support. In return they have to accept controls from the authorities. This distorts their behaviour and reduces their incentives to innovate and find efficiency gains.
Figure 1 shows that the nature of the government interventions and subsidies is a kind of ‘cross subsidisation’. The key to sustaining it is that downstream industries must be able to grow faster and relatively more efficiently than upstream industries and the public revenues generated from downstream industries must be able to cover direct subsidies. However, the cost of negative externalities, i.e. the cost that cannot be internalised due to subsidies, has to be borne by the public. Resource misallocation is an additional negative externality that results from government intervention.
To investigate the total factor productivity (TFP) performance of industries we categorise the 37 industries in the CIP database into 8 groups, guided by the degrees of government intervention, either directly or indirectly (see Table 1; details in Table A1).[3] Within the industrial sector, the energy group is monopolised, if not completely owned, by large, central government-owned enterprises due to its strategic importance. It can easily access public resources, but is subject to strong administrative interference. The commodities and primary input materials (C&P) group is also considered important for downstream industries and hence heavily influenced, though not completely owned by the government. Finally, the semi-finished and finished goods (SF&F) group consists of all downstream industries, including not only private enterprises and foreign invested enterprises, but also state-owned enterprises (particularly in heavy machinery industries). However, its competitive nature makes it difficult for the government to directly interfere in business decisions. On average, SF&F is more labour intensive than the other groups, hence more in line with China's comparative advantage. Therefore, we may conjecture that the productivity growth of SF&F is faster than that of energy and C&P. The position of the agricultural and construction industries is less obvious. The agricultural sector not only serves final demand, but also provides intermediate inputs to food processing and manufacturing industries and, as such, can be an important channel for indirect policies. Construction also delivers both investment and consumer goods.
| Sector | Group | Description |
|---|---|---|
| Agricultural | Agriculture | |
| Industrial | Energy | Coal mining, petroleum and utilities |
| Commodities and primary input materials (C&P) | Metals, chemicals and building materials | |
| Semi-finished and finished goods (SF&F) | Wearing apparel, electrical equipment and machinery | |
| Construction | Construction | |
| Services | Services I | State-monopolised services of important intermediate input industries, such as financial intermediaries, transportation, and telecommunication services |
| Services II | Covers market services not included in Services I; these are mainly final demand providers | |
| Services III | Non-market services including government administration, education and healthcare |
3. Accounting for Industry Origin of TFP
The widely used aggregate production function approach to TFP analysis is implicitly subject to very stringent assumptions. First, the value-added functions across industries can only vary by a scalar multiple. Second, there can only be one price for the different types of capital and labour within each industry (Jorgenson et al 2005b). Given heavy government interventions and institutional set-ups that cause market imperfections in China, this approach is inappropriate for the Chinese economy. This study adopts Jorgenson's APPF framework instead, incorporating Domar weights to account for contributions of individual industries to the growth of aggregate inputs and output.
The APPF approach in growth accounting relaxes the strong assumption that all industries are subject to the same value-added production function to account for the industry origin of aggregate growth (Jorgenson 1966). The Domar-weighted aggregation was introduced into the APPF framework in Jorgenson, Gollop and Fraumeni (1987) to exercise direct aggregation across industries to account for the role of American industries in the changes of aggregate inputs. It has been used in Jorgenson and Stiroh (2000) and Jorgenson, Ho and Stiroh (2005a, 2005b) to quantify the role of information technology (IT)-producing and IT-using industries in the US economy. This approach has now become the international standard and has also been applied to the Chinese economy in Cao et al (2009).
To illustrate this methodology, let us begin with a production function where industry gross output is a function of capital, labour, intermediate inputs and technology indexed by time. We use individual industries as building blocks which allow us to explicitly trace the sources of the aggregate productivity growth and input accumulation to the underlying industries. Focusing on an industry-level production function given by Equation (1), each industry, indexed by j, purchases distinct intermediate inputs, capital and labour services to produce a set of products:
where Y is output, K is an index of capital service flows, L is an index of labour service flows, M is an index of intermediate inputs, purchased from domestic industries or imported, and T is the level of TFP. Note that all input variables are indexed by time but this is suppressed for notational convenience.
Under the assumptions of competitive factor markets, full input utilisation and constant returns to scale, the growth of output can be expressed as the cost-weighted growth of inputs and technological change, using the translog functional form:
where  and
and 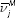 are two-period averages
of nominal weights of input
are two-period averages
of nominal weights of input 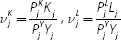 and
and 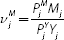 ,
respectively. Note that under constant returns to scale
,
respectively. Note that under constant returns to scale 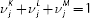 , which
is controlled by industry production accounts in nominal terms. Each element in the
right-hand side of Equation (2) indicates the proportion of output growth accounted for,
respectively, by the growth of capital services
, which
is controlled by industry production accounts in nominal terms. Each element in the
right-hand side of Equation (2) indicates the proportion of output growth accounted for,
respectively, by the growth of capital services 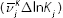 , labour
services
, labour
services 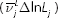 , intermediate materials
, intermediate materials 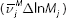 and TFP
and TFP 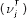 .
.
One of the advantages of Equation (2) is that it can better account for the quality of inputs. For example, it can account for labour services provided by different types of labour with specific demographic, educational and industrial attributes, as shown in pioneering studies by Griliches (1960), Denison (1962) and Jorgenson and Griliches (1967). It has relaxed the usual strong assumption that treats numbers employed or hours worked as a homogenous measure of labour input. The growth of total labour input is thus defined as a Törnqvist quantity index of individual labour types as follows:
where ΔlnHh,j indicates the growth of hours worked by each labour
type h (with specific gender, age and educational attainment) and its cost weights
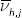 given by two-period average shares of each type in the nominal value of labour compensation
controlled by the labour income of industry production accounts.
given by two-period average shares of each type in the nominal value of labour compensation
controlled by the labour income of industry production accounts.
The same user-cost approach is also applied to K and M to account for the
contribution of different types of capital assets (Zk) and intermediate
inputs (Mm) in production with type-specific, two-period average cost
weights defined as 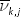 and
and 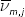 ,
respectively:
,
respectively:
It should be noted that the equations from (2) through the whole set of (3) also explicitly express the methodological framework for the CIP industry-level data construction that is linked to, and controlled by, the national production and income accounts. This point will be discussed again when we discuss the data issues in the following section.
Using the value added concept, Equation (2) can be rewritten as:
where Vj is the real value added in j and 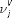 is the nominal share of value added in industry gross output.
is the nominal share of value added in industry gross output.
By rearranging Equations (2) and (4), we can obtain an expression for the sources of industry value-added growth (i.e. measured in terms of input contributions):
Growth of aggregate value added by the APPF approach is expressed as weighted industry value added in a Törnqvist index:
where wj is the share of industry value added in aggregate value added. By combining Equations (5) and (6), we can have a new expression of aggregate value-added growth by weighted contribution of industry capital growth, industry labour growth and TFP growth:
Through this new expression, we have introduced the well-known Domar weights in our
aggregation (Domar 1961), that is, a ratio of each industry's share in total value added
(wj) to the proportion of the industry's value added in its gross
output 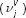 .
.
If we maintain the stringent assumption that capital and labour inputs have the same marginal productivity in all industries we can define aggregate TFP growth as:
However, this assumption is unlikely to hold, especially in China, as argued above. It is therefore interesting to look at the difference of the two measurement approaches. By subtracting Equation (7) from Equation (8) and rearranging, we can show how the aggregate TFP growth relates to the sources of TFP growth at the industry level and to the effect of factor mobility across industries (Jorgenson et al 2005b):
in which the reallocation terms in the second and third brackets can be simplified as:
Equation (9) expresses the aggregate TFP growth in terms of three sources: Domar-weighted
industry TFP growth, reallocation of capital and reallocation of labour across industries.
This Domar weighting scheme 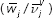 , originated by Domar (1961), plays
a key role in the direct aggregation across industries under the Jorgensonian growth
accounting framework. A direct consequence of the Domar aggregation is that the weights do
not sum to unity, implying that aggregate productivity growth amounts to more than the
weighted average of industry-level productivity growth (or less, if negative). This reflects
the fact that productivity change in the production of intermediate inputs do not
only have an ‘own’ effect, but, in addition, they lead to reduced or increased
prices in downstream industries, and that effect accumulates through vertical links. As
elaborated by Hulten (1978), the Domar aggregation establishes a consistent link between
industry-level productivity growth and the aggregate productivity growth. Productivity gains
of the aggregate economy may exceed the average productivity gains across industries because
flows of intermediate inputs between industries contribute to aggregate productivity by
allowing productivity gains in successive industries to augment one another. The same logic
can explain productivity losses.
, originated by Domar (1961), plays
a key role in the direct aggregation across industries under the Jorgensonian growth
accounting framework. A direct consequence of the Domar aggregation is that the weights do
not sum to unity, implying that aggregate productivity growth amounts to more than the
weighted average of industry-level productivity growth (or less, if negative). This reflects
the fact that productivity change in the production of intermediate inputs do not
only have an ‘own’ effect, but, in addition, they lead to reduced or increased
prices in downstream industries, and that effect accumulates through vertical links. As
elaborated by Hulten (1978), the Domar aggregation establishes a consistent link between
industry-level productivity growth and the aggregate productivity growth. Productivity gains
of the aggregate economy may exceed the average productivity gains across industries because
flows of intermediate inputs between industries contribute to aggregate productivity by
allowing productivity gains in successive industries to augment one another. The same logic
can explain productivity losses.
The next two terms reflect the effect on aggregate TFP growth of the reallocation effect of capital (ρK) and labour (ρL) across industries, respectively. Each of the reallocation terms is obtained by subtracting cost-weighted aggregate factor (capital or labour) input growth from the Domar-weighted input growth across industries. It should be noted that both theoretically and methodologically, when these terms are not negligible, it indicates that industries do not face the same factor costs, which suggests a violation of the assumption of the widely used aggregate approach. One should not expect a significant reallocation effect in an economy where there is a well-developed market system. However, this is a very useful analytical tool for the Chinese case where strong government interventions in resource allocation may have caused severe market distortions.
4. Data and Periodisation
4.1 Data
This study has uniquely benefited from a newly constructed economy-wide, industry-level dataset in the ongoing CIP project. It is beyond the scope of this study to go through a long history of separate database studies.[4] We refer the interested reader to three working papers (Wu 2015; Wu and Ito 2015; Wu, Yue and Zhang 2015), as well as earlier versions of this work if one wants to trace the development of the data construction ideas (e.g. Wu and Xu 2002; Wu and Yue 2003, 2010, 2012; Wu, HX 2008).
In the CIP project, the principles of industry data construction adhere to the underlying theory and data constraints as expressed in Equation (2) and the set of Equations (3a), (3b) and (3c). This implies that the industry-level data are linked to, and made consistent with, the national production and income accounts of China.
Some features of the CIP data should be noted. The classification of industries, in principle, adopts the 2002 version of the Chinese Standard Industrial Classification (CSIC/2002) and reclassifies the economy into 37 industries (see Table A1). The reconstruction of the Chinese national accounts is based on different versions of official national accounts compiled under the Material Product System (MPS) prior to 1992 and the United Nations System of National Accounts (SNA) afterwards. China's SNA input-output accounts, that are available every five years since 1987, and a MPS input-output table for 1981, that is converted to a SNA-type table, are used to construct a time series of Chinese input-output accounts for the period 1981–2010 (Wu and Ito 2015). It should be noted that in constructing industry accounts we are not able to challenge the official national accounts data except for consistency adjustment (concept, coverage and classification). Nonetheless, the widely discussed data problems observed at a macro or aggregate level should be borne in mind when interpreting our industry-weighted results for the aggregations.[5]
The nominal accounts are deflated by industry-level producer price indices (PPI), constructed using official PPIs for the agricultural and industrial sectors, and the consumer price index or its components for service industries (Wu and Ito 2015). However, the work reported in this paper uses the single deflation approach, assuming changes in input prices are the same as changes in output prices, similar to the Chinese national accounts. A double-deflation approach would have been preferred, but cannot be used due to a lack of price data.[6]
For the required labour data, following earlier studies by Wu and Yue (2003, 2010, 2012) which analysed the industrial sector only, CIP has established economy-wide employment series (in both numbers of workers employed and hours worked) and compensation matrices for 37 industries. Workers include both employees and self-employed workers (farming households and self-employed retailers and transporters), cross-classified by gender, seven age groups and five educational levels (see details in Wu et al (2015)).
The construction of net capital stock at the industry level proved most challenging. CIP has reconstructed annual flows of investment for the industrial sector groups using official gross capital stock data at historical costs. However, CIP uses the official investment series estimates for the non-industrial sectors. The results are yet to be reconciled with the national accounts gross fixed capital formation data. Industry-specific investment deflators are constructed using the PPIs of investment goods industries and the nominal wage index of construction workers (Wu, HX 2008, 2015). The industry-specific depreciation rates are estimated based on asset service lives and declining balance values used in the US national accounts, following the approach developed by Hulten and Wykoff (1981).
4.2 Periodisation
To better examine the effect on productivity of major policy regime shifts, we divide the entire period covered by the current version of the CIP data, 1980–2012, into four sub-periods, namely: 1980–91, 1992–2001, 2002–07 and 2008–12. In most cases, the empirical findings are reported in line with this periodisation. The first sub-period (1980–91) is characterised by de-collectivisation in agriculture and reform in the industrial sector to introduce market pricing.
The second sub-period (1992–2001) began with Deng's call for bolder and deeper reforms in 1992 and the official adoption of the so-called ‘socialist market economy’ in 1993. Wider opening up to Western technology and FDI drove a new wave of investment in export-oriented manufacturing. Meanwhile, due to deregulation of private activities, new private firms absorbed a huge number of the state industrial employees who lost their jobs in the state-owned enterprise reforms of the 1990s. However, it also resulted in serious overinvestment. The Asian financial crisis (1997–98) hit the Chinese economy hard, and from 1998 China entered a four-year-long deflation period.[7]
The third sub-period (2002–07) begins shortly after China's WTO entry at the end of 2001. It is characterised by counteracting forces. On one hand, WTO entry induced a further opening up to foreign trade and direct investment. This pushed the Chinese economy further towards the market system. On the other hand, consolidated and enlarged state corporations resurged in the name of protecting national interests in a time of accelerating globalisation. Meanwhile, growth-motivated local governments were pressured to race for rapid urbanisation and heavy industrialisation.
We treat the period 2008–12 as the last sub-period to examine the aftermath of the global financial crisis. The unprecedented fiscal stimulus package from both the central and local governments substantially enhanced the role of state-owned enterprises (SOEs).
5. Empirical Results
5.1 Sources of gross output growth by industry group
We start with an examination of industry-level sources of gross output growth based on the production function expressed in Equation (2) (Table 2; Figure 2). This is a necessary starting point because industries are building blocks of the national economy and the originators of the aggregate productivity growth.
| Gross output | L | K | M | TFP | |
|---|---|---|---|---|---|
| 1980–91 | |||||
| Agriculture | 6.7 | 0.8 | 1.0 | 2.8 | 2.2 |
| Energy | 0.9 | 0.5 | 3.5 | 1.9 | −5.0 |
| C&P | 7.9 | 0.4 | 2.4 | 5.9 | −0.9 |
| SF&F | 13.5 | 0.2 | 2.1 | 9.9 | 1.3 |
| Construction | 7.4 | 2.0 | 0.6 | 5.1 | −0.3 |
| Services I | 10.9 | 0.9 | 6.0 | 3.3 | 0.7 |
| Services II | 10.6 | 1.5 | 2.7 | 5.2 | 1.2 |
| Services III | 5.5 | 1.8 | 1.2 | 1.9 | 0.7 |
| 1992–2001 | |||||
| Agriculture | 7.3 | 0.6 | 0.7 | 3.5 | 2.4 |
| Energy | 7.0 | −0.1 | 3.4 | 4.7 | −1.0 |
| C&P | 11.0 | −0.1 | 1.5 | 8.0 | 1.6 |
| SF&F | 14.2 | 0.1 | 1.6 | 10.4 | 2.1 |
| Construction | 12.5 | 1.1 | 1.4 | 9.3 | 0.7 |
| Services I | 7.1 | 0.6 | 6.3 | 3.9 | −3.6 |
| Services II | 9.4 | 1.5 | 6.1 | 4.4 | −2.7 |
| Services III | 9.1 | 2.4 | 1.0 | 5.4 | 0.3 |
| 2002–07 | |||||
| Agriculture | 3.7 | −2.4 | 0.8 | 1.4 | 3.9 |
| Energy | 15.0 | 0.7 | 3.2 | 11.7 | −0.5 |
| C&P | 15.2 | 0.4 | 2.1 | 12.3 | 0.4 |
| SF&F | 17.9 | 0.7 | 2.2 | 14.4 | 0.6 |
| Construction | 13.7 | 0.3 | 1.4 | 10.7 | 1.2 |
| Services I | 12.1 | 1.1 | 4.9 | 5.9 | 0.2 |
| Services II | 10.5 | 1.3 | 6.9 | 4.3 | −2.1 |
| Services III | 11.4 | 4.5 | 2.6 | 4.8 | −0.5 |
| 2008–12 | |||||
| Agriculture | 4.4 | −1.9 | 0.5 | 1.9 | 3.8 |
| Energy | 4.2 | 0.3 | 2.4 | 2.9 | −1.5 |
| C&P | 13.0 | 0.1 | 2.3 | 10.9 | −0.3 |
| SF&F | 13.9 | 0.2 | 2.2 | 11.7 | −0.2 |
| Construction | 8.2 | 1.1 | 1.8 | 5.1 | 0.2 |
| Services I | 14.0 | 1.4 | 4.6 | 8.6 | −0.6 |
| Services II | 9.8 | 0.7 | 7.6 | 2.8 | −1.4 |
| Services III | 3.7 | 7.8 | 1.8 | −2.1 | −3.8 |
|
Source: Based on Equation (2) using CIP 2.2 data |
|||||
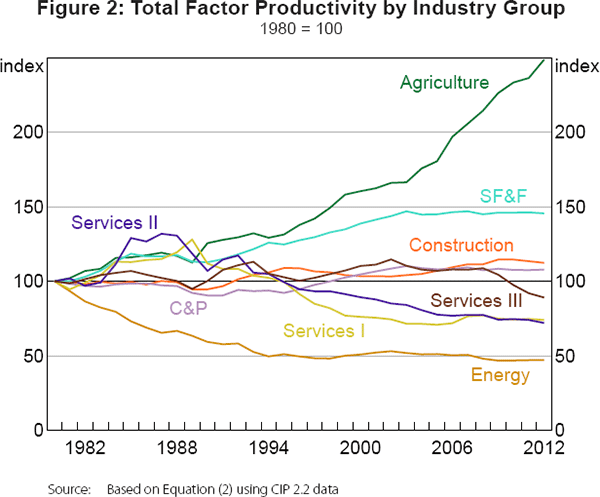
China's agricultural sector achieved the best TFP performance of all groups. It maintained strong positive productivity growth throughout the three decades and has had the fastest TFP growth since the 2000s. This was accompanied by a rapid decline in labour input in the more recent periods. In assessing agricultural performance, three factors should be considered. First, although agriculture still received various subsidies in the 2000s, unlike in the planning era, the sector was no longer subject to administrative controls. Second, we adopt the official broad measure of labour compensation that defines the income of the self-employed (including all farmers) as labour income rather than capital income, as suggested by SNA. Third, we are not yet able to measure the contribution by land.[8]
The SF&F and C&P groups are well known as China's growth engines and the backbone of the world's factory. Compared to C&P, as discussed earlier, SF&F received much less direct government interference due to its competitive nature and greater exposure to the international market. As expected, we find that SF&F in general experienced faster productivity growth than C&P. Before the global financial crisis, despite significant increases in input materials, both groups showed positive TFP growth, except for C&P in the 1980s. In the wake of the crisis, both suffered from TFP decline.
The performance of the energy group presents a sharp contrast to the SF&F group. It experienced heavy TFP loss in the 1980s and has not been able to get back to its 1980 level of TFP. This may not be a big surprise because this group consists of industries almost completely monopolised by SOEs and subject to heavy government interventions.[9]
Since the 1990s, China's construction industry has maintained positive, though slow, TFP growth, which is not often observed in other economies. Most market services (I and II) show exceptional acceleration of TFP growth in the 1980s following deregulation after a long period of suppressed service development under central planning. However, it has to be acknowledged that these estimates are only preliminary; overestimation of output and underestimation of output prices due to the political incentives of local governments have led to major measurement problems and complicate productivity measurement in services. Compared to Services II (market), there are more state subsidies and administrative controls in Services I (market monopolies) and III (non-market and ‘non-material’, see Wu (2014)). These factors could be translated into different TFP growth rates, but are not easily disentangled. TFP in Services I and II has been declining since the late 1980s, whereas Services III have experienced nearly zero TFP growth on average.
5.2 Sources of value-added growth in the APPF framework
From the above analysis, we have seen that the growth of factors and productivity vary between industries over time. In this sub-section we examine China's aggregate TFP performance in the APPF framework, taking into account that industries (groups) may have different value-added functions (Table 3).
| 1980–91 | 1992–2001 | 2002–07 | 2008–12 | 1980–2012 | |
|---|---|---|---|---|---|
| Industry contributions | |||||
| Value-added growth due to: | 7.61 | 9.04 | 11.00 | 9.23 | 8.94 |
| Agriculture | 1.75 | 1.18 | 0.50 | 0.65 | 1.17 |
| Energy | −0.06 | 0.33 | 0.74 | 0.30 | 0.27 |
| C&P | 0.90 | 1.49 | 1.57 | 1.31 | 1.28 |
| SF&F | 1.87 | 2.65 | 2.72 | 2.01 | 2.29 |
| Construction | 0.38 | 0.64 | 0.68 | 0.73 | 0.58 |
| Services I | 0.92 | 0.64 | 1.47 | 1.20 | 0.98 |
| Services II | 1.45 | 1.74 | 2.39 | 2.35 | 1.86 |
| Services III | 0.39 | 0.37 | 0.94 | 0.67 | 0.53 |
| Factor contributions | |||||
| Value-added growth due to: | 7.61 | 9.04 | 11.00 | 9.23 | 8.94 |
| Capital input | 5.00 | 6.15 | 8.63 | 9.30 | 6.71 |
| Stock | 5.00 | 6.22 | 8.71 | 9.30 | 6.75 |
| Capital quality (composition) | −0.01 | −0.07 | −0.08 | 0.00 | −0.04 |
| Labour input | 1.39 | 1.26 | 1.19 | 1.98 | 1.40 |
| Hours | 1.34 | 0.88 | 0.71 | 0.34 | 0.92 |
| Labour quality (composition) | 0.05 | 0.38 | 0.48 | 1.65 | 0.48 |
| Aggregate TFP | 1.22 | 1.63 | 1.19 | −2.06 | 0.83 |
These estimates suggest the Chinese economy achieved average real output growth of 8.94 per cent per annum in 1980–2012. The SF&F group was the top growth contributor before the global financial crisis. In the wake of the crisis, productivity growth in Services II was marginally higher than in SF&F. On average over 1980–2012, SF&F contributed around one quarter of the real output growth, Services II contributed 20 per cent, and agriculture, C&P and Services I together contributed nearly 40 per cent.
The estimated aggregate TFP growth is 0.83 per cent per annum on average. However, TFP performance was highly unstable over time with the highest growth achieved in 1992–2001 (1.63) and the worst in 2008–12 (−2.06).[10]
Of the 8.94 per cent annual output growth rate over the period examined, 75 per cent relied on capital input, 16 per cent on labour input and 9 per cent on TFP growth. The contribution of capital input increased from 66 per cent in the 1980s to 78 per cent post-WTO accession and around 100 per cent in the wake of the global financial crisis. On the other hand, the contribution of labour input declined from 18 per cent in the 1980s to 11 per cent post-WTO accession. This trend reversed following the crisis and the contribution of labour input rose back to 21 per cent, which was largely due to quality improvement rather than hours worked. The contribution of the quality of capital was insignificant on average.[11]
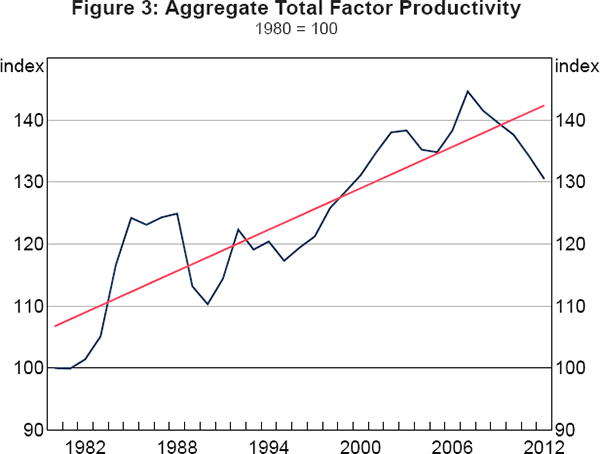
When annual aggregate TFP growth rates are translated into a level index, we observe a volatile TFP performance around its underlying trend (Figure 3). The first TFP drive was clearly observed in the early 1980s, which was associated with China's agricultural reform. As a result, the Chinese productivity performance stayed well above the trend until its collapse following the 1989 political crisis. TFP growth recovered in the early 1990s, but this was only short lived. It began to accelerate again from the late 1990s and exceeded the trend in the early 2000s. In the post-WTO accession period, the resurgence of a fast TFP growth was only observed in 2006–07 before its sharp drop in the wake of the global financial crisis. The most recent significant slowdown in the official GDP growth rate from above 10 per cent in 2010 to below 7 per cent per year in 2015 seems to suggest that China is facing serious challenges in generating positive productivity growth.
China's aggregate value added can be decomposed into hours worked and value added per hour worked, with the latter reflecting productivity improvements from capital deepening, labour quality and TFP (Table 4). The economy has benefited significantly from the increase in hours worked, which has been referred to as China's ‘demographic dividend’. However, the boost from this has declined over time from 2.83 per cent per annum in 1980–91 to 0.73 per cent per annum in 2008–12. Although value added per hour worked has increased, this appears to have been increasingly dependent on capital deepening. More importantly, the growth of labour productivity was not necessarily in line with the pace of capital deepening when comparing the results for 2008–12 with those for 2002–07. This suggests serious disequilibrium and misallocation of resources that was likely caused by increasing overinvestment.
| 1980–91 | 1992–2001 | 2002–07 | 2008–12 | 1980–2012 | |
|---|---|---|---|---|---|
| Growth rates | |||||
| Value-added growth | 7.61 | 9.04 | 11.00 | 9.23 | 8.94 |
| Value added per hour worked | 4.78 | 7.29 | 9.44 | 8.50 | 7.02 |
| Hours | 2.83 | 1.75 | 1.57 | 0.73 | 1.93 |
| Factor contributions | |||||
| Value added per hour worked | 4.78 | 7.29 | 9.44 | 8.50 | 7.02 |
| Capital deepening | 3.51 | 5.28 | 7.77 | 8.91 | 5.71 |
| Labour quality (composition) | 0.05 | 0.38 | 0.48 | 1.65 | 0.48 |
| Aggregate TFP | 1.22 | 1.63 | 1.19 | −2.06 | 0.83 |
5.3 The industry origin of aggregate TFP growth
In order to explicitly account for differences across industries and their effect on China's aggregate TFP performance, we now introduce Domar weights in the exercise, following the studies on the US economy by Jorgenson et al (2005a, 2005b). The results presented in the first line of Table 5 are estimated with the stringent assumption that marginal productivities of capital and labour are the same across all industries, which are the same as those presented in Tables 3 and 4. As expressed in Equation (9), using Domar weights, the aggregate TFP growth rate can be decomposed into three additive components: 1) the change of Domar-weighted aggregate TFP; 2) the change of capital reallocation; and 3) the change of labour reallocation. On average over the entire period 1980–2012, China's TFP growth estimated with the Domar weights is 0.52 per cent per annum, much slower than the aggregate TFP growth of 0.83 percentage points, implying a net factor reallocation effect of 0.31, which will be discussed later. The highest contributor to the Domar-weighted aggregate TFP growth was agriculture, which contributed 0.83 percentage points. The SF&F group also did rather well over time (0.57), as did construction (0.08). The worst performer was the energy group (−0.47), followed by Services II (−0.33) and Services III (−0.18). Such a sharp contrast across industry groups in TFP performance can also be observed over different sub-periods, which clearly suggests that treating individual industries as homogenous in the growth accounting can substantially distort our view of the productivity performance of the Chinese economy.
| 1980–91 | 1992–2001 | 2002–07 | 2008–12 | 1980–2012 | |
|---|---|---|---|---|---|
| Aggregate TFP growth | 1.22 | 1.63 | 1.19 | −2.06 | 0.83 |
| Domar-weighted TFP growth | 0.60 | 1.72 | 0.54 | −2.10 | 0.52 |
| Agriculture | 0.99 | 0.75 | 0.82 | 0.68 | 0.83 |
| Energy | −0.76 | −0.24 | −0.32 | −0.49 | −0.47 |
| C&P | −0.50 | 0.77 | 0.20 | −0.27 | 0.07 |
| SF&F | 0.30 | 1.35 | 0.50 | −0.35 | 0.57 |
| Construction | −0.05 | 0.12 | 0.29 | 0.04 | 0.08 |
| Services I | 0.25 | −0.59 | 0.28 | −0.02 | −0.05 |
| Services II | 0.31 | −0.42 | −0.79 | −0.97 | −0.33 |
| Services III | 0.06 | −0.03 | −0.43 | −0.71 | −0.18 |
| Reallocation of K (ρK) | 0.28 | −0.09 | −1.03 | −0.01 | −0.12 |
| Reallocation of L (ρL) | 0.35 | 0.01 | 1.68 | 0.06 | 0.44 |
|
Source: Based on Equation (9) using CIP 2.2 data |
|||||
A closer examination through sub-periods with the background of the policy regime shifts that took place may shed important light on the role of the government. The agricultural sector benefited most from reforms in the 1980s, especially the decollectivisation of farming and deregulation of rural township–village enterprises. Even in the latest period that was affected by the global financial crisis, agriculture was the most important contributor to the Domar-weighted TFP growth, which might come as a big surprise. While its share in nominal GDP was declining over time, its contribution to the Domar-weighted TFP growth remained high throughout the period. This is suggestive of a process in which the agricultural sector is still releasing capital (including land) and labour that have a marginal productivity below the sector's average. By shedding these surplus factors, the average productivity of the remaining factors is growing. But clearly this cannot be a long-run source of growth as this structural shift is temporary. Future growth must come from the manufacturing and services sectors.[12]
The most rapid TFP growth occurred in the period 1992–2001, at 1.72 per cent per annum using the Domar weights, despite the effect of the Asian financial crisis (1997–98) and the subsequent deflation in 1998–2003. The SF&F group was the most important contributor, followed by the C&P group, thanks to unprecedented state sector reforms and opening up to foreign trade and direct investment, which allowed the market to play an increasing role in resource allocation. The productivity performance of the construction industry also turned positive and the productivity decline of the energy group slowed.
Nevertheless, we find that China's accession to the WTO at the end of 2001 was accompanied by a slowdown, rather than an acceleration of TFP growth. This puzzling result may be partly reflecting the increased interventions by local governments throughout the 2000s, which aimed at promoting local urbanisation and heavy industrialisation (Wu, HX 2008). While the contribution of SF&F and C&P to TFP growth declined considerably between 2001 and 2007, the contribution of construction and state-monopolised Services I (transportation, telecommunication and financial services), increased significantly.
In the wake of the global financial crisis, and a large amount of stimulus from the central and local governments, China's Domar-weighted TFP growth turned to negative, declining by −2.10 per cent per annum. Since most of the projects concentrated on infrastructure development, construction continued to benefit though with nearly zero TFP growth. For the same reason, TFP in Services I did not decline as rapidly as in other sectors. Since 2012, the effect of the unprecedented government injection has likely abated, although there are increasing signs indicating that China's surplus capacity in manufacturing is worsening and may take many years to solve.
5.4 The effect of factor reallocation
The slower Domar-weighted TFP growth (0.52) compared to the aggregate TFP growth (0.83) implies that around 60 per cent of the aggregate TFP growth is attributable to the productivity performances within individual industries and around 40 per cent is due to the reallocation of capital and labour. This reflects a positive labour reallocation effect (ρL) of 0.44 percentage points, which more than offsets a negative capital reallocation effect (ρK) of −0.12 percentage points (Table 5; Figure 4).
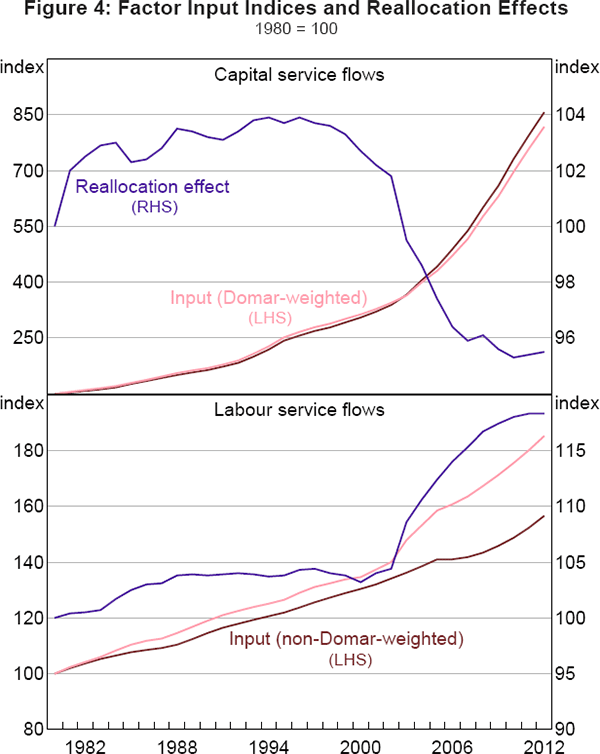
It should be noted that such a magnitude of reallocation effect is typically not observed in market economies. For example, based on their empirical work on the US economy from 1977–2000, Jorgenson et al (2005b) showed that the reallocation effect was generally negligible. For the sub-periods where the reallocation effect was non-negligible, the capital and labour reallocation effects generally moved in the opposite direction to each other. Jorgenson et al (1987) also reported that the reallocation of capital was typically positive and the reallocation of labour was typically negative for the US economy for the period 1948–79. This is because capital grew more rapidly in industries with high capital service prices, hence high returns on capital, whereas labour grew relatively slowly in industries with high marginal compensation.
In the case of China, the much larger magnitude and unexpected sign of capital and labour reallocation effects have two important implications. First, individual industries indeed face significantly different marginal factor productivities, suggesting that there are barriers to factor mobility which cause misallocation of resources in the economy. The flip side of this finding is that corrections to the distortions can potentially be productivity enhancing, which might be good news in terms of the much-talked-about and long-awaited structural reforms.
We find that the effect of labour reallocation remained generally positive over time. This may suggest that reforms improved the efficiency of the labour market. But this is not the case for the capital market. Notably, the most significant gain from labour reallocation was experienced during the post-WTO accession period, which may have been driven by the rapid expansion of export-oriented, labour-intensive industries that was in line with China's comparative advantage.
The case of capital reallocation is different. The early reform period was the only period that saw a positive effect of capital reallocation, possibly due to partial removal of the distortions inherited from the central planning period. However, the effect turned negative following China's WTO entry, likely because of the enhanced role of the government that supported the state sector resurging in upstream industries.
Nevertheless, the results for the post-crisis period (2008–12) deserve greater attention. During this period, the reallocation effect in both capital and labour became close to zero, a distinct contrast to the earlier periods. This rather unusual observation likely reflects the government's efforts to keep the economy insulated from the external shock. If this finding is true, the unprecedented government stimulus package did not change the structure of the economy in terms of resource allocation.
6. Concluding Remarks
Using the newly constructed CIP database this study examines the industry sources of growth in the Chinese economy for the reform period 1980–2012, based on the aggregate production possibility frontier approach in the Jorgensonian growth accounting framework. As an extension, we used the Domar aggregation approach to separately identify the within-industry productivity changes and the productivity changes due to labour and capital reallocation.
Our preliminary results show that China achieved a TFP growth of 0.83 per cent per annum for the entire period 1980–2012. This means that TFP growth accounted for about 9.3 per cent of the 8.94 per cent per annum growth of industry-weighted value added. This result is much smaller than all previous productivity studies on the Chinese economy based on the aggregate approach. For example, Bosworth and Collins (2008) and Perkins and Rawski (2008) estimated that TFP accounted for around 40 per cent of GDP growth. Compared to the only work in the literature that applied the same approach for the period 1982–2000, our finding is about one-third of their result (Cao et al 2009). The differences could come from data construction, measurement, classification or coverage (for example, we have 11 services sectors whereas Cao et al had 1 services sector).
At the industry group level, we do find that, in general, industries less prone to government intervention, such as agriculture and the SF&F manufactures, tended to have higher TFP growth rates than those industries subjected to direct government interventions, such as the energy group. The fact that the SF&F group maintained a positive TFP growth while the energy group experienced persistent TFP declines suggests the existence of cross-subsidisation between upstream and downstream industries, in which the government plays different roles to serve its strategy.
We also found strong effects of factor input reallocation across industries, which significantly address the key issue of resource misallocation in the ongoing policy debate. The large magnitude of the reallocation effect on the one hand reflects barriers to factor mobility in the economy and on the other hand also suggests potential gain from market-driven reallocation. Institutional deficiencies in the Chinese economy that allow governments at all levels to affect resource allocation at their discretion are responsible for resource misallocation. Therefore, disentangling government from business and allowing the market to correct the cost structure of industries is the key to solving China's structural problems. Indeed, restructuring for healthy and sustainable growth is the most crucial and challenging pillar of Liconomics. Nevertheless, there is no such thing as the ‘right structure’ without allowing more market-based resource allocation across industries.
Appendix A: Data
| CIP code | EU-KLEMS code | Grouping | Industry | |
|---|---|---|---|---|
| 1 | AtB | Agriculture | Agriculture, forestry, animal husbandry and fishery | AGR |
| 2 | 10 | Energy | Coal mining | CLM |
| 3 | 11 | Energy | Oil and gas excavation | PTM |
| 4 | 13 | C&P | Metal mining | MEM |
| 5 | 14 | C&P | Non-metallic minerals mining | NMM |
| 6 | 15 | SF&F | Food and kindred products | F&B |
| 7 | 16 | SF&F | Tobacco products | TBC |
| 8 | 17 | C&P | Textile mill products | TEX |
| 9 | 18 | SF&F | Apparel and other textile products | WEA |
| 10 | 19 | SF&F | Leather and leather products | LEA |
| 11 | 20 | SF&F | Sawmill products, furniture and fixtures | W&F |
| 12 | 21t22 | C&P | Paper products, printing and publishing | P&P |
| 13 | 23 | Energy | Petroleum and coal products | PET |
| 14 | 24 | C&P | Chemicals and allied products | CHE |
| 15 | 25 | SF&F | Rubber and plastics products | R&P |
| 16 | 26 | C&P | Stone, clay and glass products | BUI |
| 17 | 27t28 | C&P | Primary and fabricated metal industries | MET |
| 18 | 27t28 | SF&F | Metal products (excluding rolling products) | MEP |
| 19 | 29 | SF&F | Industrial machinery and equipment | MCH |
| 20 | 31 | SF&F | Electric equipment | ELE |
| 21 | 32 | SF&F | Electronic and telecommunication equipment | ICT |
| 22 | 30t33 | SF&F | Instruments and office equipment | INS |
| 23 | 34t35 | SF&F | Motor vehicles and other transportation equipment | TRS |
| 24 | 36t37 | SF&F | Miscellaneous manufacturing industries | OTH |
| 25 | E | Energy | Power, steam, gas and tap water supply | UTL |
| 26 | F | Construction | Construction | CON |
| 27 | G | Services II | Wholesale and retail trade | SAL |
| 28 | H | Services II | Hotels and restaurants | HOT |
| 29 | I | Services I | Transport, storage and post services | T&S |
| 30 | 71t74 | Services I | Telecommunication and post | P&T |
| 31 | J | Services I | Financial intermediation | FIN |
| 32 | K | Services II | Real estate services | REA |
| 33 | 71t74 | Services II | Leasing, technical, science and business services | BUS |
| 34 | L | Services III | Public administration and defence | ADM |
| 35 | M | Services III | Education services | EDU |
| 36 | N | Services III | Health and social security services | HEA |
| 37 | O&P | Services II | Other services | SER |
|
Notes: This is based on Wu's series of works to reclassify official statistics reported under different CSIC systems adopted in CSIC/1972, CSIC/1985 and CSIC/1994 (Wu and Yue 2012; Wu and Ito 2015); the current Chinese classification system CSIC/2011 largely conforms to the 2-digit level industries of the ISIC (rev 4) and can be reconciled with the EU-KLEMS system of classification (Timmer et al 2007) |
||||
| Value added | Total factor productivity | |||||
|---|---|---|---|---|---|---|
| Weight | Growth | Contribution to growth | Domar weight | Growth | Contribution to growth | |
| AGR | 0.197 | 5.32 | 1.17 | 0.310 | 2.85 | 0.83 |
| CLM | 0.016 | 7.55 | 0.12 | 0.032 | 1.02 | 0.02 |
| PTM | 0.018 | −2.65 | −0.04 | 0.026 | −9.79 | −0.25 |
| MEM | 0.005 | 10.99 | 0.06 | 0.014 | 1.19 | 0.01 |
| NMM | 0.006 | 9.38 | 0.05 | 0.013 | 2.07 | 0.03 |
| F&B | 0.027 | 10.84 | 0.29 | 0.126 | 0.22 | 0.02 |
| TBC | 0.012 | 7.97 | 0.09 | 0.018 | −4.79 | −0.11 |
| TEX | 0.026 | 7.38 | 0.19 | 0.110 | −0.04 | −0.03 |
| WEA | 0.009 | 12.60 | 0.11 | 0.035 | 0.67 | 0.03 |
| LEA | 0.004 | 11.40 | 0.05 | 0.020 | 0.43 | 0.01 |
| W&F | 0.007 | 12.61 | 0.09 | 0.026 | 1.12 | 0.03 |
| P&P | 0.011 | 10.09 | 0.12 | 0.039 | 0.46 | 0.02 |
| PET | 0.011 | 0.14 | −0.01 | 0.043 | −3.92 | −0.14 |
| CHE | 0.036 | 10.58 | 0.38 | 0.134 | 0.42 | 0.05 |
| R&P | 0.012 | 12.10 | 0.14 | 0.048 | 0.61 | 0.03 |
| BUI | 0.025 | 9.50 | 0.23 | 0.077 | 0.43 | 0.04 |
| MET | 0.032 | 7.83 | 0.24 | 0.135 | −0.47 | −0.07 |
| MEP | 0.012 | 12.09 | 0.15 | 0.050 | 0.97 | 0.04 |
| MCH | 0.035 | 10.96 | 0.38 | 0.119 | 1.76 | 0.19 |
| ELE | 0.015 | 13.99 | 0.20 | 0.065 | 0.78 | 0.04 |
| ICT | 0.015 | 16.55 | 0.23 | 0.075 | 1.14 | 0.02 |
| INS | 0.003 | 17.91 | 0.05 | 0.009 | 3.60 | 0.03 |
| TRS | 0.018 | 16.27 | 0.29 | 0.074 | 2.12 | 0.12 |
| OTH | 0.015 | 15.10 | 0.22 | 0.043 | 2.52 | 0.11 |
| UTL | 0.027 | 6.99 | 0.20 | 0.104 | −1.14 | −0.10 |
| CON | 0.055 | 10.51 | 0.58 | 0.206 | 0.36 | 0.08 |
| SAL | 0.078 | 12.11 | 0.89 | 0.140 | 1.79 | 0.19 |
| HOT | 0.019 | 11.66 | 0.21 | 0.053 | −0.05 | 0.00 |
| T&S | 0.052 | 8.05 | 0.42 | 0.102 | −1.12 | −0.11 |
| P&T | 0.013 | 14.93 | 0.18 | 0.023 | 1.80 | 0.05 |
| FIN | 0.041 | 11.04 | 0.38 | 0.061 | 1.92 | 0.02 |
| REA | 0.039 | 9.05 | 0.33 | 0.054 | −8.10 | −0.46 |
| BUS | 0.023 | 10.67 | 0.26 | 0.054 | 0.68 | −0.02 |
| ADM | 0.032 | 10.78 | 0.36 | 0.060 | −0.31 | −0.04 |
| EDU | 0.025 | 4.05 | 0.11 | 0.042 | −2.42 | −0.09 |
| HEA | 0.012 | 5.92 | 0.06 | 0.031 | −1.29 | −0.05 |
| SER | 0.017 | 8.05 | 0.16 | 0.035 | −2.29 | −0.04 |
| Sum | 1.000 | 8.94 | 2.610 | 0.52 | ||
|
Notes: See Table A1 for industry abbreviations; growth rates are annualised raw growth rates in per cent; industry contribution to growth is weighted growth rate in percentage points; see Equation (9) for Domar aggregation |
||||||
Footnotes
This is a preliminary update of my earlier paper (Wu forthcoming). I am indebted to helpful discussions from James Laurenceson, Yong Wang, Xuehui Han, John Simon, Yiping Huang, Wing Thye Woo, Yanrui Wu, Rod Tyers, Peter Robertson and Ligang Song as well as participants at conferences and seminars at the RBA, Australian National University, University of Western Australia, Hong Kong University of Science and Technology, Asian Development Bank Institute, International Development Enterprises and Asia KLEMS. The results reported in this paper are interim results of the China Industrial Productivity (CIP) Database project supported by RIETI's East Asian Industrial Productivity Project and IER at Hitotsubashi University. The author is solely responsible for any errors. [*]
KLEMS is used as an acronym for K(C)apital, Labor, Energy, Materials and Services that are used to produce any product. By the same token, the gross output of an industry equals the total costs of ‘KLEMS’ and the gross output of an economy equals the sum of the costs of KLEMS of all industries. See O'Mahony and Timmer (2009) for an introduction to the EU KLEMS database. The ongoing CIP Database project is integrated with the World KLEMS initiative based at Harvard University. [1]
This is conditional on whether they can repeatedly negotiate for benefits regardless of their true performance. Here we assume that this is not the case. [2]
Strictly speaking, as suggested by Marcel Timmer, the effect of government interventions or regulations on individual industries should be examined by some policy proxies and its impact should be investigated through input-output table analysis. [3]
The CIP project is based on my China growth and productivity database project, self-initiated in 1995 and heavily involved in Angus Maddison's work on China's aggregate economic performance from 1912 and manufacturing, mining and utility industries from 1949 (see Maddison (1998, 2007); Maddison and Wu (2008)). The CIP project began in 2010, aiming to extend my earlier work to all non-industrial sectors under the KLEMS framework. [4]
China's official estimates of GDP growth have long been challenged for upward bias (see Wu (2013, 2014) for reviews). Alternative estimates have indeed shown slower growth rates than the official estimates, which inevitably also have level effects. The most affected sectors identified are manufacturing and so-called ‘non-material services’ (including non-market services). Wu (2013) shows that the official industrial output index has substantially moderated the impact of all external shocks. Wu (2014) also shows that the 5–6 per cent annual growth of labour productivity in non-material services based on official data appears to be too fast to be true if considering the international norm in history of between −1 and +1 per cent per annum (Griliches 1992; van Ark 1996). [5]
See Wu and Ito (2015) for very preliminary growth estimates at industry level using the double-deflation approach, although our work on prices is ongoing. [6]
China's retail price index (RPI) declined from 380.8 in 1997 (1978 = 100) to 346.7 in 2003, and meanwhile the PPI declined from 315.0 to 299.3 (NBS 2014, p 123). [7]
We are not yet able to include rent-weighted land growth as an input, which would be negative as more and more land is taken out of agricultural production. This may exaggerate the weight on labour, but it is difficult to say the likely direction of the bias in the estimated TFP. [8]
Here I would like to acknowledge Mun S Ho's important comment that the negative TFP may also indicate some data problem caused by conceptual issues, such as how to properly measure the depreciation of pipelines and exploration costs, which may result in poor capital measurement. [9]
Table A2 reports the details for individual industries. [10]
This might be due to the limited set of asset types (‘structures’ and ‘equipment’) that is available in the current CIP database. If a distinction between information and communications technology (ICT) and non-ICT assets could be made, a higher measured contribution is to be expected. [11]
I am indebted to Marcel Timmer for the discussion of the role of Chinese agriculture in the productivity performance of the aggregate economy. [12]
References
Bosworth B and SM Collins (2008), ‘Accounting for Growth: Comparing China and India’, Journal of Economic Perspectives, 22(1), pp 45–66.
Cao J, MS Ho, DW Jorgenson, R Ren, L Sun and X Yue (2009), ‘Industrial and Aggregate Measures of Productivity Growth in China, 1982–2000’, The Review of Income and Wealth, 55(Supplement s1), pp 485–513.
CPCCC (Communist Party of China Central Committee) (2013), ‘中共中央关于全面深化改革若干重大问题的决定’ (CCP Central Committee Resolution Concerning Some Major Issues in Comprehensively Deepening Reform), Passed at the 3rd Plenum of the 18th Central Committee of the Chinese Communist Party on 12 November 2013.
Denison EF (1962), The Sources of Economic Growth in the United States and the Alternative before Us, Supplementary Paper No 13, Committee for Economic Development, New York.
Domar ED (1961), ‘On the Measurement of Technological Change’, The Economic Journal, 71(284), pp 709–729.
Griliches Z (1960), ‘Measuring Inputs in Agriculture: A Critical Survey’, Journal of Farm Economics, 40(5), pp 1411–1427.
Griliches Z (1992), ‘Introduction’, in Z Griliches (ed), Output Measurement in the Service Sectors, NBER Studies in Income and Wealth, Vol 56, University of Chicago Press, Chicago, pp 1–22.
Huang Y (2012), ‘How Did China Take Off?’, Journal of Economic Perspectives, 26(4), pp 147–170.
Huang Y and K Tao (2010), ‘Factor Market Distortion and the Current Account Surplus in China’, Asian Economic Papers, 9(3), pp 1–36.
Hulten CR (1978), ‘Growth Accounting with Intermediate Inputs’, The Review of Economic Studies, 45(3), pp 511–518.
Hulten CR and FC Wykoff (1981), ‘The Measurement of Economic Depreciation’, in CR Hulten (ed), Depreciation, Inflation, and the Taxation of Income from Capital, The Urban Institute Press, Washington DC, pp 81–125.
Jorgenson DW (1966), ‘The Embodiment Hypothesis’, Journal of Political Economy, 74(1), pp 1–17.
Jorgenson DW, FM Gollop and BM Fraumeni (1987), Productivity and U.S. Economic Growth, Harvard Economic Studies Vol 159, Harvard University Press, Cambridge.
Jorgenson DW and Z Griliches (1967), ‘The Explanation of Productivity Change’, The Review of Economic Studies, 34(3), pp 249–283.
Jorgenson DW, MS Ho and KJ Stiroh (2005a), ‘Growth of U.S. Industries and Investments in Information Technology and Higher Education’, in C Corrado, J Haltiwanger and D Sichel (eds), Measuring Capital in the New Economy, NBER Studies in Income and Wealth Vol 65, University of Chicago Press, Chicago, pp 403–472.
Jorgenson DW, MS Ho and KJ Stiroh (2005b), Productivity, Volume 3: Information Technology and the American Growth Resurgence, MIT Press, Cambridge.
Jorgenson DW and KJ Stiroh (2000), ‘Raising the Speed Limit: U.S. Economic Growth in the Information Age’, Brookings Papers on Economic Activity, 2000(1), pp 125–210.
Li H and L-A Zhou (2005), ‘Political Turnover and Economic Performance: The Incentive Role of Personnel Control in China’, Journal of Public Economics, 89(9–10), pp 1743–1762.
Maddison A (1998), Chinese Economic Performance in the Long Run, Development Centre Studies, OECD Publishing, Paris.
Maddison A (2007), Chinese Economic Performance in the Long Run: Second Edition, Revised and Updated 960-2030 AD, Development Centre Studies, OECD Publishing, Paris.
Maddison A and HX Wu (2008), ‘Measuring China's Economic Performance’, World Economics, 9(2), pp 13–44.
NBS (National Bureau of Statistics of China) (comp) (2014), China Statistical Yearbook 2014, China Statistics Press, Beijing.
O'Mahony M and MP Timmer (2009), ‘Output, Input and Productivity Measures at the Industry Level: The EU KLEMS Database’, The Economic Journal, 119(538), pp F374–F403.
Perkins DH and TG Rawski (2008), ‘Forecasting China's Economic Growth to 2025’, in L Brandt and TG Rawski (eds), China's Great Economic Transformation, Cambridge University Press, Cambridge, pp 829–886.
Timmer MP, T van Moergastel, E Stuivenwold, G Ypma, M O'Mahony and M Kangasniemi (2007), ‘EU KLEMS Growth and Productivity Accounts Version 1.0: PART I Methodology’, Methodology of the March 2007 Release.
van Ark B (1996), ‘Sectoral Growth Accounting and Structural Change in Post-War Europe’, in B van Ark and N Crafts (eds), Quantitative Aspects of Post-War European Economic Growth, Cambridge University Press, Cambridge, pp 84–164.
Wu HX (2008), ‘Measuring Capital Input in Chinese Industry and Implications for China's Industrial Growth Performance, 1949–2005’, Presentation at the 2008 World Congress on National Accounts and Economic Performance Measures for Nations, Arlington, 12–17 May.
Wu HX (2013), ‘How Fast Has Chinese Industry Grown? – The Upward Bias Hypothesis Revisited’, China Economic Journal, 6(2-3), pp 80–102.
Wu HX (2014), ‘The Growth of “Non-Material Services” in China: Maddison's “Zero-Labor-Productivity-Growth” Hypothesis Revisited’, Institute of Economic Research The Economic Review, 65(3), pp 265–283.
Wu HX (2015), ‘Constructing China's Net Capital and Measuring Capital Services in China, 1980–2010’, The Research Institute of Economy, Trade and Industry RIETI Discussion Paper Series 15-E-006.
Wu HX (forthcoming), ‘On China's Strategic Move for a New Stage of Development – A Productivity Perspective’, in DW Jorgenson, K Fukao and MP Timmer (eds), The World Economy: Growth or Stagnation?, Cambridge University Press, Cambridge.
Wu HX and K Ito (2015), ‘Reconstructing China's Supply-Use and Input-Output Tables in Time Series’, The Research Institute of Economy, Trade and Industry RIETI Discussion Paper Series 15-E-004.
Wu HX and EYP Shea (2008), ‘China’, in JM Fanelli (ed), Macroeconomic Volatility, Institutions and Financial Architecture: The Developing World Experience, Palgrave Macmillan, New York, pp 125–156.
Wu HX and X Xu (2002), ‘Measuring the Capital Stock in Chinese Industry – Conceptual Issues and Preliminary Results’, Presented at the International Association for Research in Income and Wealth 27th General Conference, Djurhamn, 18–24 August.
Wu HX and X Yue (2003), ‘Sources of Quality Change in the Labour Input of Chinese Industry, 1955–2000’, Presented at the Western Economic Association International 5th Biennial Pacific Rim Conference, Taiwan, 9–12 January.
Wu HX and X Yue (2010), ‘Accounting for Labor Input in Chinese Industry, 1949–2005’, Paper presented at the International Association for Research in Income and Wealth 31st General Conference, St-Gallen, 22–28 August.
Wu HX and X Yue (2012), ‘Accounting for Labor Input in Chinese Industry, 1949–2009’, The Research Institute of Economy, Trade and Industry RIETI Discussion Paper Series 12-E-065.
Wu HX, X Yue and GG Zhang (2015), ‘Constructing Annual Employment and Compensation Matrices and Measuring Labor Input in China’, The Research Institute of Economy, Trade and Industry RIETI Discussion Paper Series 15-E-005.
Wu J (2008), 中国增长模式抉择 (The Choice of China's Growth Model), 3rd edn (rev), Shanghai Far East Press, Shanghai.
Xu C (2011), ‘The Fundamental Institutions of China's Reforms and Development’, Journal of Economic Literature, 49(4), pp 1076–1151.