Bulletin – March 2012 Extracting Information from Financial Market Instruments

Introduction

Financial market data are often used to extract information of interest to policymakers, such as market expectations for economic variables. The prices of interest rate securities are particularly useful for obtaining information about expectations of future risk-free interest rates and future inflation rates, as well as for estimating risk-free zero-coupon yield curves.

The first part of this article discusses how data from the overnight indexed swap (OIS) market and the government bond market can be used to estimate risk-free zero-coupon yield curves and obtain information about market expectations of the path of risk-free rates. OIS contracts directly reference the cash rate, making it relatively easy to extract market expectations from them, but they are only liquid out to around one year in maturity. To obtain estimates of zero-coupon risk-free interest rates beyond one year, models can be used to estimate a zero-coupon yield or forward curve from the yields on Commonwealth Government securities (CGS). The yield curve gives the interest rate agreed today for borrowing until a date in the future, while the forward curve gives the interest rate agreed today for overnight borrowing at a date in the future. The forward curve can be used as an indicator of the path of expected future cash rates, but importantly it becomes less reliable as the tenor lengthens because of the existence of various risk premia, for example term premia. No attempt is made in this article to adjust for these risk premia and so they will affect the estimated zero-coupon curves.^[1]

The second part of this article discusses how data from inflation swaps and the inflation-indexed Treasury capital indexed bond (CIB) market can be used to obtain estimates of inflation expectations. Conceptually, inflation swaps can be used in a similar way to OIS contracts, and CIBs can be used in a similar way to CGS, to extract information on expected inflation. In practice, inflation swaps tend to be the more useful source of information as there are very few inflation-indexed bonds on issue and the CIB market is somewhat less liquid than CGS. Inflation swaps are also traded at a larger number of tenors and have maturities extending from 1 to 30 years. Again risk premia, including liquidity and term premia, are present in the CIB and inflation swap markets, and so will affect the estimates.

Extracting Information on Cash Rate Expectations

Overnight indexed swaps are frequently traded derivative instruments where one party pays another a fixed interest rate on some notional amount in exchange for receiving the average cash rate on the notional amount over the term of the swap. The cash rate is the rate on unsecured loans in the overnight interbank market, which is the Reserve Bank's (RBA) operational target for monetary policy. Banks and other market participants use trades in OIS to manage their exposure to interest rate risk. For example, a market participant expecting a reduction in the cash rate may choose to trade on this expectation by entering an OIS contract where they receive a fixed rate and pay the actual cash rate over the period of the swap; a party with a lower expectation of a reduction in the cash rate may enter the opposite transaction. OIS rates therefore provide direct information on market expectations of monetary policy.

The OIS market has grown considerably since its inception in 1999. As at June 2011 there were $3.2 trillion of OIS contracts outstanding, and turnover in the year to June 2011 was around $6.6 trillion (Graph 1). Since OIS rates reflect the return from investing cash overnight over the term of the swap, and there is only an exchange of interest – not notional principal amounts – these transactions involve very little term or counterparty credit risk. An important point, however, is that these risks in OIS are not zero, as is often assumed, and are likely to increase, along with the associated risk premia, in times of stress.^[2] Generally though, OIS rates tend to be lower and less volatile than other money market rates of similar maturity. For example, bank bill futures contracts, which reference the 90-day bank bill swap (BBSW) reference rate, are liquid but are less useful for extracting unbiased cash rate expectations because they incorporate a greater degree of credit risk which can change, and has changed, over time.

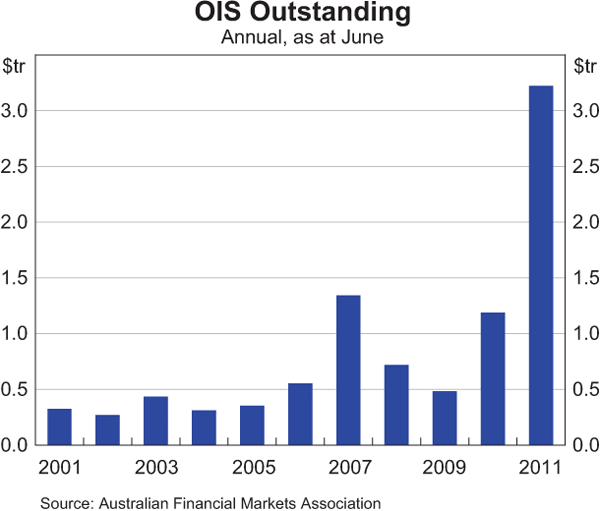
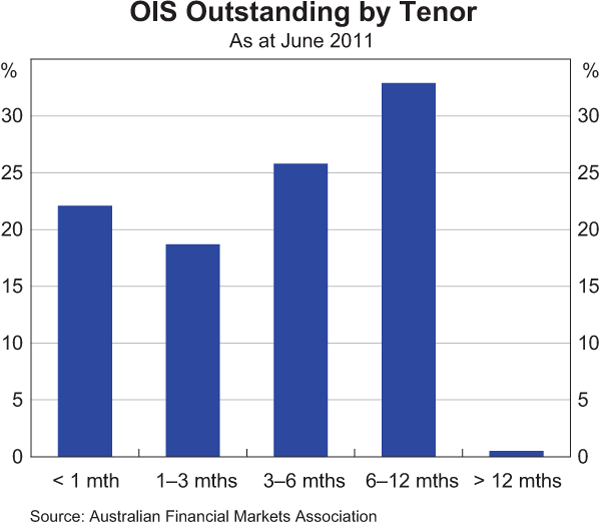
OIS contracts trade for relatively short terms, generally of less than one year. Of the total amount of OIS contracts outstanding in June 2011, around 40 per cent was for contracts with a term of less than 3 months, 26 per cent was for contracts with terms of between 3 and 6 months and 33 per cent was for terms of between 6 and 12 months (Graph 2).

OIS have advantages over the 30-day interbank cash rate futures contracts trading on the ASX. These contracts are similar in concept to OIS, but they are exchange-traded and have fixed maturity dates as opposed to fixed tenors. Also, less trading occurs in these contracts than in OIS, especially for contracts of over three months. The relatively high level of liquidity that usually exists in OIS markets means that they are typically quoted with small bid-offer spreads, which helps users to derive more accurate measures of market expectations of the cash rate. Another theoretical advantage of OIS is that, being a derivative instrument, the supply of OIS contracts is not fixed; supply factors can influence the pricing of physical securities, such as bank bills and certificates of deposit.

The use of the OIS market to gauge cash rate expectations does, however, present some challenges. OIS rates can sometimes be distorted by a lack of liquidity as well as positioning from market participants, for example those wishing to trade on the basis of views about the likelihood of large and unexpected ‘tail events’ adversely affecting economic conditions. They also incorporate some term and counterparty credit risk as discussed earlier. These distorting factors are more likely to be relevant during times of heightened uncertainty about the economic and financial outlook, as has been the case recently.

OIS rates nonetheless provide a useful and simple source of data for estimating cash rate expectations out to one year. If, for example, the fixed rate in an OIS is trading below the current cash rate, this would indicate that, on average, market participants are expecting the RBA to ease monetary policy over the term of the swap. By comparing the fixed rates for swaps of different maturities, it is possible to assess both the magnitude of the expected change in the cash rate and the timing of these changes. As a simplified example, assume that the day before an RBA Board meeting:

• the current cash rate is 4.25 per cent;
• the 30-day OIS rate (i.e. the fixed rate) is 4.00 per cent; and
• the 60-day OIS rate is 3.875 per cent.

The 30-day OIS rate of 4.00 per cent suggests that market participants are, on balance, expecting the cash rate over the next 30 days to average that rate. If for the sake of simplicity it is assumed that the Board will only move the cash rate in 25 basis point increments – whereas the market can often expect larger adjustments – then it follows that financial market participants expect the RBA to cut the cash rate by 25 basis points at the next day's Board meeting.^[3] Comparing the 30-day and 60-day OIS rates also indicates what markets are expecting to happen to the cash rate at the subsequent RBA meeting. If the market is expecting that the cash rate will average 4.00 per cent for the next 30 days and 3.875 per cent for the next 60 days, then the market must be expecting the cash rate during the second 30-day period to average 3.75 per cent (that is, (4.00 + 3.75) / 2 = 3.875).

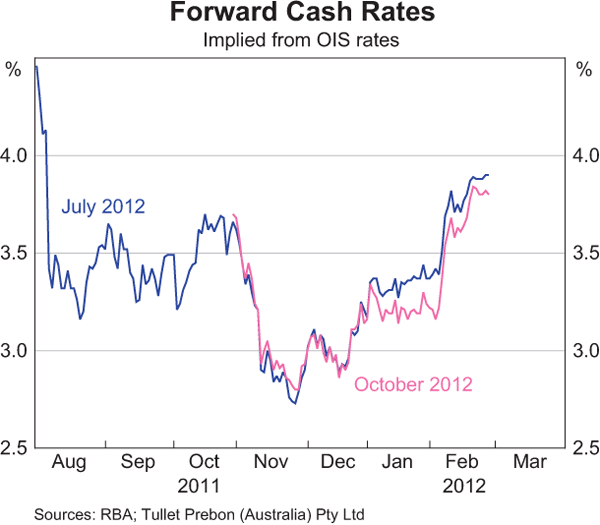
Market expectations of the cash rate can vary substantially over time. At the time of writing this article, expectations of the cash rate for the middle of 2012 were around 4 per cent, up from around 3 per cent late last year when concerns stemming from the European sovereign debt crisis weighed heavily on sentiment about the economic outlook (Graph 3).

While OIS rates provide information about the short end of the yield curve, they are less useful for the longer end, as they cease to be regularly traded for maturities beyond around one year. At longer maturities, the natural risk-free interest rates to consider are those on CGS (other ‘risk-free’ bonds exist, such as government-guaranteed bank bonds, but such bonds typically trade with a significant liquidity premium relative to CGS so they are not considered here). There are currently 18 CGS lines on issue, with remaining terms to maturity ranging from less than 1 year to a little over 15 years.

There are a number of factors to consider when using CGS yields to calculate longer-term risk-free interest rates. First, investors in a 10-year bond with coupons receive a cash payment not only in 10 years time, when the bond matures, but every 6 months leading up to maturity. This in turn means that the interest rate associated with the bond – the yield to maturity – is not the risk-free interest rate for borrowing for 10 years, but rather a combination of the 10-year interest rate, which applies to the principal payment, as well as the various interest rates applying to the coupons paid over the life of the bond. Second, the limited number of CGS on issue also means that one can only look at interest rates to certain dates in the future. Estimating zero-coupon yield and forward curves resolves these problems: the impact of coupons on bond prices is explicitly modelled and removed, and the estimated curves allow the gaps in between bond maturities to be ‘filled in’.

Details of the estimation method are provided in Appendix A. For data, prior to 2001 Treasury notes for maturities extending up to one year into the future are used, and from 2001 onwards OIS rates for maturities extending up to one year are used (the OIS market became liquid enough to provide reliable pricing around this time, while Treasury notes were not issued between mid 2002 and early 2009). CGS yields are used for maturities greater than 18 months into the future (bonds with short maturities can be relatively illiquid in comparison with longer-dated CGS).

As such, the yield curves that are estimated combine data from both the OIS and CGS markets, with the implicit assumption that the interest rates attached to all instruments in both markets are largely free of credit and liquidity risk premia, and therefore comparable. To the extent that this does not hold, it will flow through to the estimated curves. The existence of term premia, being the extra compensation demanded for investing for a longer period of time, is another complicating factor. Again no attempt is made to account for term premia and so any term premia in OIS rates or bond prices will be incorporated in the estimated curves.

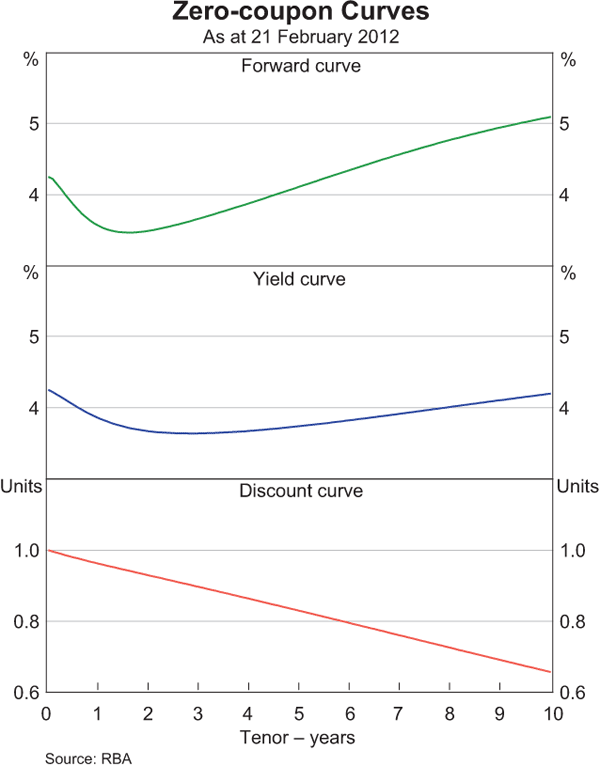
Notwithstanding these caveats, estimated zero-coupon forward, yield and discount curves as at 21 February 2012 are given in Graph 4. The discount curve gives the value today of receiving one dollar in the future; it starts at one (one dollar today is worth one dollar) and slopes down (one dollar today is worth more than one dollar in the future). Although the discount curve looks linear at this scale, it is not. The forward and yield curves start at the prevailing cash rate. As discussed earlier, abstracting from the existence of risk premia, the forward rate can be read as giving a rough indication of the market-implied expectation for the cash rate. On this basis, as at 21 February 2012, OIS rates and CGS prices implied that market participants expected the cash rate to fall over the year ahead before rising again over subsequent years. The yield curve is essentially an average of the forward curve and so looks broadly similar to, but is generally smoother than, the forward curve.

Graph 5 provides a longer perspective on the data, showing zero-coupon forwards since 1993 at the 1-, 3- and 5-year horizons. These discount, yield and forward curves are available to the public on the RBA website.

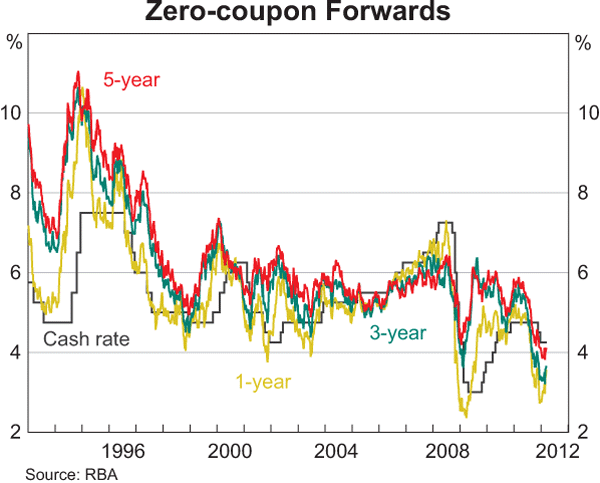
Zero-coupon discount, yield and forward curves can be used in a number of applications. A common way to use this kind of data is as an input for discounting future cash flows, be they cash flows from real assets such as toll roads or power stations, or cash flows from financial assets such as shares or bonds. This discounting essentially assigns a current dollar value to future payments or receipts and is most easily achieved using a discount curve, although to discount risky cash flows a discount curve that incorporates an appropriate risk premium should be used.

Zero-coupon yield curves are also useful for analysing the government bond market itself; for example, the deviation of traded bond prices from prices implied by the fitted zero-coupon yield curve (that is, the pricing error made in fitting the model) may indicate that certain bonds are cheap or dear relative to other bonds with similar maturities.

Another use is in economic modelling. Economists are interested in the interaction of financial markets and the real economy, including the effect that interest rates have on the real economy. To study these relationships zero-coupon yields should be used, not yields to maturity (see, for example, Spencer and Liu (2010) for a recent study of economic and financial linkages).

There is also a large amount of literature on the estimation of the term premia present in government bonds. This literature attempts to decompose zero-coupon yields into pure cash rate expectations and a term premia component, and thereby derive better estimates of expectations (this article does not attempt to adjust for term premia). Term premia are also of interest in their own right, as they give an indication of the excess return an investor can expect from investing for a longer time period. Term premia estimation requires zero-coupon yields as the basic input into estimation (see, for example, Duffee (2002) for a US study on term premia, or Finlay and Chambers (2008) for an Australian study).

Extracting Information on Inflation Expectations

Reliable and accurate estimates of inflation expectations are important to central banks given the role of these expectations in influencing future inflation and economic activity. These expectations are also important for organisations that manage inflation-linked assets or liabilities. Although surveys provide some guidance on the expected path of inflation, inflation-linked securities have the advantage of providing more timely and frequently updated information on market expectations of inflation.

A widely used market-based measure of inflation expectations is a break-even inflation (BEI) rate calculated as the difference between the yields of nominal CGS and CIBs.^[4] The current BEI rate at the 10-year horizon is around 2¾ per cent, suggesting that the market expects average inflation over the next 10 years to be within the RBA's 2–3 per cent inflation target (Graph 6). For shorter maturities, markets currently expect inflation to be closer to 2½ per cent.

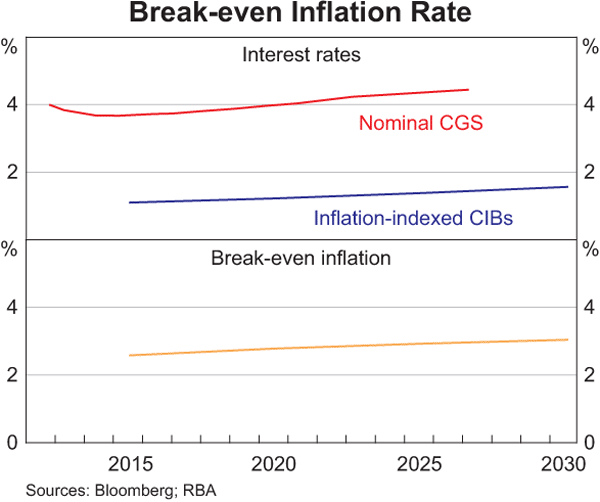
One limitation with using the bond market to gauge inflation expectations is the small number of CIBs on issue; there are only five bonds currently on issue, with maturities around every five years from 2015 to 2030. In comparison, there are 18 CGS lines on issue with maturities spanning 2012 to 2027. Hence, the bond market offers a limited number of pricing points from which to extract measures of inflation expectations for a broad range of tenors. This lack of pricing points also makes it more difficult to derive forward measures of expected inflation, which measure expectations of inflation at some point in the future.^[5]

In addition, there are maturity mismatches between CGS and CIBs. For example, the current 10-year CGS matures in July 2022 whereas the closest CIB matures in February 2022. As a result, a 10-year BEI rate must be derived by interpolation. Further adjustments must also be made to account for compounding effects on yields since CGS pay semi-annual coupons while CIBs pay quarterly coupons.

However, the most serious shortcoming of the BEI rate derived from bonds is that it captures investors' liquidity preferences for different types of bonds. With outstanding CIB issuance 13 times smaller than CGS, CIBs can be less liquid than CGS, and investors who wish to hold highly liquid assets will have a stronger preference for CGS. This liquidity preference effect can be very pronounced during periods of heightened uncertainty such as in 2008 where ‘flight-to-safety’ bids put significant downward pressure on nominal bond yields (as noted earlier, any such distortion will also be incorporated in the estimated nominal zero-coupon curves) (Graph 7). More broadly, with CGS yields trading with a liquidity premium relative to CIBs, BEI rates can be artificially compressed and so give a distorted measure of inflation expectations. The low BEI rates in 2008 and 2009 were not all driven by liquidity effects, however, since the financial crisis had led market participants to become more pessimistic about future economic conditions.

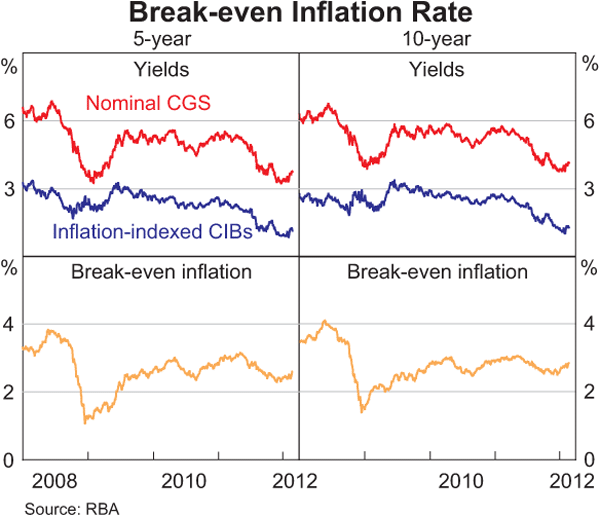
Because of these limitations, inflation swaps have become an increasingly popular alternative source of information on inflation expectations. Their key advantage is that they provide direct and readily available measures of inflation expectations with no need for interpolation, since swaps are traded at the main tenors of interest such as 3-, 5- and 10-years. Also, as derivatives, the supply of inflation swaps is not constrained, meaning that in theory, inflation swap rates are generally not distorted by liquidity preference effects.

An inflation swap is a transaction whereby the inflation payer pays the actual inflation rate in exchange for receiving a fixed payment (Figure 1). The actual inflation payment is based on the most recently available quarterly consumer price index at the maturity of the swap. The fixed payment approximates the expected value of inflation over the term of the swap and is analogous to the BEI rate derived from bond prices. In this sense, inflation swaps operate in a similar fashion to OIS contracts, but with a different reference rate (CPI inflation instead of the overnight cash rate) and longer terms to maturity. Fixed rates for inflation swaps are readily available for terms out to 30 years.

The most common form of inflation swap in the market is the zero-coupon inflation swap. Here only one cash payment is made at the maturity of the swap, representing the difference between the fixed rate and actual inflation over the term of the swap. This means that counterparty credit risk is minimal and inflation swap rates are not affected by periodic coupon payments. Zero-coupon inflation swaps have become more popular over recent years, especially between 2003 and 2009 when CIB issuance ceased.

In terms of hedging flows, the main receivers of inflation in the inflation swap market are pension funds that use swaps to match their long-term inflation-linked liabilities. Liability matching has had a significant impact on making the inflation swap market in Australia a more recognised alternative to inflation-indexed bonds. Demand to pay inflation in swaps (and receive a fixed rate) mainly stems from infrastructure project providers that want to hedge their inflation-linked assets or revenue streams. This can be done by issuing a nominal bond and entering into an inflation swap with an investment bank. This has boosted the size of the inflation swap market, which is an over-the-counter market where intermediaries such as prime brokers play an important market-making role.

Investors can also trade inflation swaps based on their views about future inflation. For example, if an investor expects a higher rate of inflation than that implied by the fixed rate of a swap, the investor would enter a swap contract, receive actual inflation and pay the fixed rate. This is achieved through a single transaction instead of separate trades in nominal and inflation-indexed bonds, which bear funding costs and suffer from maturity mismatches. Inflation swaps are also used in conjunction with nominal bonds to replicate an inflation-indexed bond. This allows investors to overcome bond maturity mismatches as well as any potential shortage of inflation-indexed bonds.

Despite the recent growth in inflation swaps, the market remains small compared with those for other derivatives such as interest rate swaps. There are no official data to measure the total size and activity levels in the inflation swap market accurately, although a survey by the Australian Financial Markets Association (AFMA) estimated that as at May 2011 there were $24 billion of inflation swaps outstanding, and turnover over the year to June 2011 was $11.6 billion (AFMA 2011).

Since 2008, measures of implied inflation captured by 3-, 5- and 10-year inflation swaps have ranged between 1¼ per cent and 4 per cent (Graph 8). Mimicking the pattern observed for the BEI rate from the bond market, inflation swap rates over 2008 also fell to low levels, suggesting that market participants were moderating their inflation expectations. Over recent years, however, these inflation expectations have reverted to around 2–3 per cent.

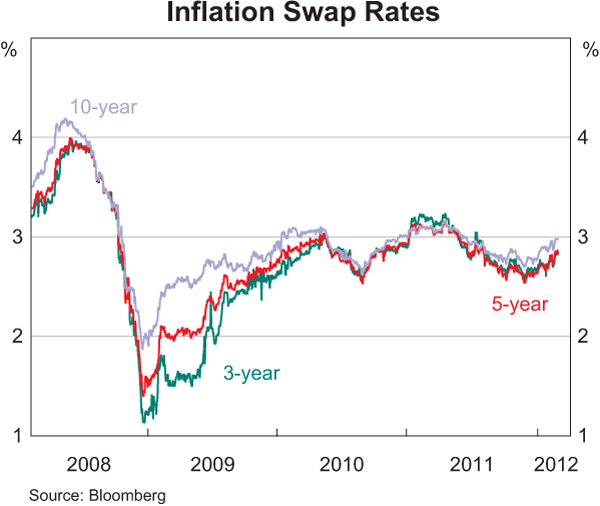
Since inflation swap rates are zero-coupon, it is simple to use the framework in the previous section to derive forward inflation rates, which measure expectations of inflation at some point in the future (Graph 9). Forward inflation rates derived from swaps at the 3-, 5- and 10-year horizons have also fluctuated in a wide range over recent years; as these forward rates represent expected inflation at a point in the future, they are generally more volatile than the (zero-coupon yield) measures shown in Graph 8, which represent expected inflation over a period up until a point in the future. Overall, current forward measures of inflation are also around 2 to 3 per cent, albeit slightly above 3 per cent at the 10-year horizon.

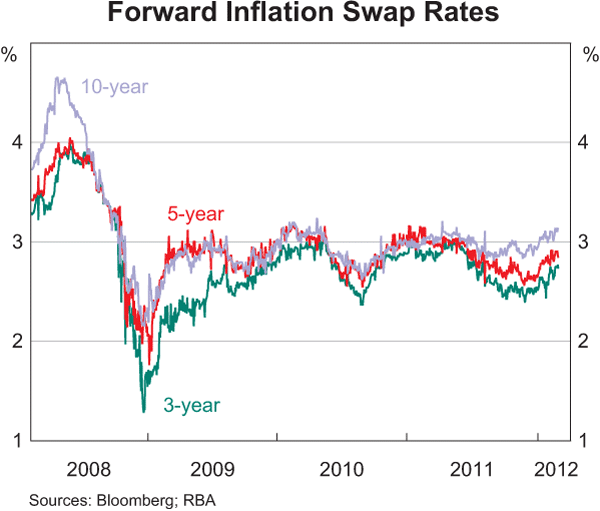
Inflation expectations in the swap market broadly track the BEI rate in the bond market, but current 5- and 10-year measures appear to show that inflation expectations in the swap market are somewhat higher than those in the bond market; over the first half of 2009 the divergence of the swap market from the bond market was even greater, with inflation swap rates being up to 50–70 basis points higher than BEI rates implied by bonds (Graph 10). One reason for this lower BEI rate from the bond market is the liquidity preference effect discussed earlier. This effect was particularly pronounced over the first quarter of 2009 when inflation swap rates normalised faster in the aftermath of the financial crisis than bond yields, which retained a large liquidity premium.

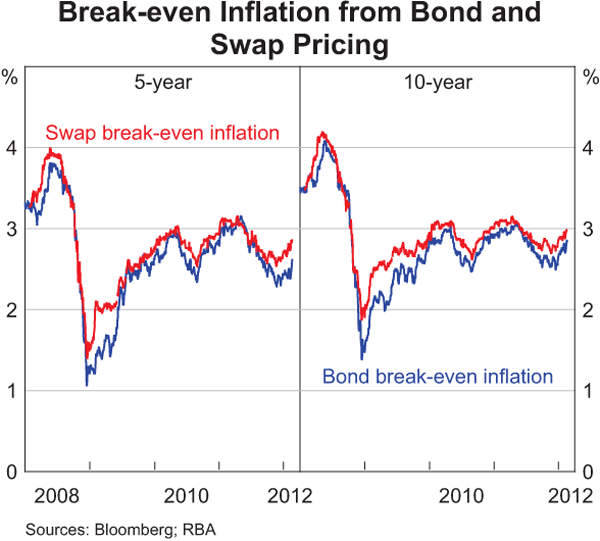
Another reason swap rates could be higher relates to hedging. Intermediaries in the swap market, who play an important market-making role, sometimes hedge their positions in the inflation-indexed bond market. This market can be relatively less liquid and compensation for this hedging risk may bias up inflation swap rates.

Term premia also tend to cause structurally higher inflation swap rates because the fixed-rate payer will demand compensation for the inherent uncertainty about the expected amount of inflation over the term of the swap. This premium can change for a variety of reasons including an increase in uncertainty about the inflation rate or changes in investors' inflation tolerance (term premia can also affect CIBs).

Conclusion

Financial markets provide a significant amount of information about expectations of the cash rate, risk-free rates and inflation. Extracting expectations from market measures is not always straightforward, however, and results should be viewed with some caution. Measures derived from the government bond market can contain liquidity preference effects that are particularly problematic in times of heightened uncertainty. Some measures, such as zero-coupon interest rates, are not directly observable and must be estimated from bond yields using a variety of assumptions. Nonetheless, as well as providing some information on risk-free rates, estimates of zero-coupon rates are useful in economic modelling, in estimating risk premia and for discounting cash flows. The RBA will be publishing a constructed series of zero-coupon yield, forward and discount curves on its website. While derivative instruments such as OIS and inflation swaps provide more straightforward measures of market expectations, and are regularly updated as these markets are actively traded, the prices of these instruments contain various risk premia, which tend to bias implied expectations.

Appendix A

There are a number of established methods for estimating zero-coupon curves, which all give broadly similar results (see, for example, Bolder and Gusba (2002)). The method used in this article – the Merrill Lynch Exponential Spline model – does not estimate the yield or forward curve directly, but instead estimates the discount curve, from which the zero-coupon yield and forward curves can be recovered.^[6] The discount curve is modelled as a linear combination of a number of underlying curves, called basis functions, which are fixed functions of time. That is, it is assumed that the discount curve can be written as:

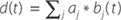
where b_j(t) are basis functions, and a_j are the (to be estimated) coefficients that, when multiplied with the basis functions, give the discount curve. The price of a bond, which can be observed, is simply each cash flow (consisting of coupon payments and principal) multiplied by the appropriate discount curve value. For example, if the cash flows of a bond are denoted by c_t then the bond price, P, can be written as:

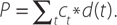
Taking the two equations above together, the cash flows c_t are known, and the basis functions b_j(t) are fixed functions of time, so the only unknowns are the coefficients attached to the basis functions, a_j. The same discount curve is used to price all bonds in the market, which allows the coefficients to be estimated. The model allows this estimation to be done within a standard regression framework, which is simple and fast (see Appendix A of Finlay and Chambers (2008) for further details).

Footnotes

Richard Finlay is from Economic Analysis Department and David Olivan is from Domestic Markets Department.
[*]

The zero-coupon yield, forward and discount curves presented in this article are available at <http://www.rba.gov.au/statistics/>. [1]

To earn the OIS rate over the term of the swap, the investor that receives the fixed rate of the swap will invest an amount equal to the swap's principal in the overnight interbank market. In doing so, the investor is exposed to the overnight credit risk of a bank counterparty, which can vary significantly in times of acute market stress. [2]

If this assumption is not made then the data would also be consistent with many different possibilities, such as a 50 per cent chance of a 50 basis point cut, a 25 per cent chance of a 100 basis point cut, etc. [3]

CIBs pay quarterly coupons that are fixed in real terms; both the dollar value of coupons and principal payable at maturity increase in line with movements in the consumer price index. [4]

Zero-coupon forward curves can be estimated for CIBs in a similar manner to that described in the previous section. With only five bonds on issue, however, such curves are not likely to provide an accurate description of market expectations. [5]

The yield curve, z(t), which gives the interest rate agreed today for borrowing from today until a time t in the future, is related to the discount curve, d(t), by z(t) = −log(d(t))/t, while the forward curve, f(t), is related to the yield curve by f(t) = z(t) + tz' (t). [6]

References

AFMA (Australian Financial Markets Association (2011), ‘2011 Australian Financial Markets Report’. Available at <http://www.afma.com.au/data/afmr.html>.

Bolder D and S Gusba (2002), ‘Exponentials, Polynomials, and Fourier Series: More Yield Curve Modelling at the Bank of Canada’, Bank of Canada Working Paper No 2002-29.

Duffee GR (2002), ‘Term Premia and Interest Rate Forecasts in Affine Models’, Journal of Finance, 57(1), pp 405–443.

Finlay R and M Chambers (2008), ‘A Term Structure Decomposition of the Australian Yield Curve’, RBA Research Discussion Paper No 2008-09.

Spencer P and Z Liu (2010), ‘An Open-economy Macro-finance Model of International Interdependence: The OECD, US and the UK’, Journal of Banking & Finance, 34(3), pp 667–680.