Research Discussion Paper – RDP 2020-01 Credit Spreads, Monetary Policy and the Price Puzzle
1. Introduction
A higher cash rate dampens economic activity and reduces inflation. This is the standard prediction of conventional macroeconomic theory and guides policy decisions of all inflation-targeting central banks. Yet identifying and quantifying this relationship using standard empirical methods proves to be a challenge. Instead, researchers frequently find the opposite: increases in the policy rate – in Australia, the cash rate – are followed by higher inflation.[1] This ‘price puzzle’ is commonly believed to result from the inability of researchers' models to fully capture the central bank's anticipatory response to future inflation (Sims 1992; Hanson 2004; Romer and Romer 2004). As the central bank raises the policy rate when it expects inflation to rise in the future, the policy rate and inflation will be positively correlated unless the empirical model fully captures the central bank's inflation outlook. According to this explanation, causality runs in reverse – higher future inflation causes the central bank to raise its policy rate.
To resolve this issue, Romer and Romer ((2004), hereafter RR) propose removing the anticipatory component of monetary policy by purging policy rate changes of the central bank's systematic response to its own inflation forecasts. Controlling directly for the central bank's outlook in this way successfully removes the price puzzle in US data. But following the same approach for Australia, Bishop and Tulip ((2017), hereafter BT) find the price puzzle to persist across a wide range of model specifications. If anything, estimates from a standard SVAR using cash rate changes purged of the Reserve Bank of Australia's (the Bank) forecasts show an even stronger price puzzle (Figure 1, right panel) than estimates that use the raw cash rate series (Figure 1, left panel). Similarly puzzling findings are obtained for the effects on the unemployment rate. An increase in the cash rate leads to lower unemployment initially.
Having accurate estimates of the effects of monetary policy is obviously crucial for an inflation-targeting central bank. Therefore, the robustness of these puzzles to a range of specifications shown in BT has cast doubt on the reliability of the RR approach (and time series methods more generally) to accurately quantify the causal effects of cash rate changes not only on inflation and the unemployment rate, but on other key variables of interest as well. So what explains the robust emergence of the price puzzle even when the Bank's inflation outlook is accounted for? And what are the effects of a cash rate change on key macroeconomic outcomes such as inflation?
1994:Q1–2018:Q4
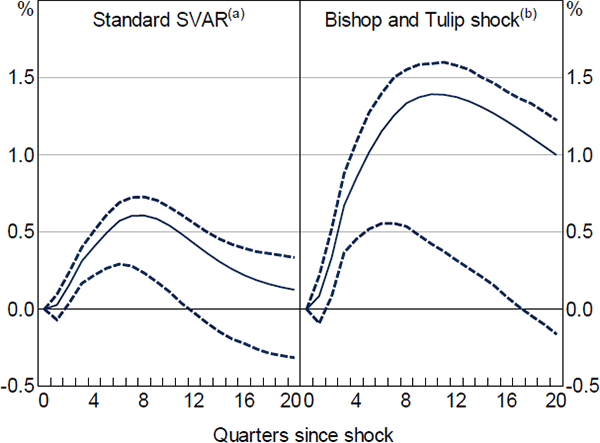
Notes:
Impulse responses from a recursive SVAR(4) including log underlying CPI, log real GDP, the unemployment rate and a monetary policy variable, in this order; dashed lines show 90% confidence intervals (bootstrapped)
(a) Policy variable is the cash rate
(b) Policy variable is the cumulated policy shock from Bishop and Tulip ((2017), updated)
In this paper I follow Caldara and Herbst (2019) and argue that the RR approach used by BT yields biased estimates of the true causal effects of monetary policy due to an omitted systematic and contemporaneous response of the cash rate to credit and money market conditions. Specifically, I show that the Reserve Bank Board responds immediately to expansionary financial market conditions (as indicated by low risk premia in lending and money market rates) by raising the cash rate over and above what the Bank's forecasts would demand. The cash rate response to these credit market conditions is sizeable. All else equal, a 100 basis point decline in money market risk spreads leads to a contemporaneous 60 basis point increase in the cash rate, and a 100 basis point decline in risk premia in large business lending rates is met by an 8 basis point cut to the cash rate.
But why does this additional response lead to the price puzzle when applying the RR approach to Australia? I document two further empirical relationships – each one on its own implying that the misspecification of the Bank's reaction function in BT violates two crucial conditions for the RR approach to provide unbiased estimates of the effects of monetary policy.
First, credit and money market risk spreads contain considerable additional predictive information for future inflation that is not captured by the Bank's forecast. In particular, I find inflation two to six quarters out to print systematically higher than forecast by the Bank when credit market conditions ease. While this supports the Board's decision to raise the cash rate to offset some of the inflationary impulse of easing financial conditions, it also violates the RR assumption that the Bank's forecasts contain all relevant information about the economic outlook on which the cash rate decision is based (RR; Ramey 2016). As a result, the RR ‘shock’ used by BT is, in fact, a mix between the true policy shock unrelated to the Bank's inflation outlook and the systematic, endogenous cash rate response to the inflationary effects of changing credit market conditions.[2] Accordingly, when estimates fail to take account of this systematic response, a future increase in inflation would be wrongly attributed to the higher cash rate rather than to expansionary financial market conditions.
Second, I show that cash rate changes – after accounting for the Bank's response to its own forecasts but not for the response to credit market conditions – are well anticipated by financial markets. This is unsurprising: if financial market participants were systematically surprised by the Board's response to publicly available financial market information, considerable profits could be earned by better predicting future cash rate changes. Accordingly, the RR shocks used by BT are anticipated and hence cannot be true structural policy shocks reflecting a primitive, unanticipated economic force that is unforecastable (and uncorrelated with other shocks) as in the definition of Ramey (2016) and Stock and Watson (2018). As a result, part of the effect of the BT shock would have affected some economic variables (e.g. the exchange rate) already before it is measured. This may be a further source of bias for the estimated policy effects in BT.[3] I demonstrate that a considerable part of this anticipatory component reflects the fact that market participants understand the Reserve Bank Board's systematic response to financial market conditions. As soon as the cash rate response to financial market conditions is taken into account, this predictable component shrinks considerably.
Taking these findings into account successfully resolves the price puzzle. To gauge the relevance of both potential sources of bias, I address them in turn. Specifically, I first construct a new series of monetary policy shocks that purges cash rate changes not only of the Bank's forecasts for inflation and economic activity but also of the response to several measures of risk premia in lending and money market rates. This shock still conceptually follows the RR approach and identifies shocks as a deviation of monetary policy from its historical reaction function. Using this series of shocks removes the price puzzle and leads to an earlier rise of the unemployment rate in response to a contractionary policy shock. However, I find that this policy shock measure is still partially anticipated by financial market participants.
To further remove this predictable component, I then also purge this shock series of the cash rate change expected by financial market participants ahead of the Board meeting. This two-step procedure follows Barakchian and Crowe (2013) and Miranda-Agrippino and Ricco (2018) and relates to the large literature that uses (high frequent) financial market information to identify policy surprises and uses these surprises as ‘shocks’ (e.g. Kuttner 2001; Cochrane and Piazzesi 2002; Gürkaynak, Sack and Swanson 2005; Gertler and Karadi 2015). While this information is ideal to ensure that the shock is unanticipated, in itself, it does not necessarily ensure that it is also exogenous to the Bank's outlook for the economy. However, this is not an issue for my final, preferred shock series which is purged of this component in the first step and thereby combines the benefits of both strands of the literature on identifying monetary policy shocks.
Using this new series of shocks I find that inflation, economic activity and the labour market respond in line with expectations. My results suggest that prices fall by around 0.7 per cent over the two years following a 100 basis point temporary increase in the cash rate, the unemployment rate peaks after six quarters at around one-third of a percentage point above its previous level and output falls by around 0.8 per cent over the course of one year. While subject to a considerable degree of uncertainty, the estimated response of inflation is about twice as large as the inflationary effects of a cash rate increase in MARTIN, the Bank's preferred macroeconometric model (Ballantyne et al 2019). In contrast, the estimated responses of output and the unemployment rate are closely in line with the dynamic responses in MARTIN. While this provides some comfort that MARTIN accurately captures the macroeconomic effects of a change to the Bank's key policy tool, it suggests that monetary policy may be more effective in raising or reducing inflation than suggested by MARTIN.[4]
Overall, my findings emphasise the importance for understanding the effect of credit market shocks not only to the wider economy, but also for the conduct and efficacy of monetary policy. As such, my results are closely related to the findings of Caldara and Herbst (2019) for the United States. Similarly to these authors, I find that omitting the systematic, contemporaneous response of monetary policy to exogenous changes in credit market conditions leads to biased estimates of the effect of policy on inflation. As the cash rate rises in response to a decline in credit risk premia, which in itself raises credit supply, economic activity and, ultimately, inflation, the bias is positive and the price puzzle emerges. For the RR identification strategy, however, this rests on my novel finding that changes in credit market conditions are an important source of the central bank's inflation forecast errors.
1.1 Why Does the Bank Adjust the Cash Rate but Not the Inflation Forecast?
The active cash rate response to credit market spreads in the apparent absence of an adjustment of the Bank's central forecasts to information in those spreads appears puzzling at first. I consider several explanations for this tension. First, the Reserve Bank Board (the Board) may rely on their own central forecasts when setting the cash rate. However, this appears unlikely since both forecasts and policy decisions are led by the Bank's Governor and Deputy Governor (Bishop and Tulip 2017). Second, when producing the forecasts, the Bank's staff may anticipate the Board's offsetting cash rate response. Again, this appears unlikely since changes to the cash rate are typically believed to take some time to affect inflation and I find credit spreads to explain the Bank's short- to medium-term forecast errors. Third, my proxies for credit market conditions may capture international (financial or monetary policy) conditions more broadly (Rey 2015). While international financial conditions are certainly important to Australia, I find that domestic money and credit market spreads explain the cash rate response even after accounting for the US policy rate or exchange rate movements.
Fourth, the predictive content of credit market indicators for the Bank's inflation forecast errors may reflect a lack of understanding on part of the Bank of the importance of smooth credit market functioning for the real economy prior to the global financial crisis (GFC) – a common criticism of central banks and the macroeconomics profession in the aftermath of the GFC (Debelle 2018).[5] Perhaps in line with this, I find some evidence that the Bank has learned from the GFC experience and now better integrates financial market developments into its economic outlook. In particular, the predictive content of credit market indicators for the Bank's forecast errors breaks down (in the admittedly short sample) after the GFC. Furthermore, I find that the cash rate has responded more decisively to changes in business lending rate spreads since the GFC, thereby more strongly offsetting any macroeconomic effects. However, the hypothesis of a lack of understanding of the importance the credit market conditions does not explain why the Board has responded to financial market conditions over the entire sample when setting the cash rate.
Finally, and most plausibly in my view, credit spreads may provide important information to the Board about the risks around the Bank's central, model-based forecasts. Accordingly, the Board may follow a risk management approach in which it weighs both ‘hard’, quantitative information that enters the Bank's central forecasts with ‘soft’, qualitative advice on the risks around those forecasts when setting the cash rate. Evans et al (2015) and Caggiano, Castelnuovo and Nodari (2018) provide evidence for this for the US Federal Reserve (the Fed), showing that it sets a lower policy rate than what its internal forecasts would suggest when uncertainty is elevated. Similarly, Sharpe, Sinha and Hollrah (2017) find that ‘tonality’ of the narrative around the Fed's forecasts predicts not only the Fed's forecast errors for GDP and unemployment, but also explains the policy decision over and above the Fed's forecasts. As I outline in the next section, credit and money market spreads may serve as a similar instrument informing the Reserve Bank Board about risks around the staff's central forecasts. During the GFC, this motivated strong cuts to the cash rate. Theoretical support for such a risk management approach has since been provided by Adrian and Duarte (2016), who argue that such an approach may be optimal at times of financial stress.[6] Importantly, while risks from financial stress are regularly discussed in the supporting documents provided to the Board by the Bank staff and in the Board meetings, they are not observed by the researcher who follows the RR approach. This may explain why the RR approach fails to recover the true causal effects of a cash rate change.
The body of this paper presents the arguments for bias in the RR approach arising from an omitted response to credit market conditions in detail. I begin by formally showing under which conditions the RR approach suffers from the same omitted variable bias that it aims to solve. I also provide some narrative evidence around the GFC, during which financial market conditions and risks to the outlook strongly influenced the decisions to lower the cash rate whilst the Bank's central forecasts were adjusted only with a considerable delay. In Sections 3 and 4, I then show that this relationship between credit spreads, the cash rate and the Bank's forecast errors is systematic such that both necessary conditions for bias in the RR approach are fulfilled. The cash rate responds to money market and credit spreads over and above the Bank's forecasts (Section 3), and these spreads explain the Bank's forecast errors for inflation (Section 4). I build on these findings in Section 5 to construct a new measure of monetary policy shocks for Australia and show that an increase in the cash rate reduces inflation and output, and raises the unemployment rate. I discuss the robustness of my results along several dimensions in Section 6. Section 7 concludes.
2. Biased Romer and Romer Estimates – The Role of Credit Spreads
To establish the arguments and mechanisms in this paper more clearly, I replicate a simple model of the economy from BT to outline how anticipatory monetary policy by an inflation-targeting central bank may bias our estimates of the effect of monetary policy on inflation, how the RR approach aims to address this, and under which conditions the RR approach fails to remove this bias.
2.1 Anticipatory Monetary Policy and the Price Puzzle
Assume inflation is determined as follows
and assume for simplicity that the cash rate affects inflation only through the observable determinant(s) of inflation Xt (e.g. unemployment or output as captured by a standard VAR model),
Here, is the rate of inflation in period t, rt is the cash rate announced in t, Zt – 1 is a variable (or vector of variables) that helps the central bank predict inflation but that is unobserved (or otherwise omitted from the model) by the econometrician, and and are unforecastable white noise innovations. The researcher then aims to estimate by running the simple regression:
The estimator is given by[7]
which will suffer from omitted variable bias if: (i) (the central bank responds to indicators not observed by the econometrician), and (ii) (these indicators have predictive information for inflation over and above what is captured in the researcher's model, here Xt – 1).[8]
Both conditions are likely satisfied. Central banks monitor a wider range of macroeconomic or financial indicators than included in a small-scale VAR. As a consequence, following Sims (1992), the literature typically adds additional ‘information’ variables such as commodity prices to the simple, small-scale monetary policy VAR models to better capture the central bank's forecasts. Commodity prices are posited to have additional predictive content for inflation , and as a result the central bank raises the policy rate in response . If , then and the price puzzle emerges. However, as shown by Hanson (2004), the additional predictive content of these variables in Zt – the basis on which they are included – is weak at best, and adding additional variables does not necessarily resolve the price puzzle.
But the Bank monitors a wider range of indicators than just commodity prices and also obtains unique information through its business liaison program. This vast amount of information helps the Bank predict inflation to an extent that alternative forecasts or simple models used by researchers usually cannot (Tulip and Wallace 2012). As evident from the Board minutes, this information also guides the Board's cash rate decisions. However, adding this broad range of indicators to the VAR model is not feasible without applying some dimension reduction technique.[9]
RR thus aims to remove the anticipatory component in policy rate changes by controlling directly for the central bank's (inflation) forecasts . A potential concern is that the central bank's forecasts take into account any planned changes to the cash rate. This motivates the use of short-term forecasts by RR and BT, given the likely longer lag with which the cash rate affects inflation and the high persistence of inflation. Assume for now that the forecast is produced by weighing information from Xt and Zt and under the assumption of a constant cash rate (or no feedback from the cash rate to the forecast). Following BT, I formalise this by assuming that Xt enters the forecast with a lag:
In the first step, the researcher estimates:
In the second step, the residual is then used as a proxy for the true monetary policy shock mt to estimate the effect of a cash rate change on inflation using a simple univariate regression[10]
The estimator of is then
which is unbiased because as the residual is orthogonal to the unobserved predictor Zt – 1 by controlling for the central bank's forecasts Ft – 1 at the time the cash rate was set.
2.2 Bias in the Romer and Romer Approach
The RR approach should be able to successfully remove any anticipatory component of monetary policy with respect to its inflation objective as long as the Bank's forecasts reflect all information that the Board's cash rate decision is based on. Importantly, the approach does not require the Board to only change the cash rate in response to the Bank's inflation forecast. If the Board changes the cash rate for reasons other than achieving its inflation target, these changes can be used as instruments for policy shocks with regard to inflation. The approach only requires that cash rate changes made in anticipation of inflation outcomes are based on the inflation forecast alone, and not on any other information.
These insights can be used to highlight how the RR approach may fail to remove the anticipatory component of monetary policy. The following assumptions may feel hypothetical for now, but I will argue later that they hold. Assume that Zt is a determinant of inflation as before (see Equation (1)), but it does not inform the Bank's central inflation forecast, that is
The cash rate still affects inflation only through Xt as before. While the Bank's forecasts do not incorporate the information in Zt, the Board nonetheless responds to this information, that is
This may reflect the fact that the Board views Zt as informative about the risks around the central forecast, and therefore responds to this information, or that the Board forms their own forecasts based on the central forecast produced by the Bank and the information contained in Zt.
Following the RR approach, the researcher omits this additional response to Zt when estimating
Accordingly, the obtained instrument for the policy shock is correlated with the information and another, plausibly exogenous shock in Zt thus violating the exogeneity condition of being a valid instrument for the true, unobservable policy shock mt (see, for example, Stock and Watson (2018) for a discussion). The first-stage estimator of is then given by
and is unbiased as long as the Bank's central forecast does not incorporate information from Zt, that is, . The researcher then estimates the effect of a cash rate change on inflation as
The estimator is given by
which is biased if (Zt is a determinant of inflation beyond what is captured in the central bank's forecasts through Xt) and (the cash rate responds to Zt over and above the central bank's forecasts).[11]
I will show that both of these conditions are likely fulfilled with Zt including credit risk spreads in money market or lending rates. The cash rate systematically responds to such spreads over and above the Bank's forecasts, and these spreads explain the Bank's forecast errors for inflation and the unemployment rate. Since the Board lowers the cash rate when credit spreads rise and higher spreads are associated with lower inflation than forecast , the bias will be positive . If the price puzzle emerges.
2.3 Narrative Evidence around the GFC
For an inflation-targeting central bank to adjust its policy rate but not its forecasts in response to information that has predictive content for inflation may appear surprising at first. But going back to the GFC episode may offer some support for this and provide some intuition for how it may lead to the emergence of the price puzzle found by BT.
During the GFC, the Bank paid particular attention to a wide range of financial market indicators. These indicators signalled in real time the sharp deterioration in financial market conditions around September 2008. This deterioration was driven by uncertainty about the passage of the Troubled Asset Relief Program (TARP) in the United States, the exposure of financial investors and intermediaries to the asset-backed securities market and the quality of the assets underpinning those securities (Debelle 2018). As a result, risk premia on money and fixed income markets rose sharply, reflecting increased risk aversion, greater uncertainty and liquidity hording of financial intermediaries and investors. Indicators such as spreads between corporate and government bond yields, money market risk premia and stock market volatility indices thus provided real-time signals about the stress on global financial markets at the time (Figure 2).
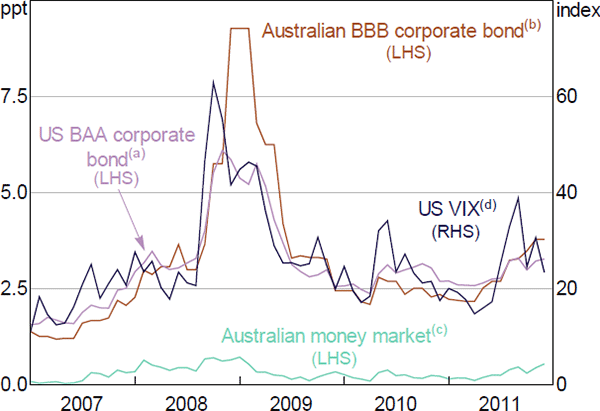
Notes:
(a) US BAA corporate to 10-year US Treasury bond yield
(b) Australian BBB corporate bond rate to 10-year Australian government bond yield
(c) Australian 3-month bank bill rate to zero-coupon yield
(d) Chicago Board Options Exchange, CBOE Volatility Index
Sources: Author's calculations; Federal Reserve Bank of St. Louis; RBA
The Reserve Bank Board responded decisively to this deterioration in global financial market conditions and cut the cash rate by a total of 275 basis points from October to December 2008. However, these cuts were not accompanied by marked changes to the forecasts. While the inflation forecasts remained largely unchanged over this period, the unemployment rate forecasts were revised upwards only in early 2009 after the cash rate had already been reduced by 300 basis points from its August 2008 level (Figure 3).
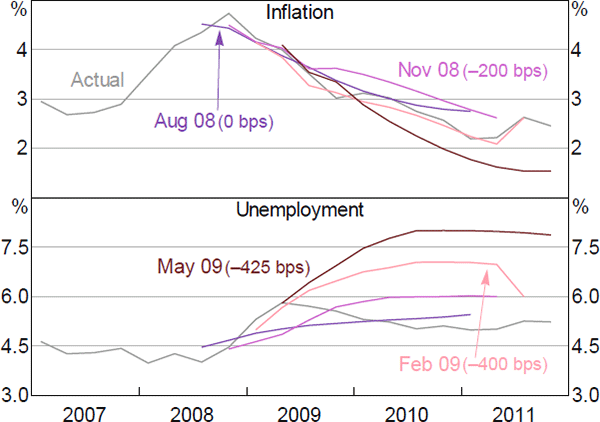
Notes: Forecasts of underlying inflation (year-ended) and the unemployment rate as published in the Statement on Monetary Policy (SMP ); cumulative cash rate changes since June 2008 in parentheses
Sources: ABS; Author's calculations; RBA
So why were the cash rate and the Bank's forecasts adjusted differentially in early 2009? The minutes of the Board meetings reveal that the sharp reductions in the cash rate over the last three months of 2008 were primarily a response to the sharply worsening conditions in international financial markets, the deterioration of the global outlook and the resulting increased downside risks for domestic growth and inflation (RBA 2008a, 2008b, 2008c). These developments were obviously not only observed by the Board but by the Bank's staff, too. Informing the Board's views, the Bank immediately lowered its outlook for output growth and raised its longer-term unemployment rate forecast in November 2008 (RBA 2008d). In contrast, the inflation forecast was initially revised upwards on the back of a strong depreciation of the exchange rate. However, the duration and extent of the global financial market turmoil and the weakness in global growth and its spillovers to the Australian economy were unclear at the time, especially given that most real economic indicators held up until around early 2009 (RBA 2009). Accordingly, the Bank staff did not centralise the information from financial market indicators into its forecasts, but assessed that they presented considerable downside risks to the outlook (RBA 2008d).[12]
For a researcher following the RR approach, the sharp reduction in the cash rate would hence appear as a large accommodative monetary policy shock given the lack of forecast adjustments. And as inflation eventually printed lower than forecast by the Bank, this decline in inflation would thus be attributed to the ‘surprise’ easing of monetary policy, thereby supporting a positive correlation between monetary policy changes and future inflation. As an isolated incident, this would unlikely be able to explain the price puzzle. But if this relationship was systematic, the policy shocks previously identified by BT would in fact be a mix of cash rate changes exogenous to the economic outlook and a systematic, endogenous response to changes in credit market conditions.
3. The Cash Rate Response to Credit Market Conditions
I first show that the cash rate systematically responds to changing credit and money market conditions. This addresses one of the two requirements for biased estimates by the RR approach discussed in the previous section. However, I will also show that it implies that the RR ‘shocks’ used by BT are anticipated as financial market participants understand and expect the Bank's response to financial market conditions. This adds a second, separate source of potential bias relating to the issue of non-fundamentalness when using these shocks as instruments for monetary policy shocks in SVARs (Leeper et al 2013; Ramey 2016).
3.1 A Taylor Rule Augmented with Credit Spreads
To quantify the response of the cash rate to credit and money market conditions, I follow RR and BT and estimate a standard forward-looking Taylor-type rule in differences augmented by credit spreads:
Here denotes the change in the cash rate at the Board meeting in month t, crt – 1 its level prior to the meeting, contains the Bank's h-quarter-ahead macroeconomic forecasts provided to the Board, and CSt includes one or more indicators from a set of money or credit market spreads or other financial market indicators available at the time of the meeting. The residual, , from this regression will then serve as the RR monetary policy shock.
While other specifications of the monetary policy reaction function are conceivable, I follow the exact specification of BT to allow direct comparison of my results with their findings.[13] Accordingly, includes the two-quarter-ahead forecasts for inflation , real GDP growth , the revisions to these forecasts since the previous forecast round , and the nowcast for the unemployment rate .[14] I estimate these policy rules on quarterly data over the inflation-targeting period from 1994:Q1 to 2018:Q4 using only Board meetings for which new forecasts are available.[15]
3.1.1 Measures of credit market conditions
I augment this benchmark rule using several measures capturing risk premia in money and credit markets and financial market uncertainty. As discussed in the previous section, these measures served as important real-time gauges for financial market stress during the GFC and informed monetary policy to a considerable extent. This has also motivated their extensive use in the literature to study the effect of credit supply shocks and interbank market disruptions on real economic activity.[16] For the United States, Caldara and Herbst (2019) have used the spread between the BAA corporate and 10-year Treasury bond yields to explore the role of credit market shocks for the identification of monetary policy shocks. Following this approach for Australia is unfortunately not possible as corporate bond spreads are only available from around 2004.
Thus, I use the alternative measures of credit risk and uncertainty shown in Figure 4. First, I also use the US BAA corporate to 10-year US Treasury bond yield spread and the US VIX to capture global risk aversion and credit supply shocks on US short-term debt funding markets that are important to Australian banks. As shown by Finlay and Jääskelä (2014) and Eickmeier and Ng (2015), US credit market shocks have strong spillover effects on Australian credit markets. Second, to capture changes to domestic credit market conditions, I use two measures of money market and lending rate spreads. The spread between the 3-month bank-accepted bill (BAB) rate and the 3-month Australian dollar overnight indexed swap (OIS) rate captures credit risk on the interbank market. However, the OIS rate is also only available from July 2001. For the earlier sample starting in 1994, I hence use the 3-month risk-free zero-coupon yield as estimated by Finlay and Olivan (2012) as the risk-free benchmark. Following Finlay and Jääskelä (2014), I further use the spread between the average large business variable lending rate and its reference rate, the 3-month BAB rate .[17] As expected, these spreads are strongly correlated with the Australian BBB corporate to 10-year Australian government bond yield spread over the common sample with a correlation of around 0.5 in levels and of 0.3 and 0.45 in differences. I account for the real-time availability of all financial market information by using the end-of-month value for the month prior to the Board meeting.
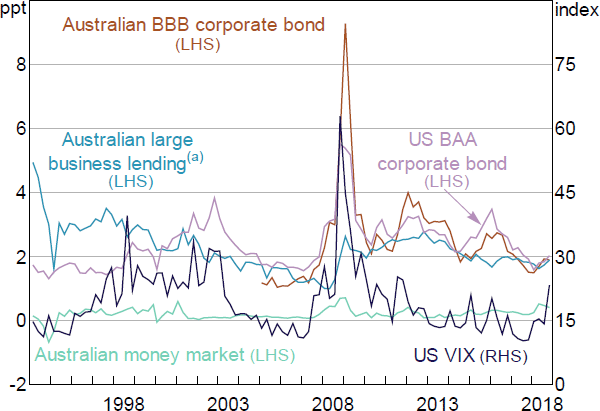
Notes:
As available at the beginning of forecast months (end-quarter months to 2000, mid-quarter months since); see Figure 2 for further notes
(a) Spread between Australian large business variable lending rate and 3-month bank bill rate
Sources: Author's calculations; Federal Reserve Bank of St. Louis; RBA
3.1.2 Estimation results
Similarly to the findings of Caldara and Herbst (2019) for the United States, I find a strong and economically significant response of the policy rate to credit market conditions (Table 1). On average, the Board aims to offset a bit more than half of any exogenous change to money market spreads ( , regression BT-CS1). The cash rate response to business lending spreads , US credit spreads and financial market uncertainty is also significant (regressions BT-CS2 to BT-CS4, respectively), similar to findings for the United States in Evans et al (2015) and Caggiano et al (2018). On average, a 100 basis point increase in the spread between business lending and the benchmark money market rate is met by a 18 basis point cut to the cash rate (regression BT-CS2). I also find that each of the three credit spread measures provides additional, unique information to the Board (regression BT-CS). While the estimated coefficients on domestic business lending spreads and the US corporate bond spread decline, they remain statistically significant at the 10 per cent level. The US VIX does not add additional information as soon as the US corporate bond spread is accounted for (not shown).
The responses to domestic money market and credit market spreads are not only statistically significant but also economically meaningful. Compared to the BT benchmark specification without any credit or money market spreads, my preferred specification (BT-CS) doubles the explanatory power of the model and now accounts for more than half of the total variation in cash rate changes. However, this does not result from materially changed responses to the Bank's forecasts. Similar to BT, I find that the Board reacts most strongly to revisions to the inflation and output forecasts .
| Variable | BT | BT-CS1 | BT-CS2 | BT-CS3 | BT-CS4 | BT-CS |
|---|---|---|---|---|---|---|
| Constant | −0.25 | 0.20 | −0.30* | 0.15 | −0.08 | 0.30* |
| ctt – 1 | 0.00 | 0.01 | −0.01 | 0.02 | 0.01 | −0.01 |
| 0.02 | −0.02 | −0.02 | −0.02 | −0.01 | 0.00 | |
| 0.08*** | 0.03 | 0.08*** | 0.04 | 0.05* | 0.02 | |
| −0.01 | −0.02 | 0.06** | −0.02 | −0.01 | 0.00 | |
| 0.21*** | 0.19*** | 0.16** | 0.16** | 0.22*** | 0.15** | |
| 0.07** | 0.06** | 0.08** | 0.07** | 0.08** | 0.07** | |
| −0.71*** | −0.60*** | |||||
| −0.18*** | −0.08* | |||||
| −0.18*** | −0.06* | |||||
| −0.01** | ||||||
| Observations | 100 | 100 | 100 | 100 | 100 | 100 |
| R 2 | 0.280 | 0.525 | 0.370 | 0.381 | 0.329 | 0.574 |
| Adjusted R 2 | 0.234 | 0.489*** | 0.322*** | 0.334*** | 0.278* | 0.532*** |
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively; for variable definitions and their sources, see Appendix C; statistical significance of the difference in model fit (Adjusted R 2) to the benchmark is assessed using a likelihood ratio test | ||||||
3.2 Is the Response to Credit Market Conditions Anticipated by Financial Markets?
The strong and consistent response of the cash rate to money and credit market risk spreads suggests that considerable profits could be made by predicting the Bank's response to money and credit market conditions, unless financial market participants are already aware of this systematic response. Inferring that this is not the case suggests that cash rate changes, even after accounting for the Bank's forecasts, are anticipated by financial market participants. As a result, the RR shocks used by BT would not qualify as valid instruments for true, unanticipated policy shocks and may give rise to the issue of non-fundamentalness when using them as instruments for shocks in a SVAR.
I address this question by adding financial market participants' expectations about the change in the cash rate over the next quarter to the RR regression in Equation (15).[18] After adding these expectations to the BT benchmark rule and the policy rule augmented by credit spreads (regressions BT and BT-CS of Table 1), all other coefficients in both policy rules are now close to zero and insignificant (Table 2, regressions BT-EXP and BT-CS-EXP). Only the coefficient on the expected cash rate is significant and positive as expected. This suggests that the Bank's policy reaction function – including the response to financial market conditions – is well understood and anticipated.[19]
| Variable | BT | BT-EXP | BT-CS | BT-CS-EXP |
|---|---|---|---|---|
| Constant | −0.25 | −0.04 | 0.30* | 0.02 |
| crt – 1 | 0.00 | 0.01 | −0.01 | 0.01 |
| 0.02 | 0.03 | 0.00 | 0.01 | |
| 0.08*** | 0.02 | 0.02 | −0.01 | |
| −0.01 | 0.00 | 0.00 | −0.02 | |
| 0.21*** | 0.04 | 0.15** | 0.03 | |
| 0.07** | 0.04* | 0.07** | 0.03 | |
| −0.60*** | 0.11 | |||
| −0.08* | 0.06* | |||
| −0.06* | −0.03 | |||
| 0.53*** | 0.59*** | |||
| Observations | 100 | 100 | 100 | 100 |
| R 2 | 0.280 | 0.763 | 0.574 | 0.773 |
| Adjusted R 2 | 0.234 | 0.753*** | 0.532 | 0.761*** |
| Notes: See notes for Table 1; statistical significance of the difference in model fit is assessed against either the BT or BT-CS benchmark model excluding cash rate expectations | ||||
These findings thus suggest that the residual obtained from the BT regression not only includes a systematic response to credit market conditions but is also predictable using financial markets' expectations about future cash rate changes. This can further be seen by regressing this residual on the expected cash rate change prior to the Board meeting:
I find that expected cash rate changes explain around half of the variation in the residuals from the original Bishop and Tulip (2017) regression and predict these residuals with a slope coefficient of 0.29 (Figure 5; Table 3). In contrast, expected cash rate changes explain only around 10 per cent of the variation in the residuals from the augmented BT-CS regression. However, the positive and significant relationship between expected cash rate changes and both the BT and the BT-CS residuals questions their suitability as shocks reflecting a structural disturbance (Ramey 2016; Stock and Watson 2018).[20] I will thus purge the residuals from the augmented model (BT-CS) of this additional anticipatory component when constructing the monetary policy shock series in Section 5.
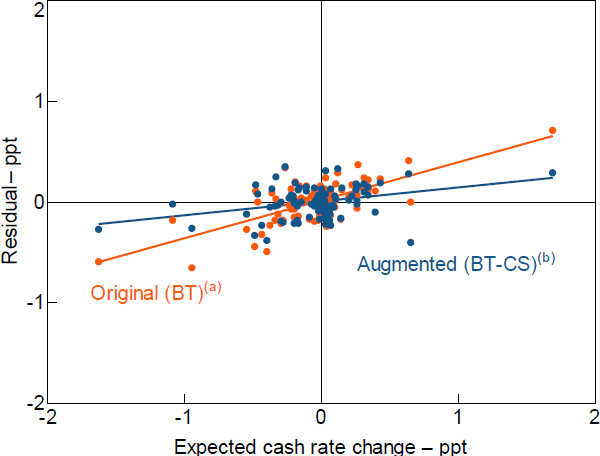
Notes:
Lines of best fit from Equation (16)
(a) Residuals from regression BT of Table 1
(b) Residuals from regression BT-CS of Table 1
| Variable | BT | BT-CS |
|---|---|---|
| Constant | 0.02 | 0.01 |
| 0.29*** | 0.12*** | |
| Observations | 100 | 100 |
| R 2 | 0.473 | 0.134 |
| Notes: Dependent variables are residuals from regressions BT and BT-CS of Table 1; see Table 1 for further notes | ||
4. Credit Market Conditions and the Bank's Forecast Errors
The previous section has shown that the cash rate responds strongly to money and credit market conditions. If these conditions ease and credit intermediation and credit supply to the real economy increases, the cash rate increases. Hence, the first condition for the proposed explanation for the price puzzle is fulfilled. However, for this relationship to explain the price puzzle, easy credit market conditions also need to provide additional information about higher future inflation over and above what is captured in the Bank's forecasts for inflation.
I will test whether the financial market indicators used in the previous section systematically explain the Bank's inflation forecast errors. However, to shed light on any differential effects of monetary policy on inflation, output and unemployment as later estimated using the original BT or the new credit spreads-augmented (BT-CS) monetary policy shock series, I will test for efficiency of the Bank's forecasts for all of these three variables, that is
where is the forecast error of annualised underlying inflation, the unemployment rate, or annualised real GDP growth. I define the forecast error of the forecast made in period t and realised in period t + h as . A positive error for inflation thus means that inflation printed higher than forecast by the Bank. I regress this error on previous errors as available when the forecast was made and on each of the financial market indicators separately. I also include past lags of quarterly inflation, output growth and the change in the unemployment rate in the vector Zt – 1. Throughout, I account for the real-time availability of the data as much as possible.[21]
4.1 Inflation Forecast Errors
In line with the Board's response to domestic money and credit market spreads, I find that both these spreads explain the Bank's forecast errors for inflation to a considerable extent and in the expected direction (Table 4, columns (2), (3) and (6)). Easier domestic credit market conditions (lower spreads) predict inflation to print higher than forecast by the Bank. While the coefficient on the business lending spread is no longer statistically significant when jointly added with the money market spread, the overall explanatory power increases to 20 per cent compared to 12 per cent for the model only including money market spreads. In contrast, the US corporate bond spread and the US VIX provide little predictive information for inflation over and above the Bank's forecasts (columns (4) and (5)). Similarly, the Bank's forecasts also make efficient use of past forecast errors and all available macroeconomic data captured in the controls. Finally, the results are strongest in terms of marginal predictive power for the one-year horizon but also hold to a similar degree for horizons from two quarters onwards (see Table D2).[22] In conclusion, both conditions explaining why the RR approach delivers the price puzzle are fulfilled.
| Predictor | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| Constant | −0.35 | −0.18 | 0.37 | −0.12 | −0.27 | 0.44 |
| 0.40 | 0.46 | 0.34 | 0.41 | 0.41 | 0.39 | |
| −0.08 | 0.00 | −0.01 | −0.01 | −0.08 | 0.05 | |
| 0.11 | 0.08 | 0.12 | 0.09 | 0.11 | 0.10 | |
| −0.84** | −0.65** | |||||
| −0.33* | −0.29 | |||||
| −0.09 | ||||||
| −0.01 | ||||||
| Observations | 91 | 91 | 91 | 91 | 91 | 91 |
| R 2 | 0.077 | 0.124** | 0.172*** | 0.089 | 0.081 | 0.199*** |
| F-statistic | 0.98 | 1.46 | 2.12** | 1.00 | 0.90 | 2.24** |
| Notes: The regression includes four lags of the dependent variable (not shown); statistical significance of the marginal predictive power (difference in R 2) of credit market indicators relative to the benchmark model (regression (1)) is assessed using a likelihood ratio test; joint significance of all predictors (including AR terms) is assessed using an F-test; see Table 1 for further notes | ||||||
4.2 Unemployment and GDP Forecast Errors
Since money and credit market conditions provide additional information about future inflation, it is reasonable to expect this to be the case for other variables that the Bank may target. This is particularly the case since the Bank's forecasts for inflation are informed by forecasts for a range of indicators, most importantly the unemployment rate as an indicator of labour market tightness (Ballantyne et al 2019).
However, I find little evidence that credit market indicators provide additional information for the unemployment forecast (Table 5). I show the results for all horizons for the specification including both domestic credit market measures only: as a) these measures predict inflation, and b) these measures are most important for explaining any cash rate changes.[23] The coefficients on both credit market indicators are insignificant throughout, and with the exception of the two-year horizon they do not improve the model fit significantly. In contrast, there is some evidence that the spread between business lending rates and the money market rate can provide additional predictive information for GDP forecasts over the short- to medium-term horizons (Table 6). However, the coefficients are positive which is surprising and at odds with the findings in the literature (i.e. Gilchrist and Zakrajšek (2012) and López-Salido et al (2017), and – to the extent that credit spreads may capture sentiment or risks around the Bank staff's central forecasts – also Sharpe et al (2017)). Thus, my results suggest that tighter credit conditions are associated with lower inflation (as expected) but higher economic growth than forecast. Reconciling these conflicting findings is difficult and left to future research.[24]
| Predictor | Horizon (in quarters) | ||||
|---|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 8 | |
| Constant | −0.33*** | −0.27* | −0.57*** | −0.42 | −2.08*** |
| 0.32* | 0.27* | 0.49* | 0.50* | −0.05 | |
| −0.34** | −0.34** | −0.43 | −0.26 | −0.92* | |
| −0.07 | −0.13*** | −0.06 | −0.08 | 0.32*** | |
| 0.12 | 0.04 | −0.24 | −0.86** | 0.33 | |
| 0.01 | −0.03 | −0.03 | −0.06 | 0.70 | |
| Observations | 96 | 95 | 91 | 87 | 70 |
| R 2 | 0.368 | 0.187 | 0.190 | 0.197 | 0.264** |
| Note: See notes for Table 4 | |||||
| Predictor | Horizon (in quarters) | ||||
|---|---|---|---|---|---|
| 1 | 2 | 4 | 6 | 8 | |
| Constant | −1.26*** | −1.61*** | −2.12*** | −0.88* | 2.43*** |
| −0.08 | 0.10 | 0.10 | 0.22 | 0.41 | |
| 1.07** | 1.34** | 0.49 | 0.47 | −0.92* | |
| −0.49** | −0.49*** | 0.04 | −0.07 | −0.38* | |
| 1.44 | 1.12** | −0.18 | −0.54 | −1.29 | |
| −0.13 | 0.18* | 0.87 | 1.00*** | 0.11 | |
| Observations | 96 | 95 | 91 | 87 | 71 |
| R 2 | 0.401** | 0.242 | 0.238*** | 0.206*** | 0.198 |
|
Note: See notes for Table 4 |
|||||
For the following analysis on the role of credit market conditions for resolving the price puzzle, however, both necessary conditions are fulfilled. The Bank raises the cash rate as credit conditions ease, and easier credit conditions predict inflation to print higher than forecast by the Bank. These relationships are also in line with credit supply shocks being key drivers of the business cycle (Gilchrist and Zakrajšek 2012; López-Salido et al 2017), and the Board responding to this information over and above the Bank's forecasts (Evans et al 2015; Adrian and Duarte 2016; Caggiano et al 2018; Caldara and Herbst 2019). As credit conditions have less predictive content for unemployment and GDP over and above the Bank's forecasts, my results are less likely to explain any potential biases in the estimated responses of these variables.
5. The Effects of Monetary Policy Shocks on Inflation, Unemployment and Output
The results from the previous sections suggest that RR shocks used by BT are invalid instruments for truly exogenous monetary shocks for two reasons. First, they violate the exogeneity condition as they capture the Bank's endogenous response to credit market spreads motivated by the predictive information for inflation in those spreads. Second, they are anticipated by financial market participants and hence give rise to the issue of non-fundamentalness in SVAR models.
I will explore the relevance of these two issues in turn. In the first step, I will assess the effects of monetary policy when estimated using the residuals from the Taylor-type policy rule augmented by credit spreads (regression BT-CS of Table 1) as my monetary policy shock series. These ‘first-stage’ residuals are independent of the Bank's response to financial market conditions but are still anticipated to some extent as shown in Section 3.2 (Table 3; Figure 5). In the second step, I will then remove this anticipatory component from these ‘first-stage’ residuals by purging them of the expected cash rate change by financial market participants (Table 3).
At each step, I will estimate the effects of monetary policy on the variables of interest in a simple SVAR with four lags similar to RR, Coibion (2012) and BT. Accordingly, the VAR includes (log) underlying CPI, (log) real GDP, the unemployment rate and a measure of the policy shock, in that order. Here, the policy shock replaces the cash rate typically included to measure the stance of monetary policy. Since the cash rate is typically included in levels, I cumulate the quarterly shock series over time. The ordering imposes the typical recursive identifying assumption that changes in the policy rate do not affect any macroeconomic variables within the same quarter.[25]
5.1 Accounting for the Cash Rate Response to Credit Conditions
Accounting for the cash rate's response to domestic and international money and credit market spreads has a marked effect on the residuals from Equation (15) – the policy shock series (Figure 6). The residuals from the original BT specification follow actual cash rate changes closely with a correlation of around 0.86, reflecting the low model fit of the regression. In contrast, the correlation between the residuals of the credit spreads-augmented model (BT-CS) with actual policy changes is considerably weaker (0.67).
Most visibly, the response to credit spreads helps to explain the large cash rate changes in the mid 1990s and around the GFC. Whereas the BT specification attributes policy shocks to be the most important source of these changes, the credit spreads-augmented model interprets only around one-fourth of them to be a policy shock independent of the Bank's usual reaction to its forecasts and to credit market conditions. But it is not only large cash rate changes for which the size and direction of the shock differs between the two models. For example, the residual of the augmented model frequently differs in sign from the actual cash rate change and the BT residual, in particular over the tightening cycle prior to the GFC.
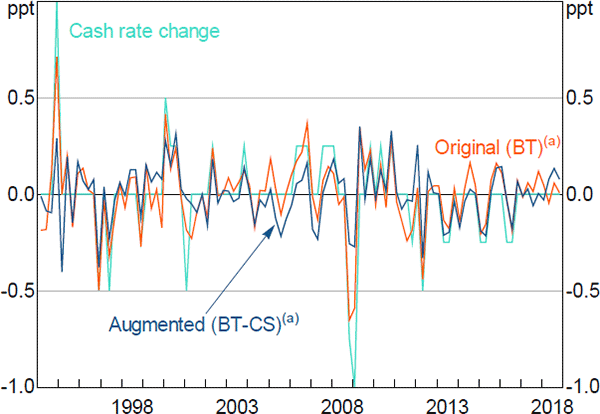
Note: (a) Monetary policy shocks are residuals from quarterly regressions BT and BT-CS of Table 1
These differences in the residual series have strong implications when using them to estimate the effects of monetary policy on the Bank's target variables. Most importantly, there is no evidence for the price puzzle when using the credit spreads-augmented policy shock series (Figure 7, upper right panel). Using the new augmented BT-CS series suggests that prices fall by around 0.15 per cent over six quarters, but the estimated response is subject to considerable uncertainty and not statistically significant.[26] This is nonetheless in stark contrast to the original BT shock series which suggests that a contractionary policy shock of 100 basis points raises inflation immediately and lifts the price level for a prolonged period of time with a peak effect of around 1 per cent after two years (upper left panel).
In contrast to the response of prices, the estimated effects of monetary policy on the unemployment rate and real GDP are largely unchanged when using the new credit spreads-augmented policy shock series (Figure 7, middle and lower panels). However, some features are worth highlighting. First, using the new credit spreads-augmented BT-CS model residuals as the policy shock, the initially negative unemployment response (the ‘unemployment puzzle’) is now smaller and not statistically significant, and unemployment starts to increase sooner compared to estimates using the original BT residual. These estimates suggests that the unemployment rate peaks around 1/3 of a percentage point higher around six quarters after the shock. The effects on real GDP are also slightly more contractionary with output falling by around 1 per cent over the first year.
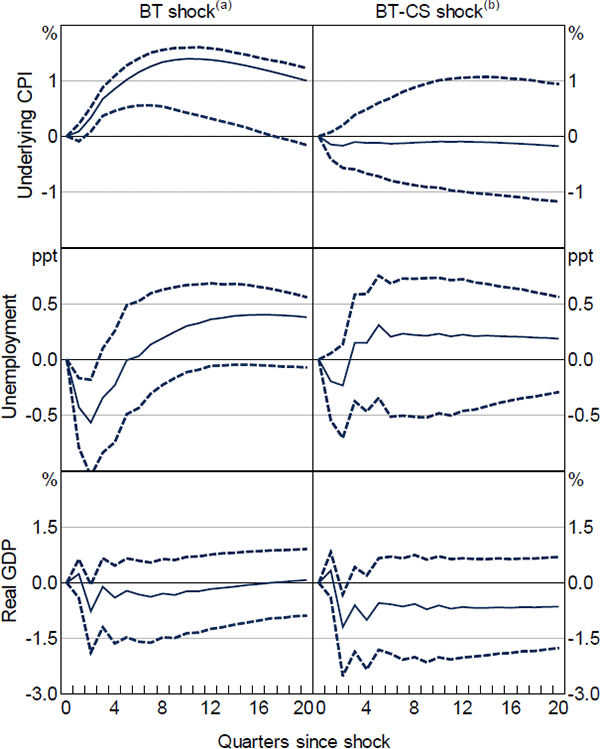
Notes:
See notes for Figure 1
(a) Bishop and Tulip ((2017), updated) policy shock; residuals from regression BT of Table 1
(b) BT shock accounting for cash rate response to credit spreads; residuals from regression BT-CS of Table 1
5.2 Unanticipated Monetary Policy Shocks
As predicted by the theoretical considerations in Section 2 and the empirical results in Sections 3 and 4, the price puzzle found by Bishop and Tulip (2017) can be explained to a considerable extent by accounting for the systematic response of the cash rate to financial conditions. However, as shown in Section 3.2, the residual of the credit spreads-augmented model (BT-CS) is still anticipated to some extent by financial market participants and hence is not a valid instrument for monetary policy shocks (Ramey 2016; Stock and Watson 2018; Miranda-Agrippino and Ricco 2018). Therefore, I follow Miranda-Agrippino and Ricco (2018) and purge the BT and BT-CS residuals of financial market participants' expectations of the cash rate change ahead of the Board meeting.[27]
Reflecting the considerable explanatory power of expected cash rate changes for the original BT residuals (Table 3), the purged BT shocks differ considerably from the original shocks (Figure 8, upper panel). This is in line with the previous findings that expectations of cash rate changes – after accounting for the Bank's forecasts – are largely driven by the expected cash rate response to financial market conditions (Table 2). As a result, the unanticipated BT shock series now resembles the BT-CS residuals more closely. In contrast, purging the BT-CS residual of financial market expectations makes little difference, with the exception of the GFC episode (Figure 8, lower panel).
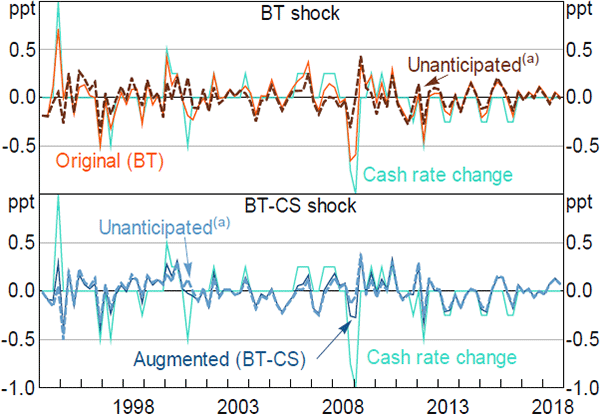
Note:
Notes: See notes for Figure 6
(a) Shows monetary policy shocks purged of the expected cash rate change ahead of the Board meeting
Accordingly, this additional step of removing financial markets' expectations of future cash rate changes from the credit spreads-augmented policy shock series only marginally changes my main results. As before, raising the cash rate lowers inflation and output, and raises the unemployment rate (Figure 9, right panels). However, using this new policy shock series which is both unanticipated and takes into account the Bank's response to credit market conditions suggests slightly stronger contractionary effects of a cash rate change compared with the anticipated BT-CS shock. I now find prices to fall by around 0.7 per cent after around two years before slowly returning to their pre-shock levels. Likewise, the unemployment rate now remains flat for the initial few quarters after the shock before increasing by around 1/3 of a percentage point after six quarters. The output response is largely unchanged.
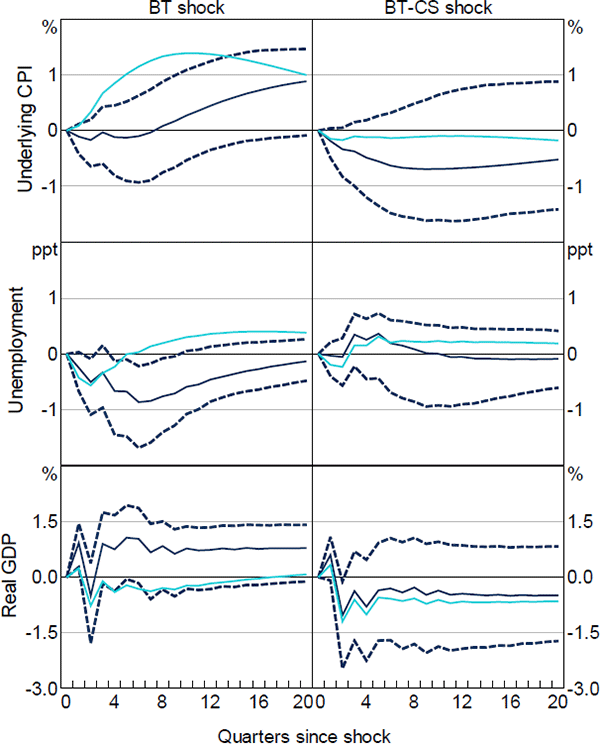
Notes: Dark solid (and dashed) lines show the responses (confidence intervals) to the unanticipated BT and BT-CS shocks; light solid lines show responses to original BT and BT-CS shocks shown in Figure 7; for further notes see Figure 7
This is in stark contrast to the original BT shock (Figure 9, left panels). Here, removing financial market expectations from the anticipated shock series makes a strong difference. While removing financial market expectations from the shock removes the price puzzle for the first two years after the shock, inflation nonetheless appears to increase in the long run. Furthermore, the unemployment puzzle is now more pronounced, with unemployment falling by around 1 percentage point over the first two years and only slowly returning to its pre-shock level. This comes on the back of an economic boom with real GDP increasing by around 1 per cent. Overall, the responses of all macroeconomic variables are as implausible as the estimates obtained using the original BT shock.
These results suggest that purging cash rate changes only of the Bank's forecasts and financial market expectations does not yield valid policy shocks, but that it is crucial to explicitly control for the cash rate's systematic response to credit and money market conditions. Once both issues are taken into account, I obtain plausible estimates for the effects of a cash rate change on inflation, the unemployment rate and output. My preferred estimates from the unanticipated, credit spreads-augmented (BT-CS) policy shock are about twice as large for inflation, but otherwise closely in line with the dynamic responses of these variables to a cash rate shock as implied by MARTIN, the Bank's macroeconometric model.
6. Robustness to Model Misspecification and the GFC Episode
I find my results to be robust along several dimensions. In the following, I will highlight two main findings relating to model misspecification and the sensitivity of my results to the GFC episode. I discuss further robustness exercises in Appendix D. Throughout, I will focus on the effects on inflation and the unemployment rate since the response of real GDP is unchanged.
6.1 Model Misspecification – The Role of Financial Variables for Policy Transmission
An alternative explanation for the emergence of the price puzzle is that the SVAR model is misspecified. One possibility highlighted by Caldara and Herbst (2019) and Gertler and Karadi (2015) is that credit spreads may not only be an important omitted variable in the central bank's reaction function, but also an important channel for the transmission of monetary policy typically omitted from the VAR model. To test this explanation, I add the domestic money market and large business lending spreads to the SVAR model. Here, I compare the results from a VAR including the original, anticipated RR shock used by BT to one using my new preferred, unanticipated shock series. I order both variables after the policy shock so that they may respond instantaneously to a change in the cash rate. For the BT shock series this also retains the assumption that the cash rate does not respond to credit conditions instantaneously, while the new preferred shock series is already purged of this contemporaneous response. While adding domestic money and credit spreads to the baseline SVAR including the BT shock series removes the price puzzle in the long run, it cannot explain the initial emergence of the price or unemployment puzzles (Figure 10, left panels). In contrast, the results using the new preferred, unanticipated shock are little changed (right panels).
As discussed in Appendix D, I find my results to also be robust to a range of other SVAR specifications, and when estimating the effects of a cash rate change on inflation and unemployment using the univariate LP framework by Jordà (2005).
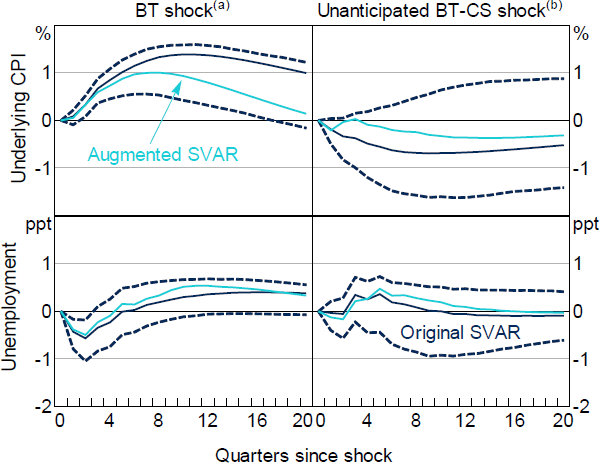
Notes:
Responses from baseline SVAR (dark solid and dashed lines, see Figure 1 for further notes) and SVAR augmented by money market risk spread and large business lending rate spread (lighter solid lines)
(a) Original, anticipated policy shock used by Bishop and Tulip ((2017), baseline SVAR responses as shown in left panels of Figure 7)
(b) New, unanticipated policy shock purged of the response to credit spreads (baseline SVAR responses as shown in right panels of Figure 9)
6.2 Excluding the GFC and Sub-sample Evidence
Since most of the variation in both cash rate changes and credit spreads occurred during the GFC, a natural question to ask is if my results are driven purely by this episode. This is not the case.
First, the cash rate response is largely robust to including a GFC dummy that takes the value of 1 for the four quarters from 2008:Q3–2009:Q2 or dropping this episode from the sample (Table 7). The only exception to this is the response to US corporate bond spreads which is no longer significant. This suggests that the cash rate responded to US financial market conditions only, or more strongly, during the GFC, possibly picking up the sharp spike in Australian corporate bond spreads not included in the model. The policy reaction function also appears largely robust over various sub-samples. Here, the only the exception is the response to large business lending spreads which appears to have increased (in the admittedly short sub-sample) since the GFC.
| Variable | GFC dummy | Excluding GFC | Pre-GFC | Post-GFC |
|---|---|---|---|---|
| −0.49*** | −0.48*** | −0.54*** | −0.47 | |
| −0.09* | −0.08* | −0.15* | −0.33** | |
| −0.04 | −0.05 | −0.09* | 0.02 | |
| −0.26** | ||||
| Observations | 100 | 96 | 62 | 38 |
| R 2 | 0.575 | 0.447 | 0.635 | 0.414 |
| Adjusted R 2 | 0.527*** | 0.390*** | 0.572*** | 0.225* |
| Notes: See notes for Table 1; all models include a constant and the set of forecasts as in Table 1; ‘Excluding GFC’ excludes 2008:Q3–2009:Q2, ‘Pre-GFC’ uses 1994:Q1–2008:Q2, ‘Post-GFC’ uses 2009:Q3–2018:Q4; statistical significance of the difference in model fit is assessed against the BT benchmark model over the same sub-samples (not shown) | ||||
Second, the predictive ability of domestic money and credit market spreads for the Bank's inflation forecast errors is also not exclusively driven by the GFC episode (Table 8). However, since the GFC the predictive information in credit spreads over and above what is already captured in the Bank's forecasts appears to have declined. This may be driven by two explanations. First, the sample is admittedly very small, and hence this result may reflect the lack of power of the forecast efficiency test. Second, it may also reflect learning by the Bank. As the GFC highlighted the importance of a smooth functioning of credit markets for the real economy, credit spreads arguably received stronger attention in the aftermath of the crisis. This may be reflected either in better forecasts by the Bank or a stronger response of the cash rate to offset any macroeconomic effects of changes in domestic credit market conditions as shown in Table 7.
| Predictor | GFC dummy | Excluding GFC | Pre-GFC | Post-GFC |
|---|---|---|---|---|
| Constant | 0.47* | 0.39 | 1.20*** | −0.76 |
| 0.37 | 0.55 | 0.11 | −0.37 | |
| 0.02 | −0.09 | 0.06 | 0.40 | |
| 0.10 | 0.12 | 0.07 | −0.24** | |
| −0.73 | −0.73* | −0.18 | 0.15 | |
| −0.30 | −0.33* | −0.53 | 0.29 | |
| 0.14 | ||||
| Observations | 91 | 80 | 51 | 29 |
| R 2 | 0.200*** | 0.226*** | 0.344*** | 0.531 |
| F-statistic | 2.01** | 2.27** | 2.39** | 2.39* |
| Notes: ‘Excluding GFC’ excludes 2008:Q3–2009:Q2, ‘Pre-GFC’ uses 1994:Q1–2008:Q2, ‘Post-GFC’ uses 2009:Q3–2018:Q4; see Table 4 for further notes; statistical significance of the marginal predictive power relative to the baseline model (not shown) is assessed over the same sub-samples | ||||
As a result, the estimated effects of monetary policy are also largely robust to excluding the GFC episode (Figure 11). However, while inflation shows the expected response throughout, the unemployment rate appears to fall in the long run. This is likely due to the considerable estimation uncertainty associated with long-run estimates from the LP framework used here. I exclude the GFC from both the first-step estimation of the RR regression and from the second-step LP regression. See Appendix D for further specifications of the LP regression.
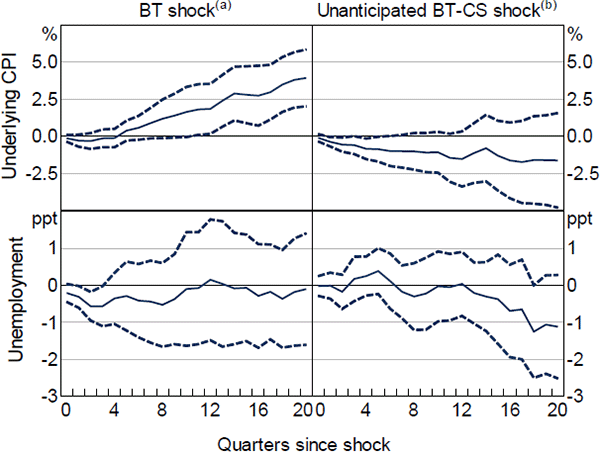
Notes:
Dashed lines show 90% heteroskedasticity and autocorrelation robust confidence intervals; 1994:Q1–2018:Q4, excluding 2008:Q3–2009:Q2
(a) Original, anticipated policy shock used by Bishop and Tulip (2017)
(b) New, preferred unanticipated policy shock
7. Conclusion
There is considerably uncertainty about the extent to which monetary policy affects economic activity and inflation. Indeed, previous empirical work has even provided estimates that are at odds with the Bank's view and standard macroeconomic theory about the direction of these effects. In response to an increase in the cash rate, inflation has been found to rise. This if often explained by an anticipatory component of monetary policy. Inflation does not rise in response to an increase in the cash rate, but the Bank raises the cash rate in anticipation of higher inflation.
In this paper, I show that the failure of standard estimates to account for this anticipatory component of policy is driven by an omitted systematic response of the cash rate to money and credit market conditions. When these conditions ease, the Bank raises the cash rate. As easier credit conditions raise economic activity and inflation, the increase in inflation is then falsely attributed to the increase in the cash rate. Controlling for the Bank's forecasts does not remove this bias as these forecasts do not fully capture the inflationary effects of changing credit conditions. Since easier credit market conditions systematically predict inflation to print higher than forecast by the Bank, the price puzzle emerges even after purging cash rate changes of the Bank's own inflation forecasts.
I show that it is therefore crucial to account for the response of monetary policy to credit market conditions when estimating its inflation effects. Furthermore, it is important to account for cash rate changes expected by financial market participants. Purging cash rate changes of the Bank's response to its forecasts and to several money and credit market spreads and of financial markets' expectations of future cash rate changes provides monetary policy shocks that are unanticipated and exogenous to the inflation outlook. Using these shocks, I find the expected effects of monetary policy. An increase in the cash rate lowers inflation and raises the unemployment rate.
Appendix A : Literature Review
For Australia, early research finds mixed evidence for the response of prices to monetary policy (no price puzzle in Dungey and Pagan (2000); Berkelmans (2005); price puzzle in Suzuki (2004); Beechey and Österholm (2008); Lawson and Rees (2008)). Brischetto and Voss (1999) find that controlling for US interest rates and the Australian dollar exchange rate is crucial to remove the price puzzle. Using more recent data, Jacobs and Rayner (2012) and Phan (2014) find strong price puzzles even in similar (successful) specifications to the earlier Australian research. This has raised the question whether identification of the effects of monetary policy in Australia has become more difficult since the advent of inflation targeting in the early 1990s. Using a simulation study, Jääskelä and Jennings (2010) find that standard identification schemes typically deliver a price puzzle and hence suggest using a sign-restriction identification approach which delivers the desired response by construction. Most recently, Hartigan and Morley (2018) propose that the price puzzle can be resolved using a factor augmented VAR (FAVAR), which better accounts for the vast information the Bank uses when producing its forecasts.
| Paper | Method and sample | Price puzzle | Peak/trough response | Discussion |
|---|---|---|---|---|
| Brischetto and Voss (1999) | SVAR(6), 7-variate, zero restrictions motivated by theory, 1980:Q1–1998:Q4 | No (in preferred specification), response not significant | Price level: 0.12%, 2 qtrs / –0.8%, 10 qtrs | No price puzzle only when allowing for contemporaneous response of the cash rate to US federal funds rate and to nominal AUD/USD exchange rate |
| Dungey and Pagan (2000) | SVAR(3), 11-variate, selected lags, zero restrictions motivated by theory, 1980:Q1–1998:Q3 | No | Inflation: –0.1 ppt, 10 qtrs (1 standard deviation shock) Price level: trough after 18 qtrs, magnitude unclear | |
| Suzuki (2004) | SVAR(2), 11-variate, recursive, 1985:Q1–2000:Q2 | Yes | Price level: 0.2%, 3 qtrs | Small price puzzle in unrestricted model, strong and significant puzzle in restricted model |
| Berkelmans (2005) | SVAR(3), 7-variate, zero restrictions motivated by theory, 1983:Q4–2003:Q4 | No | Inflation: –0.2 ppt, 12 qtrs | |
| Beechey and Österholm (2008) | Bayesian SVAR(3), 7-variate, recursive, 1985:Q1–2006:Q3 | Yes | Inflation: 0.1 ppt, 4 qtrs / –0.1, 10 qtrs | |
| Lawson and Rees (2008) | Sectoral SVAR(3), 11-variate, zero restrictions motivated by theory, 1983:Q4–2007:Q3 | Yes, insignificant | Inflation: 0.06 ppt, 3 qtrs / –0.5 ppt, 8 qtrs | |
| Jääskelä and Jennings (2010) | SVAR, 7-variate, sign restrictions, 1984:Q1–2009:Q4 | No, by construction | Inflation: –0.3 ppt, impact | |
| Jacobs and Rayner (2012) | SVAR(2), 11-variate, 1983:Q4–2011:Q4 | Yes, significant | Inflation: 0.05 ppt, 5 qtrs | Price puzzle becomes insignificant if a measure of inflation expectations is added |
| Phan (2014) | SVARs, various specifications, recursive, 1982:Q3–2007:Q4 | Yes, significant | Price level: 0.2–0.4%, 6 qtrs | |
| Bishop and Tulip (2017) | Univariate models and SVARs, various specifications, Romer and Romer (2004) identification, 1994:Q2–2015:Q4 | Yes | Price level: 0.5–1.5%, 8 qtrs | |
| Kim and Lim (2018) | SVAR(6), 6-variate, sign restrictions, 1993:Q1–2014:Q3 | No, by construction | Price level: –0.1%, 3 qtrs | |
| Florio (2018) | SVAR(1), 3-variate, recursive, 1976:Q3–2007:Q4 | Yes, significant | Price level: 0.7%, 10 qtrs | Significant price puzzle pre-inflation targeting, insignificant but equally strong thereafter |
| Hartigan and Morley (2018) | FAVAR(2), recursive, 1976:Q4–2017:Q2 | No | Inflation: 0.3 ppt, 10 qtrs Price level: 6%, 36 qtrs | |
| Notes: Peak and trough effects are to a 1 percentage point monetary policy shock, where provided by the author(s); effects are often approximated from graphical display of estimated effects; the shock is always contractionary and temporary, but the cash rate evolves endogenously after the shock and persistence may vary | ||||
Appendix B : Derivation of Estimators
Model:
OLS estimation equation:
OLS estimator:
Romer and Romer estimation:
First-stage:
Second-stage:
Romer and Romer estimator:
From Equation (B5)
Appendix C : Variable Definitions
| Variable | Definition | Source |
|---|---|---|
| crt | Cash rate set at Board meeting in month t | Reserve Bank of Australia (RBA) |
| Cash rate change at Board meeting in month t | RBA | |
| h-quarter-ahead forecast for annualised underlying inflation prior to Board meeting in month t | RBA | |
| h-quarter-ahead forecast for annualised real GDP growth prior to Board meeting in month t | RBA | |
| Revisions to inflation forecast h-quarter-ahead since previous Board meeting | RBA | |
| Revisions to real GDP forecast h-quarter-ahead since previous Board meeting | RBA | |
| h-quarter-ahead forecast for unemployment rate prior to Board meeting in month t | RBA | |
| Money market spread between 3-month bank-accepted bill (BAB) rate and 3-month Australian dollar overnight indexed swap (OIS) rate (3-month zero-coupon forward rate prior to July 2001); end-month value of month prior to Board meeting | RBA statistical tables: F1 Interest Rates and Yields – Money Market; F1.1 Interest Rates and Yields – Money Market Historical data: F17 Zero-coupon Interest Rates – Analytical Series – 1992 to 2008 |
|
| Credit market spread between average large business variable lending rate and 3-month BAB rate; end-month value of month prior to Board meeting | RBA statistical tables: F1; F1.1; F5 Lending Rates | |
| Moody's seasoned BAA corporate bond yield relative to yield on 10-year Treasury constant maturity, obtained from FRED; end-month value of month prior to Board meeting | Federal Reserve Bank of St. Louis, FRED database (Identifier ‘BAA10Y’) | |
| US VIX, obtained from FRED; end-month value of month prior to Board meeting | FRED database (Identifier ‘VIXCLS’) | |
| GFC dummy taking the value of 1 for all quarters from 2008:Q3–2009:Q2 | ||
| Expected cash rate change h-quarters-ahead obtained from zero-coupon yield curve as estimated by Finlay and Olivan (2012); end-month value of month prior to Board meeting | RBA statistical table: F1 Historical data: F17 | |
| US federal fund rate, obtained from FRED; end-month value of month prior to Board meeting | FRED database (Identifier ‘FEDFUNDS’) | |
| ntwit | Nominal trade-weighted exchange rate; end-month value of month prior to Board meeting | RBA statistical table: F11.1 Exchange Rates |
| RBA Index of Commodity Prices, $A All Items; end-month value of month prior to Board meeting | RBA statistical table: I2 Commodity Prices |
Appendix D : Further Robustness Tests and Results
D.1 SVAR Misspecification
In addition to adding domestic and credit market spreads to the baseline SVAR, I find my results to be robust to other SVAR specifications (Figure D1). These are: (i) choosing shorter or longer lag orders for the VAR (2 or 8 lags); (ii) ordering the policy shock first; and (iii) augmenting the SVAR by the Bank's commodity price index (in logs), the nominal trade-weighted exchange rate index (nominal TWI, in logs), and the US federal funds rate (Jacobs and Rayner 2012). Ordering the policy shock first allows monetary policy to have immediate effects on all endogenous variables in the VAR and reflects that the obtained policy shock series should already be exogenous to the state of the economy to the extent that this is captured by the Bank's forecasts. The SVAR with the policy shock ordered first and the augmented SVAR suggest slightly larger price effects, while both the augmented SVAR and a SVAR with longer lags suggest larger peak unemployment effects.
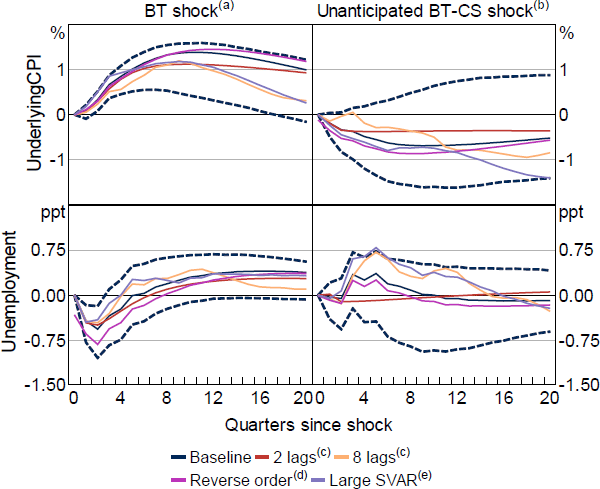
Notes:
See notes for Figures 7 and 9
(a) Original, anticipated policy shock used by Bishop and Tulip (2017)
(b) New, preferred unanticipated policy shock
(c) Baseline SVAR with 2 or 8 lags
(d) Cumulative policy shock ordered first
(e) Baseline SVAR augmented by RBA index of commodity prices, US federal funds rate and the Australian nominal TWI; nominal TWI ordered last
I further find my results to be largely robust when estimating the effects of a cash rate change using the univariate LP framework introduced by Jordà (2005).[28] Here, impulse responses are obtained by estimating the effects of monetary policy directly as:
where is the long difference in the variable of interest from the end of quarter t to t + h, that is is the quarterly difference in yt and Xt is a vector of additional macroeconomic controls.[29] In contrast to the identifying assumption of the SVAR, the LP framework allows for an immediate effect of a monetary policy shock on the dependent variable.[30] The parameter provides the estimate for the change in the variable of interest between end of quarter t and t + h attributed to the monetary policy shock occurring during quarter t + 1.
Overall, the results from the regressions are very similar to the SVAR results (Figure D2). In particular, I find no evidence of a price puzzle when using the new preferred, unanticipated BT-CS shock. However, the unemployment response is smaller and appears to be negative in the long run.
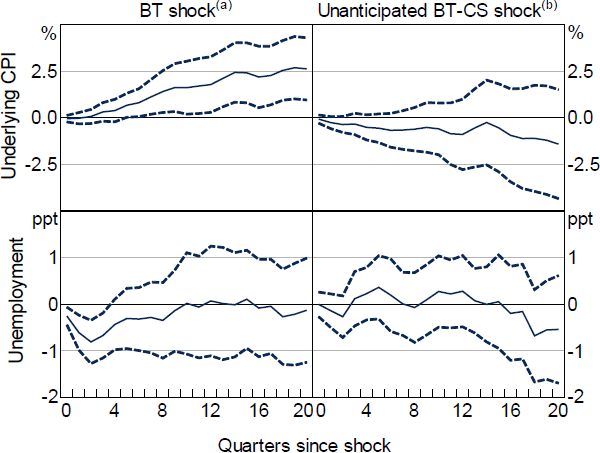
Notes:
Dashed lines show 90% heteroskedasticity and autocorrelation robust confidence intervals
(a) Original, anticipated policy sock used by Bishop and Tulip (2017)
(b) New, preferred unanticipated policy shock
D.2 Different Cash Rate Reaction Function
To allow comparison between the estimates, I followed the Bishop and Tulip (2017) specification for the RR regression which includes the lagged level of the cash rate and the nowcast of the unemployment rate. One possibility is that the inclusion of credit spreads just captures other variables to which the Bank responds when setting the cash rate and that the baseline Taylor rule is hence misspecified. Accordingly, I find that two changes to this benchmark specification increase the fit of the model considerably even before adding any money and credit market spreads. Specifically, I replace the lagged level of the cash rate with the previous change in the cash rate and the nowcast of the unemployment rate with the two-quarter-ahead forecast. Both coefficients are statistically significant and increase the model fit from around 25 to 40 per cent (Table D1, regression BT). Furthermore, I find a small but significant response of the cash rate to variables capturing international conditions, in particular commodity price inflation , albeit with an unexpected, negative sign) and the nominal trade-weighted exchange rate . This may suggest that the cash rate in part responds to the global (financial) cycle.
| Variable | BT | BT-CS1 | BT-CS2 | BT-CS3 | BT-CS | BT-Int | BT-CS-Int |
|---|---|---|---|---|---|---|---|
| Constant | −0.18 | 0.06 | −0.01 | −0.05 | 0.27** | −0.16 | 0.22* |
| 0.35*** | 0.20** | 0.33*** | 0.31*** | 0.17* | 0.24** | 0.12 | |
| 0.07** | 0.03 | 0.08** | 0.08** | 0.04 | 0.07** | 0.03 | |
| 0.01 | −0.01 | 0.01 | 0.00 | −0.01 | 0.01 | −0.01 | |
| −0.32*** | −0.20** | −0.34*** | −0.25** | −0.19** | −0.36*** | −0.28*** | |
| 0.21*** | 0.20*** | 0.16** | 0.21*** | 0.15** | 0.23*** | 0.18*** | |
| 0.11*** | 0.08*** | 0.13*** | 0.11*** | 0.10*** | 0.09*** | 0.09*** | |
| −0.56*** | −0.52*** | −0.48*** | |||||
| −0.08*** | −0.08*** | −0.09*** | |||||
| −0.05 | −0.03 | 0.01 | |||||
| 0.01 | 0.02* | ||||||
| ntwit | 0.02*** | 0.01*** | |||||
| 0.00 | −0.00 | ||||||
| Observations | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| R 2 | 0.430 | 0.561 | 0.480 | 0.445 | 0.607 | 0.536 | 0.692 |
| Adjusted R 2 | 0.393 | 0.527*** | 0.440*** | 0.403 | 0.568*** | 0.490 | 0.650*** |
| Notes: Statistical significance of the difference in model fit (Adjusted R 2) to the benchmark (excluding credit spreads or international variables) is assessed using a likelihood ratio test; see Table 1 for further notes | |||||||
Nonetheless, credit market spreads still add significant explanatory value for cash rate changes to these alternative baseline specifications. Similarly, these changes to the BT regression have no material impact on the estimated impulse responses (Figure D3). The price puzzle disappears only when controlling for the response of the cash rate to credit market conditions and taking into account the anticipation of cash rate changes by financial market participants. When including international conditions to the alternative RR regressions, the effects of a cash rate change are slightly more contractionary for both inflation and the unemployment rate.
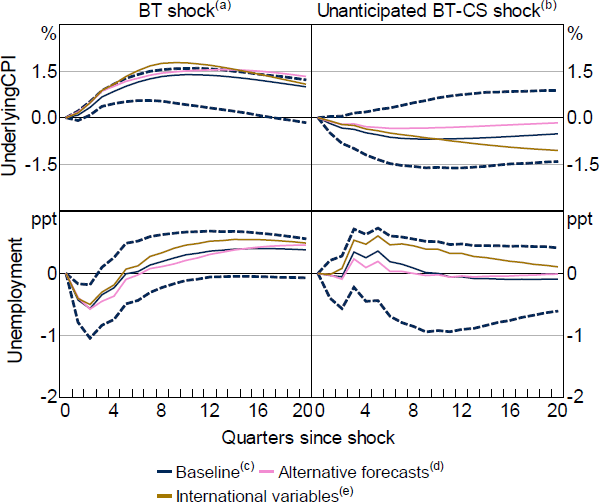
Notes:
Impulse responses to policy shocks obtained from alternative baseline Taylor rule regression (Table D1), see Figures 7 and 9 for further notes
(a) Original, anticipated policy shock used by Bishop and Tulip (2017)
(b) New, preferred unanticipated policy shock
(c) Original Taylor rule specification used by Bishop and Tulip (2017)
(d) Alternative Taylor rule specification (regression BT-CS of Table D1)
(e) Alternative Taylor rule specification including international conditions (regression BT-CS-Int of Table D1)
D.3 Further Results
Credit market conditions and inflation forecast errors across all horizons
| Predictor | Horizon (in quarters) | |||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 6 | 8 | |||||
| Constant | −0.11 | −0.06 | −0.38* | −0.10 | −0.03 | 1.37* | 1.08* | 2.97** |
| −1.41*** | −1.44*** | −1.15*** | −1.24*** | 1.17*** | 0.88** | 1.75** | 1.48 | |
| 0.04 | 0.03 | 0.02 | 0.04 | −0.15 | 0.09 | −0.35 | −0.05 | |
| 0.06 | 0.07* | 0.10 | 0.10 | 0.31* | 0.31** | 0.45* | 0.39* | |
| 0.10 | −0.32* | −0.80* | −0.51 | |||||
| −0.03 | −0.10 | −0.43* | −0.63 | |||||
| Observations | 96 | 96 | 95 | 95 | 87 | 87 | 78 | 78 |
| R 2 | 0.784 | 0.786 | 0.391 | 0.417 | 0.375 | 0.370*** | 0.234 | 0.311** |
| F-statistic | 45.75*** | 35.05*** | 7.99*** | 6.74*** | 3.94*** | 5.12*** | 3.05*** | 3.41*** |
| Note: See Table 4 for notes | ||||||||
Estimated effects of monetary policy: the role of individual credit spreads measures
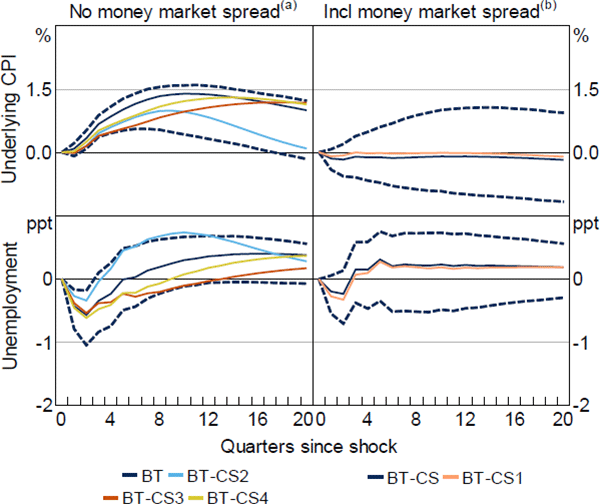
Notes:
Impulse responses from the benchmark recursive SVAR with one of the policy shocks from Table 1, see Figure 7 for further notes
(a) Bishop and Tulip ((2017), updated, BT) policy shock with confidence intervals, or BT shock accounting for cash rate response to domestic lending rate spread (BT-CS2), US corporate bond spread (BT-CS3) or US VIX (BT-CS4)
(b) BT shock accounting for cash rate response to all credit spread measures (BT-CS) with confidence intervals, or BT shock accounting for cash rate response to domestic money market spread (BT-CS1)
References
Adrian T and F Duarte (2016), ‘Financial Vulnerability and Monetary Policy’, Federal Reserve Bank of New York Staff Report No 804, rev September 2017.
Ballantyne A, T Cusbert, R Evans, R Guttmann, J Hambur, A Hamilton, E Kendall, R McCririck, G Nodari and D Rees (2019), ‘MARTIN Has Its Place: A Macroeconometric Model of the Australian Economy’, RBA Research Discussion Paper No 2019-07.
Barakchian SM and C Crowe (2013), ‘Monetary Policy Matters: Evidence from New Shocks Data’, Journal of Monetary Economics, 60(8), pp 950–966.
Bassett WF, MB Chosak, JC Driscoll and E Zakrajšek (2014), ‘Changes in Bank Lending Standards and the Macroeconomy’, Journal of Monetary Economics, 62, pp 23–40.
Beechey M and P Österholm (2008), ‘A Bayesian Vector Autoregressive Model with Informative Steady-State Priors for the Australian Economy’, The Economic Record, 84(267), pp 449–465.
Berkelmans L (2005), ‘Credit and Monetary Policy: An Australian SVAR’, RBA Research Discussion Paper No 2005-06.
Bernanke BS, J Boivin and P Eliasz (2005), ‘Measuring the Effects of Monetary Policy: A Factor-Augmented Vector Autoregressive (FAVAR) Approach’, The Quarterly Journal of Economics, 120(1), pp 387–422.
Bernanke BS and M Gertler (1989), ‘Agency Costs, Net Worth, and Business Fluctuations’, The American Economic Review, 79(1), pp 14–31.
Bernanke BS, M Gertler and S Gilchrist (1999), ‘The Financial Accelerator in a Quantitative Business Cycle Framework’, in JB Taylor and M Woodford (eds), Handbook of Macroeconomics: Volume 1C, Handbooks in Economics 15, Elsevier Science, Amsterdam, pp 1341–1393.
Bishop J and P Tulip (2017), ‘Anticipatory Monetary Policy and the “Price Puzzle”’, RBA Research Discussion Paper No 2017-02.
Brischetto A and G Voss (1999), ‘A Structural Vector Autoregression Model of Monetary Policy in Australia’, RBA Research Discussion Paper No 1999-11.
Caggiano G, E Castelnuovo and G Nodari (2018), ‘Risk Management-Driven Policy Rate Gap’, Economic Letters, 171, pp 235–238.
Caldara D and E Herbst (2019), ‘Monetary Policy, Real Activity, and Credit Spreads: Evidence from Bayesian Proxy SVARs’, American Economic Journal: Macroeconomics, 11(1), pp 157–192.
Cochrane JH and M Piazzesi (2002), ‘The Fed and Interest Rates—A High-Frequency Identification’, The American Economic Review, 92(2), pp 90–95.
Coibion O (2012), ‘Are the Effects of Monetary Policy Shocks Big or Small?’, American Economic Journal: Macroeconomics, 4(2), pp 1–32.
Debelle G (2018), ‘Lessons and Questions from the GFC’, Address to the Australian Business Economists Annual Dinner, Sydney, 6 December.
Dungey M and A Pagan (2000), ‘A Structural VAR Model of the Australian Economy’, Economic Record, 76(235), pp 321–342.
Eickmeier S and T Ng (2015), ‘How Do US Credit Supply Shocks Propagate Internationally? A GVAR Approach’, European Economic Review, 74, pp 128–145.
Evans C, J Fisher, F Gourio and S Krane (2015), ‘Risk Management for Monetary Policy Near the Zero Lower Bound’, Brookings Papers on Economic Activity, Spring, pp 141–196.
Finlay R and J Jääskelä (2014), ‘Credit Supply Shocks and the Global Financial Crisis in Three Small Open Economies’, Journal of Macroeconomics, 40, pp 270–276.
Finlay R and D Olivan (2012), ‘Extracting Information from Financial Market Instruments’, RBA Bulletin, March, pp 45–54.
Florio A (2018), ‘Nominal Anchors and the Price Puzzle’, Journal of Macroeconomics, 58, pp 224–237.
Gambetti L and A Musso (2017), ‘Loan Supply Shocks and the Business Cycle’, Journal of Applied Econometrics, 32(4), pp 764–782.
Gertler M and P Karadi (2015), ‘Monetary Policy Surprises, Credit Costs, and Economic Activity’, American Economic Journal: Macroeconomics, 7(1), pp 44–76.
Gilchrist S and E Zakrajšek (2012), ‘Credit Spreads and Business Cycle Fluctuations’, The American Economic Review, 102(4), pp 1692–1720.
Gürkaynak RS, B Sack and E Swanson (2005), ‘The Sensitivity of Long-Term Interest Rates to Economic News: Evidence and Implications for Macroeconomic Models’, The American Economic Review, 95(1), pp 425–436.
Hanson MS (2004), ‘The “Price Puzzle” Reconsidered’, Journal of Monetary Economics, 51(7), pp 1385–1413.
Hartigan L and J Morley (2018), ‘A Factor Model Analysis of the Effects of Inflation Targeting on the Australian Economy’, in J Simon and M Sutton (eds), Central Bank Frameworks: Evolution or Revolution?, Proceedings of a Conference, Reserve Bank of Australia, Sydney, pp 127–160.
Jääskelä J and D Jennings (2010), ‘Monetary Policy and the Exchange Rate: Evaluation of VAR Models’, RBA Research Discussion Paper No 2010-07.
Jacobs D and V Rayner (2012), ‘The Role of Credit Supply in the Australian Economy’, RBA Research Discussion Paper No 2012-02.
Jordà Ò (2005), ‘Estimation and Inference of Impulse Responses by Local Projections’, The American Economic Review, 95(1), pp 161–182.
Kim S and K Lim (2018), ‘Effects of Monetary Policy Shocks on Exchange Rate in Small Open Economies’, Journal of Macroeconomics, 56, pp 324–339.
Kiyotaki N and J Moore (1997), ‘Credit Cycles’, Journal of Political Economy, 105(2), pp 211–248.
Kuttner KN (2001), ‘Monetary Policy Surprises and Interest Rates: Evidence from the Fed Funds Futures Market’, Journal of Monetary Economics, 47(3), pp 523–544.
Lawson J and D Rees (2008), ‘A Sectoral Model of the Australian Economy’, RBA Research Discussion Paper No 2008-01.
Leeper EM, TB Walker and S-CS Yang (2013), ‘Fiscal Foresight and Information Flows’, Econometrica, 81(3), pp 1115–1145.
López-Salido D, JC Stein and E Zakrajšek (2017), ‘Credit-Market Sentiment and the Business Cycle’, The Quarterly Journal of Economics, 132(3), pp 1373–1426.
Mertens K and MO Ravn (2013), ‘The Dynamic Effects of Personal and Corporate Income Tax Changes in the United States’, The American Economic Review, 103(4), pp 1212–1247.
Miranda-Agrippino S and G Ricco (2018), ‘The Transmission of Monetary Policy Shocks’, Centre for Economic Policy Research Discussion Paper DP13396.
Phan T (2014), ‘Output Composition of the Monetary Policy Transmission Mechanism: Is Australia Different?’, Economic Record, 90(290), pp 382–399.
Plagborg-Møller M and CK Wolf (2019), ‘Local Projections and VARs Estimate the Same Impulse Responses’, Unpublished manuscript, Princeton University, 3 November.
Ramey VA (2016), ‘Macroeconomic Shocks and Their Propagation’, in JB Taylor and H Uhlig (eds), Handbook of Macroeconomics: Volume 2A, Handbooks in Economics, Elsevier, Amsterdam, pp 71–162.
RBA (Reserve Bank of Australia) (2008a), ‘Minutes of the Monetary Policy Meeting of the Reserve Bank Board, Melbourne – 2 December 2008’.
RBA (2008b), ‘Minutes of the Monetary Policy Meeting of the Reserve Bank Board, Sydney – 4 November 2008’.
RBA (2008c), ‘Minutes of the Monetary Policy Meeting of the Reserve Bank Board, Sydney – 7 October 2008’.
RBA (2008d), Statement on Monetary Policy, November.
RBA (2009), Statement on Monetary Policy, February.
Rey H (2015), ‘Dilemma not Trilemma: The Global Financial Cycle and Monetary Policy Independence’, NBER Working Paper No 21162, rev February 2018.
Romer CD and DH Romer (2004), ‘A New Measure of Monetary Shocks: Derivation and Implications’, The American Economic Review, 94(4), pp 1055–1084.
Rusnak M, T Havranek and R Horvath (2013), ‘How to Solve the Price Puzzle? A Meta-Analysis’, Journal of Money, Credit and Banking, 45(1), pp 37–70.
Sharpe SA, NR Sinha and CA Hollrah (2017), ‘What's the Story? A New Perspective on the Value of Economic Forecasts’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2017-107.
Sims CA (1992), ‘Interpreting the Macroeconomic Time Series Facts: The Effects of Monetary Policy’, European Economic Review, 36(5), pp 975–1000.
Stock JH and MW Watson (2018), ‘Identification and Estimation of Dynamic Causal Effects in Macroeconomics Using External Instruments’, The Economic Journal, 128(610), pp 917–948.
Suzuki T (2004), ‘Is the Lending Channel of Monetary Policy Dominant in Australia?’, Economic Record, 80(249), pp 145–156.
Tulip P and S Wallace (2012), ‘Estimates of Uncertainty around the RBA's Forecasts’, RBA Research Discussion Paper No 2012-07.
Acknowledgements
The Discussion Paper series is intended to make the results of the current economic research within the Reserve Bank available to other economists. Its aim is to present preliminary results of research so as to encourage discussion and comment. Views expressed in this paper are those of the authors and not necessarily those of the Reserve Bank. Use of any results from this paper should clearly attribute the work to the authors and not to the Reserve Bank of Australia.
Footnotes
Rusnak, Havranek and Horvath (2013) find that half of 70 studies using structural vector autoregressions (SVARs) exhibit the price puzzle. But even for seminal studies that are free of the price puzzle, Ramey (2016) finds that many are not robust to small modifications to specification choices or identifying assumptions. For Australia, only one-third of the studies using SVARs find no price puzzle (see Appendix A). [1]
In other words, the identified policy ‘shock’ cannot be the true monetary policy shock as it is contemporaneously correlated with a financial market shock. In the related literature identifying the effects of macroeconomic shocks using external instruments this represents a violation of the exogeneity condition (Mertens and Ravn 2013; Gertler and Karadi 2015; Stock and Watson 2018). [2]
This relates to the issue of non-fundamentalness in SVARs when policy shocks are anticipated or announced prior to implementation, such as in the case of forward guidance (Leeper, Walker and Yang 2013; Ramey 2016). [3]
It should be noted that my estimates suggest smaller cash rate effects than recent estimates from a factor augmented VAR model by Hartigan and Morley (2018). Providing external validity to models like MARTIN is important since the dynamic properties of MARTIN (or any large-scale macroeconometric model) may be sensitive to misspecification of only a few of the model's many equations. Such misspecifications can, for example, arise from the fact that MARTIN relies partly on calibrated relationships between some variables to ensure satisfactory long-run properties of the model. [4]
This is not to say that the role of financial markets for the real economy was ignored prior to the GFC. Examples include Bernanke and Gertler (1989), Bernanke, Gertler and Gilchrist (1999) and Kiyotaki and Moore (1997), who emphasise the role of household and firm balance sheets as amplifiers of business cycles. But since the GFC, this literature has grown rapidly to show that shocks originating in credit markets can have considerable effects on the real economy (see Gilchrist and Zakrajšek (2012), Bassett et al (2014), Gambetti and Musso (2017) and López-Salido, Stein and Zakrajšek (2017) for international evidence; and Jacobs and Rayner (2012) and Finlay and Jääskelä (2014) for Australia). [5]
The additional response of monetary policy to financial conditions suggested by Adrian and Duarte (2016) is, however, motivated by the predictive value of credit market indicators for future output over and above past realisations of all other variables. If the central bank's forecasts were to fully centralise this information, responding to these forecasts should deliver the same policy decision. [6]
See Appendix B for further derivations of the estimators. [7]
Another source of bias may be that the cash rate affects inflation through Zt, that is, . Gilchrist and Zakrajšek (2012) and Caldara and Herbst (2019) show that credit market conditions are an important transmission channel for monetary policy. Modelling this channel explicitly does not change my results as shown Section 6.1. [8]
One approach to condense the information of a broad range of indicators is to estimate ‘factors’ that capture common signals from the set of indicators and add these factors to the VAR model (Bernanke, Boivin and Eliasz 2005). Hartigan and Morley (2018) find that this resolves the price puzzle for Australia. However, the factor model assumes that the Bank's forecasts are obtained by linearly combining all observable information. Furthermore, the factor model cannot observe ‘soft’ information (e.g. information obtained through liaison) and additional staff judgement. [9]
I will use the term ‘shock’ going forward. However, the purged cash rate change may be endogenous to other (short-term) objectives of the Bank. Thus, it may be better thought of as an ‘instrument’ for the part of a cash rate change that is exogenous with regard to the central bank's inflation and growth outlooks rather than a ‘structural disturbance’ in a fully specified model (Ramey 2016). The obtained policy shocks do not have to be, and are not necessarily, exogenous to the Bank's outlook for other variables. [10]
An alternative explanation could be that the Bank's staff anticipated the strong cash rate response to offset any effects of the GFC on inflation and unemployment even in the short to medium term. This is unlikely given the typically assumed long lags with which a cash rate change would affect real economic activity and inflation. [12]
All subsequent results are robust to changes to this specification as discussed in Appendix D. [13]
The Bank arguably targets inflation at much longer horizons than two quarters. But the Bank's longer-term forecasts for inflation and economic activity are conditional on an assumed or predicted path of the cash rate and hence include feedback effects from the policy decision. This motivates the use of forecasts for short horizons. At these horizons, any immediate cash rate changes are unlikely to have material effects on inflation and economic activity. At the same time, inflation and output are strongly serially correlated, so that short-term forecasts should provide a good approximation of longer-term forecasts (Romer and Romer 2004). [14]
The Reserve Bank Board meets on the first Tuesday of every month except January (11 times per year) to set the cash rate. For four of these meetings, the Bank staff updates all forecasts. I only use cash rate changes for these forecast months (end-quarter months prior to 2000 and mid-quarter months since) to estimate the policy reaction function (Equation (15)). BT show that using cash rate changes for all meetings and using internal staff forecasts or forecasts from Consensus Economics does not resolve the price puzzle. The forecasts used are updated from BT and are forecasts as published in the SMP a few days after the Board meeting. BT show that changes to the forecasts after the meeting are usually trivially small, and do not correlate with either cash rate increases or decreases. [15]
Using these indicators, the literature has explored the role of credit supply shocks originating from shifts in risk sentiment of investors for the business cycle (e.g. López-Salido et al 2017), and found these indicators have strong predictive power for future economic activity (e.g. Gilchrist and Zakrajšek 2012). [16]
I further explored spreads between small and large business lending rates, and the variable mortgage to cash rate spread but found no response of the cash rate to these spreads over and above the Bank's forecasts and the other spread measures. [17]
I obtain these expectations from the zero-coupon yield curve estimated by Finlay and Olivan (2012). I use the cash rate change as expected on the last day of the month preceding the Board meeting to align this measure with the credit spread measures. [18]
It may also suggest that policy changes are communicated in advance. While the Bank occasionally communicates its outlook on the likely direction of future cash rate changes, it does not publish a forecast for the cash rate path nor has it engaged in direct forward guidance. This explanation is hence less likely to explain this finding. [19]
In contrast to Ramey (2016) and Miranda-Agrippino and Ricco (2018) I find no evidence for serial autocorrelation in any of the shock series. [20]
I account for lags in data availability for inflation, unemployment and real GDP but not for revisions. Instead, I use final revised data as available in 2019:Q1 in both Zt –1 and when computing the forecast error. [21]
The results are also robust to including the expected cash rate change as a predictor for inflation forecasts. [22]
I find that the US VIX has considerable predictive content for unemployment forecast errors. However, the cash rate does not appear to respond to the US VIX over and above domestic credit spreads, and hence this additional predictive content should not introduce any systematic bias to the estimated unemployment response to cash rate changes. [23]
The positive association between lending spreads and economic activity could reflect increased credit demand to finance investment. Later, as investment comes on line, the productive capacity and aggregate supply increase which may lower prices. However, investment may also lift labour productivity and thereby wages, aggregate demand and inflation. [24]
As the policy shocks should already be exogenous to other variables in the VAR, an alternative would be to order the policy shock first and allow all other variables to respond to the shock instantaneously. My results are robust to this and other SVAR specifications, as well as using the local projection (LP) framework by Jordà (2005) to estimate impulse responses (Appendix D). This suggests that the price puzzle does not emerge due to a misspecification of the reduced-form VAR dynamics. [25]
Since the cash rate responds most strongly to domestic money market conditions (Table 1), I find that taking this response into account matters most for resolving the price puzzle. The responses to other financial conditions alone do not resolve the price puzzle; see Figure D4. [26]
Miranda-Agrippino and Ricco go the opposite direction and purge financial market surprises around Fed monetary policy announcement dates of the Fed's Greenbook forecasts. [27]
This framework allows estimating the effects of monetary policy without imposing the heavy parametric structure of the SVAR. Plagborg-Møller and Wolf (2019) show that this approach is conceptually identical to the SVAR approach and estimates the same impulse responses. However, and analogous to the choice between ‘direct’ and ‘iterated’ multi-horizon forecasting, VAR impulse responses (iterated) are more efficient if the chosen VAR accurately describes the data-generating process, whilst LP impulse responses (direct) are more robust to model misspecification. [28]
I include quarterly inflation, the quarterly growth rate of real GDP, and the change in the unemployment rate unless already included in the autoregressive term . I set P = Q = 4 and R = 1. Adding controls and lagged monetary policy shocks may provide more precisely estimated effects and soak up any residual autocorrelation in the shocks. [29]
I include all macroeconomic controls with a lag. Including simultaneous realisations of Xt may bias the coefficient of interest if the monetary policy shock affects these controls contemporaneously. As such, LP regressions including contemporaneous realisations of the controls impose the same timing assumptions as the standard, Cholesky-identified SVAR. Ramey (2016) finds that these timing assumptions are not innocuous. [30]