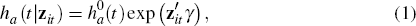RDP 2014-13: Mortgage-related Financial Difficulties: Evidence from Australian Micro-level Data 2. Loan-level Determinants of Housing Loan Arrears
November 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 728KB
In this section, we use data on individual residential mortgages to explore the factors associated with entering 90+ day housing loan arrears. Borrowers in arrears by 90+ days are behind on their payments by at least three monthly contractual payments. We focus on loans that are at least 90 days in arrears, as these should correspond to borrowers that are experiencing serious financial difficulties rather than short-term liquidity problems. Additionally, arrears of this duration are consistent with the definition of default in the Basel II regulations.
2.1 Data
The loan-level dataset used in this paper is provided by MARQ Services (a firm that provides investors with information on the collateral pools backing residential mortgage-backed securities (RMBS)).[3] It contains monthly observations on housing loans that were originated between 1994 and 2013 and were securitised by two non-major banks. During the sample period from late 2009 to early 2014, the loan pool contained around 72,000 loans, with an average of around 25 monthly observations per loan.[4] Around 1,300 of these loans (1.8 per cent) were in arrears by more than 90 days at some point in the sample.
To investigate the representativeness of the sample, we compare its composition against that of broader samples at a particular point in time. Table 1 compares the sample against on-balance sheet and securitised housing loans. In the first case this information comes from APRA, while in the second case it is from Perpetual (the trustee for the majority of RMBS in Australia). Table 2 presents further selected descriptive statistics for the MARQ sample.
| Characteristic | Data source | ||
|---|---|---|---|
| MARQ | APRA | Perpetual | |
| 90+ day arrears rate | 0.6 | 0.7 | 0.5 |
| Fixed rate | 7.5 | 12.6 | 11.0 |
| Interest only | 23.2 | 32.7 | 21.5 |
| Investor | 26.0 | 32.9 | 26.9 |
| Low doc | 8.3 | 5.4 | 6.2 |
| Loan purpose | |||
| Home improvement | 3.5 | na | 1.9 |
| Property purchase | 49.6 | na | 53.7 |
| Refinance | 36.3 | na | 24.4 |
| Other | 10.6 | na | 20.0 |
| State | |||
| NSW | 32.8 | na | 31.6 |
| QLD | 39.7 | na | 23.7 |
| VIC | 15.1 | na | 23.3 |
|
Notes: Institutional coverage differs across data sources and across loan characteristics within data sources; in the APRA data, loans that are 90+ days in arrears include impaired loans that are not past due; ‘other’ includes construction, home equity loans and loans where the purpose is unknown Sources: APRA; Authors' calculations; MARQ Services; Perpetual |
|||
| Characteristic | Percentiles | Mean | ||
|---|---|---|---|---|
| 25th | 50th | 75th | ||
| LVR at origination (%) | 47.4 | 69.7 | 80.0 | 64.1 |
| Interest rate (%) | 6.8 | 7.0 | 7.3 | 7.1 |
| Local unemployment rate (%) | 4.0 | 5.1 | 5.9 | 5.0 |
| Required payment ($'000) | 0.7 | 1.3 | 1.9 | 1.4 |
| Loan age (years) | 4.8 | 6.0 | 7.6 | 6.6 |
|
Note: ‘Local unemployment rate’ is the unemployment rate in the Statistical Area Level 4 (SA4) region in which the mortgaged property is located (there are around 90 SA4 regions in Australia and the median number of postcodes per region is around 30) Sources: ABS; Authors' calculations; MARQ Services |
||||
As at December 2011, the sample contained 43,800 loans worth around $8.5 billion (equivalent to about 0.7 per cent of housing credit). The sample appears broadly similar in composition to the Perpetual loan pool across a number of loan characteristics. Notably, the 90+ day arrears rate for the sample is similar to arrears rates calculated using the other two data sources. While there are some differences in composition between the sample and the broader loan pools, this does not necessarily imply that the results from our analysis will be biased. We are interested in the relationship between certain variables and housing loan arrears. As long as the performance of the loans in this sample responded to these variables in the same way as loans in the broader loan pool, then our results will generalise to the population of housing loans.
Table 3 presents 90+ day arrears rates in the sample across a range of loan characteristics. Broadly speaking, the patterns in these arrears rates are consistent with aggregate data sources. For example: the arrears rate on low-doc loans is much higher than on full-doc loans; the arrears rates on investor and owner-occupier loans are broadly similar; the arrears rate on fixed-rate loans is lower than on variable-rate loans; and the arrears rate tends to increase with the LVR at origination.[5] Overall, however, we suggest caution in making inferences about the broader population of housing loans based on this sample; the sample contains loans from a small subset of lenders and lending practices may differ across lenders.
| LVR at origination | Loan documentation | ||
| 0 ≤ LVR < 60 | 0.18 | Full doc | 0.33 |
| 60 ≤ LVR < 80 | 0.52 | Low doc | 1.70 |
| 80 ≤ LVR < 90 | 0.59 | Loan purpose | |
| 90 ≤ LVR < 100 | 0.72 | Home improvement | 0.21 |
| LVR ≥ 100 | 0.51 | Property purchase | 0.35 |
| Employment type | Refinance | 0.51 | |
| Self-employed | 1.13 | Other | 0.44 |
| Wage earner | 0.32 | Property purpose | |
| Interest rate type | Investor | 0.49 | |
| Fixed | 0.12 | Owner-occupier | 0.42 |
| Variable | 0.46 | Payment type | |
| Amortising | 0.43 | ||
| Interest only | 0.44 | ||
|
Note: Arrears rates calculated over entire sample (October 2009 to January 2014) Sources: Authors' calculations; MARQ Services |
|||
One potentially important variable that is not available in the dataset is the minimum required mortgage payment. For amortising loans, we estimate this using a credit-foncier model, which assumes that borrowers make constant payments over the life of the loan so that the loan principal is paid down to zero at loan maturity (based on the prevailing interest rate). For interest-only loans, the required payment is estimated as the product of the remaining loan balance and the interest rate.
The valuation for the mortgaged property available in the dataset is the value at loan origination and is not updated over time. We use hedonically adjusted price series to estimate dwelling price growth. For Sydney, Melbourne and Brisbane we use postcode-level indices we have estimated from unit-record data provided by Australian Property Monitors (APM) (see Appendix B for details on construction of the hedonic dwelling price indices). For all other areas, we use capital city or rest-of-state hedonic indices provided by RP Data-Rismark, as postcode-level dwelling price data were not available outside Sydney, Melbourne and Brisbane. While both types of indices are only estimates, they should be a reasonable proxy for borrowers' beliefs about property values to the extent that borrowers adjust their beliefs based on observing sales prices of nearby properties. Gerardi et al (2013) argue that perceived valuations are more relevant to mortgage default decisions than actual values, as households take into account their own valuation of their property when choosing whether to default.
2.2 Modelling Framework
Duration analysis provides a framework for modelling ‘time-to-event’ data. In our case, the time-to-event is the time between loan origination and a loan falling into arrears. Importantly, duration models can provide estimates of the effects of covariates on the probability of entering arrears. The advantages of using duration analysis to model housing loan arrears are that it accounts for ‘right-censoring’ (where the ultimate outcome of the loan is not observed) and can parsimoniously account for time dependence (where the probability of entering arrears is a function of the time since loan origination).
Duration analysis of arrears data is complicated by the fact that most housing loans are paid down in full before or when the loan matures. Application of standard duration analysis techniques is inappropriate in the presence of ‘competing risks’ – that is, events that prevent observational units from ever experiencing the event of interest. In this case, the competing risk is the loan being paid down in full. Standard duration analysis techniques would treat loans that have been paid down in full as being censored. They would also assume that these loans could still fall into arrears, which is clearly inappropriate, as a loan that has been paid down no longer exists and thus has zero probability of entering arrears. In cases where the probability of experiencing the competing risk is correlated with the covariates of interest, standard duration analysis techniques can yield misleading estimates of the effects of these covariates on the probability that the event of interest occurs.
Competing risks regression models provide a framework for analysing time-to-event data in the presence of competing risks. Competing risks frameworks have previously been used to model default for housing, commercial and personal loans. For example, for the United States, Deng, Quigley and Van Order (2000) estimate a competing risks model for residential mortgage default and prepayment, while Ciochetti et al (2002) estimate a similar model for commercial mortgages. Watkins, Vasnev and Gerlach (2014) estimate a competing risks model using data on personal loans made by an Australian bank.
In standard duration analysis, the hazard function, h(t), approximates the instantaneous probability of an event occurring at time t conditional on it having not occurred before time t.[6] In a competing risks framework, Fine and Gray (1999) propose a model for the hazard function of the subdistribution of the event of interest, which they call the ‘subhazard’ (for technical details, see Appendix C). When incorporating covariates, the model for the subhazard of entering arrears (denoted by the subscript a) takes a proportional hazards form:
where zit is a vector of explanatory variables
corresponding to loan i, γ is a vector of coefficients and 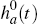 is the baseline subhazard, which accounts for time dependence (outside of the effects
of time-varying covariates). The model is semi-parametric, since the shape
of the baseline subhazard is left unspecified.
is the baseline subhazard, which accounts for time dependence (outside of the effects
of time-varying covariates). The model is semi-parametric, since the shape
of the baseline subhazard is left unspecified.
The estimation results reported in Section 2.3 are exponentiated coefficients (i.e. exp(γk) for variable k), which are known as ‘subhazard ratios’ (SHRs). An SHR of exp(γk) means that a one unit increase in variable k results in the subhazard being exp(γk) times its original value. Therefore, an SHR greater than one implies that an increase in the covariate results in the subhazard increasing. The significance levels reported in Section 2.3 correspond to the null hypothesis that the coefficient on that variable is equal to zero, which is equivalent to an SHR of one.
We estimate a competing risks regression model for mortgage arrears, where the competing risk is full payment (either before or at loan maturity). A loan is classified as having been paid down in full if it drops out of the loan pool before the latest report date. Loans that are outstanding on the latest report date but are not in arrears are considered right-censored. A loan is classified as being in arrears if it is in arrears by more than 90 days. Once a loan has entered arrears, it is removed from the set of loans ‘at risk’ of entering arrears – that is, we do not allow loans that are in arrears to ‘cure’ (i.e. return to performing status without refinancing).
Of loans that entered 90+ day arrears in December 2011, around 40 per cent of these loans had returned to performing status three months later, while around 45 per cent remained in 90+ day arrears.[7] The remaining loans had exited from the loan sample, probably because the borrower paid the loan down by selling the property or they refinanced (although a very small number of borrowers may have had their property repossessed). Given the relatively small sample of loans that cure, it is unlikely that our sample would provide much information on the factors associated with curing. However, this could be an interesting avenue for further research when more loan-level data become available, because curing rates will affect the stock of loans that are in arrears at a given time.
2.3 Results
Table 4 presents results for a competing risks regression model for mortgage arrears.[8] As explanatory variables, the model includes the LVR at origination (as a sequence of dummy variables to capture potential nonlinearities), the percentage of the loan balance that has been paid down since origination (i.e. amortisation), the cumulative percentage growth of dwelling prices since origination, the local unemployment rate, the current mortgage interest rate for each loan and a number of other loan characteristics.
| Explanatory variable | SHR | Explanatory variable | SHR |
|---|---|---|---|
| Amortisation | 0.99*** | Investor | 0.91 |
| LVR at origination | Loan purpose | ||
| 60 ≤ LVR< 80 | 1.75*** | Home improvement | 0.47** |
| 80 ≤ LVR< 90 | 1.93*** | Refinance | 1.77*** |
| 90 ≤ LVR< 100 | 3.47*** | Other | 1.16 |
| LVR ≥ 100 | 2.77*** | Local unemployment rate | 1.03* |
| Dwelling price growth | 1.00 | Low doc | 1.76*** |
| Fixed rate | 0.39*** | Minimum required payment | 1.31*** |
| Interest only | 0.56*** | Self-employed | 1.19 |
| Interest rate | 1.35*** | ||
| Number of observations | 1,612,645 | ||
| Number of loans | 63,468 | ||
| Number entered arrears | 1,056 | ||
| Number paid in full | 25,841 | ||
| Number censored | 36,571 | ||
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively; standard errors are clustered by loan; ‘amortisation’ is the percentage decrease in the loan balance since origination; ‘dwelling price growth’ is the cumulative percentage growth of dwelling prices since origination; ‘minimum required payment’ is measured in thousands of dollars Sources: ABS; APM; Authors' calculations; MARQ Services; RP Data-Rismark |
|||
2.3.1 Equity factors
The model provides evidence to suggest that equity factors are associated with the probability of falling into arrears; both the LVR at origination and the amount of amortisation since origination have statistically (and economically) significant SHRs. The subhazard of entering arrears tends to increase with the LVR at origination. For example, a loan with an LVR at origination of between 90 and 100 per cent has an estimated subhazard of entering arrears that is about 3½ times that of a loan with an LVR less than 60 per cent (to put these results into perspective, in Section 2.3.4 we select a ‘base’ loan and examine how the probability of entering arrears before a certain loan age varies with loan characteristics). Additionally, the subhazard of entering arrears appears to increase nonlinearly, and is particularly high for loans with an LVR between 90 and 100 per cent; a loan with an LVR at origination of between 80 and 90 per cent has a subhazard of entering arrears that is about 1.1 times higher than that of a loan with an LVR between 60 and 80 per cent, but a loan with an LVR of between 90 and 100 per cent has a subhazard of entering arrears that is almost twice that of a loan with an LVR between 80 and 90 per cent.
Somewhat counterintuitively, the results suggest that loans with an LVR at origination greater than 100 per cent are less likely to fall into arrears than loans with an LVR between 90 and 100 per cent. However, as mentioned previously, this is likely to reflect measurement error; the dataset contains information on only the first property securing each loan, implying that loans with multiple properties as security will have an LVR at origination that is overestimated (because the value of the collateral is underestimated).
The amortisation variable has an estimated SHR that is statistically smaller than one, indicating that an increase in cumulative amortisation is associated with a decrease in the subhazard of entering arrears. The magnitude of the effect appears fairly small, at 0.99. However, the effect of an x percentage point increase in cumulative amortisation will be associated with a subhazard that is about 0.99x times lower. For example, a 10 percentage point increase in cumulative amortisation is associated with a subhazard that is around 0.9 times lower, while a 50 percentage point increase in cumulative amortisation is associated with a subhazard that is around 0.6 times lower. Of course, income is also likely to play a role in this relationship; borrowers with higher incomes can pay down their loans faster than other borrowers and will be less likely to enter arrears for other reasons related to their higher income.
One caveat with these results (and the results from the model more generally) is that, given that we do not have data on borrower incomes, we cannot construct a meaningful measure of borrowers' debt-servicing burdens. Therefore, the estimated relationship between the LVR at origination (or the amount of amortisation) and the incidence of arrears may be biased due to the unobserved effect of debt-servicing burdens. Although the estimated required payment should partly control for this, ideally the required payment should be scaled by the borrower's income, since borrowers with higher incomes should be able to meet higher payments.
The SHR for dwelling price growth since loan origination is not statistically significant, suggesting that changes in dwelling prices have not been associated with changes in the incidence of arrears in this sample. This may reflect a lack of sufficient variability in dwelling prices in the sample period. It could also reflect measurement error, since borrowers who entered arrears in this sample may have experienced changes in dwelling prices that were different to the path of dwelling prices implied by the indices that we have used.
2.3.2 Ability-to-pay factors
The results suggest that borrowers with higher mortgage interest rates have a higher subhazard of entering arrears; a loan with an interest rate 1 percentage point higher than that of an otherwise identical loan is estimated to have a subhazard of entering arrears that is around 1.4 times higher. The mechanism through which this effect might be expected to work is that the higher interest rate increases the required payment, making it more likely that the borrower's income is insufficient to cover their loan payments and subsistence-level expenditure. However, our model controls for the estimated required payment, suggesting that the effect of interest rates on arrears in the model is not just due to such a ‘debt-servicing channel’. Instead, the estimated effect may reflect the fact that lenders charge higher interest rates on loans that are more likely to fall into arrears (i.e. higher-risk loans) as compensation for this risk. In our model, we are able to control for some observable loan risk characteristics, such as the loan documentation type. However, when negotiating a borrower's interest rate, lenders may also take into account variables that do not appear in this dataset, such as the borrower's income or wealth; additionally, the lender's existing relationship with the borrower is likely to be an important factor.[9] Overall, the estimated relationship between the mortgage interest rate and the probability of entering arrears is consistent with lenders using risk-based pricing.
The results suggest that ability-to-pay shocks, proxied by the local unemployment rate, have a small but statistically significant (at the 10 per cent level) correlation with the probability of entering arrears. This estimate almost certainly understates the effect of a borrower actually becoming unemployed on the probability that they enter arrears. Indeed, Gyourko and Tracy (2013) show that using unemployment rates to proxy for borrowers' actual (unobserved) employment statuses can result in a severe attenuation bias. This is supported to some extent by our analysis in Section 3 using the separate household-level dataset in which we observe each borrower's labour force status directly.
2.3.3 Loan characteristics
In terms of loan characteristics, fixed-rate and interest-only loans are estimated to have lower subhazards of entering arrears than variable-rate and amortising loans, respectively. While borrowers on fixed-rate loans are insulated against changes in lending rates during their fixed-rate period, our model includes the mortgage interest rate and the estimated required payment, so it is unclear why fixed-rate borrowers should be less likely to fall into arrears. The estimated subhazards for fixed-rate and interest-only loans are possibly biased to the extent that the take-up of fixed-rate and interest-only loans is correlated with income (and potentially with other omitted variables, such as financial sophistication). Another possibility is that these loans tend to enter arrears only after they ‘reset’ to variable rates (in the case of fixed-rate loans) or amortising payments (in the case of interest-only loans). However, estimating a version of the model that only uses the characteristics of the loan as at loan origination yields very similar results.
Despite the results suggesting that interest-only and fixed-rate loans are less likely to enter arrears than other loans, it is important to remember that these results are conditional on cumulative amortisation. To the extent that these loans amortise more slowly than other loans, increases in these types of loans can represent increasing risk, as the results suggest that slower rates of amortisation are associated with a higher probability of entering arrears. Loans that amortise more slowly may also generate greater loan losses for lenders if those loans default.
Also relating to loan characteristics, the results indicate that low-doc loans (that is, loans where the borrower's income has not been documented, assessed and verified, such as by checking pay slips or business activity statements) have a subhazard of entering arrears that is around 1.8 times greater than that of full-doc loans, after controlling for other factors. This does not simply reflect the tendency for low-doc loans to be extended to self-employed borrowers, who tend to have more volatile incomes, as we control for whether the borrower was self-employed at the time of loan origination.[10] The estimated SHR for low-doc loans could reflect a correlation with the level of borrower income, but could also reflect higher-risk borrowers self-selecting into this product category. The results also suggest that refinanced loans have a subhazard of entering arrears that is 1.8 times that of loans for property purchase. This could reflect the fact that some borrowers refinance because they are having difficulty making their payments, implying that there is also self-selection of some riskier borrowers into this loan type.
2.3.4 Economic significance
A potentially useful way to consider the economic significance of these results is by examining the cumulative incidence function (CIF), which gives the probability of a loan entering arrears before time t (for technical details, see Appendix C). Figure 2 plots the CIF for hypothetical loans with different characteristics.[11] The characteristics of the ‘base’ loan are the modes of the categorical variables and the means of the continuous variables (see note to Figure 2 for details), while the other series show how the probability of entering arrears changes as certain loan characteristics vary from the base case.
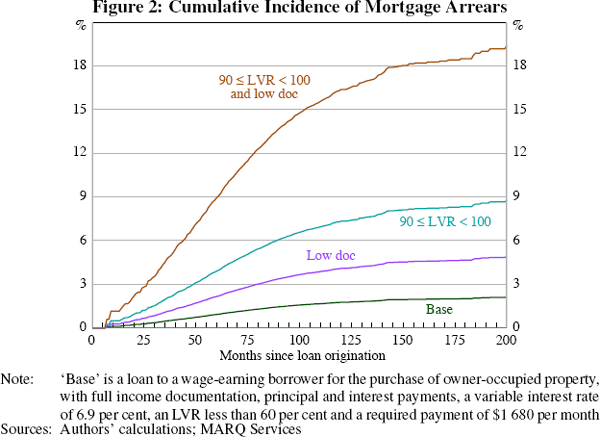
The probability that the base loan enters arrears within the first five years is 0.9 per cent. A low-doc loan that is otherwise identical to the base loan has a probability of entering arrears in the first five years of 2.2 per cent, while a loan with an LVR between 90 and 100 per cent at origination has a probability of around 3.9 per cent. A loan that is low doc and has a high LVR at origination is much more likely to enter arrears than a loan with just one of these characteristics; 8.9 per cent of these loans would be expected to enter arrears in the first five years.
Footnotes
Details on how the dataset is cleaned and constructed are available from the authors on request. [3]
The average number of observations per loan is substantially smaller than the length of the sample period (which spans around 50 months). This is because some loans enter the loan pool after the beginning of the sample period in 2009 and some loans are repaid early (and thus drop out of the sample). [4]
The arrears rate on loans with an LVR greater than 100 per cent at origination is lower than on loans with an LVR between 60 and 100 per cent at origination. However, the dataset contains information on only the first property securing each loan, implying that loans with multiple properties as security will have an LVR at origination that is overestimated. [5]
For the random time-to-event variable T, h(t) = limδ→0 {Pr(t ≤ T < t+δ|T ≥ t)/δ}. [6]
These transition rates should not be taken as indicative of typical rates of transition out of arrears for the population of housing loans. Transition rates may vary across lenders based on their processes for collections and their procedures for dealing with customers experiencing financial hardship. They may also vary across time due to changes in these processes and procedures or as a result of macroeconomic factors. [7]
Results from an alternative model that accounts for the discrete timing of observations in the dataset and for unobserved heterogeneity (but ignores the presence of the competing risk) are presented in Appendix D. These results are broadly similar to the results from the competing risks model. [8]
Based on a linear regression, the relevant loan characteristics available in the sample (e.g. loan size, loan documentation type, interest rate type and LVR at origination) explain only around 35 per cent of the variation in the difference between the interest rate for each loan and the advertised standard variable rate for the corresponding lender. [9]
Around 80 per cent of low-documentation loans in the sample were to borrowers that were self-employed when the loan was approved. [10]
The CIFs are calculated based on the results of an alternative competing risk model that only uses information from the time of loan origination. This model excludes cumulative amortisation, dwelling price growth and the local unemployment rate. [11]