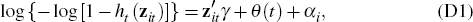RDP 2014-13: Mortgage-related Financial Difficulties: Evidence from Australian Micro-level Data Appendix D: Discrete-time Duration Model with Unobserved Heterogeneity
November 2014 – ISSN 1320-7229 (Print), ISSN 1448-5109 (Online)
- Download the Paper 728KB
One assumption underlying the competing risks model is that the time between loan origination and a loan entering arrears is continuous – that is, that we observe the exact time that a loan enters arrears. However, in reality, we only observe the loans at the end of each month and, consequently, the data are discrete. This suggests that a discrete-time duration model may be more appropriate. Another aspect of our competing risks model, which is discussed in Section 2.2, is that we do not allow loans in arrears to cure or enter arrears multiple times. However, if we were to relax this assumption and use information on loans that enter arrears multiple times, we could potentially control for unobserved heterogeneity across loans. We consider these alternative model features as a robustness check of the results from our competing risks regression.
It can be shown that a continuous-time duration model with a proportional hazards representation can be expressed as a complementary log-log regression if the observations are discretised (e.g. Kaplan 2012). The model, which includes a normally distributed random effect to allow for unobserved heterogeneity, can be written as:
where ht (zit) is the hazard of entering arrears during month t, θ(t) is the integrated baseline hazard during month t, which we proxy for using a polynomial in loan age, and αi is a random effect for loan i. We estimate this model using the xtcloglog function in Stata 13 and report exponentiated coefficients, which can be interpreted in a similar fashion as the subhazard ratios presented in Section 2.3. For the purposes of this analysis, we abstract from the presence of the competing risk of full payment.
While there are some differences between the results from this model and the results from our competing risks model, overall the key results are qualitatively similar (Table D1). The hazard of entering arrears tends to increase with the LVR at origination, although, like in the competing risks model, it falls for loans with an LVR at origination greater than 100 per cent. Increases in amortisation since origination decrease the hazard of entering arrears. However, in contrast to the results from the competing risks model, increases in dwelling prices significantly decrease the hazard of entering arrears. Investor loans are also significantly less likely to enter arrears than owner-occupier loans.
| Explanatory variable | exp(γ) | Explanatory variable | exp(γ) |
|---|---|---|---|
| Amortisation | 0.98*** | Investor | 0.78*** |
| LVR at origination | Loan purpose | ||
| 60 ≤ LVR < 80 | 2.35*** | Home improvement | 0.42*** |
| 80 ≤ LVR < 90 | 2.80*** | Refinance | 2.08*** |
| 90 ≤ LVR < 100 | 5.97*** | Other | 1.15 |
| LVR ≥ 100 | 5.04*** | Local unemployment rate | 1.02 |
| Dwelling price growth | 0.98*** | Low doc | 3.49*** |
| Fixed rate | 0.36*** | Minimum required payment | 1.07*** |
| Interest only | 0.61*** | Self-employed | 1.36** |
| Interest rate | 1.42*** | ||
| Number of observations | 1,624,132 | ||
| Number of loans | 63,526 | ||
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively; standard errors are clustered by loan; model includes a random effect for each loan; ‘amortisation’ is the percentage decrease in the loan balance since origination; ‘dwelling price growth’ is the cumulative percentage growth of dwelling prices since origination; ‘minimum required payment’ is measured in thousands of dollars Sources: ABS; APM; Authors' calculations; MARQ Services; RP Data-Rismark |
|||
Although this model provides a potentially useful robustness check for the results from our competing risks model, it is worth noting that the model has two key shortcomings:
- It ignores the presence of the competing risk of full payment, potentially resulting in misleading estimates.
- It assumes that the loan-level random effect is uncorrelated with the take-up of particular loan features. This seems unlikely if the random effect captures the time-invariant component of omitted factors such as income and financial sophistication.