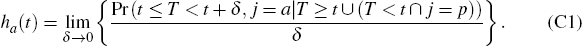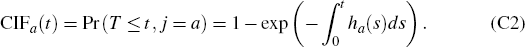RDP 2014-13: Mortgage-related Financial Difficulties: Evidence from Australian Micro-level Data Appendix C: The Competing Risks Regression Model

Let j index events, with j = a corresponding to a loan falling into arrears (i.e. the event of interest) and j = p corresponding to the loan being paid down in full (i.e. the competing risk). The subhazard for entering arrears is then:

The subhazard is similar to the hazard function from standard duration analysis, except that it keeps loans that have been paid down in full ‘at risk’ of entering arrears so that they can be appropriately counted as having zero probability of entering arrears. While the subhazard is somewhat difficult to interpret (in fact, Fine and Gray (1999) describe the ‘risk set’ associated with this subhazard as being ‘unnatural’), it provides a convenient way to model the CIF, which gives the probability of a loan falling into arrears before time t (Rodriguez 2012):

One of the advantages of using this competing risks regression approach is that the covariates included in the model will have effects on the subhazard and the CIF that are in the same direction. This is not necessarily the case when modelling the event of interest using a standard duration model, such as a Cox proportional hazard model, which treats the competing risk as a censoring event; the effect of a covariate on the CIF will depend on how it affects the incidence of the event of interest, but also on how it affects the incidence of the competing risk.

The model is estimated using the stcrreg command in Stata 13. Parameter estimates are obtained by maximising a log-pseudolikelihood function, and standard errors are clustered by loan.