RDP 2024-05: Sign Restrictions and Supply-demand Decompositions of Infation 3. What Do Sign Restrictions Tell Us about Decompositions?
August 2024
- Download the Paper 1.49MB
This section analytically characterises identified sets for particular structural parameters under sign restrictions on the slopes of supply and demand curves, closely following Baumeister and Hamilton (2015). I use this characterisation to discuss features of the sets of decompositions that are consistent with the restrictions, including conditions under which these sets are (un)informative about the decompositions.
3.1 Sign restrictions and identified sets
Let vech. The correlation between the innovations in pt and qt is
so controls whether the correlation is positive or negative . The space of 2 × 2 orthonormal matrices can be represented as
where (e.g. Baumeister and Hamilton 2015).
In the absence of identifying restrictions, the identified set for (the matrix of impact impulse responses) is
Consider imposing the following pattern of sign restrictions on :
These restrictions require pt and qt to move in opposite directions in response to the first shock and in the same direction in response to the second shock. Therefore, the first shock can be interpreted as a supply shock and the second shock can be interpreted as a demand shock. Accordingly, I henceforth write to represent the supply shock and to represent the demand shock. This means that FEVDh represents the contribution of the supply shock to the horizon-h FEV of pt and Ht,t+h represents the contribution of the supply shock to the (h + 1)-step-ahead forecast error in pt.
The identified set for under the sign restrictions is[11]
This identified set is identical under the following pattern of restrictions on A0:
which imply that the first equation of the SVAR describes an upward-sloping (i.e. supply) curve and the second describes a downward-sloping (i.e. demand) curve.
The structural shocks and reduced-form innovations are related via . We can think of this system of equations as describing the ‘short-run’ supply and demand curves. The slopes of these supply and demand curves are useful for understanding the conditions under which the sign restrictions are informative about the decompositions. I therefore present the identified sets for the slopes of these curves below, but these results are not new; for similar results, see Leamer (1981), Baumeister and Hamilton (2015) or Uhlig (2017). In the absence of identifying restrictions, the identified set for A0 is
The slopes of the supply and demand curves are the coefficients on uqt in each equation after normalising the coefficients on upt to one.
Let represent the slope of the supply curve:
It is straightforward to show that the identified set for is
If the forecast errors are negatively correlated, the sign restrictions do not reveal anything about the slope of the supply curve. If the forecast errors are positively correlated, it is possible to bound the slope of the supply curve. The informativeness of these bounds depends on how strongly the forecast errors are correlated; as approaches one, the lower and upper bounds of the identified set converge to the same value. Intuitively, when the forecast errors are strongly positively correlated, the observed forecast errors approximately trace out the supply curve.
Similarly, the slope of the demand curve is
and the identified set for is
If the forecast errors are positively correlated, the sign restrictions reveal nothing about the slope of the demand curve. In contrast, when the forecast errors are negatively correlated, the sign restrictions generate informative bounds for the slope of the demand curve, which shrink to a point as approaches minus one, in which case the forecast errors trace out the demand curve.
Figure 1 illustrates this reasoning using simulated data where the forecast errors are strongly negatively correlated. The strong negative correlation means that the forecast errors trace out the demand curve, but there is a wide range of supply curves that are consistent with the data. At one extreme, the observed forecast errors could have been generated by shifts in a vertical supply curve (corresponding to ) along the demand curve. At the other extreme, they could have been generated by shifts in a horizontal supply curve (corresponding to ). Any intermediate case between these two extremes is consistent with the sign restrictions and observed forecast errors.
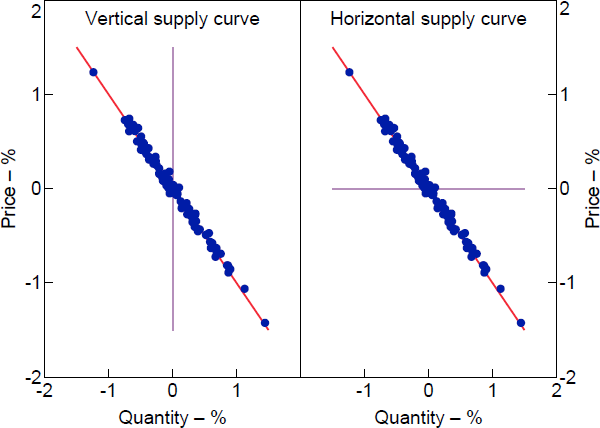
Note: Dots represent forecast errors in price and quantity; red line is demand curve; lilac line is supply curve.
3.2 Historical decomposition
In this two-variable model, we can write the historical decomposition of pt with respect to the supply shock, Ht,t+h, as a function of and :
where
The identified set for in Equation (12) induces a set of values for the historical decompositions that are consistent with the reduced-form parameters and the observed data. I refer to this set of values as the conditional identified set for Ht,t+h:[12]
where is the lower bound of the conditional identified set and is the upper bound.[13] Any value of Ht,t+h lying within is equally consistent with the identifying restrictions, the joint distribution of the data (as summarised by ) and the observed forecast errors.
The value of that attains the lower or upper bound of may differ across t. The model corresponding to the lower or upper bound may thus differ, implying that the bounds correspond to supply or demand curves with different slopes in different periods. However, because every model – and thus decomposition – in the set is equally consistent with the data, the models that attain the bounds should not be given particular prominence over any other model within the identified set.
3.2.1 Computation
can be computed by solving the optimisation problems that define and . Focusing on the upper bound, corresponds to either an end point of or a critical point of in the interior of . Evaluating at the end points of is straightforward given that an analytical expression for is available. Rewriting the historical decomposition as a function of q1, the problem subject to has first-order necessary condition where is the Lagrange multiplier on the constraint. Solutions to this equation are eigenvectors of . I compute the (two) eigenvectors, normalise their signs so that the sign normalisation is satisfied, and check whether the normalised eigenvector lies within . is then obtained by direct comparison of the function values at the end points and admissible critical points (if any). is obtained similarly.
3.2.2 A special case
Consider the case where interest is in the contribution of the supply shock to the one-step-ahead forecast error in pt, so h = 0. It can be shown directly that
This expression is equivalent to when shocks have non-zero effects only on impact, in which case for all l > 0. We can therefore use this expression to draw some useful intuition about the conditions under which the sign restrictions are informative about historical decompositions, with the qualification that when interest is in definitions of the historical decomposition other than Ht,t (e.g. H1,t), the intuition is approximate (or may break down) when the effects of shocks are persistent.
The set of historical decompositions always admits ‘extreme’ contributions. When , and . That is, when the forecast errors in pt and qt are negatively correlated, the restrictions always admit the possibility that the supply shock is entirely responsible for the unexpected change in pt . Intuitively, this is because the restrictions always admit the two extreme models in which the supply curve is vertical or horizontal. Conversely, when and . So, when the forecast errors in pt and qt are positively correlated, the restrictions always admit the possibility that a supply shock is responsible for none of the unexpected change in pt . This is because the restrictions admit the two extremes where the demand curve is vertical or horizontal.
The set of historical decompositions is uninformative when innovations are weakly correlated. If . In this case, both 0 and upt lie within . The set of contributions is therefore consistent with forecast errors being driven entirely by a demand shock or entirely by a supply shock. The intuition is that uncorrelated innovations are equally consistent with a vertical supply curve and a horizontal demand curve , in which case forecast errors are purely driven by demand shocks, or with a horizontal supply curve and a vertical demand curve , in which case forecast errors are purely driven by supply shocks. Any observed forecast errors can be explained by either of these extreme cases.
The set of historical decompositions can be very informative when forecast errors are strongly correlated. When the forecast errors are strongly negatively correlated, they trace out the demand curve, and forecast errors predominantly reflect supply shocks. However, we learn very little about the shape of the supply curve; the same forecast errors could be generated by shocks to a supply curve that is very steep, very flat, or something in between (see Figure 1). If we observe forecast errors that are consistent with the historical negative relationship, then we can conclude that they were mainly driven by a supply shock (even though we do not know much about the shape of the supply curve), so the set of historical decompositions is narrow around the observed forecast error. Similar reasoning applies when the forecast errors are strongly positively correlated, except in that case the forecast errors trace out the supply curve and forecast errors are attributable to demand shocks.
To illustrate this case, the top panels of Figure 2 plot two potential shifts in the supply curve that could have generated a particular forecast error – specifically, a roughly 1.5 per cent fall in price and 1.5 per cent increase in quantity. The forecast error can, at one extreme, be completely explained by a shift in a vertical supply curve (top left panel) or, at the other extreme, a shift in a horizontal supply curve (top right panel). Shifts in supply curves with any intermediate slope are also compatible with the observed forecast error. Despite not knowing anything about the slope of the supply curve, the contribution of the supply shock to the forecast error in prices is pinned down to be (approximately) equal to the observed forecast error – that is, the supply shock contributed 1.5 percentage points to the unexpected decline in prices.
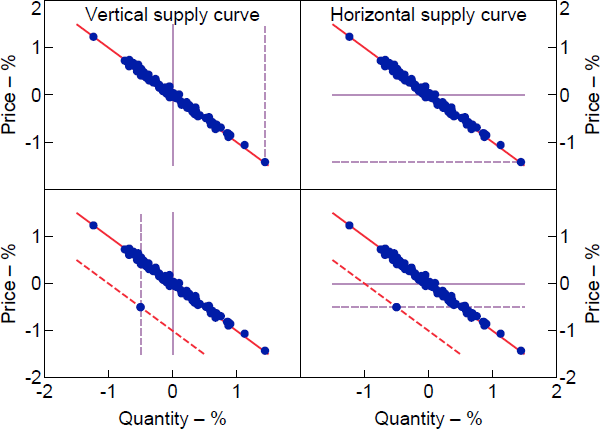
Notes: Dots represent forecast errors in price and quantity; red line is demand curve; lilac line is supply curve. Dashed lines represent shifts in supply and demand curves that could explain particular forecast errors.
But the set of historical decompositions can also be very uninformative even when forecast errors are strongly correlated. If the forecast errors are strongly negatively correlated but we observe forecast errors that depart from the historical negative relationship, the set of historical decompositions may be wide and thus economically uninformative. The bottom panels of Figure 2 illustrate the reasoning. In the left panel, a 0.5 per cent fall in both price and quantity can be explained by the combination of a negative demand shock (a downward shift in the demand curve from the solid to dashed red line) and a negative shock to a vertical supply curve (a leftward shift in the supply curve from the solid to dashed lilac line). In this case, the contribution of the supply shock to the forecast error in pt is 0.5 percentage points. Alternatively, as illustrated in the right panel, the forecast error can be explained by a combination of the same negative demand shock and a negative shock to a horizontal supply curve. In this case, the contribution of the supply shock to the forecast error in pt is −0.5 percentage points. Shifts in supply curves with slopes that lie between these two extremes are also consistent with the forecast error. The conditional identified set for the historical decomposition is therefore . One intermediate case (not plotted) is where the forecast error is driven entirely by a negative demand shock shifting the demand curve along a supply curve with gradient one, in which case the contribution of the supply shock is zero.
3.3 Forecast error variance decomposition
We can rewrite FEVDh as
where
The identified set for is then defined as
where is the lower bound of the identified set and is the upper bound.[14] Any value of FEVDh lying within is equally consistent with the identifying restrictions and the second moments of the data, as summarised by . As in the case of the historical decomposition, the bounds of may be attained by different values of (i.e. models) at different horizons.
Computation of proceeds similarly to the case where the historical decomposition is the quantity of interest (described in Section 3.2.1). The problem subject to has first-order necessary condition , where is the Lagrange multiplier on the constraint. Solutions to this equation are eigenvectors of .[15]
3.3.1 A special case
Consider the case where interest is in the one-step-ahead FEVD of pt with respect to the supply shock, FEVD0. The contribution of to the FEV of pt is (i.e. the square of the impact impulse response of pt to a standard deviation supply shock). Since the one-step-ahead FEV of y1t is , the contribution of to the FEV as a fraction of the total FEV is .
When , the upper bound of is zero, so attains its maximum of one and . is strictly increasing for , so occurs at the lower bound of . When is bounded above by zero and has lower bound therefore achieves its minimum value of zero at and is strictly increasing for , so occurs at the upper bound of . Putting this together and rewriting the bounds in terms of , the identified set for FEVD0 is
Echoing the analysis of the historical decomposition, the sign restrictions always admit extreme values of the FEVD. When , the sign restrictions always admit the possibility that the supply shock explains all of the variance of upt (because the supply curve may be horizontal) and when they always admit the possibility that the supply shock explains none of the variance (because the demand curve may be horizontal). As approaches [0, 1], in which case the restrictions are completely uninformative.
The sign restrictions become more informative as the magnitude of the correlation between forecast errors, , increases. collapses to one as ; intuitively, if the one-step-ahead forecast errors are close to perfectly negatively correlated, the forecast errors must be generated by supply shocks shifting the supply curve along a static demand curve (see Figure 1). Conversely, converges to zero as ; if the one-step-ahead forecast errors are close to perfectly positively correlated, the forecast errors must be generated by demand shocks shifting the demand curve along a static supply curve. To conclude unambiguously which shock is driving most of the variation in prices, it is necessary that when , supply shocks account for at least half the variance of prices, whereas when demand shocks account for at least half the variance of prices.[16]
Footnotes
For a derivation of this identified set, see Baumeister and Hamilton (2015) or Read (2022). [11]
The historical decomposition is a function of the realisation of the data in period t (via the reduced-form innovations), so the standard concept of an identified set does not apply; see Giacomini, Kitagawa and Read (2023) for a discussion of this point in the context of SVARs identified via narrative restrictions. [12]
The same reasoning underlies implementation of the ‘max share’ approach to identification, which involves finding the ‘shock’ with maximal contribution to a particular FEV (e.g. Uhlig 2003; Angeletos, Collard and Dellas 2020; Carriero and Volpicella forthcoming). [15]