RDP 2023-03: Doing Less, with Less: Capital Misallocation, Investment and the Productivity Slowdown in Australia 4. Has Capital Reallocation Slowed?
March 2023
- Download the Paper 1.26MB
4.1 Empirical framework
To investigate whether the link between firm capital growth and productivity has changed, we apply the model outlined by Decker et al (2020) for estimating the responsiveness of firm growth (employment or capital) to productivity. Their approach is motivated by canonical models of firm dynamics, which predict that conditional on initial size, more productive firms should grow more quickly than less productive firms.
In particular, Decker et al (2020) show that for a broad range of models with a decreasing returns to scale revenue function due to decreasing returns to scale production or inelastic demand:
employment growth will be increasing in the level of productivity (MFPi,t), conditional on initial firm size Ei,t−1 (which captures past productivity as well as other past factors influencing employment):
Taking a simple first-order log-linear approximation yields:
The coefficient captures how responsive employment growth will be to productivity. This will be affected by a number of factors, including any costs in adjusting the firm's labour (see Section 5).
As in Decker et al (2020), this same model can be extended to capital and investment. As such, the basic set-up of our regression model is:
where future growth is a function of current log productivity (MFP) of firm i at time t, expressed as a deviation from the industry average. This means that we are abstracting from differences in productivity levels across sectors, and focusing on high- versus low-productivity firms as defined within industries. Finally, the vector X includes controls for initial firm size and age (a dummy for young firms below five years old), past firm sales growth, industry-by-time fixed effects, and the (demeaned) state unemployment rates alone and interacted with productivity.
Our measure of capital growth is defined as the change in the capital stock divided by the average capital stock across both periods following Davis, Haltiwanger and Schuh (1996):
where Ki,t is the capital stock of firm i in period t. This measure is bounded between −2 and 2 and it is a second-order approximation of the log difference for growth rates around zero. Further it can accommodate growth of entering and exiting firms, in which case the function takes a value of 2 (entry; Kt = 0) or −2 (exit; Kt+1 = 0). However, for our purposes we focus on the intensive margin and abstract from entry and exit given Andrews and Hansell (2021) already explored the exit margin.[5]
Since our aim is to identify how productivity-enhancing reallocation is evolving in a structural sense, the model controls for cyclical influences in three key ways. First, we control for time-varying shocks at a four-digit ANZSIC 2006 level (the finest possible level of industry classification). This will capture any shocks hitting the industry that might influence investment and firm performance overall. Second, the inclusion of the state unemployment rate directly controls for state-level business cycles. And finally, by interacting state-level unemployment with productivity we control for any cyclicality in the responsiveness of capital growth to firm productivity.[6]
Across all versions of the baseline model we are interested in the sign and significance of the coefficient on productivity, . If positive and significant, we can infer that capital flows to more productive firms at the expense of less productive firms within industries, indicating that the process of capital reallocation is productivity enhancing, even after controlling for a range of cyclical influences.
We can then extend this model to allow the coefficient on productivity to vary across periods. In particular, we examine whether the coefficient changes during the global financial crisis (GFC) (2007/08 to 2010/11), and post-GFC (2011/12 to 2016/17).
This is not the only approach to considering static and dynamic allocative efficiency. Hsieh and Klenow (2009) use the dispersion in measured revenue-based MFP, assuming that any dispersion indicates a misallocation of resources. However, recent research argues that this only holds under a fairly restrictive set of assumptions that equalise marginal quantity-based MFP and average revenue-based MFP. If the assumptions do not hold, the measured dispersion reflects noise, as well as any true misallocation (Haltiwanger, Kulick and Syverson 2018). Other approaches, such as Baqaee and Fahri (2020), take a more structural approach. However, we follow the approach of Decker et al (2020) given its parsimony, transparency and robustness, and to be consistent with previous analysis.
4.2 Baseline results
Table 1 shows the results from the baseline model. As evident in columns 1 and 2, the coefficient on productivity is positive, indicating that more productive firms tend to grow their capital stocks more quickly, meaning capital appears to flow from less to more productive firms (as a share of total capital). However, as evident in column 2, the speed of the reallocation seems to have slowed in the most recent period.
| Non-current assets | Non-current assets | FTE | |
|---|---|---|---|
| Productivity | 0.022*** (0.004) |
0.036*** (0.007) |
0.179*** (0.013) |
| GFC*Productivity | −0.001 (0.008) |
−0.065*** (0.007) |
|
| Post-GFC*Productivity | −0.024*** (0.008) |
−0.093*** (0.007) |
|
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Size | Y | Y | Y |
| Age | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,048,427 | 2,048,427 | 2,048,427 |
| Adj R-squared | 0.031 | 0.031 | 0.050 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
|||
To provide some sense of the magnitude, pre-GFC the model implies that a more productive firm (one standard deviation above the industry mean) would grow its capital stock around 7.2 percentage points faster than a low-productivity firm (one standard deviation below the mean). However, this gap fell to 2.4 percentage points, or by around two-thirds.
To get a sense of whether labour or capital reallocation has slowed by more, we re-run the model looking at growth in employment. The results in column 3 show that the rate of productivity-enhancing labour reallocation has declined by a slightly smaller amount, approximately halving over the period. So the relationship between capital growth and productivity has weakened slightly more than employment and productivity, though the two do not differ substantially.
We also run the baseline model in column 2 of Table 1 but replacing MFP with an indicator capturing where in the industry productivity distribution the firm sat in year t (by quartile). This allows for a more flexible, non-parametric treatment that could be more robust than the linear relationship assumed above. Figure 4 shows the result. We see that over time the gap in capital growth between the least productive firms and other firms has narrowed, particularly for the most productive quartile.
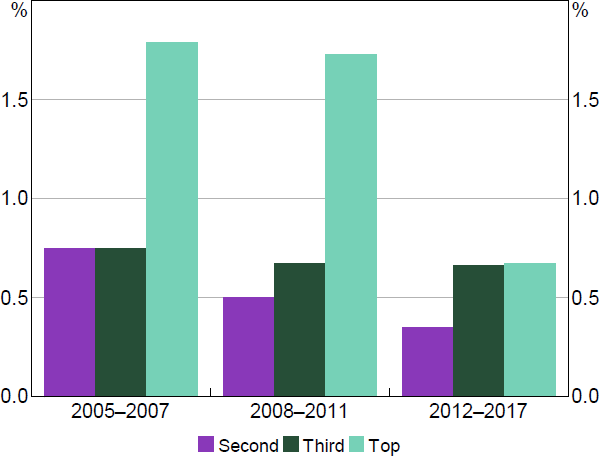
Note: Based on bounded capital growth rate.
One interpretation is that Australian capital accumulation over the course of the productivity slowdown can be characterised as ‘doing less, with less’: not only are firms doing less investment, but the investment that is undertaken is likely lower yielding. This raises the prospect that there is an allocative dimension to the business investment slowdown and that the frictions impeding Australian economic dynamism have infected capital deepening as well as MFP.
We consider five further robustness checks. First, we consider the possibility that measurement error or similar issues could introduce endogeneity, given the capital stock enters the production function, and so is used to estimate (lagged) MFP, but it also enters capital growth (division bias). For example, if a firm re-valued an asset, this could flow through to measured investment and MFP. To account for this we try two different capital growth measures (while continuing to use our baseline capital stock measure in the MFP estimation). The first is a PIM-based capital stock measure. The second is gross investment, scaled by lagged total capital. The use of gross investment also links the analysis more directly to the observed slowdown in aggregate investment.[7] As shown in Table B1, the results are similar using these metrics.
Second, we remove the primary sector, agriculture and mining, to ensure it is not driving the results. Measurement of investment and the capital stock in this sector could be subject to greater mismeasurement due to the important role of land in production, while the mining boom may also affect outcomes. The results are robust to removing the primary sector (Table B2).[8]
The third robustness test is to consider whether the dynamic nature of investment could affect our results. Investments could take place over multiple years, or could be lumpy with firms making large investments one year then very little in the following years (e.g. Bond and Van Reenen 2007; Hambur and La Cava 2018). To account for such dynamics, we extend the regression in Table 1 to include the lagged capital stock or growth, and allow their coefficients to change over time as with productivity, as done in Decker et al (2020). Doing so does not change the results (Table B3).[9] Relatedly, we also consider whether the persistence of productivity shocks may have declined, which could make firms less responsive given the lumpy and irreversible nature of investment. However, there is no substantive evidence of such a change (Table B4).
Fourth, we remove firms that are considered small for tax purposes, below $2 million in turnover, to abstract from changes in tax incentives that may have influenced investment behaviour (Table B5). The results are largely unchanged.
Finally, the translog production function could be a problem. The advantage of a translog over a Cobb-Douglas function is that it allows for the possibility that large firms may have different production technologies to small firms. However, the model may be ‘overfitting’, potentially making large high-productivity firms look less productive (for example). As such, we also run the baseline model using MFP estimates from a Cobb-Douglas production function and find similar results (Table B6).
To get some initial indications of why the relationship between productivity and capital growth weakened, we re-estimate the model over sub-samples of young and older firms (above or below five years old). To do so we use a simpler measure of (log) capital productivity, as MFP estimation requires several years of data, meaning that the sample of young firms for whom we have MFP estimates is relatively small.
The results are shown in Table 2. The first thing to note is that the relationship between productivity and capital growth appears stronger for young firms, consistent with these firms being in an ‘up or out’ stage of their development, where they are experimenting and succeeding, or failing and exiting. The second thing to note is that the weakening of the relationship between productivity and capital growth is more notable for older firms. This suggest that the slowdown in reallocation does not simply reflect a compositional shift towards older firms in the economy as entry rates have fallen, though that will have contributed. Rather the slowdown appears to be ‘within’ both older incumbent and younger firms. This finding is robust to using MFP, though the sample of young firms decreases substantially (Table B7).
| Young | Old | |
|---|---|---|
| Productivity | 0.123*** (0.003) |
0.064*** (0.002) |
| GFC*Productivity | −0.003 (0.002) |
−0.004*** (0.001) |
| Post-GFC*Productivity | −0.011*** (0.003) |
−0.019*** (0.001) |
| Controls | ||
| Industry*Year | Y | Y |
| State*Year | Y | Y |
| State unemp*Productivity | Y | Y |
| Age | Y | Y |
| Size | Y | Y |
| Sales growth | N | N |
| Observations | 460,740 | 2,143,518 |
| Adj R-squared | 0.115 | 0.038 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. ‘Young’ is firms 0-5 years of age, ‘Old’ over 5 years of age. Lagged sales growth variable removed to increase sample of small firms. |
||
Footnotes
Note that given our MFP measure uses capital stock at the start of the period, Ki,t−1, as an input the timing conventions are the same as used in Decker et al (2020). [5]
We find evidence that capital reallocation is countercyclical, while labour reallocation is procyclical. Still the magnitude of the coefficients is quite small, with around a 2 and 4 percentage point change in unemployment being required, respectively, to equate to the ‘structural’ slowdown that we document in this paper. [6]
Note that for this specification we are effectively lagging MFP given the timing conventions to minimise model changes. [7]
Table B9 also shows the results by ANZSIC division, though the results are not significant for any division, likely reflecting the much smaller samples. [8]
This approach also more directly captures initial size compared to size dummies used elsewhere. [9]