Research Discussion Paper – RDP 2023-03 Doing Less, with Less: Capital Misallocation, Investment and the Productivity Slowdown in Australia
1. Introduction
Labour productivity growth is the key driver of living standards over the medium term. However, growth in labour productivity has slowed markedly over recent decades in Australia and other advanced economies. If this slower rate of growth is maintained, it will have negative implications for living standards and the budget position. It will also make it harder to conduct monetary policy, as it will mean lower potential growth and real neutral interest rates, increasing the likelihood that nominal interest rates hit the effective lower bound.
While a range of explanations for weak productivity growth have been advanced, credible accounts of the Australian productivity slowdown capture two empirical regularities.[1] First, non-mining investment was weaker than might have been expected based on economic fundamentals over much of the 2010s (e.g. Heads of Treasuries 2017; Debelle 2017; van der Merwe et al 2018; Hambur and Jenner 2019). This low level of non-mining investment occurred despite declines in interest rates and the end of the mining investment boom which likely freed up capital for non-mining investment. With less investment, the capital stock per worker grows more slowly, and so does output per worker and therefore productivity growth.
Second, there has been a pervasive decline in economic dynamism since the mid-2000s (e.g. e61 2022). Firms and product markets have become more stagnant: firms are less likely to enter and exit, the largest firms in industries have become more entrenched, and market concentration and mark-ups have increased. And labour markets have also become less fluid: job mobility and labour reallocation rates have declined, and labour has become less likely to flow to more productive firms.[2]
The decline in dynamism has meant that scarce labour is increasingly ‘trapped’ in lower productivity firms, lowering both labour productivity (how productively the economy uses its labour) and likely multifactor productivity (MFP; how productively it uses all resources). For example, Andrews and Hansell (2021) found that the pace at which labour is reallocated from low- to high-productivity firms has slowed since 2012, and that this can account for a quarter of the slowdown in labour productivity growth from 2012 to 2016. This slowdown in reallocation was worse in industries where competitive pressures declined (Hambur forthcoming).
To date, studies have looked at these two facts – weak investment and declining dynamism – in isolation, but they could be linked. If the economy is growing more slowly due to slower productivity growth, productive firms may not feel the need to invest as much to keep up with demand and maintain market share. Similarly, if there are frictions that prevent productive firms from expanding their workforce, they could also cause them to invest less.
As such, this paper tries to bring these two observations together to gain a greater understanding of both. In particular, it explores three questions:
- Could the same factors that are driving slower dynamism and reallocation also be driving weaker investment?
- Has the reallocation of capital (financial or physical) from less to more productive firms (within industries) slowed, as has been evident with labour? If so, not only is investment weak, but it is being put to less productive uses.
- By focusing on capital reallocation and investment, can we gain additional insights into slowing economic dynamism?
To preview the results, the answer to all three questions is yes. Declines in investment, while broad based, have been more notable for the more productive firms within each industry, suggesting that whatever is inhibiting productive firms from investing is also holding back aggregate investment. Consistent with this, the reallocation of capital from less to more productive firms in an industry has slowed moderately since the mid-2000s, meaning capital has increasingly been allocated to less productive uses. A simple counterfactual exercise suggests that, had the flow of labour and capital towards more productive firms not slowed over the period since the mid-2000s, and therefore had more productive firms been larger, by 2017 the economy would have been $13 billion (or ¾ per cent of GDP) larger, equating to around $550 per person or $1,000 per worker. And this only captures one channel through which weaker capital reallocation and dynamism are likely to have affected incomes, abstracting from any effects on the size of the capital stock, or on innovation and firm-level productivity. Thus, the story of Australian capital accumulation over the past decade or so is one of ‘doing less, with less’.
As to the causes, declining competitive pressures appear to have contributed to a slower flow of investment and capital from low- to high-productivity firms, and potentially weighed on aggregate investment. This is consistent with earlier work focusing on labour reallocation (Hambur forthcoming). There is also some tentative evidence that declining competitive pressures have held back aggregate investment, with firm-level average investment declining most in industries with the largest mark-up increases. But we also find evidence that access to debt finance may have played a role in supressing investment activity amongst productive firms. This is not evident when focusing on labour, which is not surprising given investment is more likely to be financed through debt than is labour (e.g. Spaliara 2009). Our finding highlights the benefits of extending the analysis to investment in trying to understand the causes of declining economic dynamism and productivity growth. And finally, simple tests suggest that the slowdown does not reflect increasing use of intangible capital, which is often poorly measured, though we can't rule out the possibility that this has played some role.
The remainder of the paper is structured as follows. First we provide further discussion of the economic context and existing literature. In Section 3 we describe the data before outlining the baseline model and results in Section 4. In Section 5 we dig into the potential causes for the slowdown in capital reallocation. Section 6 attempts to estimate the macroeconomic effects of the slowdown, before Section 7 concludes.
2. Capital Flows, Investment and Productivity
2.1 Declining investment
Investment is a key contributor to growth in output and labour productivity. If the amount of capital workers have to use increases (capital deepening), it will generally enable them to produce more output and so be more productive. While slower growth in MFP has been the key driver of slower labour productivity growth in recent decades (Duretto, Majeed and Hambur 2022), slower capital deepening has also contributed.
More generally, investment was somewhat weaker than expected in Australia in the 2010s (Debelle 2017; Heads of Treasuries 2017). Despite accommodative monetary policy, investment remained at low levels, reaching a historically low share of non-mining output (Figure 1).
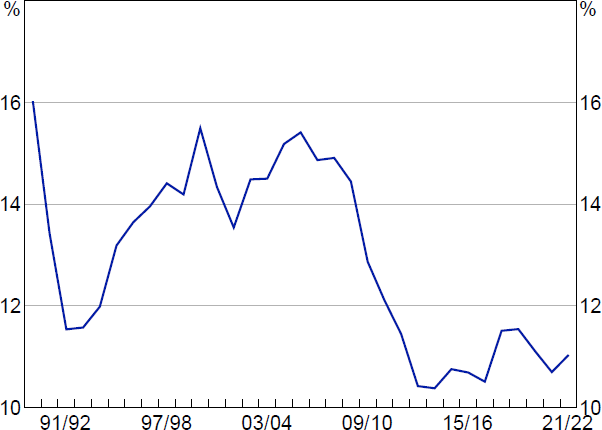
Note: Calculated as private non-mining investment divided by non-mining gross value added.
Sources: ABS; Authors' calculations
Numerous explanations have been put forward to explain the weakness in non-mining investment. Hambur and Jenner (2019) show that the decline reflects broad-based weakness in average investment across firms and industries, rather than any sectoral shift towards less-investment-intensive industries. This is also evident in Figure 2, which shows that non-mining firms' average investment intensity (investment-to-output ratio) declined fairly consistently from 2005 to 2017, even once accounting for compositional changes in firms' age, industry and size (orange line), or firm-specific factors (red line).[3]
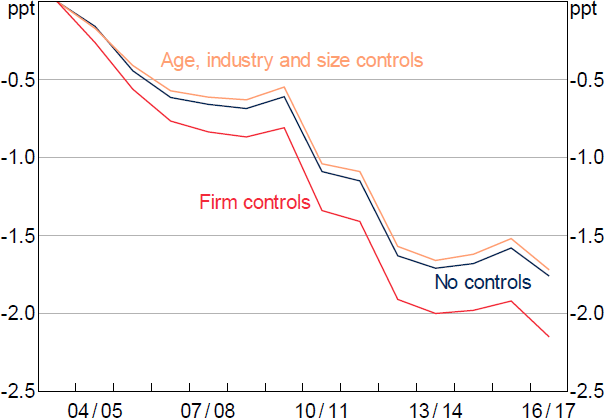
Notes: Regression of firm-level investment on time dummies, and controls as noted. Sample of firms with estimated MFP.
Various other explanations have been put forward in the Australian context: risk aversion and uncertainty; pessimism about future outcomes (‘animal spirits’); sticky hurdle rates; less demand for non-mining investment to support the mining boom; slower depreciation of capital; and lower MFP growth (e.g. van der Merwe et al 2018; Hambur and Jenner 2019; Edwards and Lane 2021).
Similar declines in investment have been documented overseas (e.g. Chen et al 2019). Guttiérez and Philippon (2016) test numerous explanations in the US context, including: financing frictions; the rise of intangibles; globalisation; declining competitive pressures; regulatory barriers; and short-termism. They find evidence that a combination of factors likely weighed on US investment, including intangibles use, short-termism and declining competition.
2.2 Declining dynamism
Numerous studies have documented a slowdown in business and economic dynamism both in Australia (Deutscher 2019; Andrews and Hansell 2021; Andrews et al 2022) and overseas (e.g. Calvino, Criscuolo and Verlhac 2020). This has included evidence of: slower adoption of new frontier technologies (Andrews, Criscuolo and Gal 2019; Akcigit and Ates 2019); declining firm entry rates (Gutiérrez and Philippon 2019); and a slowdown in the efficiency of resource reallocation (Decker et al 2020).
Particularly relevant to this paper, Andrews and Hansell (2021) show that the rate at which labour has flowed from less to more productive firms (within an industry) has slowed. This suggests that labour may not be being allocated as efficiently, and the authors show that the weakening link between firm employment growth and firm productivity can account for around a quarter of the slowdown in aggregate labour productivity observed in recent decades. In turn, Hambur (forthcoming) shows that the link between employment growth and productivity weakened more in industries with growing mark-ups, suggesting a role for declining competitive pressures.
2.3 Capital allocation
Several of the potential explanations for slower investment growth and economic dynamism overlap. For example, financial frictions that prevent investment may also prevent firms from expanding and therefore slow labour reallocation. Similarly, declining competitive pressures that blunt firms' incentives to improve and expand, or exit, might also affect their incentives to invest. More generally, if more productive firms become slower to expand their stock of labour they may also be slower to invest and expand their capital stock.
This raises the question, is there a common driver of declining dynamism and slower investment in Australia? And could the economic effects of weak investment be compounded by it being allocated less efficiently?
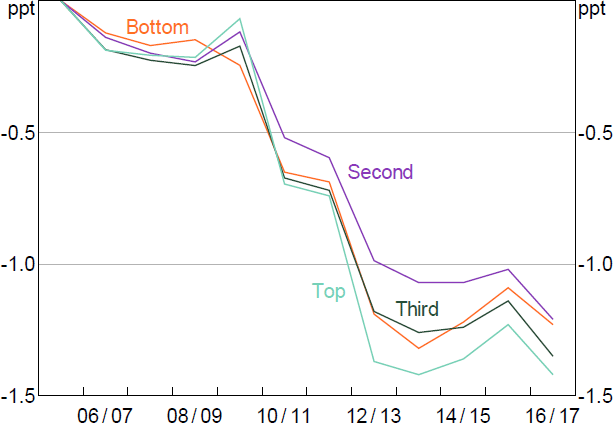
As a simple first step, Figure 3 reproduces the orange line in Figure 2 that showed the average decline in firm investment intensity, but shows it separately for firms in each quartile of the (within-industry) productivity distribution. The declines in investment intensity have generally been larger for firms outside the lowest MFP quartile. So not only is aggregate investment falling, proportionately more of it is being done by the least productive firms. This provides some evidence that declining dynamism and investment may be linked and caused by similar factors.
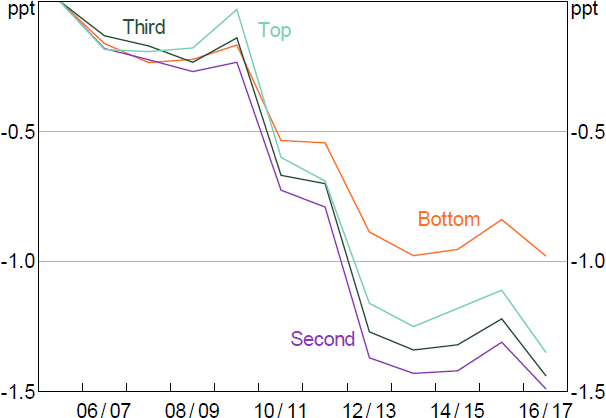
Notes: Regression of firm-level investment on time dummies, and industry size and age controls. Sample of firms with estimated MFP.
To explore these results more formally, as well as considering their drivers and implications, we turn to a regression framework in Sections 4, 5 and 6.
3. Data
The analysis in this paper exploits firm-level data from the Business Longitudinal Analysis Data Environment (BLADE), compiled by the Australian Bureau of Statistics. BLADE consists of administrative data from the Australian Taxation Office (ATO) on the near universe of firms matched with ABS survey microdata, such as the Business Characteristics Survey.
The particular data we use come from firms' business income tax forms and pay as you go (PAYG) employment forms. The former contain data on firms' sales, income and expenses, and balance sheet. These are used to construct measures of firm output, inputs and capital stocks. The PAYG statements are used to derive a measure of full-time equivalent (FTE) employment (Hansell, Nguyen and Soriano 2015), which we use as labour inputs.
For most of the analysis, our measure of capital is defined as (deflated) non-current assets. As discussed below, we also construct a measure of the capital stock using a perpetual inventory method (PIM), which uses information on the firm's investment, depreciation and asset sales to build an estimate of the capital stock (see Appendix A).
Our main measure of productivity is MFP, as this is the more theoretically appropriate metric (Decker et al 2020). MFP is obtained by estimating a translog, gross output production function, using the proxy approach in Ackerberg, Caves and Frazer (2015). For more details see Hambur (forthcoming). We also construct simple measures of labour productivity (ratio of value-added to FTE) and capital productivity (ratio of value-added to capital stock), for extensions and robustness.
All production function inputs are deflated using division-level deflators rather than firm-level prices. While not ideal, this is very common in the literature as firm-level prices are not readily available in most datasets. Moreover, several papers have demonstrated that measures of productivity deflated using industry- and firm-level deflators tend to be very similar, and lead to similar results in regressions such as those undertaken in this paper (Foster, Haltiwanger and Syverson 2008; Decker et al 2020; Blackwood et al 2021).[4]
While BLADE contains the (near) universe of Australian firms, we have to make some exclusions. We focus on the non-financial market sector, as is common in the literature, given the difficulty measuring capital and outputs in the finance sector and complexities around the role of government in the public sector. We focus on employing firms, given the need for non-zero labour inputs in productivity estimation. And we remove sole trader organisations, given these organisations do not report on their balance sheets in the tax data, as well as very young firms given we need a few years of data to estimate MFP (though these are included in some extensions using capital productivity). We include the primary sector (agriculture and mining) in our analysis, but show that the results are robust to its exclusion.
Even with these exclusions we capture a very large proportion of the non-finance market sector: on average we cover about 60 per cent of the sales in each constituent industry division (see Hambur (forthcoming)). As such the dataset remains large and highly representative, though it will be slightly skewed towards older and larger firms compared to Andrews and Hansell (2021).
4. Has Capital Reallocation Slowed?
4.1 Empirical framework
To investigate whether the link between firm capital growth and productivity has changed, we apply the model outlined by Decker et al (2020) for estimating the responsiveness of firm growth (employment or capital) to productivity. Their approach is motivated by canonical models of firm dynamics, which predict that conditional on initial size, more productive firms should grow more quickly than less productive firms.
In particular, Decker et al (2020) show that for a broad range of models with a decreasing returns to scale revenue function due to decreasing returns to scale production or inelastic demand:
employment growth will be increasing in the level of productivity (MFPi,t), conditional on initial firm size Ei,t−1 (which captures past productivity as well as other past factors influencing employment):
Taking a simple first-order log-linear approximation yields:
The coefficient captures how responsive employment growth will be to productivity. This will be affected by a number of factors, including any costs in adjusting the firm's labour (see Section 5).
As in Decker et al (2020), this same model can be extended to capital and investment. As such, the basic set-up of our regression model is:
where future growth is a function of current log productivity (MFP) of firm i at time t, expressed as a deviation from the industry average. This means that we are abstracting from differences in productivity levels across sectors, and focusing on high- versus low-productivity firms as defined within industries. Finally, the vector X includes controls for initial firm size and age (a dummy for young firms below five years old), past firm sales growth, industry-by-time fixed effects, and the (demeaned) state unemployment rates alone and interacted with productivity.
Our measure of capital growth is defined as the change in the capital stock divided by the average capital stock across both periods following Davis, Haltiwanger and Schuh (1996):
where Ki,t is the capital stock of firm i in period t. This measure is bounded between −2 and 2 and it is a second-order approximation of the log difference for growth rates around zero. Further it can accommodate growth of entering and exiting firms, in which case the function takes a value of 2 (entry; Kt = 0) or −2 (exit; Kt+1 = 0). However, for our purposes we focus on the intensive margin and abstract from entry and exit given Andrews and Hansell (2021) already explored the exit margin.[5]
Since our aim is to identify how productivity-enhancing reallocation is evolving in a structural sense, the model controls for cyclical influences in three key ways. First, we control for time-varying shocks at a four-digit ANZSIC 2006 level (the finest possible level of industry classification). This will capture any shocks hitting the industry that might influence investment and firm performance overall. Second, the inclusion of the state unemployment rate directly controls for state-level business cycles. And finally, by interacting state-level unemployment with productivity we control for any cyclicality in the responsiveness of capital growth to firm productivity.[6]
Across all versions of the baseline model we are interested in the sign and significance of the coefficient on productivity, . If positive and significant, we can infer that capital flows to more productive firms at the expense of less productive firms within industries, indicating that the process of capital reallocation is productivity enhancing, even after controlling for a range of cyclical influences.
We can then extend this model to allow the coefficient on productivity to vary across periods. In particular, we examine whether the coefficient changes during the global financial crisis (GFC) (2007/08 to 2010/11), and post-GFC (2011/12 to 2016/17).
This is not the only approach to considering static and dynamic allocative efficiency. Hsieh and Klenow (2009) use the dispersion in measured revenue-based MFP, assuming that any dispersion indicates a misallocation of resources. However, recent research argues that this only holds under a fairly restrictive set of assumptions that equalise marginal quantity-based MFP and average revenue-based MFP. If the assumptions do not hold, the measured dispersion reflects noise, as well as any true misallocation (Haltiwanger, Kulick and Syverson 2018). Other approaches, such as Baqaee and Fahri (2020), take a more structural approach. However, we follow the approach of Decker et al (2020) given its parsimony, transparency and robustness, and to be consistent with previous analysis.
4.2 Baseline results
Table 1 shows the results from the baseline model. As evident in columns 1 and 2, the coefficient on productivity is positive, indicating that more productive firms tend to grow their capital stocks more quickly, meaning capital appears to flow from less to more productive firms (as a share of total capital). However, as evident in column 2, the speed of the reallocation seems to have slowed in the most recent period.
| Non-current assets | Non-current assets | FTE | |
|---|---|---|---|
| Productivity | 0.022*** (0.004) |
0.036*** (0.007) |
0.179*** (0.013) |
| GFC*Productivity | −0.001 (0.008) |
−0.065*** (0.007) |
|
| Post-GFC*Productivity | −0.024*** (0.008) |
−0.093*** (0.007) |
|
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Size | Y | Y | Y |
| Age | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,048,427 | 2,048,427 | 2,048,427 |
| Adj R-squared | 0.031 | 0.031 | 0.050 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
|||
To provide some sense of the magnitude, pre-GFC the model implies that a more productive firm (one standard deviation above the industry mean) would grow its capital stock around 7.2 percentage points faster than a low-productivity firm (one standard deviation below the mean). However, this gap fell to 2.4 percentage points, or by around two-thirds.
To get a sense of whether labour or capital reallocation has slowed by more, we re-run the model looking at growth in employment. The results in column 3 show that the rate of productivity-enhancing labour reallocation has declined by a slightly smaller amount, approximately halving over the period. So the relationship between capital growth and productivity has weakened slightly more than employment and productivity, though the two do not differ substantially.
We also run the baseline model in column 2 of Table 1 but replacing MFP with an indicator capturing where in the industry productivity distribution the firm sat in year t (by quartile). This allows for a more flexible, non-parametric treatment that could be more robust than the linear relationship assumed above. Figure 4 shows the result. We see that over time the gap in capital growth between the least productive firms and other firms has narrowed, particularly for the most productive quartile.
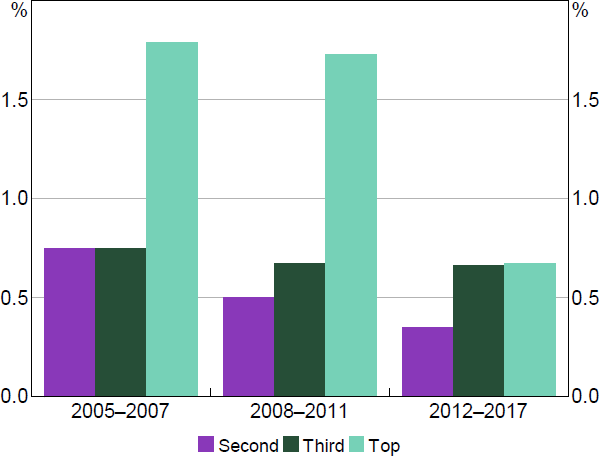
Note: Based on bounded capital growth rate.
One interpretation is that Australian capital accumulation over the course of the productivity slowdown can be characterised as ‘doing less, with less’: not only are firms doing less investment, but the investment that is undertaken is likely lower yielding. This raises the prospect that there is an allocative dimension to the business investment slowdown and that the frictions impeding Australian economic dynamism have infected capital deepening as well as MFP.
We consider five further robustness checks. First, we consider the possibility that measurement error or similar issues could introduce endogeneity, given the capital stock enters the production function, and so is used to estimate (lagged) MFP, but it also enters capital growth (division bias). For example, if a firm re-valued an asset, this could flow through to measured investment and MFP. To account for this we try two different capital growth measures (while continuing to use our baseline capital stock measure in the MFP estimation). The first is a PIM-based capital stock measure. The second is gross investment, scaled by lagged total capital. The use of gross investment also links the analysis more directly to the observed slowdown in aggregate investment.[7] As shown in Table B1, the results are similar using these metrics.
Second, we remove the primary sector, agriculture and mining, to ensure it is not driving the results. Measurement of investment and the capital stock in this sector could be subject to greater mismeasurement due to the important role of land in production, while the mining boom may also affect outcomes. The results are robust to removing the primary sector (Table B2).[8]
The third robustness test is to consider whether the dynamic nature of investment could affect our results. Investments could take place over multiple years, or could be lumpy with firms making large investments one year then very little in the following years (e.g. Bond and Van Reenen 2007; Hambur and La Cava 2018). To account for such dynamics, we extend the regression in Table 1 to include the lagged capital stock or growth, and allow their coefficients to change over time as with productivity, as done in Decker et al (2020). Doing so does not change the results (Table B3).[9] Relatedly, we also consider whether the persistence of productivity shocks may have declined, which could make firms less responsive given the lumpy and irreversible nature of investment. However, there is no substantive evidence of such a change (Table B4).
Fourth, we remove firms that are considered small for tax purposes, below $2 million in turnover, to abstract from changes in tax incentives that may have influenced investment behaviour (Table B5). The results are largely unchanged.
Finally, the translog production function could be a problem. The advantage of a translog over a Cobb-Douglas function is that it allows for the possibility that large firms may have different production technologies to small firms. However, the model may be ‘overfitting’, potentially making large high-productivity firms look less productive (for example). As such, we also run the baseline model using MFP estimates from a Cobb-Douglas production function and find similar results (Table B6).
To get some initial indications of why the relationship between productivity and capital growth weakened, we re-estimate the model over sub-samples of young and older firms (above or below five years old). To do so we use a simpler measure of (log) capital productivity, as MFP estimation requires several years of data, meaning that the sample of young firms for whom we have MFP estimates is relatively small.
The results are shown in Table 2. The first thing to note is that the relationship between productivity and capital growth appears stronger for young firms, consistent with these firms being in an ‘up or out’ stage of their development, where they are experimenting and succeeding, or failing and exiting. The second thing to note is that the weakening of the relationship between productivity and capital growth is more notable for older firms. This suggest that the slowdown in reallocation does not simply reflect a compositional shift towards older firms in the economy as entry rates have fallen, though that will have contributed. Rather the slowdown appears to be ‘within’ both older incumbent and younger firms. This finding is robust to using MFP, though the sample of young firms decreases substantially (Table B7).
| Young | Old | |
|---|---|---|
| Productivity | 0.123*** (0.003) |
0.064*** (0.002) |
| GFC*Productivity | −0.003 (0.002) |
−0.004*** (0.001) |
| Post-GFC*Productivity | −0.011*** (0.003) |
−0.019*** (0.001) |
| Controls | ||
| Industry*Year | Y | Y |
| State*Year | Y | Y |
| State unemp*Productivity | Y | Y |
| Age | Y | Y |
| Size | Y | Y |
| Sales growth | N | N |
| Observations | 460,740 | 2,143,518 |
| Adj R-squared | 0.115 | 0.038 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. ‘Young’ is firms 0-5 years of age, ‘Old’ over 5 years of age. Lagged sales growth variable removed to increase sample of small firms. |
||
5. Understanding the Slowdown
There is strong evidence that productivity-enhancing reallocation of capital within industries has slowed. A key question from a policymaker's standpoint is why? This can inform any potential policy response and can also indicate whether the slowdown is likely to be temporary or ongoing.
To help think about potential drivers, it is useful to return to the model outlined in Decker et al (2020) that the regression framework is based on. The model points to three factors that could account for a weakening in the relationship between firm capital growth and productivity:[10]
- Increases in ‘Correlated wedges’ that distort decisions for more productive firms, causing them to grow (or appear to grow) more slowly.
- Increases in ‘Frictions’ that make it more costly for firms to adjust their labour or capital inputs.
- Declines in ‘Revenue returns to scale’, either due to decreases in returns to scale in production or demand becoming more inelastic, that make the gain from increasing inputs smaller.
We explore three potential explanations that map to these changes, the first of which is more benign, and the latter two which are more concerning.
- The increasing importance of intangible and digital capital, particularly for more productive firms, which could act like a correlated wedge, lowering measured investment for more productive firms.
- Financing constraints becoming more binding, which represents an increase in frictions.
- Declining competition, which equates to a more inelastic demand curve and so a decline in revenue returns to scale.
We choose these three explanations due to their prominence and importance in other papers, though note that there are many other potential avenues that could be explored in future work.[11]
5.1 Intangible and digital capital
One potential explanation for the apparent weakening in the relationship between capital growth and productivity could be the increasing use of intangible and digital capital. Numerous papers have highlighted the increasing importance of digital and other forms of intangible capital (e.g. advertising and goodwill) in firms' production processes over recent decades (e.g. Haskell and Westlake 2017). However, these types of capital are often not well-measured in firm-level data. For example, while the BLADE tax data on assets do capture certain types of intangible capital (e.g. the value of patents), other types, such as accumulated brand value gained through advertising, are not generally captured. Similarly, some digital capital such as software tends to be recorded as an expense, rather than as capital.
As such, one potential explanation for the results could be that highly productive firms are increasingly investing in intangible and digital capital, rather than physical capital. As this is not captured in our capital growth measure this could make it look like the relationship is weakening, even if it is not.[12] That said, the bias could also flow the other way if low-productivity firms are ‘catching-up’ and increasingly investing in intangibles as their importance becomes more widespread throughout the economy (rather than just being used by the most productive firms).
Testing for this explanation is inherently difficult, as intangible capital investment is not well measured. As a simple approach, we examine whether the slowdown has been more evident in sectors that tend to use digital or intangible capital more intensively. If we think that more productive firms have increasingly turned to intangible and digital capital, and that this is driving the results, we may expect to see the slowdown in productivity-enhancing capital reallocation be larger in sectors which can and do tend to make more use of such capital. Put another way, we might expect the bias to be worse in sectors where there is a lot of incentive and scope for the high productivity firms to use intangibles.
We use the measures of digital intensity from Calvino et al (2018) based on cross-country data, and of intangible intensity from Demmou, Stefanescu and Arquie (2019) based on US data. We split industries into the most intensive quartile, and other industries, and re-run the model over these sub-samples.
Consistent with the idea that intangible or digital capital use can lead to measurement issues, we see no relationship between productivity and capital growth in the most intensive sectors (Table 3). This is similar to Decker et al (2020), who find no significant relationship between productivity and capital growth in high-tech sectors in the 2000s. More importantly though, the weakening of the relationship is driven by other sectors. This provides some evidence that the results are not driven by increased use of mis-measured intangible and digital capital, though we cannot rule out that this plays some role.[13]
| Most digitally intense quartile | Other digital intensities | Most intangible intense quartile | Other intangible intensities | |
|---|---|---|---|---|
| Productivity | 0.005 (0.010) |
0.047*** (0.010) |
−0.001 (0.010) |
0.047*** (0.009) |
| GFC*Productivity | 0.013 (0.014) |
−0.007 (0.009) |
0.016 (0.014) |
−0.008 (0.010) |
| Post-GFC*Productivity | −0.010 (0.013) |
−0.029*** (0.009) |
−0.008 (0.013) |
−0.025** (0.010) |
| Controls | ||||
| Industry*Year | Y | Y | Y | Y |
| State*Year | Y | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y | Y |
| Size | Y | Y | Y | Y |
| Age | Y | Y | Y | Y |
| Sales growth | Y | Y | Y | Y |
| Observations | 456,544 | 1,631,670 | 417,597 | 1,431,538 |
| Adj R-squared | 0.031 | 0.029 | 0.030 | 0.030 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
||||
5.2 Financial constraints and credit supply
Firms have to fund investment, either through internally generated cash flows or via external debt or equity finance. Another potential explanation for the slower flow of capital to more productive firms could be that it has become more difficult for firms to obtain external funding, increasing frictions in investing. This could, for example, reflect declining credit supply, or increasing financial frictions due to firms having less collateral or greater information asymmetries. For example, changing views around risks and regulatory changes following the GFC could, in theory, have tightened firm financing constraints (though Australia was less directly affected by the crisis).
There is a large literature examining the effects of financing frictions and credit availability on firm investment and growth (e.g. Rajan and Zingales 1998). This literature measures financial frictions and credit supply in numerous ways, and there is no one agreed upon ‘best’ measure.
We take two relatively simple approaches from the literature to try to identify groups of firms who may be more exposed to changes in financial frictions and credit supply, to try to tease out the role of financing availability. First, we construct some simple firm-level measures of financial fragility. Second we use industry-level measures of external finance dependence.
5.2.1 Firm-level dependence
We consider two measures that could make firms more exposed to a decline in the availability of external funding:
- Gearing, measured as non-current liabilities as a share of assets. Highly geared firms may have more trouble raising additional external finance to fund future investment.
- Negative cash flows, measured as having negative earnings before interest and depreciation. These firms will not be generating internal cash flows, and so will need to fund investment via external funding.
Table 4, columns 1 and 2 show the results for gearing, where we define highly geared as gearing above the median in the industry in the year. The weakening in the relationship is evident mainly for the less-geared firms. Results are similar if we define high gearing using the top quartile or decile.[14]
The results are similar if we look at cash flow (columns 3 and 4). Cash flow negative firms have a much weaker relationship between productivity and capital growth, suggesting they are constrained. But the weakening in the relationship has mainly occurred for the cash flow positive firms.
| High gear | Low gear | Cash flow positive | Cash flow negative | |
|---|---|---|---|---|
| Productivity | 0.030*** (0.011) |
0.031*** (0.009) |
0.037*** (0.007) |
0.001 (0.018) |
| Post-GFC*Productivity | −0.015 (0.012) |
−0.028*** (0.010) |
−0.028*** (0.007) |
0.002 (0.023) |
| Controls | ||||
| Industry*Year | Y | Y | Y | Y |
| State*Year | Y | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y | Y |
| Age | Y | Y | Y | Y |
| Size | Y | Y | Y | Y |
| Sales growth | Y | Y | Y | Y |
| Observations | 797,238 | 1,252,029 | 1,724,572 | 324,695 |
| Adj R-squared | 0.031 | 0.028 | 0.033 | 0.023 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. Gearing is two periods lagged to ensure assets not used in both capital growth and gearing in same period. Cash flow is lagged cash flow. Results robust to contemporaneous. |
||||
This provides some evidence that increasing financing frictions and decreasing credit supply do not account for the slowdown in capital reallocation. However, there are a number of concerns with these firm-based metrics. First, firms may appear highly geared, or have negative cash flow, as they are in a growth phase and this could complicate the interpretation (though the inclusion of the age variable may assist here). Second, just because the other firms are not financially fragile based on these metrics does not mean that they have not been affected by increases in financing frictions. For example, a cash flow positive firm with large financing needs would still be affected by a decline in credit supply. And finally, it might be that we are actually capturing firms that are distressed and unable to invest whether or not financial conditions worsen (e.g. La Cava 2005). This is consistent with the lack of relationship between productivity and investment for cash flow negative firms. As such, we turn to industry-based metrics.
5.2.2 Industry-level dependence
To abstract from the above concerns, and incorporate a broader sense of firms' potential funding needs, we consider some industry-level measures of external finance dependence. If credit and financing frictions have contributed to slower reallocation, we might expect to see a more substantial slowdown in industries that make more use of external finance.
To consider this we use industry-level measures of external finance constructed by Demmou et al (2019). These measures are constructed using the approach pioneered in Rajan and Zingales (1998), and measure the external financing need as the gap between average investment and internally generated cash flows for the industry. Demmou et al construct these measures using US COMPUSTAT data.
Using US-based metrics has some advantages and some disadvantages. The obvious disadvantage is that industries may finance themselves differently in Australia and the United States. Still, there are a number of advantages: using an external dataset limits potential endogeneity concerns; the US data are based on a much longer sample than we have available; the US-based metrics are well-documented and have been used in numerous different studies, making them a robust and comparable set of indicators.
Demmou et al (2019) produce these measures on an ISIC Revision 4 basis, and we map them to ANZSIC 4-digit industries. We allocate industries as being amongst the top quartile of most exposed firms, or being in other quartiles.
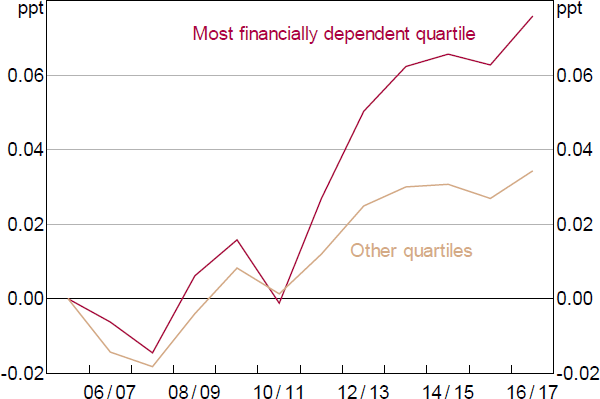
We see that the slowdown has been somewhat larger and more significant in the most financially dependent sectors (Table 5, columns 1 and 2). We see similar results using measures of financial dependence that also account for investment in intangibles and R&D (Table B8), providing further evidence that the results are not simply driven by sectors that may be increasingly investing in (unmeasured) intangibles. The results are also robust to removing mining and agriculture (Table B2) or large firms.[15] In this case, though, the results are less robust to using the capital productivity measure.
| Most financially dependent quartile | Other financial dependence | Most equity dependent quartile | Other equity dependence | |
|---|---|---|---|---|
| Productivity | 0.052*** (0.016) |
0.026*** (0.009) |
0.011 (0.010) |
0.050*** (0.010) |
| GFC*Productivity | −0.016 (0.017) |
−0.006 (0.009) |
0.011 (0.013) |
−0.009 (0.013) |
| Post-GFC*Productivity | −0.044*** (0.014) |
−0.010 (0.009) |
−0.015 (0.012) |
−0.025** (0.011) |
| Controls | ||||
| Industry*Year | Y | Y | Y | Y |
| State*Year | Y | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y | Y |
| Size | Y | Y | Y | Y |
| Age | Y | Y | Y | Y |
| Sales growth | Y | Y | Y | Y |
| Observations | 559,635 | 1,327,664 | 581,262 | 1,306,037 |
| Adj R-squared | 0.033 | 0.031 | 0.032 | 0.031 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
||||
Interestingly, the same pattern is not observed if we consider external equity dependence, with the slowdown being evident in the less equity dependent sectors (columns 3 and 4). The relationship between investment and productivity is much weaker in sectors with high equity dependence, potentially indicating lesser availability of equity finance in the first place and greater financing frictions. However, the slowdown is more visible in the less equity finance dependent sectors. Taken together, this suggests that the slowdown relates to a tightening in access to debt finance.
Notably, if we consider employment growth, rather than capital growth, reallocation slowed similarly in sectors with both high and lower external finance dependence (Table 6). In this case both the initial relationship between employment growth and productivity, and the change in the relationship, are broadly similar. This finding is robust to using labour productivity, rather than MFP. Given financing frictions are more likely to impinge directly on investment this is not surprising (e.g. Spaliara 2009), and highlights the value in exploring capital reallocation to better understand the factors weighing on business dynamism and productivity growth.[16]
Overall, the results indicate that those sectors that tend to rely most heavily on debt finance experienced the greatest slowdown in capital reallocation, with the gap in outcomes between high-and low-productivity firms falling the most. This provides some evidence that financing constraints may have become more binding over this period, preventing high-productivity firms from investing.
| MFP | Labour productivity | ||||
|---|---|---|---|---|---|
| Most financially dependent quartile | Other financial dependence | Most financially dependent quartile | Other financial dependence | ||
| Productivity | 0.173*** (0.025) |
0.188*** (0.016) |
0.051*** (0.004) |
0.053*** (0.015) |
|
| GFC*Productivity | −0.052*** (0.011) |
−0.071*** (0.009) |
−0.010*** (0.002) |
−0.011*** (0.013) |
|
| Post-GFC*Productivity | −0.074*** (0.014) |
−0.107*** (0.009) |
−0.009*** (0.002) |
−0.014*** (0.002) |
|
| Controls | |||||
| Industry*Year | Y | Y | Y | Y | |
| State*Year | Y | Y | Y | Y | |
| State unemp*Productivity | Y | Y | Y | Y | |
| Size | Y | Y | Y | Y | |
| Age | Y | Y | Y | Y | |
| Sales growth | Y | Y | Y | Y | |
| Observations | 559,635 | 1,327,664 | 630,552 | 1,501,646 | |
| Adj R-squared | 0.052 | 0.050 | 0.058 | 0.059 | |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
|||||
It is unclear whether the results would be stronger or weaker if we were able to include very young firms. On the one hand, they may be stronger as young firms tend to be more sensitive to financial constraints, given they are growing and may have volatile cash flows which can make it hard to finance investment internally. On the other hand, if young firms are always subject to constraints, and the change largely reflects constraints becoming more binding for older firms, including younger firms may actually weaken the results.
5.3 Competition
One final explanation we explore is declining competition. As also discussed in other papers (e.g. De Loecker, Eeckhout and Unger 2020), decreases in competitive pressure can limit selection effects, meaning that unproductive firms may be less likely to shrink and exit, freeing up resources for higher productivity firms. At the same time, more productive firms may have less impetus to continue to grow and improve to stay ahead of their competitors. More generally, in many models where market power is higher, production, and therefore input use, will be less responsive to productivity shocks. As such, the relationship between productivity, and capital growth and reallocation, may be weaker.[17]
To examine this, we estimate the following extension to the earlier model:
where is the industry-level unweighted average mark-up from Hambur (forthcoming). In running these regressions we de-mean industry mark-ups. This controls for the possibility that there may be some third time-invariant factor that affects both the level of industry mark-ups, and the strength of the reallocation effects. It also means we are focusing on the effect of changes in mark-ups (from the industry average), limiting concerns about issues in identifying the levels of mark-ups.[18]
Table 7 shows the results for capital growth, alongside employment growth similar to Hambur (forthcoming). Where mark-ups and market power increase, the relationship between productivity and capital reallocation weakens, as with employment growth. For example, taking the national average increase in mark-ups of around 5 percentage points and applying it to the coefficients, the relationship weakened by half over the sample. In relative terms, the effect of markups on capital growth appears slightly larger than the effect on employment growth.
| Capital growth | Gross investment | Employment growth | |
|---|---|---|---|
| Productivity | 0.020*** (0.004) |
0.076*** (0.003) |
0.108*** (0.008) |
| Mark-up*Productivity | −0.199*** (0.065) |
−0.146*** (0.045) |
−0.319*** (0.064) |
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Size | Y | Y | Y |
| Industry*Productivity | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,049,267 | 2,049,267 | 2,049,267 |
| Adj R-squared | 0.029 | 0.024 | 0.049 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. Overall sample is 2004/05 to 2016/17. Unweighted average industry mark-ups, demeaned. Gross investment scaled by lagged capital stock. |
|||
Rising mark-ups also appear to weaken the relationship between gross investment and firm productivity (column 2). Given this link, it's also worth exploring whether there is any evidence that rising mark-ups were associated with lower aggregate investment. As a simple approach, we revisit Figure 3, but instead of separating firms based on their productivity quartile, we separate them based on whether their industry had a large increase in mark-ups over the sample – or more precisely, which quartile their industry fell into in the distribution of industry mark-up changes.
Figure 5 shows the results. While they are less compelling than the productivity grouping results, there is evidence that investment declined most in the industries that experienced the largest increase in mark-ups. This provides some evidence that increasing mark-ups and declining competitive pressures may have contributed to weakness in aggregate investment. And more generally, it provides further evidence that the factors that are driving slowing dynamism and reallocation are also contributing to slower aggregate investment.
Finally, it is worth highlighting that the competition and financial constraints explanations are not necessarily independent. For example, while declining competitive pressures might reflect weaker enforcement by regulators, it could also reflect other barriers that prevent firms entering, growing and competing, like financing constraints. We find some evidence that the two causes could be linked, as the increases in mark-ups were on average larger in the most financially dependent industries (Figure B1). But further work is required to better understand the ultimate causes of declining competition and dynamism.
Notes: Regression of firm-level investment on time dummies, and industry, size and age controls. Sample of firms with estimated MFP. Quartiles defined based on industry change in mark-ups over sample 04/05 to 16/17.
6. Aggregate Implications
The above results suggest that the relationship between capital growth and productivity has weakened, and that the flow of capital towards more productive firms has slowed. This is likely to have contributed to slower aggregate productivity and output growth as inputs are allocated less efficiently. But by how much?
To answer this, we use an approach similar to Andrews and Hansell (2021) and Hambur (forthcoming), and initially proposed in Decker et al (2020). The basic idea of the approach is to construct a counterfactual productivity index of what would have happened had the relationship between growth and productivity not weakened. In such a case, more productive firms would have been bigger, and so aggregate productivity would have been higher. We can compare the index to actual outcomes, to get a sense of the lost productivity and income.
More precisely, we create indices of aggregate labour productivity that combine actual realisations of firm-level MFP with input shares predicted from an estimated model.[19] The idea is that by varying the strength of the relationship between input growth and productivity, and therefore growth in inputs for different firms, we can construct counterfactual productivity indices that allow us to understand how aggregate productivity would have evolved had reallocation not slowed.
This approach is similar to the one taken in both Andrews and Hansell (2021) and Hambur (forthcoming). However, they focus solely on labour reallocation. Instead, we focus on both labour and capital. The advantage is that by using both inputs, alongside the estimated production functions, we can construct aggregate input indices for the firm, similar to Adelet McGowan, Andrews and Millot (2018). By combining these aggregate input indices with our MFP estimates we can consider what would have happed to aggregate income in the economy, not just labour productivity.
It is important to note that this approach isolates one, very direct channel through which slower reallocation of resources to high-productivity firms could have weighed on aggregate growth: through lower aggregate MFP. It abstracts from any effects slower reallocation of capital could have on the aggregate size of the capital stock, which, based on Figures 3 and 5, could be substantial. It also abstracts from any indirect effects the decline in dynamism could have on firm-level productivity, as examined in Andrews et al (2022).
We consider two different models: i) where the responsiveness of employment and capital growth to (lagged) productivity is allowed to decline; and ii) where the responsiveness is held constant at the level estimated at the start of the sample. These models give different predictions for employment and capital growth in time t+1. We can then combine these predictions with the (initial) level of employment and capital for the firm in t to get predicted inputs.
With these predictions in hand, we can construct three different productivity indices: one using observed input shares in the previous year (Equation (7)); one using the using the shares where the reallocation is allowed to vary (Equation (8)); and one using the share from the model where reallocation is held steady (Equation (9)). More formally:
The difference between the base index and either of the other indices shows the predicted productivity growth due to changes in the strength of reallocation. For example, the predicted gains in productivity based on the model with varying reallocation is:
The difference in these differences then captures how much slower aggregate productivity growth will be due to slower reallocation:
Given we are constructing a counterfactual for MFP, the results can also be thought of as a counterfactual for output growth, due to one-to-one relationship in simple production functions.[20]
Figure 6 shows the results from this exercise. Looking through the volatility, if the relationship between growth and productivity had not weakened, and therefore more productive firms had tended to be larger, aggregate MFP and output growth would have been moderately stronger in each year since 2008. Accumulating this lost growth over the entire period, aggregate real output would have been around 0.75 per cent higher by 2017. This equates to output being around $13 billion lower than it would have been otherwise, and incomes being around $550 lower per capita or $1,000 per worker (in 2017 dollars).
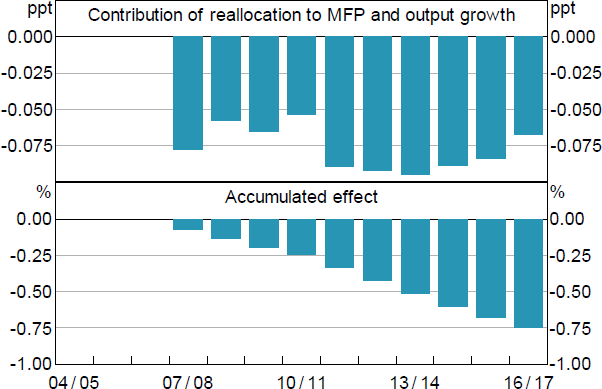
Notes: Based on coefficient in Table 1, column 2. Excludes mining, agriculture and utilities.
To give some sense of how this fits in with the overall slowdown in productivity over this period, Andrews and Hansell (2021) found that slower labour reallocation lowered labour productivity growth by around 0.15 percentage points per year in the mid-2010s compared to the early 2000s. This equated to around a quarter of the overall slowdown in non-mining non-financial private sector labour productivity over the period.
The decline in labour productivity they identify could reflect two factors: slower aggregate MFP growth due to slower growth for high MFP firms, which we explore in this paper; and slower capital deepening, due to slower reallocation of labour to firms with abundant capital, which we do not. Our work suggests that about half the observed slowdown reflected lower MFP growth.
Overall then, these results suggest that had the relationships between firms' employment growth and productivity and capital growth and productivity not weakened, more productive firms would have been substantially larger. This would have meant that both aggregate productivity and income would have been moderately higher, compared with what actually occurred.
7. Conclusion
Over recent decades non-mining investment in Australia and elsewhere has been weak and economic dynamism has declined. Both of these had negative implications for productivity, and in turn very real implications for wages, growth and the welfare of the Australian people.
Our paper links these two important macroeconomic phenomena and shows that the slowdown in non-mining capital accumulation has an allocative component: not only has investment declined, but the decline has been larger amongst more productive firms. This means that capital has also been allocated less productively. The weaker link between investment and productivity, and slower reallocation of capital towards more productive firms, has weighed on incomes. Accounting only for the very direct effect this would have in lowering aggregate MFP, our estimates suggest that in 2017 GDP was around $13 billion, or $550 per person, lower than it would have been otherwise. And this is on top of any direct effects it may have had in lowering the aggregate capital stock, or indirect effects in lessening firm-level productivity growth.
In terms of what has caused this, we find evidence that increasing market power has played a role, muting incentives for better firms to invest and grow their capital stock. This finding complements earlier work that found declining competition had limited incumbent firms' incentives to reallocate labour to more productive firms (Hambur forthcoming) and to innovate and adopt technologies (Andrews et al 2022). It reinforces the need to understand why competitive pressures may be declining, and whether that reflects competition policy or other frictions that prevent new firms from growing and challenging incumbents.
We also find evidence that the slowdown was worse in more debt-dependent sectors, suggesting that frictions in debt markets contributed to slower reallocation of capital to more productive firms. This is not evident when examining labour reallocation, which highlights the value of examining the allocation of investment.
While we only explore competition and financing frictions, the results are consistent with other frictions in the economy increasing, making firms less responsive to economic conditions and opportunities. More work is required to understand these frictions and potential policy responses, as they appear to be holding down overall productivity growth and living standards in Australia.
Appendix A: Data and Sample Statistics
As discussed in the paper, we use data from the ABS BLADE database. The particular data come from firms' business income tax forms and PAYG employment forms.
Regarding the key variables:
- Gross output: measured as firm income. This will include some income not directly related to production, such as interest. However, for most firms this item is small.
- Labour expense: labour costs plus superannuation expenses.
- Fixed costs: rental and leasing expenses, bad debts, interest, royalties, external labour and contractors.
- Intermediate inputs: total expenses less labour, depreciation and fixed costs.
- Value-added: gross output less intermediate inputs.
- Labour input: FTE derived from PAYG statements, using the methodology laid out in Hansell et al (2015).
- Wage rate: labour expense divided by FTE.
- Capital: book value of non-current assets.
All of these metrics apart from FTE are measured in nominal terms. To construct real measures for the inputs into the production functions, we deflate using division-level output, intermediate input and capital deflators. The wage rate is deflated using the output deflator.
As well as our main capital stock measure, we also construct a PIM. To construct this metric we use the following law of motion:
where is the real PIM stock in time t, It+1 is real investment in t + 1 deflated using the gross fixed capital formation deflator, is depreciation in t + 1 deflated using the previous capital stock deflator, and Dt+1 is disposals in t + 1 deflated using the lagged capital stock deflator.
To use a PIM we require a starting value. Our preferred starting value is the firm's reported capital stock in the first year we observe the firm. We also tried assuming the stock was zero in the previous year, and building the stock based on flows. Both lead to similar results.
The PIM approach is not our preferred approach for two reasons. First, PIM can be sensitive to the starting value, particularly in short samples (though that does not appear to be a substantial issue here). The second is that disposals are reported at the cash value of the sale, not the book value. While some data are available on any taxable gain/loss on the sale, which would allow us to get back to the book value, these are not provided for the entire sample.
As noted, we focus on the market sector, and so exclude the Health, Education, and Public Administration divisions. Government plays a large role in these divisions, and capital reallocation may be heavily influenced by public entities. We also exclude the Finance division, given conceptual difficulties in measuring output in this sector (e.g. La Cava 2019).
We exclude all non-employing firms, given these firms will have undefined (log) labour inputs and costs. We choose to exclude all firms with less than one FTE as is common in the literature, as they introduce a large amount of noise into the estimation of MFP. We exclude all sole proprietors, as they do not report information on their balance sheets, and so on their capital stock. Finally, we exclude industries that have very few firms due to difficulty in estimating production functions with small samples. This mainly affects the Mining and Utilities divisions.
Even with these exclusions, we capture a very large proportion of the non-mining non-finance sector (see Hambur (forthcoming)). That said, our sample is slightly skewed towards larger and older firms, compared to the full population (Table A1).
| Mean | Median | ||
|---|---|---|---|
| Revenue (sales, $'000) | 5,592 | 967 | |
| Age(a) | 12 | 11 | |
| Employment (FTE) | 15.6 | 4.4 | |
| Capital growth (%) | 1.0 | −3.0 | |
| Investment-to-capital ratio (%) | 10.4 | 0.0 | |
| Number of firms | |||
| Young | 17,877 | ||
| Total | 177,166 | ||
|
Notes: ‘Young’ is firms 0–5 years of age. (a) Note age provides a lower bound, given some firms' birthdates are mis-reported as 2001 with the introduction of the GST. Sources: ABS; Authors' calculations |
|||
| Number of employees | Bottom quartile | Second quartile | Third quartile | Top quartile |
|---|---|---|---|---|
| 0–4 | 280,650 | 266,771 | 258,759 | 280,916 |
| 5–19 | 139,539 | 192,336 | 210,658 | 171,668 |
| 20–199 | 542,86 | 58,193 | 57,925 | 50,917 |
| 199–500 | 4,664 | 1,765 | 1,361 | 2,363 |
| 500+ | 2,826 | 692 | 581 | 1,934 |
|
Note: Quartiles defined by industry and year. Sources: ABS; Authors' calculations |
||||
Appendix B: Additional Results
| Non-current assets | PIM | Gross investment | |
|---|---|---|---|
| Productivity | 0.036*** (0.007) |
0.060*** (0.007) |
0.085*** (0.005) |
| GFC*Productivity | −0.001 (0.008) |
0.0148* (0.008) |
0.017*** (0.005) |
| Post-GFC*Productivity | −0.024*** (0.008) |
−0.035*** (0.009) |
−0.025*** (0.006) |
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Age | Y | Y | Y |
| Size | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,048,427 | 1,254,739 | 2,048,427 |
| Adj R-squared | 0.031 | 0.020 | 0.024 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. Gross investment expressed relative to lagged non-current assets; winsorised at 99th percentile. |
|||
| All non-primary | Most financially dependent quartile | Other financial dependence | |
|---|---|---|---|
| Productivity | 0.030*** (0.007) |
0.051*** (0.016) |
0.026*** (0.009) |
| GFC*Productivity | 0.008 (0.008) |
−0.012 (0.017) |
0.006 (0.009) |
| Post-GFC*Productivity | −0.022*** (0.008) |
−0.043*** (0.014) |
−0.008 (0.009) |
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Age | Y | Y | Y |
| Size | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 1,900,014 | 550,463 | 1,187,647 |
| Adj R-squared | 0.030 | 0.032 | 0.032 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. Agriculture and mining sectors removed. |
|||
Notes: Regression of industry average mark-ups on time dummies and industry dummies. Primary sector removed. Quartiles defined based on Rajan Zingales financial dependence metric.
Sources: Authors' calculations; Demmou, Stefanescu and Arquie (2019)
| Baseline | With lagged stock | With lagged growth | |
|---|---|---|---|
| Productivity | 0.036*** (0.007) |
0.031*** (0.008) |
0.036*** (0.007) |
| GFC*Productivity | −0.001 (0.008) |
0.002 (0.007) |
0.000 (0.008) |
| Post-GFC*Productivity | −0.024*** (0.008) |
−0.024*** (0.007) |
−0.024*** (0.008) |
| Lagged stock/growth | −0.057*** (0.0016) |
−0.098*** (0.003) |
|
| GFC*Lagged stock/growth | 0.003*** (0.001) |
−0.008** (0.003) |
|
| Post-GFC*Lagged stock/growth | 0.017*** (0.001) |
−0.011*** (0.003) |
|
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Age | Y | Y | Y |
| Size | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,048,427 | 2,048,427 | 2,048,427 |
| Adj R-squared | 0.031 | 0.055 | 0.043 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
|||
| Pre-GFC | GFC | Post-GFC | |
|---|---|---|---|
| Lagged productivity | 0.831*** (0.034) |
0.777*** (0.022) |
0.813*** (0.020) |
| Observations | 501,012 | 645,395 | 1,112,118 |
| Adj R-squared | 0.644 | 0.635 | 0.620 |
| Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and robust to heterogeneity and autocorrelation. Pre-GFC sample is 2004/05 to 2006/07, GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17. | |||
| Full sample | No firms < $2 million sales | Allow firm controls to vary | |
|---|---|---|---|
| Productivity | 0.036*** (0.007) |
0.036** (0.014) |
0.037*** (0.007) |
| GFC*Productivity | −0.001 (0.008) |
−0.002 (0.014) |
0.001 (0.007) |
| Post-GFC*Productivity | −0.024*** (0.008) |
−0.040** (0.017) |
−0.022*** (0.007) |
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Age | Y | Y | Y |
| Size | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,048,427 | 609,735 | 2,048,427 |
| Adj R-squared | 0.031 | 0.045 | 0.031 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. Column 3 allows age, size and sales growth variables' coefficients to change across the periods. |
|||
| Full sample | By period | ||
|---|---|---|---|
| Productivity | 0.021*** (0.003) |
0.030*** (0.007) |
|
| GFC*Productivity | 0.000 (0.008) |
||
| Post-GFC*Productivity | −0.017** (0.008) |
||
| Controls | |||
| Industry*Year | Y | Y | |
| State*Year | Y | Y | |
| State unemp*Productivity | Y | Y | |
| Age | Y | Y | |
| Size | Y | Y | |
| Sales growth | Y | Y | |
| Observations | 1,983,297 | 1,983,297 | |
| Adj R-squared | 0.013 | 0.013 | |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
|||
| Full sample | Young | Old | |
|---|---|---|---|
| Productivity | 0.036*** (0.007) |
0.046** (0.022) |
0.033*** (0.007) |
| GFC*Productivity | −0.001 (0.008) |
−0.009 (0.028) |
−0.002 (0.008) |
| Post-GFC*Productivity | −0.024*** (0.008) |
0.008 (0.027) |
−0.018** (0.008) |
| Controls | |||
| Industry*Year | Y | Y | Y |
| State*Year | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y |
| Age | Y | Y | Y |
| Size | Y | Y | Y |
| Sales growth | Y | Y | Y |
| Observations | 2,048,427 | 230,972 | 1,817,455 |
| Adj R-squared | 0.031 | 0.043 | 0.027 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. ‘Young’ is firms 0–5 years of age, ‘Old’ over 5 years of age. |
|||
| Most financially dependent quartile (with R&D) | Other financial dependence (with R&D) | Most financially dependent quartile (with intangibles) | Other financial dependence (with intangibles) | |
|---|---|---|---|---|
| Productivity | 0.053*** (0.016) |
0.025*** (0.008) |
0.054*** (0.017) |
0.025*** (0.008) |
| GFC*Productivity | −0.019 (0.017) |
0.007 (0.009) |
−0.021 (0.018) |
−0.008 (0.008) |
| Post-GFC*Productivity | −0.041*** (0.015) |
−0.012 (0.009) |
−0.045*** (0.015) |
−0.010 (0.009) |
| Controls | ||||
| Industry*Year | Y | Y | Y | Y |
| State*Year | Y | Y | Y | Y |
| State unemp*Productivity | Y | Y | Y | Y |
| Size | Y | Y | Y | Y |
| Age | Y | Y | Y | Y |
| Sales growth | Y | Y | Y | Y |
| Observations | 481,708 | 1,405,591 | 468,587 | 1,418,712 |
| Adj R-squared | 0.035 | 0.033 | 0.033 | 0.031 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
||||
| Manufacturing | Construction | Wholesale trade | Retail trade | Accommodation | Professional services | Other services | |
|---|---|---|---|---|---|---|---|
| Productivity | 0.039** (0.019) |
0.058** (0.023) |
0.017 (0.022) |
0.029 (0.028) |
0.041** (0.015) |
0.002 (0.010) |
0.057*** (0.018) |
| Post-GFC* Productivity | −0.012 (0.024) |
−0.038* (0.021) |
−0.001 (0.025) |
−0.022 (0.036) |
−0.028 (0.034) |
−0.017 (0.012) |
−0.042 (0.031) |
| Controls | |||||||
| Industry*Year | Y | Y | Y | Y | Y | Y | Y |
| State*Year | Y | Y | Y | Y | Y | Y | Y |
| State unemp* Productivity |
Y | Y | Y | Y | Y | Y | Y |
| Size | Y | Y | Y | Y | Y | Y | Y |
| Age | Y | Y | Y | Y | Y | Y | Y |
| Sales growth | Y | Y | Y | Y | Y | Y | Y |
| Observations | 204,401 | 350,881 | 170,718 | 262,083 | 137,995 | 285,431 | 138,830 |
| Adj R-squared | 0.038 | 0.032 | 0.030 | 0.028 | 0.029 | 0.032 | 0.029 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively. Standard errors are in parentheses and clustered at an industry level. GFC sample is 2007/08 to 2010/11, post-GFC sample is 2011/12 to 2016/17, overall sample is 2004/05 to 2016/17. |
|||||||
References
Ackerberg DA, K Caves and G Frazer (2015), ‘Identification Properties of Recent Production Function Estimators’, Econometrica, 83(6), pp 2411–2451.
Adalet McGowan M, D Andrews and V Millot (2018), ‘The Walking Dead? Zombie Firms and Productivity Performance in OECD Countries’, Economic Policy, 33(96), pp 685–736.
Agarwal R, C Bajada, P Brown, I Moran and A Balaguer (2019), ‘Development of Management Capability Scores’, Australian Government Department of Industry, Innovation and Science, Office of the Chief Economist Research Paper 10/2019.
Akcigit U and ST Ates (2019), ‘What Happened to U.S. Business Dynamism?’, NBER Working Paper No 25756, rev May 2019.
Andrews D, C Criscuolo and PN Gal (2019), ‘The Best versus the Rest: Divergence across Firms during the Global Productivity Slowdown’, Centre for Economic Performance, CEP Discussion Paper No 1645.
Andrews D, J Hambur, D Hansell and A Wheeler (2022), ‘Reaching for the Stars: Australian Firms and the Global Productivity Frontier’, Australian Treasury Working Paper No 2022-01.
Andrews D and D Hansell (2021), ‘Productivity-Enhancing Labour Reallocation in Australia’, Economic Record, 97(317), pp 157–169.l
Baqaee DR and E Fahri (2020), ‘Productivity and Misallocation in General Equilibrium’, The Quarterly Journal of Economics, 135(1), pp 105–163.
Blackwood GJ, LS Foster, CA Grim, J Haltiwanger and Z Wolf (2021), ‘Macro and Micro Dynamics of Productivity: From Devilish Details to Insights’, American Economic Journal: Macroeconomics, 13(3), pp 142–172.
Bond S and J Van Reenen (2007), ‘Microeconometric Models of Investment and Employment’, in JJ Heckman and EE Leamer (eds), Handbook of Econometrics: Volume 6A, Handbooks in Economics 2, North-Holland, Amsterdam, pp 4417–4498.
Calvino F, C Criscuolo, L Marcolin and M Squicciarini (2018), ‘A Taxonomy of Digital Intensive Sectors’, OECD Science, Technology and Industry Working Papers No 2018/14.
Calvino F, C Crisuolo and R Verlhac (2020), ‘Declining Business Dynamism: Structural and Policy Determinants’, OECD Science, Technology and Innovation Policy Papers No 94.
Chen W, F Díez, R Duval, C Jones and C Villegas-Sánchez (2019), ‘The Rise of Corporate Market Power and Its Macroeconomic Implications’, World Economic Outlook: Growth Slowdown, Precarious Recovery, April, IMF, Washington DC, pp 55–76.
Davis SJ, JC Haltiwanger and S Schuh (1996), Job Creation and Destruction, The MIT Press, Cambridge.
De Loecker J, J Eeckhout and G Unger (2020), ‘The Rise of Market Power and the Macroeconomic Implications’, The Quarterly Journal of Economics, 135(2), pp 561–644.
Debelle G (2017), ‘Business Investment in Australia’, Address to the UBS Australasia Conference 2017, Sydney, 13 November.
Decker RA, J Haltiwanger, RS Jarmin and J Miranda (2020), ‘Changing Business Dynamism and Productivity: Shocks versus Responsiveness’, The American Economic Review, 110(12), pp 3952–3990.
Demmou L, I Stefanescu and A Arquie (2019), ‘Productivity Growth and Finance: The Role of Intangible Assets – A Sector Level Analysis’, OECD Economics Department Working Papers No 1547.
Deutscher, N (2019), ‘Job-to-Job Transitions and the Wages of Australian Workers’, Australian Treasury Working Paper No 2019-07.
Duretto Z, O Majeed and J Hambur (2022), ‘Overview: Understanding Productivity in Australia and the Global Slowdown’, Treasury Round Up, October, pp 4–13.
Edwards H and K Lane (2021), ‘Why Are Investment Hurdle Rates so Sticky?’, RBA Bulletin, December.
e61 (2022), ‘Better Harnessing Australia's Talent: Five Facts for the Summit’, e61 Institute Policy Paper.
Foster L, J Haltiwanger and C Syverson (2008), ‘Reallocation, Firm Turnover, and Efficiency: Selection on Productivity or Profitability?’, The American Economic Review, 98(1), pp 394–425.
Gutiérrez G and T Philippon (2016), ‘Investment-Less Growth: An Empirical Investigation’, NBER Working Paper No 22897, rev January 2017.
Gutiérrez G and T Philippon (2019), ‘The Failure of Free Entry’, NBER Working Paper No 26001.
Haltiwanger J, R Kulick and C Syverson (2018), ‘Misallocation Measures: The Distortion That Ate the Residual’, NBER Working Paper No 24199, rev October 2018.
Hambur J (forthcoming), ‘Product Market Competition and Its Implications for the Australian Economy’, Economic Record.
Hambur J and K Jenner (2019), ‘Can Structural Change Account for the Low Level of Non-Mining Investment?’, RBA Bulletin, June.
Hambur J and G La Cava (2018), ‘Do Interest Rates Affect Business Investment? Evidence from Australian Company-Level Data’, RBA Research Discussion Paper No 2018-05.
Hansell, D, T Nguyen and F Soriano (2015), ‘Can We Improve on a Headcount? Estimating Unobserved Labour Input with Individual Wage Data’, Paper presented to the 26th Australian Labour Market Research Workshop, Flinders University, Adelaide, 3–4 December.
Haskell J and S Westlake (2017), Capitalism without Capital: The Rise of the Intangible Economy, Princeton University Press, Princeton.
Heads of Treasuries (2017), ‘Intergovernmental Review of Business Investment’, September.
Hsieh C-T and PJ Klenow (2009), ‘Misallocation and Manufacturing TFP in China and India’, The Quarterly Journal of Economics, 124(4), pp 1403–1448.
Kido Y and Kothari S (2021), ‘Reigniting Productivity Growth in Australia’, in ‘Australia: Selected Issues’, IMF Country Report No 21/256.
La Cava G (2005), ‘Financial Constraints, the User Cost of Capital and Corporate Investment in Australia’, RBA Research Discussion Paper No 2005-12.
La Cava G (2019), ‘The Labour and Capital Shares of Income in Australia’, RBA Bulletin, March.
Productivity Commission (2022), 5-Year Productivity Inquiry: From Learning to Growth, Interim Report No 5, Productivity Commission, Canberra.
Rajan RG and L Zingales (1998), ‘Financial Dependence and Growth’, The American Economic Review, 88(3), pp 559–586.
Spaliara M-E (2009), ‘Do Financial Factors Affect the Capital–Labour Ratio? Evidence from UK Firm-Level Data’, Journal of Banking & Finance, 33(10), pp 1932–1947.
van der Merwe M, L Cockerell, M Chambers and J Jääskelä (2018), ‘Private Non-Mining Investment in Australia’, RBA Bulletin, June.
Copyright and Disclaimer Notice
BLADE Disclaimer
The following Disclaimer Notice refers to data and graphs sourced from the Australian Bureau of Statistics' BLADE (Business Longitudinal Analysis Data Environment) database.
The results of this study are based, in part, on Australian Business Register (ABR) data supplied by the Registrar to the Australian Bureau of Statistics (ABS) under A New Tax System (Australian Business Number) Act 1999 and tax data supplied by the Australian Taxation Office (ATO) to the ABS under the Taxation Administration Act 1953. These require that such data are only used for the purpose of carrying out functions of the ABS. No individual information collected under the Census and Statistics Act 1905 is provided back to the Registrar or ATO for administrative or regulatory purposes. Any discussion of data limitations or weaknesses is in the context of using the data for statistical purposes, and is not related to the ability of the data to support the ABR or ATO's core operational requirements. Legislative requirements to ensure privacy and secrecy of this data have been followed. Only people authorised under the Australian Bureau of Statistics Act 1975 have been allowed to view data about any particular firm in conducting these analyses. In accordance with the Census and Statistics Act 1905, results have been confidentialised to ensure that they are not likely to enable identification of a particular person or organisation.
Acknowledgements
Thank you to Ben Westmore, Omer Majeed, Jarkko Jääskelä, John Simon and seminar participants at the RBA, Australian Treasury and NSW Treasury for their helpful comments. The views expressed in this paper are those of the authors and do not necessarily reflect the views of the Reserve Bank of Australia or e61 Institute. The authors are responsible for any errors.
Footnotes
Economic Research Department, Reserve Bank of Australia [*]
e61 Institute [**]
Other explanations or empirical patterns that have been noted include: slowing diffusion of adoption and technologies (Andrews et al 2022), low levels of R&D (Kido and Kothari 2021), potentially low or mismatched skills and human capital (e.g. Productivity Commission 2022), and low management capabilities (compared to the United States; Agarwal et al (2019)). [1]
While mobility has increased somewhat post-COVID-19, this may reflect a mix of ‘payback’ for low mobility during COVID-19, alongside cyclical strength in the labour market, rather than a structural improvement. [2]
We focus on data up to 2017 to align with the mark-up estimates from Hambur (forthcoming). Future work could potentially extend both the mark-ups and this analysis to 2019. [3]
Our measure is equivalent to TFPRrr in Blackwood et al (2021). [4]
Note that given our MFP measure uses capital stock at the start of the period, Ki,t−1, as an input the timing conventions are the same as used in Decker et al (2020). [5]
We find evidence that capital reallocation is countercyclical, while labour reallocation is procyclical. Still the magnitude of the coefficients is quite small, with around a 2 and 4 percentage point change in unemployment being required, respectively, to equate to the ‘structural’ slowdown that we document in this paper. [6]
Note that for this specification we are effectively lagging MFP given the timing conventions to minimise model changes. [7]
Table B9 also shows the results by ANZSIC division, though the results are not significant for any division, likely reflecting the much smaller samples. [8]
This approach also more directly captures initial size compared to size dummies used elsewhere. [9]
Decker et al (2020) also note that in the presence of non-convex adjustment costs a narrowing in the productivity distribution could lead to a weaker relationship between input growth and productivity. However, Andrews et al (2019) find no evidence of a decline in the dispersion of productivity. [10]
One example would be changes in returns to scale in production. However, our findings of a weakening relationship between input growth and productivity would be consistent with a fall in returns to scale, while most of the literature points to increasing returns to scale. Still, we can't rule out a role for changing returns to scale in production. [11]
Exclusion of intangible capital from the capital stock could also affect our measures of capital, as the measured set of inputs is lower. This would push up measured productivity for firms with large intangible capital stocks. However, as many of these investments are recorded as expenses, intermediate inputs may be overstated. The net effect on measured productivity is ambiguous and will change over time. Similarly, outsourcing is likely to lower measured value added by raising expenses while lowering labour inputs, leading to an ambiguous effect on productivity. [12]
Results are robust to removing the primary sector and are available in the online Supplementary Information. [13]
Available in the online Supplementary Information. [14]
No large firm results available in the online Supplementary Information. [15]
Firms will generally grow along both the capital and labour margin, and so any friction weighing on one could affect the other. However, it may be easier to identify the effects of financing frictions on the factor that they directly impact, given other factors may be subject to some substitution. [16]
Per Decker et al (2020), the role of competition could also be explored based on measures of mark-up dispersion in the context of correlated wedges (i.e. mark-ups rising for more productive firms). But Hambur (forthcoming) finds minimal evidence of increasing dispersion in mark-ups. [17]
Including an interaction between industry and productivity leads to very similar results. [18]
Productivity is taken to be the log level for the purpose of this discussion. [19]
We are implicitly assuming that the production function can be expressed as Yi,t = Ai,t F (Li,t ,Ki,t) where Yi,t is output, Ai,t is MFP and Li,t and Ki,t are labour and capital inputs, respectively. [20]