RDP 2022-09: Estimating the Effects of Monetary Policy in Australia Using Sign-restricted Structural Vector Autoregressions 4. The Effects of a 100 Basis Point Monetary Policy Shock
December 2022
- Download the Paper 1.84MB
The impulse responses presented in Section 3 represent responses to a standard deviation monetary policy shock. However, if we are interested in understanding the effects of, say, increasing the cash rate by 100 basis points, it is necessary to know the effects of a monetary policy shock that raises the cash rate by 100 basis points. Accordingly, I explore the informativeness of the sign restrictions with respect to the impulse responses to a 100 basis point monetary policy shock.
The horizon-h impulse response of variable i to a 100 basis point monetary policy shock is
As discussed in Read (2022b), the identified set for may be unbounded (i.e. infinite in length) when the identified set for the impact response of the cash rate includes zero; intuitively, if , it may be possible to make arbitrarily large by considering a sequence of values for Q converging to the point where Consequently, the set of posterior means and robust credible intervals may also be unbounded. This suggests that sign restrictions may be very uninformative about the impulse responses to a 100 basis point monetary policy shock. Note that I am not claiming that it is reasonable for the cash rate to not respond within the quarter to a monetary policy shock; however, sign restrictions do not necessarily preclude this possibility.
Read (2022b) advocates reporting the posterior probability that , defined as , since this tells us which summaries of the class of posteriors (e.g. robust credible intervals) are guaranteed to be bounded. Table 2 tabulates this probability under the different sets of restrictions. Under Restrictions (1)–(4), ranges between 89 and 100 per cent. This means that the identifying restrictions admit the possibility that the cash rate does not respond on impact to a monetary policy shock with high posterior probability. As a consequence, the set of posterior means, the set of posterior medians and robust credible intervals (at conventional credibility levels) may be unbounded when the parameter of interest is the impulse response to a 100 basis point shock. In fact, is 100 per cent under Restriction (3), so the identified set for may be unbounded at all values of . Restrictions (5) and (6) yield lower values of , but these are still greater than 50 per cent. Together, these results suggest that the sign restrictions may be quite uninformative about the effects of a 100 basis point change in the cash rate.[22]
| Restriction | |||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) |
| 91.8 | 89.1 | 100.0 | 98.8 | 73.1 | 54.9 |
| Note: See Appendix A for details about how these posterior probabilities are approximated. | |||||
Figure 7 plots the posterior median and 68 per cent credible intervals for the impulse responses to a 100 basis point shock obtained under Restriction (6) and a conditionally uniform prior. Based on the posterior median, output is about 2 per cent lower 2 to 3 years after the shock, consumer prices are about 2 per cent lower four years after the shock and the exchange rate appreciates by about 20 per cent on impact. These estimates suggest that monetary policy has potent effects on macroeconomic variables, although the credible intervals convey that there is substantial uncertainty around these estimates. However, even these wide credible intervals substantially overstate the informativeness of the identifying restrictions; for example, a numerical approximation of the set of posterior medians for the output response (not plotted) is extremely wide, with an average width of over 100 percentage points for the horizons considered. This implies that the results obtained under the standard Bayesian approach to inference are largely driven by the conditional prior.
Despite the identifying restrictions appearing to be fairly uninformative about the effects of a 100 basis point shock, we can still draw useful inferences about these effects using the posterior lower and upper probabilities, which are respectively the smallest and largest posterior probabilities that can be assigned to a particular hypothesis given the class of posteriors. Table 3 tabulates the posterior lower probability that the responses of output and prices exceed different thresholds at selected horizons under Restriction (6); that is, the posterior lower probability assigned to the hypothesis given different values of x. The posterior upper probabilities are close to 100 per cent, so I omit them.[23]
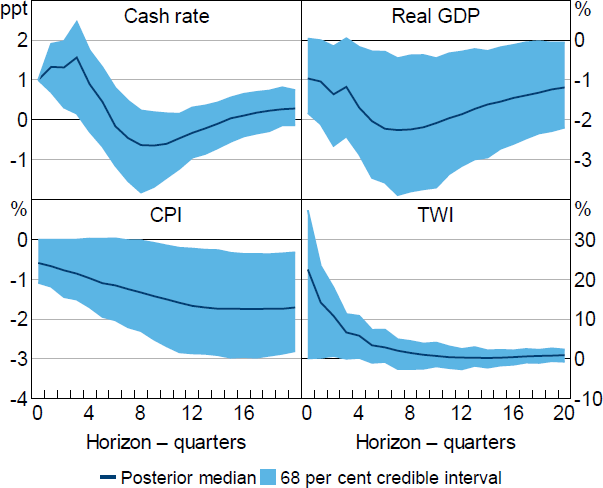
Note: Estimates obtained under Restriction (6), which includes restrictions on impulse responses (cash rate, CPI and TWI), coefficients in the monetary policy reaction function (real GDP, CPI and TWI), and relationship between monetary policy shock and proxy for the shock.
| Horizon | Threshold (%) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Output | Prices | ||||||||||
| 0.0 | –0.25 | –0.5 | –1.0 | –2.0 | 0.0 | –0.25 | –0.5 | –1.0 | –2.0 | ||
| Impact | 75.6 | 38.6 | 14.5 | 3.1 | 1.0 | 100.0 | 22.7 | 11.1 | 2.4 | 0.2 | |
| One year | 86.8 | 81.7 | 61.5 | 22.0 | 3.6 | 80.8 | 30.6 | 15.9 | 5.3 | 0.8 | |
| Two years | 96.3 | 93.7 | 82.1 | 41.0 | 8.7 | 86.0 | 45.8 | 25.3 | 8.7 | 1.3 | |
| Three years | 94.2 | 88.7 | 71.5 | 31.4 | 7.4 | 96.2 | 75.5 | 43.2 | 14.4 | 3.3 | |
| Four years | 91.8 | 82.8 | 57.5 | 23.1 | 5.3 | 99.0 | 87.9 | 57.3 | 19.7 | 4.0 | |
| Note: Posterior lower probability is the smallest posterior probability assigned to the hypothesis (e.g. that output declines by more than 1 per cent at the one-year horizon) within the class of posteriors consistent with Restriction (6). | |||||||||||
Focusing first on the response of output, the posterior lower probability that output declines by more than 0.25 per cent after two years is over 90 per cent and the posterior lower probability that it declines by more than 0.5 per cent is over 80 per cent. There is therefore fairly strong evidence for an appreciable decline in output in response to a 100 basis point shock, in the sense that a decline exceeding 0.5 per cent at the two-year horizon is assigned reasonably high posterior probability under any choice of conditional prior.
Point estimates from previous SVAR analyses of the Australian economy based on zero restrictions suggest that the maximum decline in real GDP following a 100 basis point shock is between 0.2 per cent and 1 per cent (see Figure 3 in Lawson and Rees (2008)). The point estimates from Beckers (2020) also suggest that the peak decline of real GDP is about 1 per cent, although there is substantial uncertainty around this estimate. Based on the RBA's multi-sector dynamic stochastic general equilibrium model, output is estimated to decline by a maximum of about 0.4 per cent (Gibbs et al 2018). The peak response of output in the RBA's macroeconometric model, MARTIN, is also about 0.4 per cent.[24] The results in Table 3 are consistent with the peak response of output lying towards the upper end of this range of estimates, in the sense that – regardless of the choice of conditional prior – fairly large posterior probability is assigned to output responses exceeding the estimates at the lower end of this range. In particular, there is reasonably high posterior lower probability (around 90 per cent) assigned to the hypothesis that the output response after two years exceeds the peak responses in the multi-sector and MARTIN models.
Turning to the response of prices, the posterior lower probability that prices fall by more than 0.25 per cent after three years is around 75 per cent, so there is reasonably robust evidence for an appreciable fall in prices following a 100 basis point shock. The evidence for effects exceeding 1 per cent is less robust; for example, the posterior lower probability that prices decline by more than 1 per cent after three years is only around 15 per cent. For comparison, the point estimates in Beckers (2020) indicate that prices fall by around 0.7 per cent after two or so years, although this estimate is again associated with substantial uncertainty.
Footnotes
The responses to any fixed-size shock (e.g. a 25 basis point shock) can be obtained by linearly rescaling the responses to a 100 basis point shock. The identified set for the response to any given fixed-size shock is consequently unbounded if and only if the identified set for the response to a 100 basis point shock is unbounded. [22]
If is the posterior lower probability assigned to the hypothesis , the posterior upper probability assigned to the hypothesis is . [23]
See Ballantyne et al (2019) for a description of the MARTIN model. The estimates I refer to are from the current version of the model, which differs in some ways from the version described in Ballantyne et al. Note also that the impulse responses to a monetary policy shock presented in Figure 12 of Ballantyne et al correspond to a 100 basis point increase in the cash rate that persists for four quarters, so they are not comparable to the responses discussed in this paper. [24]