RDP 2021-03: Financial Conditions and Downside Risk to Economic Activity in Australia Appendix A: Estimating a Financial Conditions Index for Australia
March 2021
- Download the Paper 1,967KB
A.1 The financial conditions index dataset
The specific series used to estimate the FCI were chosen to cover a broad range of indicators of financial conditions. The rationale is that financial instability can manifest itself, and impact on the real economy, in a wide variety of ways. This means it is not only important to include variables that have historically shown themselves to be relevant (e.g. housing and commercial property prices) but also to include variables that are emerging as potential sources of future risk (e.g. indicators of financial system complexity). The set of variables used in this paper have considerable, though not complete, overlap with those that have been identified as important in other research (e.g. Aikman et al 2018; Prasad et al 2019).
Our main selection criterion was that the series needed to be available at least since the mid 1990s so as to capture as much time variation as possible, particularly given that historical episodes of financial instability in Australia have so far been few and far between.[18] One downside of this approach is that it excludes some measures that are likely to be very relevant today – and going forward – because they do not have sufficiently long histories. Relatedly, the approach is vulnerable to the criticism that it can over-weight measures that happen to be available for longer periods of time.
The resulting set of variables we use can be grouped into the following categories: asset prices (18 series); interest rates and spreads (17); credit and money (14); debt securities outstanding (11); indicators of leverage (5); indicators of banking sector risk (4); indicators of financial system ‘complexity’ (2); indicators of financial market risk (2); and surveys' indicators of businesses' and consumers' views on financial conditions (2). Our dataset spans the sample period 1976:Q3 to 2020:Q3, however, many financial variables we use only have a relatively short history which means our dataset is unbalanced. It starts with 37 series, increases to 54 series by 1987 and to the full dataset of 75 series by mid 1994 but, due to data availability, there are only 42 series for September quarter 2020 (Figure A1).
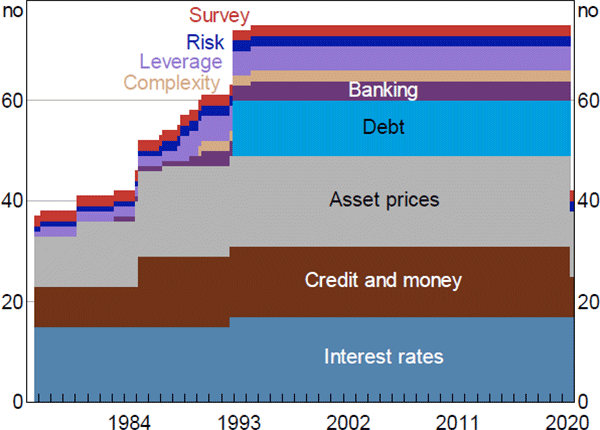
Sources: ABS; ACCI–Westpac; APRA; ASX; Austraclear Limited; Australian Office of Financial Management; Authors' calculations; Bloomberg; CoreLogic; Federal Reserve Bank of St. Louis; MSCI; Private Placement Monitor; RBA; Refinitiv; State borrowing authorities; Westpac and Melbourne Institute
Before estimating the FCI we transform all variables in our dataset to be stationary and standardise them to have zero mean and unit variance.[19] Because all of our variables are nominal, we control for potential structural breaks in the mean of each series in our dataset following the introduction of inflation targeting by the RBA in 1993 by ‘dynamically demeaning’ each series using a rolling 10-year backward-looking estimate of the sample mean (rather than using the full sample mean). Using a rolling estimate of the sample mean allows us to be agnostic about the precise date the break occurred and is preferable to estimating a specific break date for each series in the dataset, which could be subject to large estimation uncertainty.[20] The choice of a 10-year window follows Kamber, Morley and Wong (2018), but is not specifically related to the length of business or financial cycles in our case. Note, dynamically demeaning all series even if no series has a structural break in the mean should not cause any estimation problems. If there is no structural break in a particular series then the rolling window estimated sample mean for that series should be equal to its full sample mean.
Some previous papers have ‘purged’ the financial data of correlations with measures of economic activity before estimating the FCI by using the residuals from regressions of the financial variables on a set of variables related to ‘macroeconomic conditions’ (e.g. Hatzius et al 2010). However, we follow Kapetanios et al (2017) who argue that purging the data with a prior regression may reduce its usefulness as a summary measure. For example, if the only common shock in the economy at a given point in time was financial in nature, then this type of analysis would amount to purging the financial series of precisely the information we are aiming to summarise. Table A1 provides a complete list of all series we use to estimate the FCI and specifies the source, the start and end dates as well as the specific transformation we apply to each series.
| No | Variable | Source | Economy | Start date | End date | Transformation code |
|---|---|---|---|---|---|---|
| Survey measures | ||||||
| 1 | Business: difficulty getting finance | ACCI-WBC | Aus | 1966:Q2 | 2020:Q3 | FD |
| 2 | Consumer: family finances now | WBC-MI | Aus | 1974:Q4 | 2020:Q3 | LV |
| Interest rates and spreads | ||||||
| 3 | Overnight cash rate (OCR) | RBA | Aus | 1976:Q3 | 2020:Q3 | FD |
| 4 | 3-month bank bill rate | ASX; RBA | Aus | 1976:Q3 | 2020:Q3 | FD |
| 5 | 3-year Australian Government security (AGS) yield | RBA | Aus | 1992:Q3 | 2020:Q3 | FD |
| 6 | 5-year AGS yield | RBA | Aus | 1976:Q3 | 2020:Q3 | FD |
| 7 | 10-year AGS yield | RBA | Aus | 1969:Q3 | 2020:Q3 | FD |
| 8 | Spread: 3-month bank bill to OCR | ASX; RBA | Aus | 1972:Q1 | 2020:Q3 | LV |
| 9 | Spread: 3-year AGS to OCR | RBA | Aus | 1992:Q3 | 2020:Q3 | LV |
| 10 | Spread: 5-year AGS to OCR | RBA | Aus | 1969:Q3 | 2020:Q3 | LV |
| 11 | Spread: 10-year AGS to OCR | RBA | Aus | 1976:Q3 | 2020:Q3 | LV |
| 12 | Federal funds rate (FFR) | FRED | US | 1959:Q3 | 2020:Q3 | FD |
| 13 | 3-month Treasury bill (Tbill) yield | FRED | US | 1959:Q3 | 2020:Q3 | FD |
| 14 | 3-year Treasury bond (TB) yield | FRED | US | 1959:Q3 | 2020:Q3 | FD |
| 15 | 10-year TB yield | FRED | US | 1959:Q3 | 2020:Q3 | FD |
| 16 | Spread: 3-month Tbill to FFR | FRED | US | 1959:Q3 | 2020:Q3 | LV |
| 17 | Spread: 3-year TB to FFR | FRED | US | 1959:Q3 | 2020:Q3 | LV |
| 18 | Spread: 10-year TB to FFR | FRED | US | 1959:Q3 | 2020:Q3 | LV |
| 19 | Spread: 10-year AGS to 10-year USTB | RBA; FRED | Aus/US | 1969:Q3 | 2020:Q3 | LV |
| Credit and money | ||||||
| 20 | Total credit | RBA | Aus | 1976:Q3 | 2020:Q3 | LD |
| 21 | Housing credit | RBA | Aus | 1976:Q3 | 2020:Q3 | LD |
| 22 | Personal credit | RBA | Aus | 1976:Q3 | 2020:Q3 | LD |
| 23 | Business credit | RBA | Aus | 1976:Q3 | 2020:Q3 | LD |
| 24 | Owner-occupier housing loan approvals (excl refinancing) | ABS | Aus | 1985:Q1 | 2020:Q2 | LD |
| 25 | Investor housing loan approvals (excl refinancing) | ABS | Aus | 1985:Q1 | 2020:Q2 | LD |
| 26 | Commercial fixed term loan approvals (excl refinancing) | ABS | Aus | 1985:Q1 | 2020:Q2 | LD |
| 27 | Commercial revolving credit approvals (excl refinancing) | ABS | Aus | 1985:Q1 | 2020:Q2 | LD |
| 28 | Personal fixed term loan approvals (excl refinancing) | ABS | Aus | 1985:Q1 | 2020:Q2 | LD |
| 29 | Personal revolving credit approvals (excl refinancing) | ABS | Aus | 1985:Q1 | 2020:Q2 | LD |
| 30 | M1 | RBA | Aus | 1975:Q1 | 2020:Q3 | LD |
| 31 | M3 | RBA | Aus | 1976:Q3 | 2020:Q3 | LD |
| 32 | Broad money | RBA | Aus | 1976:Q3 | 2020:Q3 | LD |
| 33 | Money base | RBA | Aus | 1975:Q1 | 2020:Q3 | LD |
| Asset prices | ||||||
| 34 | Dwelling price index | CoreLogic | Aus | 1980:Q1 | 2020:Q3 | LD |
| 35 | House price index | CoreLogic | Aus | 1980:Q1 | 2020:Q3 | LD |
| 36 | Apartment price index | CoreLogic | Aus | 1980:Q1 | 2020:Q3 | LD |
| 37 | Dwelling price index | FRED | US | 1987:Q1 | 2020:Q2 | LD |
| 38 | All commercial property return index | MSCI | Aus | 1984:Q4 | 2020:Q2 | LD |
| 39 | Retail property return index | MSCI | Aus | 1984:Q4 | 2020:Q2 | LD |
| 40 | Office property return index | MSCI | Aus | 1984:Q4 | 2020:Q2 | LD |
| 41 | Industrial property return index | MSCI | Aus | 1984:Q4 | 2020:Q2 | LD |
| 42 | ASX 200 Index | Refinitiv | Aus | 1973:Q1 | 2020:Q3 | LD |
| 43 | ASX 200 Financials Index | Refinitiv | Aus | 1973:Q1 | 2020:Q3 | LD |
| 44 | ASX 200 Real Estate Index | Refinitiv | Aus | 1973:Q1 | 2020:Q3 | LD |
| 45 | ASX 200 Resources Index | Refinitiv | Aus | 1973:Q1 | 2020:Q3 | LD |
| 46 | ASX 200 Industrials Index | Refinitiv | Aus | 1973:Q1 | 2020:Q3 | LD |
| 47 | S&P 500 Index | FRED | US | 1960:Q1 | 2020:Q3 | LD |
| 48 | RBA Index of Commodity Prices (AUD) | RBA | Aus | 1959:Q3 | 2020:Q3 | LD |
| 49 | Gold (3pm London bullion market, USD) | FRED | US | 1968:Q2 | 2020:Q3 | LD |
| 50 | Crude oil (West Texas intermediate, USD) | FRED | US | 1968:Q2 | 2020:Q3 | LD |
| 51 | Australian dollar trade-weighted index | RBA | Aus | 1970:Q3 | 2020:Q3 | LD |
| Debt securities outstanding | ||||||
| 52 | Short-term: Australia: banks | APRA; Austraclear Limited; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 53 | Short-term: Australia: non-financial corporations | Austraclear Limited; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 54 | Long-term: banks | Bloomberg; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 55 | Long-term: Australia: non-financial corporations | Bloomberg; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 56 | Short-term: Australia: government | AOFM; Austraclear Limited; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 57 | Long-term: Australia: government | AOFM; RBA; State borrowing authorities | Aus | 1992:Q4 | 2020:Q2 | LD |
| 58 | Long-term: overseas: non-government | ABS; Bloomberg; Private Placement Monitor; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 59 | Short-term: Australia: asset-backed securities | ABS; Bloomberg; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 60 | Long-term: Australia: asset-backed securities | ABS; Bloomberg; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 61 | Long-term: overseas: asset-backed securities | ABS; Bloomberg; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| 62 | Residential mortgage-backed securities | ABS; Bloomberg; RBA | Aus | 1992:Q4 | 2020:Q2 | LD |
| Banking sector | ||||||
| 63 | Tier 1 capital ratio | APRA; RBA | Aus | 1989:Q2 | 2020:Q2 | FD |
| 64 | Non-performing assets ratio | APRA; RBA | Aus | 1990:Q2 | 2020:Q2 | FD |
| 65 | Distance to default | RBA | Aus | 1983:Q1 | 2020:Q2 | LV |
| 66 | Wholesale debt spread to AGS | Bloomberg; RBA | Aus | 1994:Q2 | 2020:Q2 | FD |
| Financial system complexity (ratio) | ||||||
| 67 | Total financial institutions' assets to nominal GDP | ABS; RBA | Aus | 1990:Q1 | 2020:Q2 | LD |
| 68 | Total off-balance sheet business to total fixed income assets | ABS; RBA | Aus | 1990:Q1 | 2020:Q2 | LD |
| Leverage measures (ratio) | ||||||
| 69 | Household debt to assets | ABS; RBA | Aus | 1988:Q3 | 2020:Q2 | LD |
| 70 | Household debt to income | ABS; RBA | Aus | 1988:Q2 | 2020:Q2 | LD |
| 71 | Household interest payments to income | RBA | Aus | 1977:Q1 | 2020:Q2 | LD |
| 72 | Current account balance to nominal GDP | ABS | Aus | 1959:Q3 | 2020:Q2 | FD |
| 73 | Net total foreign liabilities to nominal GDP | ABS | Aus | 1988:Q3 | 2020:Q2 | FD |
| Risk indicators | ||||||
| 74 | Chicago Board Options Exchange equity volatility | FRED | US | 1986:Q4 | 2020:Q3 | LV |
| 75 | Moody's corporate bond yield spread: BAA to AAA | FRED | US | 1959:Q3 | 2020:Q3 | LV |
| Notes: ‘ABS’ is Australian Bureau of Statistics, ‘ACCI-WBC’ is Australian Chamber of Commerce and Industry–Westpac, ‘AOFM’ is the Australian Office of Financial Management, ‘FRED’ is Federal Reserve Economic Database, Federal Reserve Bank of St. Louis, ‘WBC-MI’ is Westpac and Melbourne Institute; ‘Transformation code’ indicates the method used to transform the data to be stationary if necessary, ‘FD’ indicates first difference, ‘LD’ indicates log difference and ‘LV’ indicates level | ||||||
A.2 Constructing the financial conditions index
The general form of the DFM we use to estimate the FCI follows Bai and Wang (2015) and is defined as:
where yt is N × 1 vector of observables, ft is a q × 1 vector of the dynamic factors, and is the dynamic factor loadings for ft – j with j = 0,1,...,s and t = 1,...,T. The dynamic factors follow a VAR(p) process with a q × q matrix of autoregressive coefficients (with all roots outside the unit circle). The number of dynamic factors is q (the dimension of ft) which is irrespective of s and p.
The covariance matrix of in the measurement equation is given by R with dimension N × N and is restricted to be a diagonal matrix. In the state equation, the covariance matrix of corresponds to the q × q matrix Q. We assume that (i.e. the 2 noise processes are independent). This specification of the DFM has 2 different sources of dynamics. First, there are s lagged factors representing a dynamic relationship between the observable series yt and the factors ft. Second, the dynamics of the factors is assumed to be captured by a VAR(p) process. Bai and Wang (2015) argue that it is the first source of dynamics that makes this specification a true dynamic factor model because it is these dynamics that make the biggest distinction between dynamic and static factor analysis.[21] The state-space representation of the DFM specified by Equation (A2) is:
The measurement equation takes the form of a static factor model (Stock and Watson 2002) with r = q (s + 1) static factors. Now, define k = max(p,s + 1) and set if k = s + 1 > p.
Let , then the N × qk factor loadings matrix the qk × qk matrix of VAR coefficients and the qk × q selector matrix G have the following form:
when k = p > s, let be a subvector of Ft. Then the factor loadings matrix and the VAR coefficient matrix become:
Note, the selector matrix G does not change in this alternative setting. The benefit of this modelling strategy over others, such as traditional static factor models based on principal components analysis (PCA), is that it explicitly incorporates dynamics into the estimation and can easily and efficiently handle unbalanced datasets such as the one we use.
When implementing the DFM we assume one common factor (i.e. q = 1) is adequate to capture the common variation we are most interested in from our dataset. This decision was made because we want a single index to represent ‘financial conditions’. Multiple factors would require us to combine them into a single index and it is unclear what the optimal way to do this is. Moreover, the modified Bai and Ng (2002) information criterion proposed by Coroneo, Giannone and Modugno (2016) suggests one factor is sufficient.[22]
The dynamics of the factor are assumed to follow an AR(1) process (i.e. p = 1). This was determined by the Schwarz information criterion (SIC), together with plots of the sample autocorrelation function (ACF) and sample partial ACF for the common factor based on an initial estimate of the common factor obtained by PCA.
We choose to include one lag of the factor in the measurement equation (i.e. s = 1) because some of the series in our dataset are market determined. These series will tend to be less persistent (and potentially more volatile) than the other series in our dataset which are not market determined. A DFM with dynamic loadings will be able to accommodate this explicitly.
Following Doz, Giannone and Reichlin (2011, 2012) we estimate the DFM by quasi-maximum likelihood.[23] Estimation consists of 2 parts. First, the parameters of the state-space representation of the DFM are obtained by applying PCA to a balanced subset of the dataset which contains all 75 series. Second, the Kalman filter is applied on the original unbalanced dataset in order to obtain estimates of the factors using only the information available at each point in time.
For the observations Y = {y1,...,yT}, factors F = {F1,...,FT} and parameter vector the complete data log likelihood is given by:
We estimate the parameter vector using the expectation-maximisation (EM) algorithm and the Kalman filter and Rauch-Tung-Striebel (RTS) smoother recursions (for more details, see Anderson and Moore (1979)). To do this, we set the initial values in the state-space equations using the first r principal components-based estimates of the factors and OLS estimates of the parameters and Q treating the principal components factors as the true common factors. From these starting values we then alternate between 2 steps. First, we estimate the expected value of the common factors given the data and previously estimated model parameters (the ‘E-step’). This involves running the Kalman filter and RTS smoother recursions and getting a new estimate of the common factors denoted by where is the vector of estimated model parameters from the previous step. Then using these updated estimates of the common factors we compute new parameter estimates by maximising the expected log likelihood with respect to (the ‘M-step’).
To account for missing observations in yt we define the known matrix Wt which is a diagonal matrix of size N with the ith diagonal element equal to zero if yi,t is missing and equal to one otherwise. The matrix Wt acts a selector matrix and ensures only the available data are used in the Kalman filter and RTS smoother recursions. The updating equations for the parameters and Q are as follows:
To compute the next we use:
To compute the next we use:
To compute the next R we use:
To compute the next Q we use:
The initial state F0 and initial state variance P0 are given by:
See Ghahramani and Hinton (1996) and Bańbura and Modugno (2014) for more details on these calculations. We judge convergence to be when cm is less than 10–4, with cm given by:
and m = 1,...,M is the number of evaluations needed to achieve convergence up to a maximum M set by the researcher. We set M = 500 but we only needed 8 evaluations in our case.
A convenient feature of this specification is that the computational complexity of the Kalman filter and RTS smoother recursions depends only on the size of the state. In our case this corresponds to r and is independent of the size of the cross-section N. Note, while the EM algorithm will converge to a maximum, it is not guaranteed to find the global maximum and can converge to a local maximum. We can reduce the probability of this occurring by starting the algorithm with the PC-based estimates which are consistent for large cross-sections (see Stock and Watson (2002) and Bai and Ng (2002)).
A common issue with estimating factor models is the lack of identification. In our case this means the likelihood of our model is invariant to any invertible linear transformation of the factors. That is, for any invertible matrix H the parameters = and are observationally equivalent and hence is not identifiable from the data. In order to achieve identifiability of , we need to impose an identifying restriction. We implement the restriction ‘DFM2’ suggested by Bai and Wang (2015).[24] This identifying restriction specifies the first q × q block of in to be an identity matrix:
where is an (N – q) × q unrestricted block of . This parameterisation of is also called the ‘named factor’ normalisation because it associates each factor with a specific variable (Stock and Watson 2016).
When implementing this identifying restriction it is important to order the variables in Y so that the first q variables are the naming variables. In practice, the naming variables need to be reasonably different from each other and sufficiently representative of groups of other variables so that the innovations to their common components span the same space as the factor innovations. In our work we choose to put the series ‘survey: difficulty getting finance for business’ as the first series. Increases in this series reflect greater difficulty for businesses getting access to finance while decreases in this series reflect less difficulty for businesses in getting access to finance. A benefit of this normalisation is that it also identifies the sign of the estimated common factor. It is common for more restrictive financial conditions to be reflected by increases in the FCI and for more expansionary financial conditions to be reflected by decreases in the FCI (see Brave and Butters (2010)). Hence, being able to impose this sign convention with our FCI is beneficial. The named factor normalisation means the interpretation of the factor loadings on the other variables changes. They become measures of the correlation of each series with the factor relative to the named factor series.
To impose this identifying linear restriction in estimation we need to modify the M-step used to estimate to incorporate the linear restriction specified by:
where is a selector matrix with dimension q2 × (N × r) with 0 or 1 elements specifying the coefficients that will be restricted. The vector is of dimension q2 × 1 also with 0 or 1 elements and are the values that the coefficients will be restricted to be. The updating equation incorporating the identifying restriction for becomes:
where is the estimated factor loadings with the identifying restriction and is the unrestricted estimated factor loadings given previously by Equation (A6), see Wu, Pai and Hosking (1996) and Bańbura and Modugno (2014) for more information.
A.3 Which series are most important for financial conditions?
The sign and magnitude of the combined values of the 2 factor loadings for each series indicate the relative strength and direction of that series' relationship with the estimated FCI. Figure A2 highlights the 10 most important series by positive and negative combined weights. Series with a negative (positive) combined weight tend to move in the opposite (same) direction to the FCI, falling (rising) when the FCI indicates financial conditions are restrictive and rising (falling) when the FCI indicates financial conditions are expansionary.
The series which are most strongly related to the contemporaneous value of the FCI tend to have negative weights. These same series also tend to be negatively related to the one-period lag of the FCI as well. These include property prices, growth in credit aggregates and one survey measure related to consumer expectations of their finances. Of these, commercial property has the highest combined weighting and as a result has the strongest relationship with the FCI. This is unsurprising given the highly procyclical nature of commercial property returns during the only 2 episodes of significant financial instability in our sample. Coupled with the fact that the commercial property sector has historically been a relatively important source of risk to banks' balance sheets (Ellis and Naughtin 2010), these results underscore the importance of monitoring developments in this sector on an ongoing basis.
In contrast, only one-quarter of the dataset are positively related to the FCI, with the magnitude of the combined weights typically much smaller than those series with negative signs. The strongest positive correlations belong mostly to interest rate spreads. Note, we have not included the series ‘survey: difficulty getting finance for business’ since the first factor loading is restricted to be unity by design (see Appendix A.2).
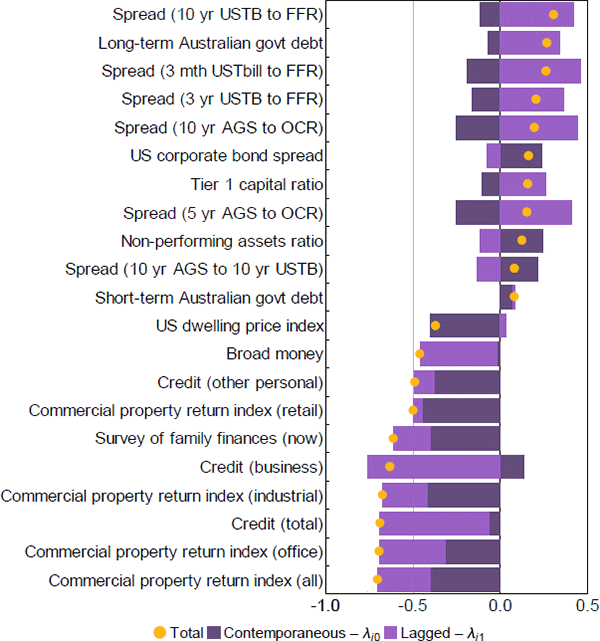
Note: Weights are the estimated factor loadings for each series excluding the named factor series ‘survey: difficulty getting finance for business’
Sources: ACCI–Westpac; APRA; Austraclear Limited; Australian Office of Financial Management; Authors' calculations; CoreLogic; Federal Reserve Bank of St. Louis; MSCI; RBA; State borrowing authorities; Westpac and Melbourne Institute
A.4 Robustness checks for the FCI
We undertake 2 checks of our preferred estimated FCI to confirm its soundness as a measure of financial conditions. The first is a comparison of the DFM methodology against an alternative method for estimating the FCI. The second is a comparison of our preferred estimated FCI (estimated using the DFM approach) and the named factor series ‘survey: difficulty getting finance for business’. The named factor series is the one we choose to restrict the factor loading to be unity in estimation for identification purposes. Both comparisons are shown in Figure A3.
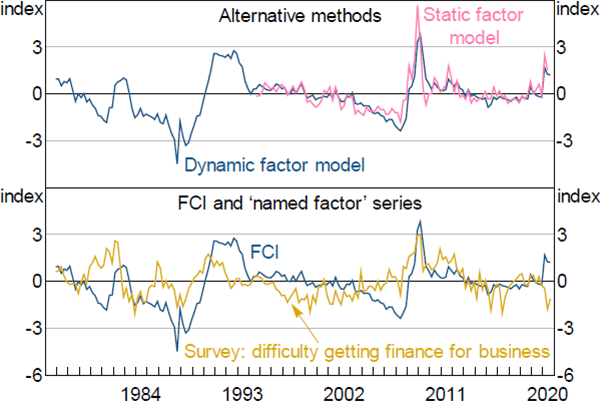
Notes: The ‘Static factor model’ estimates were renormalised to match the profile of the dynamic factor model FCI; the ‘named factor’ series has been standardised to have zero mean and unit variance
The top panel compares our preferred estimated FCI with another FCI produced using a static factor model (SFM). The DFM technique is preferable to the SFM technique since it allows the FCI to be estimated over a longer time period (SFMs are estimated by PCA and require balanced datasets). Further, since the DFM explicitly incorporates dynamics, it produces an indicator that appears smoother than the indicator based on the SFM estimate.
The bottom panel shows the estimated FCI and the named factor series ‘survey: difficulty getting finance for business’. Both series display a reasonably similar ‘low frequency’ pattern, but the movements between the two series are not exactly the same. This shows that the named factor series is not significantly influencing the profile of the estimated FCI besides helping to identify its scale, as intended.
A further robustness check of the DFM methodology is to formally test whether the dataset as a whole supports the inclusion of a lag of the factor in the measurement equation. We test this using a likelihood ratio ( LR ) test.[25] This is easy to do since we get the log likelihood as a by-product of the Kalman filter. To compute the LR statistic we estimate the DFM twice. Once with the lag included to get the value of the unrestricted log likelihood and again with the lag excluded to get the value of the restricted log likelihood The LR test statistic is then computed as:
where k is the number of restrictions to be tested. Under the null hypothesis the test is distributed as chi-squared with k degrees of freedom. The test result is shown in Table A2. The test statistic is very large at 1,091 and with k = 75 parameter restrictions the associated p-value is effectively zero.
This suggests there is little evidence against the DFM methodology we have used to construct the FCI.
| Number of parameter restrictions ( k ) | 75 |
|---|---|
| Unrestricted log likelihood ( ) | −16,145.5 |
| Restricted log likelihood ( ) | −16,691.2 |
| Test statistic | 1,091.4 |
| p-value | 0.0 |
| Note: Test statistic is computed as −2 which is distributed as chi-squared with k degrees of freedom under the null | |
A.5 Assessing the relationship between financial conditions and economic outcomes
We start by assessing the FCI's ability to predict 5 separate summary measures of economic activity: real GDP, real household final consumption expenditure, the unemployment rate, employment and real non-mining business investment. We examine both quarterly and year-ended changes in these variables over the period 1976:Q4 to 2020:Q2.[26]
Figure A4 plots the FCI against the 5 measures of economic activity for quarterly and year-ended time horizons. Each series has been standardised to have zero mean and unit variance. Most series exhibit reasonable contemporaneous relationships with the FCI, although the strength varies. Four of the measures of economic activity are negatively related to financial conditions (more restrictive financial conditions correspond to weaker growth), while change in unemployment rate has a positive relationship (more restrictive financial conditions are associated with an increase in the unemployment rate).
Estimates of the sample cross-correlation between the measures of activity and the FCI for both time horizons are provided in Table A3.
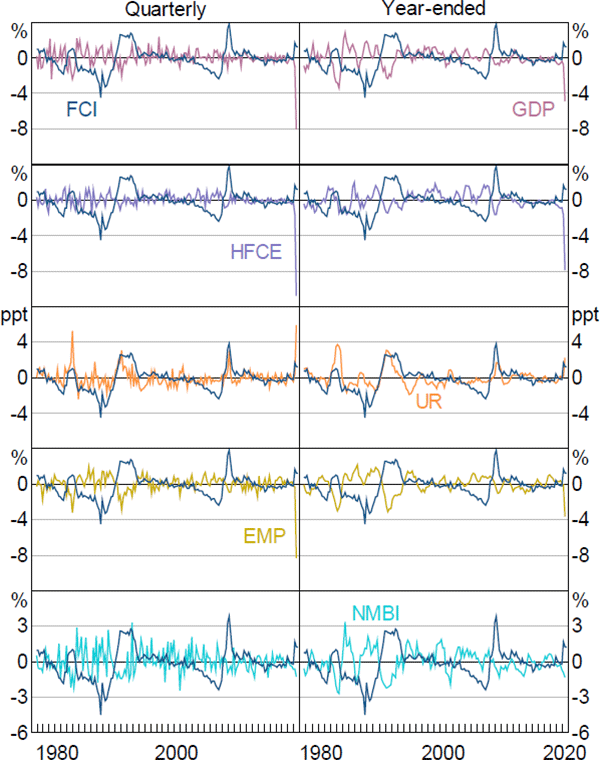
Notes: All economic activity series are standardised to have zero mean and unit variance; ‘GDP’ is the growth rate of real gross domestic product; ‘HFCE’ is the growth rate of real household final consumption expenditure; ‘UR’ is the change in the total unemployment rate; ‘EMP’ is the growth rate of total employment; ‘NMBI’ is the growth rate of real business investment excluding mining investment
Sources: ABS; Authors' calculations; RBA
The contemporaneous sample correlations between the measures of economic activity and the FCI are strongest for the 2 labour market variables and weakest for consumption. Across variables, correlations tend to be stronger for year-ended, rather than quarterly, changes reflecting the fact that year-ended changes are relatively smoother. The sample cross-correlation between these measures of economic activity and the FCI at different lag lengths suggest there might be a lead/lag relationship between the FCI and the various measures of economic activity.
| Quarterly | Year-ended | ||||||
|---|---|---|---|---|---|---|---|
| Contemporaneous | Maximum(a) | Lag(b) | Contemporaneous | Maximum(a) | Lag(b) | ||
| GDP | −0.27 | −0.27 | 0 | −0.43 | −0.45 | 1 | |
| Consumption | −0.21 | −0.22 | 1 | −0.30 | −0.35 | 1 | |
| Unemployment rate | 0.44 | 0.44 | 0 | 0.51 | 0.55 | 1 | |
| Employment | −0.46 | −0.47 | 1 | −0.60 | −0.67 | 1 | |
| Business investment | −0.28 | −0.28 | −1 | −0.46 | −0.46 | 0 | |
|
Notes: All series are in growth rates besides the unemployment rate which is in differences
|
|||||||
However, sample cross-correlations between two serially correlated time series can sometimes indicate spurious relationships (see Cryer and Chan (2008)). To formally assess these potential lead/lag relationships we use Granger causality tests. This attempts to determine if the lags of one time series have information that is useful for predicting another time series over and above the information already contained in the lags of that second series. The test can be sensitive to the choice of lag length, so we test for lag lengths from one to four quarters.[27] We can infer Granger causality when there is evidence that the FCI Granger-causes the measure of economic activity and no evidence that the measure of economic activity Granger-causes the FCI. The results are in Table A4.
The results suggest that the FCI does contain predictive information about the 5 measures of economic activity at a quarterly time horizon, although the results for household consumption are only significant at the 10 per cent level for the first lag. At a year-ended time horizon the results are similar for GDP, household consumption, the unemployment rate and employment. In contrast, the FCI only provides additional predictive information for business investment at longer lag lengths (i.e. lags greater than 2).
| Lag length | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Quarterly | ||||
| GDP does not Granger-cause FCI | 0.85 | 1.00 | 1.00 | 1.00 |
| FCI does not Granger-cause GDP | 0.02 | 0.00 | 0.00 | 0.00 |
| HFCE does not Granger-cause FCI | 1.00 | 1.00 | 1.00 | 1.00 |
| FCI does not Granger-cause HFCE | 0.09 | 0.00 | 0.01 | 0.01 |
| UR does not Granger-cause FCI | 1.00 | 1.00 | 1.00 | 1.00 |
| FCI does not Granger-cause UR | 0.00 | 0.00 | 0.00 | 0.00 |
| EMP does not Granger-cause FCI | 0.74 | 0.23 | 0.26 | 0.74 |
| FCI does not Granger-cause EMP | 0.00 | 0.00 | 0.00 | 0.00 |
| NMBI does not Granger-cause FCI | 0.78 | 0.92 | 0.72 | 0.85 |
| FCI does not Granger-cause NMBI | 0.00 | 0.02 | 0.00 | 0.00 |
| Year-ended | ||||
| GDP does not Granger-cause FCI | 1.00 | 1.00 | 1.00 | 1.00 |
| FCI does not Granger-cause GDP | 0.02 | 0.00 | 0.00 | 0.00 |
| HFCE does not Granger-cause FCI | 0.43 | 0.73 | 0.28 | 0.59 |
| FCI does not Granger-cause HFCE | 0.06 | 0.00 | 0.00 | 0.03 |
| UR does not Granger-cause FCI | 0.27 | 1.00 | 1.00 | 1.00 |
| FCI does not Granger-cause UR | 0.00 | 0.00 | 0.00 | 0.00 |
| EMP does not Granger-cause FCI | 0.61 | 0.90 | 1.00 | 1.00 |
| FCI does not Granger-cause EMP | 0.00 | 0.00 | 0.00 | 0.00 |
| NMBI does not Granger-cause FCI | 1.00 | 1.00 | 1.00 | 1.00 |
| FCI does not Granger-cause NMBI | 0.04 | 0.11 | 0.00 | 0.00 |
| Notes: All p-values have been adjusted using the Bonferroni correction method; ‘GDP’ is the growth rate of real gross domestic product; ‘HFCE’ is the growth rate of real household final consumption expenditure; ‘UR’ is the change in the total unemployment rate; ‘EMP’ is the growth rate of total employment; ‘NMBI’ is the growth rate of real business investment excluding mining investment | ||||
Footnotes
This decision also has a practical purpose. We initialise our DFM using parameter estimates derived from principal components analysis which requires a balanced dataset. Hence, a dataset with lots of very short series could result in less precise starting values which will affect the estimation of the FCI. [18]
Variables are made stationary by taking logs and/or differences as appropriate. [19]
This will also be useful to correct for any structural drift in the mean of any series as well. [20]
Bai and Wang regard the specification to be a static factor model when there are no lags in the measurement equation (i.e. s = 0). [21]
Note, this information criterion is only designed to be used to determine the number of static factors in a dataset and not the number of dynamic factors in a dataset. Our dynamic factor model with one factor and one lag can be rewritten as a static factor model with 2 factors. As a robustness check we test whether the inclusion of the lag (i.e. the second static factor) is supported by the data and we find that it is. These results are in Appendix A.4. [22]
Estimation is ‘quasi’ maximum likelihood because the model is misspecified. This comes from assuming that R the covariance matrix of the idiosyncratic component is diagonal. Additionally, we also assume that both noise processes are Gaussian. However, in large samples, this has been shown to be no issue (see Doz et al (2012), Bai and Li (2016) and Barigozzi and Luciani (2019)). [23]
The identifying restriction ‘DFM2’ is similar to the identifying restrictions ‘PC3’ suggested by Bai and Ng (2013) and ‘IC1’ suggested by Bai and Li (2016). [24]
Our decision to use the LR test relies on Bai and Wang (2015)'s suggestion that a Wald test for parameter restrictions in the DFM is feasible and a Wald test is asymptotically equivalent to a LR test (see Buse (1982)). [25]
The original frequency of the unemployment rate and the employment series is monthly. We convert both series to a quarterly frequency by taking the quarter-ended monthly value. [26]
We chose to use a maximum of 4 lags based on sample cross-correlation analysis in Table A2. [27]