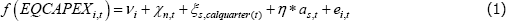RDP 2018-07: The GFC Investment Tax Break 6. DD with Capex Survey Data
June 2018
- Download the Paper 1.8MB
As discussed above, the DD approach examines differences in the behaviour of the treatment and control groups, in the treatment and non-treatment periods. In our analysis, we take businesses with revenue below $2 million in the previous financial year to be our treatment group, and other businesses to be our control group.
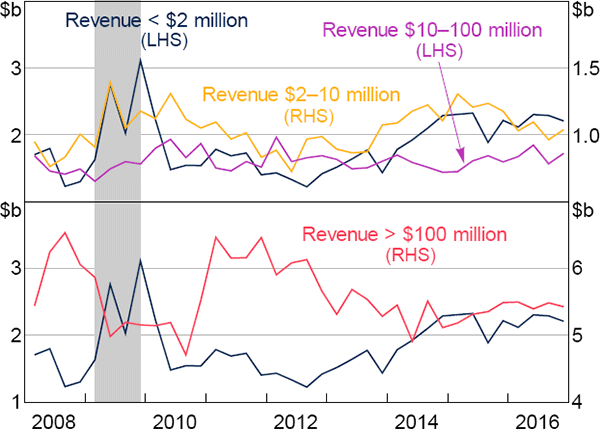
Again, we start by providing a graphical analysis. Figure 7 presents total equipment capex in Australia, disaggregated by revenue of the responsible business for the previous year. These data show a very clear distinction between the businesses eligible for the highest tax break rate and larger businesses during the period that the differential tax break was in effect. Equipment capex by businesses with revenue below $2 million was 58 per cent higher in 2009 than in 2008, and 40 per cent higher in 2009 than in 2010. In contrast, equipment capex by businesses with revenue between $2 million and $10 million, who were not eligible for the 50 per cent bonus rate, was only 28 per cent higher in 2009 than in 2008, and was about the same in 2009 as in 2010. Further graphical analysis of the tax break using aggregate data is provided in Rodgers (2017).
Note: Employing businesses in non-mining divisions
Source: ABS
These data also indicate reasonably parallel trends between the treatment and control groups in the non-treatment periods (2008 and 2010 onwards). Small business investment began to rise from 2013 onwards, which coincides with a number of other tax changes introduced for these businesses.
6.1 Econometric Methodology
We estimate a DD model using business-level data. We model the extensive margin (i.e. whether they invest) and the intensive margin (i.e. how much they invest, conditional on investing) separately, as in ZM. Most small businesses do not invest in a given quarter, so this approach allows us to use all of the data.
The generic specification for the models is given below. For the intensive margin model, the dependent variable (f(EQCAPEXi,t)) is the natural log of equipment capex (zero observations are excluded). For the extensive margin model, the dependent variable is the log-odds of EQCAPEXi,t > 0, calculated at the division-turnover category level, as in ZM.[20] Aggregating the extensive margin dependant variable in this way allows us to include fixed effects without losing data on businesses that invest in every quarter (or no quarters).
In the specification, i denotes a business, s denotes the revenue size categories (< $2 million, $2–10 million, $10–100 million, and > $100 million), n denotes ANZSIC divisions, and t denotes time (which is quarterly in this dataset). The explanatory variables are:
- Business fixed effects (νi): these control for characteristics of each business that drive investment but do not vary over time.
- Industry-quarter dummy variables (Χn,t): These control for differing conditions across industries during our sample period. In particular, they control for different industry experiences during the GFC.
- Seasonal dummy variables by size bucket (ξs,calquarter(t)): These control for differing seasonal patterns across businesses of different size.
- The level of the investment tax break (as,t): This is our treatment variable, and we parameterise it with the data shown in Figure 1.[21] Treatment intensity differs between small and large businesses in the final three quarters of the 2009 calendar year. These differences allow us to estimate η, the semi-elasticity of investment with respect to the tax break.
We estimate this model using data from the first quarter of 2008, as we cannot measure the business size for earlier capex observations. We stop the estimation in the middle of 2012 to abstract from the effect of other investment tax breaks for small businesses.[22]
Businesses in the revenue categories above $2 million – who received lower levels of the investment tax break – are the control group in this DD set-up. Our basic identification assumption is that differences in equipment capex between businesses with revenue below $2 million and this control group are entirely due to the investment tax break. To be more nuanced, this comparison is done after accounting for the average difference in equipment capex between small and large businesses within each industry across time. Or to put it another way, we are comparing investment for small and large businesses within each industry.
We use the $2 million to $10 million revenue size category as our baseline control group, but we also present results using a broader control group. Our motivation for concentrating on the narrower control group is that the parallel trends assumption required for identification seems more reasonable for small and medium businesses, than for small and large businesses. It seems more likely that conditions during the crisis would have affected investment by small and medium businesses similarly, compared with small and large businesses. A further issue is that ZM found that larger businesses have a weaker response to tax breaks. Heterogeneity of this type will bias our estimate of η upwards.
6.2 Baseline Results
Table 6 contains the baseline results from the intensive margin DD model for the Capex Survey dataset. When the control group is businesses with revenue in the $2–10 million range, the estimated semi-elasticity is around 1, and is statistically significant at the 1 per cent level. This translates into a 10 per cent increase in equipment capex in response to a 10 percentage point increase in the investment tax break, and an elasticity of investment with respect to the cost of capital of 2.5. When the control group is all businesses with revenue above $2 million, the estimated semi-elasticity is bit larger.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 0.98*** (0.30) |
1.40*** (0.18) |
| Clusters (businesses) | 5,724 | 11,019 |
| Business fixed effects | Yes | Yes |
| Observations | 14,379 | 58,856 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the business level |
||
This baseline semi-elasticity from the DD model is slightly below the range estimated using the RD model. We think the most likely reason for this is that the estimate from the RD model is very local and is potentially only valid for the small range of businesses used in the estimation. The estimate from the DD model applies to a broader range of businesses, though the causal identification is less robust. In this sense, they are both ‘true’ estimates of the effect, but for different samples of businesses.
There are also some factors that could potentially be biasing our estimates from the DD model towards zero:
- The rule used to determine whether businesses are small when using the Capex Survey data could misclassify some small businesses as large. Some businesses might have been able to qualify as small based on having revenue below $2 million two years ago. If there are a large number of such businesses, under our maintained hypothesis this would bias our results down. The spike in investment by businesses in the $2–10 million bracket in June quarter 2009 would be consistent with this story. Businesses with revenue below $2 million in 2006/07, above in 2007/08, and that also met the expectational requirement, would have a strong incentive to take advantage of larger deductions before they start being considered large businesses for tax purposes in 2009/10.
- There may be timing differences between when investment is undertaken for tax purposes, and when it is undertaken for the purposes of the Capex Survey. This might be particularly problematic given the use of quarterly data.
Turning now to the different responses of incorporated and unincorporated businesses, the results from estimating the model separately for each business structure are in Table 7. They suggest that a 10 percentage point increase in the tax break leads to an increase in company investment of 12 per cent and an increase in unincorporated business investment of around 60 per cent. The p-value from a test of the equality of these coefficients is less than 1 per cent. This result aligns with our priors regarding the effects of dividend imputation.
| Companies | Unincorporated businesses (sole traders and partnerships) |
|
|---|---|---|
| η | 1.13*** (0.38) |
4.89*** (1.27) |
| Clusters (businesses) | 3,415 | 908 |
| Observations | 8,783 | 1,862 |
|
Notes: Control group is businesses of the same legal type with revenue $2–10 million; *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the business level |
||
The estimated semi-elasticity for unincorporated businesses is broadly in line with estimates for small US companies in ZM (around 6.3). This is consistent with the fact that the US tax system does not allow for dividend imputation, and so is more comparable to the tax arrangements available to the owners of unincorporated businesses in Australia.
Interestingly, the estimate for companies is higher than the pooled estimate from above. Given the differing elasticities, this is not entirely surprising: large unincorporated businesses would be a poor control group for small companies, as they would respond quite strongly even to the 10 per cent tax break. Nevertheless, the estimated semi-elasticity for companies remains below the range estimated by the RD model.
Finally, Table 8 shows the results from the extensive margin model. The results indicate that a 10 percentage point increase in the tax break rate increases the odds of a business investing by 4 per cent. The average probability of a small business investing in a non-treatment quarter is 16 per cent, so the 50 per cent deduction for small businesses would raise the probability of investing to about 20 per cent. Again, the estimated effect is a bit larger when we use the broader control group.
As with the RD model, we can also examine whether businesses brought forward investment. We do this by including lags of the tax credit one and two years prior to the current quarter. If businesses simply brought forward investment, the coefficients on these variables should be negative and significant, as earlier higher levels of tax breaks should induce lower current investment. We focus on the intensive margin and find no evidence of statistically or economically significant intertemporal substitution of this type (Table 9).
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 0.43*** (0.01) |
1.10*** (0.02) |
| Clusters (ANZSIC division) | 14 | 14 |
| Business fixed effects | Yes | Yes |
| Observations | 61,210 | 117,759 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the industry level |
||
| Control group – $2–10 million | ||
|---|---|---|
| One lag of tax break | Two lags of tax break | |
| η | 0.87*** (0.31) |
0.96*** (0.32) |
| Tax break lagged one year | −0.36 (0.28) |
−0.25 (0.29) |
| Tax break lagged two years | 0.26 (0.30) |
|
| Clusters (businesses) | 5,724 | 5,724 |
| Business fixed effects | Yes | Yes |
| Observations | 14,379 | 14,379 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the business level |
||
6.3 Placebo Test
The Capex Survey dataset also provides information on building capex. As this type of capital expenditure was not covered by the investment tax break, it provides a natural setting for a placebo test of our DD strategy. If the parallel trends assumption is valid, equipment investment would have evolved similarly for the control and treatment groups in the absence of the tax break. As the tax break did not apply to building investment, this should still be the case even with the tax break. So re-running the model with building investment as the dependent variable should lead to estimates close to zero if the parallel trends assumption is valid.
Table 10 contains results for the baseline intensive margin model with building capex as the left-hand side variable. With the baseline control group, the response of building capex is close to zero. With the broader control group the response is larger, but is not statistically significant. A version of this model that includes equipment investment on the right-hand side – to control for potential complementarities or substitutability – provides similar results. This placebo test provides support for the parallel trends assumption, particularly for the narrow control group.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | 0.03 (1.03) |
0.56 (0.64) |
| Clusters (businesses) | 1,603 | 4,296 |
| Business fixed effects | Yes | Yes |
| Observations | 2,639 | 16,427 |
|
Note: Standard errors are in parentheses and are clustered at the business level |
||
The extensive margin placebo test has different results (Table 11). It indicates that small businesses, who received the largest tax breaks, were less likely to invest in buildings during the period in which the tax breaks were in place. One explanation could be that equipment and building investment are substitutes along the extensive margin. We try to account for this by including a variable that indicates whether or not businesses invested in equipment. However, when we do so the results suggest that building and equipment investment are, in fact, complements, and the estimate of η remains largely unchanged. It is still possible that the short-lived nature of the tax breaks caused building and equipment investment to become substitutes during the relevant period. But this seems unlikely given there is no evidence of such a change in the intensive margin placebo test.
| Control group | ||
|---|---|---|
| $2–10 million | > $2 million | |
| η | −0.69*** (0.03) |
−0.09*** (0.02) |
| Clusters (division) | 14 | 14 |
| Business fixed effects | Yes | Yes |
| Observations | 61,210 | 118,548 |
|
Notes: *** indicates significance at 1 per cent level; standard errors are in parentheses and are clustered at the division level |
||
The more likely explanation is that the parallel trends assumption does not hold for the extensive margin. It is plausible that this breach relates specifically to building investment, in which case it has no implications for our earlier results. For example, tighter borrowing conditions for small businesses may have affected building investment more than equipment investment due to the larger and lumpier nature of building investment. But, if it relates to both building and equipment investment, it indicates that our earlier results for the extensive margin were biased down and so understate the effect of the tax break.
6.4 Heterogeneous Responses by Business Size
ZM provide evidence that η is negatively correlated with business size – that is, small businesses respond more strongly to tax breaks. We analyse this by providing estimates from DD models that use different ranges of business size as the control group (Table 12). If the tax semi-elasticity for larger control groups is lower, estimates of η should increase with the size of the control group.
This is because the estimates should be increasingly upwardly biased, as the treatment group would be responding more than the control group to the 10 per cent tax break, even in the absence of the additional 40 percentage point tax break (the treatment). This exercise uses data for companies only, in order to abstract from differences across business legal types, and concentrates on the intensive margin.
| Control group | ||||||
|---|---|---|---|---|---|---|
| $2–10 million | $10–50 million | $50–100 million | $100–500 million | $500 million–$1 billion | > $1 billion | |
| η | 1.13*** (0.38) |
1.50*** (0.31) |
1.52*** (0.33) |
1.83*** (0.30) |
1.66*** (0.37) |
1.67*** (0.37) |
| Clusters (companies) | 3,415 | 4,337 | 3,441 | 3,872 | 2,662 | 2,500 |
| Company fixed effects | Yes | Yes | Yes | Yes | Yes | Yes |
| Observations | 8,783 | 14,434 | 11,254 | 19,178 | 8,572 | 8,211 |
|
Notes: *** indicates significance at the 1 per cent level; standard errors are in parentheses and are clustered at the company level |
||||||
Estimated elasticities rise with the size of the control group used, up to around $500 million in revenue. However, the confidence intervals for most of the estimates overlap, suggesting that the coefficients cannot be statistically distinguished. So these results are somewhat consistent with the size heterogeneity found by ZM.[23]
The results of this exercise should be treated with caution. This is because it is unclear whether the differences in estimated semi-elasticities reflect differing elasticities, or other differences in economic and financial conditions between businesses of different sizes. The latter would likely bias our estimates downwards given most plausible trends in small and large business conditions during the GFC involve worse conditions for small businesses. For example, credit spreads for business lending rose during 2009, but by more for small businesses than for large (e.g. Hambur and La Cava 2018). Both the fact that these larger control groups pass placebo tests using building investment, and the fact that the estimated elasticities rise with business size, suggest the former explanation. In either case, the results support our choice to limit the baseline control group to businesses with revenue to $10 million.
6.5 Macroeconomic Effect
The estimated elasticity of aggregate equipment investment to the tax break can be used to calculate its macroeconomic effects. This elasticity can be obtained from a model using investment data aggregated to the division-by-business size level using sample weights provided by the ABS (see Appendix C for these results). This aggregation allows us to abstract from the separate effects of the tax break on businesses' investment at the extensive and intensive margins.[24]
We take the semi-elasticity estimated using businesses with revenue to $10 million as the control group to be our ‘true’ elasticity for all businesses with revenue less than $10 million. This elasticity is 1.76. Given the above evidence, we apply a lower elasticity to larger businesses using an ad hoc approach. We calculate this based on the difference between the estimated elasticity using the baseline control group, and that estimated using larger control groups. Specifically, we use the following formula: 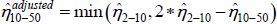 (e.g. for the $10 million to $50 million group). This formula restricts elasticities for the larger groups to be less than or equal to that for the baseline control group. In theory this method allows zero or negative elasticities for larger groups, if the results from the regressions with the control groups indicate that this is warranted. In practice, the adjusted elasticities range from 0.88–1.76.
(e.g. for the $10 million to $50 million group). This formula restricts elasticities for the larger groups to be less than or equal to that for the baseline control group. In theory this method allows zero or negative elasticities for larger groups, if the results from the regressions with the control groups indicate that this is warranted. In practice, the adjusted elasticities range from 0.88–1.76.
Applying these elasticities, we calculate that non-mining equipment capex would have been 29 per cent lower in 2009 if the investment tax break had not been in place. It is illustrative to translate this share of non-mining equipment capex into shares of other macroeconomic aggregates. Real private equipment investment in 2009 was $75.2 billion, and 29 per cent of this is $21.8 billion. If we adjust this down to account for the fact that around 25 per cent of investment in Australia is done using imported goods (Bussière et al 2013) and remove the remainder from 2009 real GDP, it implies year-average growth over 2009 of 0.5 per cent, well below actual growth of 1.7 per cent.[25] If this exercise is performed on a quarterly basis, real GDP declines in the March and June quarters of 2009 (actual GDP fell only in the December quarter of 2008). Using different elasticities for companies and unincorporated businesses (as well as size) changes this result only slightly. Using the elasticity from the RD model would massively increase the estimated effect of the tax break. But, given the estimate is very ‘local’, doing so seems inappropriate when estimating aggregate effects.
The above are partial equilibrium estimates. They do not account for other changes in the economy that would have occurred as a result of lower investment. If general equilibrium responses were included, it is likely that the reduction in GDP growth would be significantly smaller. Such general equilibrium responses include lower interest rates from a likely easing of monetary policy.
To account for general equilibrium effects, we use the dynamic stochastic general equilibrium model laid out in Gibbs, Hambur and Nodari (2018).[26] Without the additional investment induced by the tax break, adjusted down for the import share, the model suggests that year-ended GDP growth over 2009 would have been 0.8 per cent. In part, the smaller decline in GDP in this general equilibrium setting reflects additional monetary easing, with the model predicting that the cash rate would have been about 50 basis points lower in the absence of the investment tax break.
Footnotes
So it is log 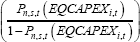 . The four granular turnover categories are those shown in Figure 7.
[20]
. The four granular turnover categories are those shown in Figure 7.
[20]
The variable is equivalent to the discounted cash flow measure used in ZM, given that for the Australian investment tax break the full tax benefit accrues in the first year. [21]
The regressions are unweighted, so we are effectively treating the responses underlying the Capex Survey as a simple random sample. Weighted regressions that use the Capex Survey sample weights, and models that exclude the large businesses that are always selected into the sample, generate similar results. [22]
An interesting feature of the results is that the estimated semi-elasticities actually decline for very large companies – with revenue above $500 million – indicating that these companies responded more strongly to the tax breaks than companies with revenue of $100 to $500 million. This is consistent with very large companies having more foreign investors, and therefore a lower γ in their user cost, making their costs of capital more sensitive to the tax break. [23]
While these aggregate results indicate that building and equipment investment are complements, we abstract from any potential positive spillovers to building investment in this analysis. [24]
Equipment investment is likely to be more import-intensive than other types of investment, such as non-residential construction. As such, the adjustment we make is probably too small, and so the effects of the tax break are likely to be a bit overstated. [25]
The approach suggested in Sraer and Thesmar (2018) offers another potential way forward here. [26]