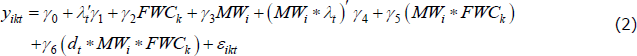RDP 2018-06: The Effect of Minimum Wage Increases on Wages, Hours Worked and Job Loss 7. Results
May 2018
- Download the Paper 1,216KB
7.1 Baseline Estimates
The baseline estimates for wages, hours worked and the job destruction rate are shown in Table 2. I present separate estimates using the full sample and a sample that omits the first four FWC decisions (1998–2001). Although the sample size is larger for the full sample, there is a data issue prior to 2002 that could potentially distort the regression results.[9]
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| 1998–2008 sample | 0.84*** (0.03) |
0.26 (0.37) |
−0.22 (0.44) |
| 2002–08 sample | 0.93*** (0.04) |
0.13 (0.47) |
−0.37 (0.55) |
| Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively | |||
I find strong evidence that award adjustments are passed on to wages. Using the full sample, I estimate the elasticity of wages with respect to the award wage to be 0.84 and highly statistically significant.[10] This estimate is larger in the shorter sample period – 0.93 – which suggests that measurement issues in the first few years of data may be attenuating the size of the overall elasticity in the full sample.[11] The results suggest less-than-full pass-through of FWC decisions to wages. The hypothesis that the wage elasticity is equal to one can be rejected at the 1 and 10 per cent levels of significance using the 1998–2008 and 2002–08 samples, respectively. This may reflect some degree of non-compliance by firms in their legal obligations (see Productivity Commission (2015a, p 12) for a discussion), or simply measurement error. In any case, the elasticity is sufficiently close to one to characterise this as near-complete pass-through.
Having established that award wage increases are passed through to wages, the next step is to see if this leads to any reductions in hours worked or job loss. I find no evidence that award changes have an adverse effect on hours worked (Table 2).[12] In fact, the DD estimate is positive, suggesting that jobs with larger award wage rises had larger increases in hours worked than jobs experiencing a smaller award wage rise. Based on the 95 per cent confidence interval, I am able to rule out adverse effects on hours worked that are larger (in absolute value) than −0.46.[13] I also find that award wage increases do not have a statistically significant effect on the job destruction rate (Table 2). Again, if anything, the point estimates suggest that the job destruction rate actually declines when the award wage is increased.
7.2 Difference-in-difference-in-differences
Like any analysis using difference-in-differences, my results are sensitive to violations of the so called ‘parallel trends’ assumption. The assumption is that in the absence of a change in award wages, the wages, hours worked and probability of job loss of low-award-wage workers would have followed the same trajectory as high-award-wage workers. This would be violated if, say, there is a change in tax policy that affects low-wage earners relatively more than high-wage earners that occurs at the same time as the change in award wages. If this happens, we may incorrectly attribute the effect of the tax change to the award wage. This assumption is often examined by looking at pre-treatment trends across the treatment and control groups. I do not have sufficient pre-treatment data to allow me to perform such a test.
Instead, I implement a difference-in-difference-in-differences (DDD) approach to address any concerns about violations of the parallel trends assumption. The idea of this approach is to use low- and high-wage jobs whose wages are set according to enterprise bargaining agreements (EBAs) as an additional control group. These jobs are paid wages above the legal minima that are contractually ‘locked-in’ for a specified period of time, and thus are not affected by the award wage decisions.[14]
Conceptually, this DDD approach involves estimating a separate DD model using jobs whose pay is set by an EBA. The wage levels of these jobs are used to infer what wage adjustment they would have had had their pay been set by an award (this is the size of the ‘treatment’ experienced by this group). I then subtract these estimates from the baseline DD estimates to adjust the latter for any shocks that differentially affect low-wage jobs. For example, say there is a shock in the after period that only affects low-wage jobs. The baseline DD estimates will be biased. However, if the shock has the same effect on the low-wage jobs on EBAs, then the DDD model will fully absorb the effect of that shock. The DDD specification is as follows,
where MWi is a dummy variable that equals one if the job's pay is set according to an award, and zero otherwise (the base category is jobs whose pay is set according to an EBA). The coefficient of interest is the coefficient on the third-level interaction (γ6), which provides the DDD estimate of the effect of a change in award wages on the outcome variable yikt for award-reliant jobs. The model is estimated on the combined sample of jobs paid an award and jobs covered by EBAs.
The results suggest that the baseline estimates are robust to controlling for violations of the parallel trends assumption (Table 3). For wages, the DD estimates for the EBA sample are close to zero and hence the results of the DDD model are very similar to the baseline DD model. The fact that award wage decisions do not spill over to jobs on EBAs suggests that the baseline estimates for wages are not being driven by wage group-specific shocks. It also indicates that jobs on EBAs are an appropriate control group. The results for hours worked and the job destruction rate are also robust to controlling for wage growth-specific shocks using the DDD model.
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| 1998–2008 sample | |||
| (A) DD for awards | 0.84*** (0.03) |
0.26 (0.37) |
−0.22 (0.44) |
| (B) DD for EBAs | 0.03 (0.02) |
0.09 (0.21) |
0.14 (0.24) |
| (A – B) DDD | 0.81*** (0.03) |
0.17 (0.42) |
−0.36 (0.50) |
| 2002–08 sample | |||
| (A) DD for awards | 0.93*** (0.04) |
0.13 (0.47) |
−0.37 (0.55) |
| (B) DD for EBAs | 0.01 (0.02) |
0.01 (0.24) |
0.35 (0.27) |
| (A – B) DDD | 0.92*** (0.04) |
0.12 (0.53) |
−0.72 (0.61) |
|
Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively |
|||
7.3 Placebo Test
Another way to assess the validity of the parallel trends assumption is to do a placebo test using the FWC decision that immediately followed our estimation period of 1998–2008. In 2009, the FWC unexpectedly froze all minimum and award wages due to concerns about rising unemployment during the global financial crisis. Because there was no change in award wages in this decision, finding evidence of a casual effect on other labour market variables may indicate misspecification. I generate a ‘placebo treatment’ by assuming that the FWC had actually granted a flat increase of 57 cents per hour in 2009, which was the size of the increase in 2008. I find no evidence of any placebo effect when estimating the DDD model for the 2009 FWC decision (Table 4). This provides added confidence that the parallel trends assumption is valid.
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| (A) DD for awards | −0.22* (0.12) |
−0.06 (1.76) |
3.04* (1.66) |
| (B) DD for EBAs | −0.22*** (0.05) |
0.58 (0.85) |
2.59*** (0.74) |
| (A – B) DDD | 0.01 (0.13) |
0.64 (1.95) |
0.44 (1.84) |
| Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively | |||
7.4 Constant Elasticity Assumption
The interpretation of the results in Tables 2 and 3 as causal effects assumes that the elasticities of hours worked and job loss with respect to the minimum wage are constant throughout the distribution of skills. Some studies find that the employment of lower-skilled workers is more sensitive to minimum wage changes than higher-skilled workers (Gindling and Terrell 2007). If this were true, it would bias us toward estimating employment effects that are larger (i.e. more adverse) than the ‘true’ effect. Given that I found no discernible effect of award wages on hours worked or the job destruction rate, the likely sign of the bias reinforces the conclusion that award wage increases do not have large adverse employment effects.
Footnotes
This data issue relates to the fact that I cannot perfectly observe whether a job was paid according to an award prior to 2002. For this period, I could only identify the job's pay-setting mechanism (e.g. award or enterprise bargaining agreement) using procedures such as text searches for relevant keywords in the job-level data, which can be error-prone. After 2002, the pay-setting mechanism was explicitly coded in the dataset and therefore measured with less error. [9]
Clustering standard errors at the individual job level produced standard errors that were more conservative than clustering at the wage group level. [10]
These estimates are slightly higher than those found for the United States. For example, Neumark, Schweitzer and Wascher (2004) estimate that the short-run elasticity of minimum-wage workers' hourly wages with respect to the US minimum wage is 0.8. [11]
Due to a number of extreme values for log changes in average hours worked, I exclude any jobs with a log change greater than 4 standard deviations away from the sample mean. My estimates are not sensitive to this decision. [12]
Although these estimates do not capture any effect of award wage changes on overtime hours worked (since the hours worked variable only includes ordinary-time hours), I also find no effect of award wage changes on the probability that the job occupant worked any paid overtime hours during the survey period. This is modelled using a binary dependent variable that equals one if the occupant of the job received an overtime payment in the last full pay period prior to the WPI survey date, and zero otherwise (conditional on the job being active in the quarter). [13]
I exclude any jobs whose EBA includes an automatic adjustment to FWC decisions, because such EBAs are not a valid control group. I am able to identify such agreements in the data since the WPI survey collects information on the source(s) of any change in wages between consecutive quarterly surveys. I exclude from the EBA sample any job that ever listed an FWC decision as a reason for a pay adjustment. This comprises around one-fifth of all EBA jobs in the survey. [14]