RDP 2017-01: Gauging the Uncertainty of the Economic Outlook Using Historical Forecasting Errors: The Federal Reserve's Approach 6. Estimation Results
February 2017
We now turn to estimates of the historical accuracy of the various forecasters in our panel over the past twenty years. Tables 2 through 5 report the root mean squared errors of each forecaster's predictions of real activity, inflation, and short-term interest rates from 1996 through 2015, broken down by the quarter of the year in which the forecast was made and the horizon of the forecast expressed in terms of current-year projection, one-year-ahead projection, and so forth. Several key results emerge from a perusal of these tables.
| RMSEs for predictions of conditions in: | ||||
|---|---|---|---|---|
| Current year | Next year | Two years ahead | Three years ahead | |
| First-quarter projections | ||||
| Federal Open Market Committee | 1.63 | |||
| Federal Reserve Board staff | 1.54 | 2.20 | ||
| Administration | ||||
| Congressional Budget Office | 1.69 | 2.15 | 2.14(a) | 2.18(a) |
| Blue Chip | 1.59 | 2.03 | 1.96(a) | 1.88(a) |
| Survey of Professional Forecasters | 1.63 | 1.87(a) | ||
| Average | 1.62 | 2.13(b) | 2.05 | 2.03 |
| Second-quarter projections | ||||
| Federal Open Market Committee | 1.40 | 2.02 | ||
| Federal Reserve Board staff | 1.35 | 2.06 | ||
| Administration | 1.45 | 2.13 | 2.19 | 2.15 |
| Congressional Budget Office | ||||
| Blue Chip | 1.37 | 1.99 | ||
| Survey of Professional Forecasters | 1.43 | 1.77(a) | ||
| Average | 1.40 | 2.06(b) | 2.19 | 2.15 |
| Third-quarter projections | ||||
| Federal Open Market Committee | ||||
| Federal Reserve Board staff | 1.19 | 1.93 | 2.18 | |
| Administration | ||||
| Congressional Budget Office | 1.35 | 2.07 | 2.11(a) | 2.27(a) |
| Blue Chip | 1.23 | 1.89 | 1.97(a) | 1.93(a) |
| Survey of Professional Forecasters | 1.26 | 1.58(a) | ||
| Average | 1.26 | 1.96(b) | 2.05 | 2.10 |
| Fourth-quarter projections | ||||
| Federal Open Market Committee | ||||
| Federal Reserve Board staff | 0.79 | 1.75 | 2.24 | |
| Administration | 0.88 | 1.84 | 2.16 | 2.19 |
| Congressional Budget Office | ||||
| Blue Chip | 0.89 | 1.68 | ||
| Survey of Professional Forecasters | 0.95 | 1.76 | ||
| Average | 0.88 | 1.75 | 2.20 | 2.19 |
|
Notes: Actual real GDP is defined using the historical estimates published by the Bureau of Economic Analysis in April 2016, adjusted for selected methodological and definitional changes to the series over time; unless otherwise noted, growth prediction errors refer to percent changes, fourth quarter of year from fourth quarter of previous year (a) Percent change, annual average for year relative to annual average of
previous year |
||||
| RMSEs for predictions of conditions in: | ||||
|---|---|---|---|---|
| Current year | Next year | Two years ahead | Three years ahead | |
| First-quarter projections | ||||
| Federal Open Market Committee | 0.61 | |||
| Federal Reserve Board staff | 0.41 | 1.24 | ||
| Administration | ||||
| Congressional Budget Office | 0.46(a) | 1.24(a) | 1.77(a) | 1.96(a) |
| Blue Chip | 0.51 | 1.35 | 1.72(a) | 2.00(a) |
| Survey of Professional Forecasters | 0.57 | 1.14(a) | ||
| Average | 1.53(b) | 1.29(c) | 1.74 | 1.98 |
| Second-quarter projections | ||||
| Federal Open Market Committee | 0.37 | 1.24 | ||
| Federal Reserve Board staff | 0.36 | 1.22 | ||
| Administration | 0.40 | 1.28 | 1.80 | 2.01 |
| Congressional Budget Office | ||||
| Blue Chip | 0.39 | 1.27 | ||
| Survey of Professional Forecasters | 0.42 | 1.02(a) | ||
| Average | 0.39 | 1.26(d) | 1.80 | 2.01 |
| Third-quarter projections | ||||
| Federal Open Market Committee | ||||
| Federal Reserve Board staff | 0.27 | 1.12 | 1.69 | |
| Administration | ||||
| Congressional Budget Office | 0.19(a) | 1.02(a) | 1.67(a) | 2.00(a) |
| Blue Chip | 0.33 | 1.15 | 1.53(a) | 1.92(a) |
| Survey of Professional Forecasters | 0.34 | 0.91(a) | ||
| Average | 0.31(b) | 1.14(c) | 1.63 | 1.96 |
| Fourth-quarter projections | ||||
| Federal Open Market Committee | ||||
| Federal Reserve Board staff | 0.11 | 0.75 | 1.45 | |
| Administration | 0.14 | 0.80 | 1.54 | 1.90 |
| Congressional Budget Office | ||||
| Blue Chip | 0.13 | 0.79 | ||
| Survey of Professional Forecasters | 0.15 | 0.87 | ||
| Average | 0.13 | 0.80 | 1.49 | 1.90 |
|
Notes: Actual unemployment rate is defined using the historical estimates published by the Bureau of Labor Statistics in April 2016; unless otherwise noted, prediction errors refer to fourth-quarter averages, in percent (a) Annual average |
||||
| RMSEs for predictions of conditions in: | ||||
|---|---|---|---|---|
| Current year | Next year | Two years ahead | Three years ahead | |
| First-quarter projections | ||||
| Federal Reserve Board staff | 0.87 | 1.16 | ||
| Administration | ||||
| Congressional Budget Office | 0.98 | 1.10 | 1.11(a) | 1.02(a) |
| Blue Chip | 0.86 | 0.99 | 1.12(a) | 1.12(a) |
| Survey of Professional Forecasters | 0.94 | 0.99 | ||
| Average | 0.91 | 1.06 | 1.12 | 1.07 |
| Second-quarter projections | ||||
| Federal Reserve Board staff | 0.90 | 1.12 | ||
| Administration | 0.69 | 0.99 | 1.04 | 0.98 |
| Congressional Budget Office | ||||
| Blue Chip | 0.71 | 1.02 | ||
| Survey of Professional Forecasters | 0.72 | 1.01 | ||
| Average | 0.75 | 1.04 | 1.04 | 0.98 |
| Third-quarter projections | ||||
| Federal Reserve Board staff | 0.63 | 1.12 | 1.17 | |
| Administration | ||||
| Congressional Budget Office | 0.95 | 1.08 | 1.16(a) | 1.07(a) |
| Blue Chip | 0.80 | 1.01 | 1.11(a) | 1.11(a) |
| Survey of Professional Forecasters | 0.81 | 1.00 | ||
| Average | 0.80 | 1.05 | 1.15 | 1.09 |
| Fourth-quarter projections | ||||
| Federal Reserve Board staff | 0.07 | 1.03 | 1.10 | |
| Administration | 0.15 | 0.99 | 1.03 | 1.02 |
| Congressional Budget Office | ||||
| Blue Chip | 0.27 | 0.94 | ||
| Survey of Professional Forecasters | 0.47 | 0.95 | ||
| Average | 0.24 | 0.98 | 1.07 | 1.02 |
|
Notes: Actual CPI inflation is defined using the historical estimates published by the Bureau of Labor Statistics in April 2016; unless otherwise noted, growth prediction errors refer to percent changes, fourth quarter of year from fourth quarter of previous year (a) Percent change, annual average for year relative to annual average of previous year |
||||
| RMSEs for predictions of conditions in: | ||||
|---|---|---|---|---|
| Current year | Next year | Two years ahead | Three years ahead | |
| First-quarter projections | ||||
| Federal Reserve Board staff | 0.84 | 1.94 | ||
| Administration | ||||
| Congressional Budget Office | 0.58(a) | 1.78(a) | 2.33(a) | 2.73(a) |
| Blue Chip | 0.92 | 2.09 | 2.49(a) | 2.86(a) |
| Survey of Professional Forecasters | 0.97 | 1.62(a) | ||
| Average | 0.91(b) | 2.02(c) | 2.41 | 2.80 |
| Second-quarter projections | ||||
| Federal Reserve Board staff | 0.68 | 1.90 | ||
| Administration | 0.22(a) | 1.48(a) | 2.22(a) | 2.67(a) |
| Congressional Budget Office | ||||
| Blue Chip | 0.74 | 2.00 | ||
| Survey of Professional Forecasters | 0.74 | 1.50(a) | ||
| Average | 0.72(b) | 1.95(c) | 2.22 | 2.67 |
| Third-quarter projections | ||||
| Federal Reserve Board staff | 0.41 | 1.64 | 2.31 | |
| Administration | ||||
| Congressional Budget Office | 0.22(a) | 1.44(a) | 2.24(a) | 2.60(a) |
| Blue Chip | 0.58 | 1.74 | 2.09(a) | 2.66(a) |
| Survey of Professional Forecasters | 0.62 | 1.28(a) | ||
| Average | 0.54(b) | 1.69(c) | 2.21 | 2.63 |
| Fourth-quarter projections | ||||
| Federal Reserve Board staff | 0.06 | 1.38 | 2.07 | |
| Administration | 0.04(a) | 0.86(a) | 1.81(a) | 2.41(a) |
| Congressional Budget Office | ||||
| Blue Chip | 0.10 | 1.37 | ||
| Survey of Professional Forecasters | 0.17 | 1.44 | ||
| Average | 0.11(b) | 1.40(b) | 1.94 | 2.41 |
|
Notes: Unless otherwise noted, growth prediction errors refer to fourth-quarter averages, in percent (a) Annual average |
||||
6.1 Differences in Forecasting Accuracy are Small
One key result is that differences in accuracy across forecasters are small. For almost all variable-horizon combinations for which forecasts are made on a comparable basis – for example, projections for the average value of the unemployment rate in the fourth quarter – root mean squared errors typically differ by only one or two tenths of a percentage point across forecasters, controlling for release date. Compared with the size of the RMSEs themselves, such differences seem relatively unimportant.
Moreover, some of the differences shown in the tables probably reflect random noise, especially given the small size of our sample. To explore this possibility, Table 6 reports p-values from tests of the hypothesis that all forecasters have the same predictive accuracy for a specific series at a given horizon – that is, the likelihood of seeing the observed differences in predicted performance solely because of random sampling variability. These tests are based on a generalization of the Diebold and Mariano (1995) test of predictive accuracy, and include all forecast errors made by our panelists of economic conditions over the period 1984 to 2015.[24] In almost 90 percent of the various release-variable-horizon combinations, p-values are greater than 5 percent, usually by a wide margin. Moreover, many of the other combinations concern the very short-horizon current-year forecasts, where the Federal Reserve staff has the lowest RMSEs for reasons that may reflect a timing advantage. For example, the Tealbook's fourth quarter forecasts are usually finalized in mid-December, late enough to allow them to take on board most of the Q4 data on interest rates, the October CPI releases and November labor market reports, in contrast to the SPF and, in some years, the CEA and the Blue Chip projections. Similar advantages apply at longer horizons, though they quickly become unimportant. Overall, these results seem consistent with the view that, for practical purposes, the forecasters in our panel are equally accurate.[25]
| Projections of conditions in the: | ||||
|---|---|---|---|---|
| Current year | Second year | Third year | Fourth year | |
| First-quarter projections | ||||
| Real GDP | 0.80 | 0.69(c) | 0.06 | 0.06 |
| Unemployment rate | 0.07(a) | 0.37(a),(c) | 0.47 | 0.40 |
| Total CPI | 0.16 | 0.61 | 0.15 | 0.06 |
| Treasury bill rate | 0.71(a) | 0.90(a),(c) | 0.07 | 0.05 |
| Second-quarter projections | ||||
| Real GDP | 0.87 | 0.65(c) | ||
| Unemployment rate | 0.67 | 0.48(c) | ||
| Total CPI | 0.75 | 0.67 | ||
| Treasury bill rate | 0.34(b) | 0.15(c) | ||
| Third-quarter projections | ||||
| Real GDP | 0.50 | 0.74(c) | 0.87 | 0.07 |
| Unemployment rate | 0.14(a) | 0.40(a),(c) | 0.29 | 0.54 |
| Total CPI | <0.01 | 0.52 | 0.96 | 0.16 |
| Treasury bill rate | 0.04(a) | 0.18(a),(c) | 0.36 | 0.18 |
| Fourth-quarter projections | ||||
| Real GDP | 0.05 | 0.82 | 0.67 | |
| Unemployment rate | 0.01 | 0.02 | 0.09 | |
| Total CPI | <0.01 | 0.87 | 0.39 | |
| Treasury bill rate | 0.02(b) | 0.07 | 0.04 | |
|
Notes: p-values are derived from a multivariate generalization of the Diebold and Mariano (1995) test of predictive accuracy; details are presented in footnote 24 (a) Excludes CBO annual-average forecasts |
||||
This conclusion also seems warranted given the tendency for forecasters to make similar individual prediction errors over time – a phenomenon that both Gavin and Mandal (2001) and Sims (2002) have noted. This tendency reveals itself in correlations that typically range from 0.85 to 0.98 between prediction errors made on a comparable release, horizon, and measurement basis for the different forecasters in our panel. That forecasters make similar mistakes does not seem surprising. All forecasters use the past as a guide to the future, and so any deviation from average historical behavior in the way the economy responds to a shock will tend to result in common projection errors. Moreover, such apparent deviations from past behavior are not rare, both because our understanding of the economy is limited, and because shocks never repeat themselves exactly. Finally, some economic disturbances are probably inherently difficult to predict in advance, abstracting from whether forecasters clearly understand their economic consequences once they occur. Based on these considerations, it is not surprising that highly correlated prediction errors would result from such events as the pick-up in productivity growth that occurred in the late 1990s and the recent financial crisis.
Our overall conclusion from these results is that all forecasters, including the Federal Reserve Board staff, have been equally accurate in their predictions of economic conditions over the past twenty years, a finding that somewhat conflicts with other studies.[26] This similarity has important implications for the SEP methodology because it means that errors made by other forecasters can be assumed to be representative of those that might be made by the FOMC.
6.2 RMSE Statistics Show that Uncertainty is Large
Tables 2 through 5 also report ‘benchmark’ measures of uncertainty of the sort reported in the Summary of Economic Projections. These benchmarks are calculated by averaging across the individual historical RMSEs of the forecasters in our panel for the period 1996 to 2015, controlling for publication quarter and horizon. When only one source is available for a given publication quarter and horizon, that source's RMSE is used as the benchmark measure.[27]
These benchmark measures of uncertainty are also illustrated by the solid red lines in Figure 1, with the average RMSE benchmarks now reported on a k-quarter-ahead basis. For example, the zero-quarter-ahead benchmark for real GDP growth is the average RMSE reported in Table 2 for current-year GDP forecasts published in the fourth quarter, the one-quarter-ahead benchmark is the average RMSE for current-year forecasts published in the third quarter, and so on through the fifteen-quarters-ahead benchmark, equal to the average RMSE for three-year-ahead GDP forecasts released during the first quarter. (For convenience, Table 1B reports the sub-samples of forecasters whose errors are used to compute RMSEs and other statistics at each horizon.)
Historical Root Mean Squared Prediction Errors Averaged Across Forecasters
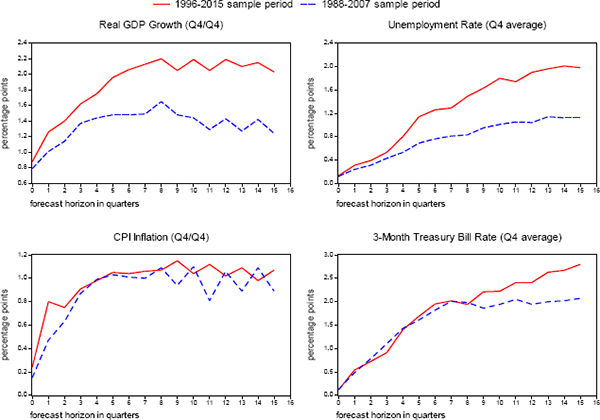
Source: Authors' calculations, using data published by the Bureau of Labor Statistics, the Bureau of Economic Analysis, and the Federal Reserve Board, and forecasts made by the Federal Open Market Committee, the staff of the Federal Reserve Board, the Congressional Budget Office, the Administration, and private forecasters as reported in the Survey of Professional Forecasters and Blue Chip Economic Indicators.
As can be seen, the accuracy of predictions for real activity, inflation, and short-term interest rates deteriorates as the length of the forecast horizon increases. In the case of CPI inflation, the deterioration is limited and benchmark RMSEs level out at roughly 1 percentage point for forecast horizons of more than four quarters; benchmark uncertainty for real GDP forecasts also level out over the forecast horizon at about 2 percentage points. In the case of the unemployment rate and the 3-month Treasury bill rate, predictive accuracy deteriorates steadily with the length of the forecast horizon, with RMSEs eventually reaching 2 percentage points and 2¾ percentage points, respectively. There are some quarter-to-quarter variations in the RMSEs – for example, the deterioration in accuracy in current-year inflation forecasts from the second quarter to the third – which do not occur in earlier samples, and thus are likely attributable to sampling variability.
Average forecast errors of this magnitude are large and economically important. Suppose, for example, that the unemployment rate was projected to remain near 5 percent over the next few years, accompanied by 2 percent inflation. Given the size of past errors, we should not be surprised to see the unemployment rate climb to 7 percent or fall to 3 percent because of unanticipated disturbances to the economy and other factors. Such differences in actual outcomes for real activity would imply very different states of public well-being and would likely have important implications for the stance of monetary policy. Similarly, it would not be at all surprising to see inflation as high as 3 percent or as low as 1 percent, and such outcomes could also have important ramifications for the appropriate level of the federal funds rate if it implied that inflation would continue to deviate substantially from 2 percent.
Forecast errors are also large relative to the actual variations in outcomes seen over history. From 1996 to 2015, the standard deviations of Q4/Q4 changes in real GDP and the CPI were 1.8 and 1.0 percentage points respectively. Standard deviations of Q4 levels of the unemployment rate and the Treasury bill rate were 1.8 and 2.2 percentage points, respectively. For each of these variables, RMSEs (shown in Figure 1 and Tables 2 to 5) are smaller than standard deviations at short horizons but larger at long horizons. This result implies that longer-horizon forecasts do not have predictive power, in the sense that they explain little if any of the variation in the historical data.[28] This striking finding – which has been documented for the SPF (Campbell 2007), the Tealbook (Tulip 2009), and forecasts for other large industrial economies (Vogel 2007) – has important implications for forecasting and policy which are beyond the scope of this paper. Moreover, the apparent greater ability of forecasters to predict economic conditions at shorter horizons is to some extent an artifact of data construction rather than less uncertainty about the future, in that near-horizon forecasts of real GDP growth and CPI inflation span some quarters for which the forecaster already has published quarterly data.
6.3 Uncertainty about PCE Inflation and the Funds Rate can be Inferred from Related Series
Another key assumption underlying the SEP methodology is that one can use historical prediction errors for CPI inflation and 3-month Treasury bill rates to accurately gauge the accuracy of forecasts for PCE inflation and the federal funds rate, which are unavailable at long enough forecast horizons for a sufficiently long period. Fortunately, this assumption seems quite reasonable given information from the Tealbook that allows for direct comparisons of the relative accuracy of forecasts of inflation and short-term interest rates that are made using the four different measures. As shown in the upper panel of Figure 2, Tealbook root mean squared prediction errors for CPI inflation over the past twenty years are only modestly higher than comparable RMSEs for PCE inflation, presumably reflecting the greater weight on volatile food and energy prices in the former. As for short-term interest rates, the lower panel reveals that Tealbook RMSEs for the Treasury bill rate and the federal funds rate are essentially identical at all forecast horizons. Accordingly, it seems reasonable to gauge the uncertainty of the outlook for the federal funds rate using the historical track record for predicting the Treasury bill rate, with the caveat that the FOMC's forecasts are expressed as each individual participant's assessment of the appropriate value of the federal funds rate on the last day of the year, not his or her expectation for the annual or fourth-quarter average value.
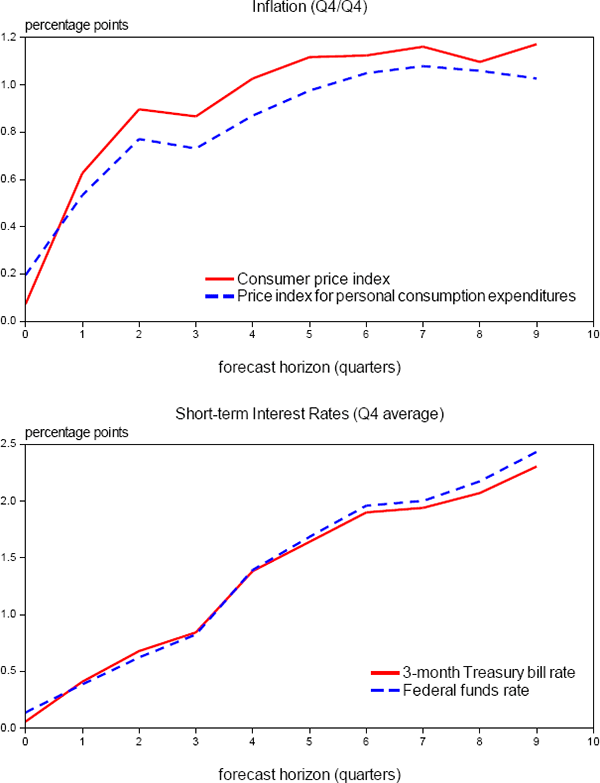
Source: Authors' calculations, using data published by the Bureau of Economic Analysis and the Federal Reserve Board, and forecasts made by the Federal Reserve Board staff.
6.4 Benchmark Estimates of Uncertainty are Sensitive to Sample Period
A key factor affecting the relevance of the FOMC's benchmarks is whether past forecasting performance provides a reasonable benchmark for gauging future accuracy. On this score, the evidence calls for caution. Estimates of uncertainty have changed substantially in the past. Campbell (2007) and Tulip (2009) report statistically and economically significant reductions in the size of forecast errors in the mid-1980s for the SPF and Tealbook, respectively.[29] More recently, RMSE's increased substantially following the global financial crisis, especially for real GDP growth and the unemployment rate. This is illustrated in Figure 1. The red solid line shows RMSEs for our current sample, 1996 to 2015, while the blue dashed line shows estimates for 1988 to 2007, approximately the sample period when the SEP first started reporting such estimates. Both sets of estimates are measured on a consistent basis, with the same data definitions.
One implication of these changes is that estimates of uncertainty would be substantially different if the sample period were shorter or longer. For example, our estimates implicitly assume that a financial crisis like that observed from 2007 to 2009 occur once every twenty years. If such large surprises were to occur less frequently, the estimated RMSEs would overstate the level of uncertainty. Another implication is that, because estimates of uncertainty have changed substantially in the past, they might be expected to do so again in the future. Hence there is a need to be alert to the possibility of structural change. Benchmarks need to be interpreted cautiously, and should be augmented with real-time monitoring of evolving risks, such as the FOMC's qualitative assessments.
Footnotes
In comparing two forecasts, one implements the test by regressing the difference between the squared errors for each forecast on a constant. The test statistic is a t-test of the hypothesis that the constant is significantly different from zero once allowance is made for the errors having a moving average structure. For comparing n forecasts, we construct n − 1 differences and jointly regress these on n − 1 constants. The test statistic that these constants jointly equal zero is asymptotically distributed chi-squared with n − 1 degrees of freedom, where again allowance is made for the errors following a moving average process. Forecasts that are excluded from the average RMSEs for comparability reasons (e.g., annual average forecasts for the unemployment rate and the Treasury bill rate) are not included in the tests. [24]
That the forecasts in our sample have similar accuracy is perhaps not surprising because everyone has access to basically the same information. Moreover, idiosyncratic differences across individual forecasters tend to wash out in our panel because the Blue Chip, SPF, and the FOMC projections reflect an average projection (mean, median or mid-point of a trimmed range) computed using the submissions of the various survey and Committee participants. The same ‘averaging’ logic may apply to the Tealbook, CEA, and CBO forecasts as well given that all reflect the combined analysis and judgment of many economists. [25]
Romer and Romer (2000) and Sims (2002) find that the Federal Reserve Board staff, over a period that extended back into the 1970s and ended in the early 1990s, significantly outperformed other forecasters, especially for short-horizon forecasts of inflation. Subsequent papers have further explored this difference. In contrast, a review of Tables 2 through 5 reveals that the Tealbook performs about the same as other forecasters for our sample, especially once its timing advantage, discussed above, is allowed for. It does better for some variables at some horizons, but not consistently or by much. [26]
In theory, the FOMC could have based the benchmark measures on the accuracy of hypothetical forecasts that could have been constructed at each point in the past by pooling the contemporaneous projections made by individual forecasters. In principle, such pooled projections could have been more accurate than the individual forecasts themselves, although it is an open question whether the improvement would be material. In any event, the FOMC's simpler averaging approach has the advantage of being easier to understand and hence more transparent. Another alternative, employed by the European Central Bank, would have been to use mean absolute errors in place of root mean squared errors, as the former have the potential advantage of reducing the influence of outliers in small samples. However, measuring uncertainty using root mean squared errors has statistical advantages (for example, it maps into a normal distribution and regression analysis), is standard practice, and may have the advantage of being more in line with the implicit loss function of policymakers and the public, given that large errors (of either sign) are likely viewed as disproportionately costly relative to small errors. [27]
This result implies that the sample mean would be more accurate than the forecast at longer horizons. Such an approach is not feasible because the sample mean is not known at the time the forecast is made, although Tulip (2009) obtains similar results using pre-projection-period means. [28]
For example, Tulip reports that the root mean squared error of the Tealbook forecast of real GDP growth was roughly 40 percent smaller after 1984 than before, while the RMSE for the GDP deflator fell by between a half and two-thirds. [29]