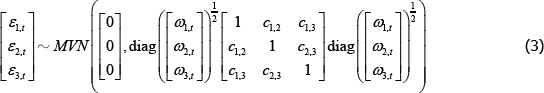RDP 2016-11: Identifying Interbank Loans from Payments Data 5. Features of the Market[27]
December 2016
- Download the Paper 3.19MB
With the most detailed IBOC market dataset ever constructed now at our disposal, we explore several features of the market that were previously unobservable. The results in this section both improve our understanding of how the market functions, and help to explain several of the changes that have occurred over the past decade.
With this paper being the first to identify rollovers, we start by determining the incidence of rollovers and whether rollovers and non-rolled loans exhibited different trends over the past decade (Section 5.1). Given that we find very different trends, we seek to determine whether rollovers and non-rolled loans are used for the same purpose and some reasons why they may not be perfect substitutes. We find that, while both loan types appear to be used to satisfy banks' late-day funding needs, the fact that rollovers are conducted earlier in the day (when banks may be less certain of their late-day funding requirements) is one reason why they may not be perfect substitutes (Sections 5.2 and 5.3).
We decompose the timing of IBOC market activity based on bank type, and determine whether the timing of banks' IBOC market activity has changed over the past decade (Section 5.2); we pay particular attention to the period following the introduction of same-day settlement of direct entry obligations. We find that banks are currently managing their end-of-day ESA balances during a briefer period (towards the end of the day) than has been the case historically.
We use regression techniques to determine when banks agree to a loan (as opposed to when it is settled in RITS; Section 5.3). Knowing agreement times is important for operational decisions made by the RBA. For example, the optimal timing of late-day open market operations depends on the timing of IBOC market activity. And it is important to know the periods during which a delay of high-value payments could affect the IBOC market.[28]
Finally, we decompose the changes in IBOC market activity into changes in the average size of loans and changes in the number of loans (Section 5.4; such a decomposition was not possible prior to the construction of our loan-level database). And we highlight the surprising fact that banks calculate the interest on rollovers using simple interest (as opposed to compounding), even though daily interest typically remained outstanding for the life of the rollover (Section 5.5).
5.1 Incidence of Rollovers
Rollovers appear to have been more common historically than in recent years, accounting for almost half of daily IBOC lending during 2008, before falling to around 10 per cent recently (Figure 8). Over the entire sample, 72 per cent of individual rollovers (i.e. those identified by the Furfine-type algorithm) and credit-facility rollovers had been rolled for less than five trading days.
Notes: Share of algorithm-identified lending; excluding weekends and public holidays
As noted earlier, market liaison indicated that risk limits may prevent loans from being rolled over for an extended period. Our results suggest that while this may be a good characterisation of current practice, this was not always the case, with some credit-facility-type loans being rolled over for more than two months before any interest was paid.
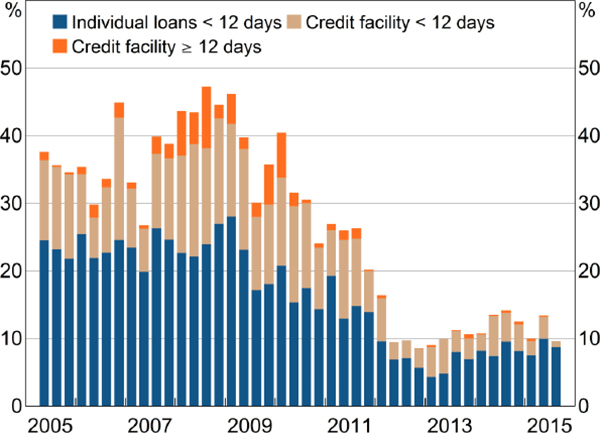
Looking at the values of rollovers and non-rolled loans, the halving of market activity since the beginning of 2009 (shown in Figures 3 and 4) mostly involved a fall in the value of rollovers (Figure 9). The average value of IBOC lending during 2015 was 48 per cent smaller than at the beginning of 2009. This fall comprised an 87 per cent fall in the average value of rollovers and a 13 per cent fall in the average value of non-rolled loans.
In Section 5.3, we discuss some reasons why rollovers and non-rolled loans may not be perfect substitutes. But the cause of the fall in rollovers is unknown, and a detailed analysis is left for future research.
5.2 Timing of IBOC Transactions
RITS is open for settlement from 7.30 until 22.00, but the trading day is split into several ‘sessions’, with different rules governing each session (RBA 2015a). For the purposes of our research, it is sufficient to focus on just three of the sessions (Day, Close and Evening).
The ‘Day’ session finishes at 16.30, at which point new SWIFT customer payments are no longer accepted (customer payments already entered into RITS may be settled in a later session). The ‘Close’ session, operating from 16.30 until 17.15, then allows banks to borrow/lend ESA balances before some banks are able to exit the market.
The ‘Evening’ session opens at 17.20. All ‘evening agreed’ banks must remain available to settle RITS transactions during this session. All SWIFT payments (not just customer payments) involving a ‘non-evening agreed’ bank, and all non-bank Austraclear payments (that are settled via banks' ESAs), must settle before the end of the Close session. As a result, non-evening agreed banks have the option, but are not required, to operate during the Evening session (via cash transfers or Austraclear, not SWIFT). This means that any uncertainty surrounding non-evening agreed banks' end-of-day ESA balances is likely to dissipate earlier in the trading day than it does for evening agreed banks.
During Australian Eastern Standard Time (winter), all SWIFT settlements finish by 18.30; SWIFT settlements can occur until 20.30 during Australian Eastern Daylight Time (summer).[29] As a result, the intraday distribution of RITS transactions (including IBOC loans) differs between summer and winter months.
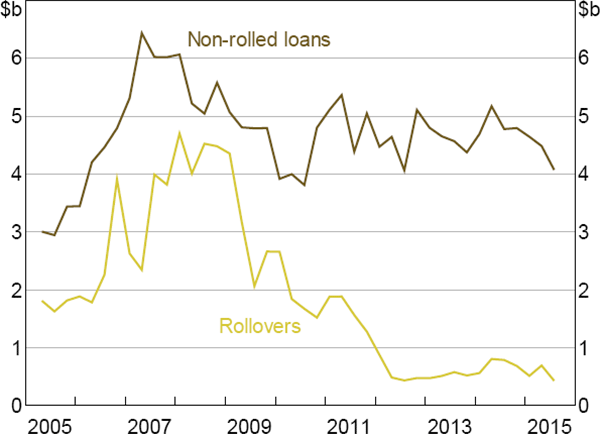
The algorithm output revealed the following features about the timing of non-rolled loans (these include the first days of loans that are subsequently rolled over; Figure 10):
- There is very little non-rolled lending until late in the day, when banks are more certain of their end-of-day ESA balances.
- Non-evening agreed banks are a party to a higher proportion of Day session loans (50 per cent) relative to the Close and Evening sessions (32 and 16 per cent, respectively). This is expected because certainty about their end-of-day positions occurs earlier in the day.
- The majority of non-rolled lending settles during the Close session.
Notes:
Time of first-leg transactions, including increase in principal for credit-facility
loans
(a) Loans for which at least one participant is a non-evening agreed bank
In contrast to first-leg transactions, repayment transactions settle throughout the Day session (Figure 11).
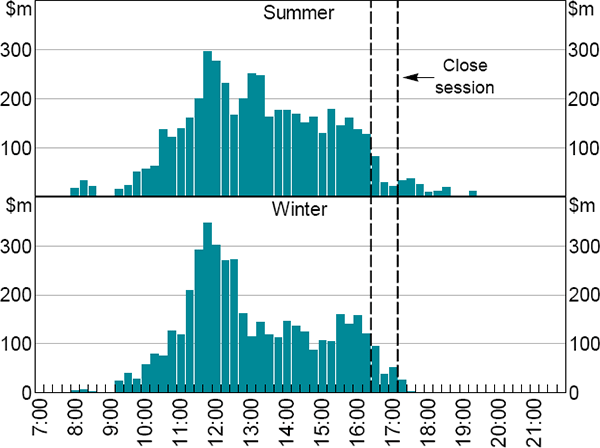
Note: Time of all second-leg transactions, including decrease in principal for credit-facility loans
5.2.1 Changes over time
The share of non-rolled lending that settles during the Close session has increased over time (from 48 per cent in the 2006 winter season to 62 per cent in the 2015 winter season), with a corresponding decrease in both the Day and Evening sessions (Figure 12).[30] This suggests that banks are managing their end-of-day ESA balances during a briefer period than has been the case historically.
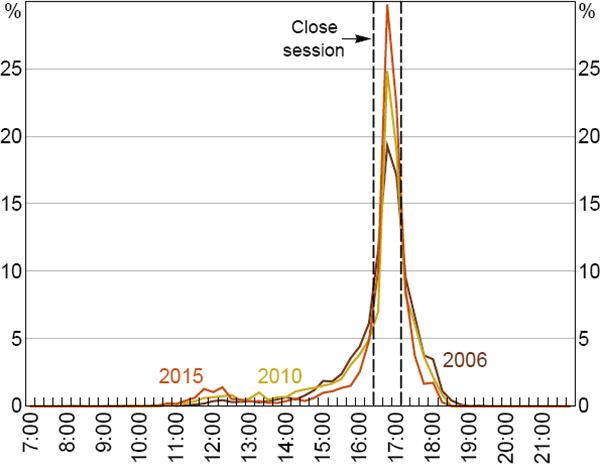
Note: Time of all first-leg transactions
From 25 November 2013, the RBA enhanced RITS to provide for same-day settlement of direct entry obligations in several batches (these transactions were previously settled in a single batch at the beginning of the following business day). With the majority of non-rolled IBOC market activity occurring late in the day, batches that settle early in the day were not expected to affect the IBOC market. Similarly, batches that settle after 16.45 do not affect the IBOC market, because the RBA has implemented alternative arrangements for the settlement of these batches (Fraser and Gatty 2014; RBA 2015c).
That leaves the 16.45 batch as potentially affecting the IBOC market. Although the 16.45 batch settles after one-third of non-rolled IBOC loans had historically already settled, banks have information on the size of this batch before 16.15. As a result, banks' uncertainty about their end-of-day ESA balances, at times when the majority of non-rolled IBOC activity had historically occurred (i.e. the Close and Evening sessions), was not expected to change following the introduction of same-day settlement. So the 16.45 batch was not expected to further delay market activity.
The data is consistent with this expectation. While there was an increase in the proportion of Close session settlements between 2012 and the period immediately following the introduction of same-day settlement (from 38 to 42 per cent; Figure 13), a two-sample Kolmogorov-Smirnov test is unable to reject (at the 10 per cent significance level) the null hypothesis that the 2012 and 2013 distributions are the same. Moreover, this increase is consistent with the trend increase in Close session settlements discussed above. And the corresponding decrease in the share of settlements mainly occurred in the Evening session, which is inconsistent with the 16.45 batch causing a delay in market activity.
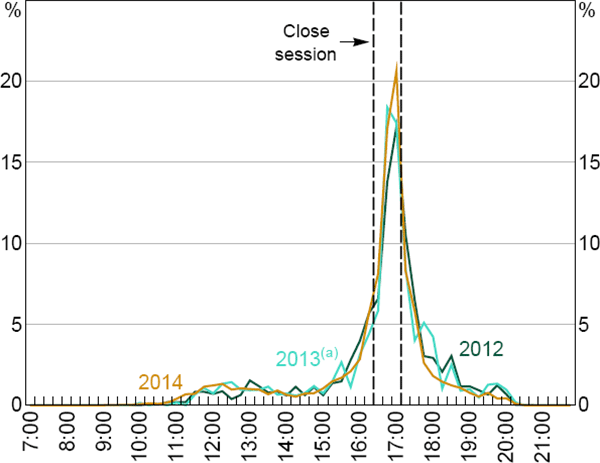
Notes:
Time of all first-leg transactions
(a) 25 November–31 December only
5.3 Timing of Rollovers and Non-rolled Loan Agreements
Knowing the time of day at which rollovers are typically agreed may help to explain why the value of rollovers has declined so dramatically since 2009 while non-rolled loans have remained broadly stable (Figure 9). However, since rollovers do not have a corresponding RITS transaction on each day they are rolled, it is not possible to determine the time of day at which each rollover is agreed. Nevertheless, since the IBOC Survey asked respondents to split their gross lending/borrowing figures into the trading sessions in which the loans were agreed, we can estimate the sessions in which rollovers are typically agreed by comparing the algorithm-identified value of daily rollovers to the survey data over time (using regression techniques).[31]
Knowing agreement times is also important for operational decisions made by the RBA (as was discussed at the beginning of Section 5). And it is possible that non-rolled loans may be agreed in one session and settled in another (the analysis in Section 5.2 is based on settlement time rather than agreement time). Our regression analysis is also able to estimate the typical share of non-rolled loans agreed in one session and settled in another.
If there were no rollovers and the algorithm were 100 per cent accurate, we would be able to determine the exact value, every day, of IBOC loans agreed in one session and settled in another (by comparing the survey data to the algorithm output for each session). The regression analysis is required because random changes in the agreement time of rollovers, and loan-identification errors from the algorithm (i.e. false positives and negatives), confound our ability to identify daily differences in agreement and settlement times.
Moreover, the potential size of these confounding factors is likely to vary with the value of IBOC market activity (e.g. the value of false negatives is limited by the true value of lending), causing conditional heteroskedasticity. And random changes in the agreement time of rollovers would be negatively correlated across sessions (i.e. a higher than expected share of rollovers in one session necessitates a lower than expected share in another session).
For these reasons, we implement our regression analysis using a three-equation (one for each session) seemingly unrelated regression (SUR) model with conditional heteroskedasticity.[32] The model is:
where:
- i = Day (1), Close (2), or Evening (3) sessions
- t = trading day
- diffi,t = difference between the value of loans agreed in session i of day t (from the IBOC Survey) and the algorithm-identified value of non-rolled loans[33] settled in session i of day t
- rollt = value of rollovers (identified by the algorithm) in day t
- nrt = value of non-rolled loans (identified by the algorithm) in day t
- ui,t = residual component of diffi,t; modelled as a first-order autoregression
- εi,t = unexplained component of ui,t (assumed to be a random draw from a multivariate normal distribution)
- ωi,t = conditionally-heteroskedastic variance of εi,t
- ci,j = contemporaneous correlation between εi,t and εj,t
-
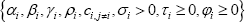 are the parameters to be estimated for each session
i.
are the parameters to be estimated for each session
i.
The remainder of this section provides interpretations for the parameters of interest, explains some potential biases that may hamper estimation, details the estimation results, and discusses the implications of these results. A formal derivation of the model's functional form and the asymptotic properties of the parameter estimators are given in Appendix D.
5.3.1 The parameters of interest and potential biases
Starting from Equation (1), suppose, for the moment, that the following conditions hold:
- no loan-identification errors;
- the shares of rollovers agreed in each session are constant over time; and
- the shares of non-rolled loans agreed in one session and settled in another are constant over time.
Then αi + ui,t = 0 for all i and t. This is because, in this scenario, diffi,t has just three components: rollovers agreed in session i, plus non-rolled loans agreed in session i but settled in a later session, minus the value of non-rolled loans settled in session i that were agreed in a previous session. And with these three components being a constant share of the daily aggregates (in this scenario), diffi,t = βirollt + γinrt for all i and t.
Moving away from this stylised scenario, diffi,t = βirollt + γinrt does not hold due to loan-identification errors, changes in the per session shares of daily rollovers, and changes in the per session shares of daily non-rolled loans that are agreed and settled in different sessions. All of these components are captured in αi + ui,t; with ρiui,t − 1 capturing the persistence in these components, αi capturing the mean, and εi,t being the unexplained portion of these components.[34]
Therefore, given what this section seeks to determine, the parameters of interest and their interpretations are:
- βi – the typical share of daily rollovers agreed in session i; and
- γi – the typical share of daily non-rolled loans agreed in session i and settled in a later session, minus the typical share settled in session i that was agreed in an earlier session.
Because the shares of daily rollovers agreed in each session must sum to 100 per cent, random changes in these shares induce negative correlations between the session-specific shocks (εi,t). Random changes in the share of daily non-rolled loans agreed in session i and settled later minus the share settled in session i that was agreed earlier' (henceforth, ‘net share’) also induce negative correlations. For example, a reduction in the share agreed in Session 1 and settled in Session 2 would reduce the Session 1 net share but increase the Session 2 net share. This is why a SUR framework is used (i.e. why non-zero ci,j parameters are allowed).
As long as these random changes in shares are independent of the daily values of rollovers and non-rolled loans, these random changes will not cause our parameter estimators to be inconsistent (see Appendix D). However, the impact of these random changes on the variances of the session-specific shocks (ωi,t) will depend on the daily values of rollovers and non-rolled loans, which is why we incorporate conditional heteroskedasticity into our model (see Appendix D).
Unfortunately, our parameter estimators will be inconsistent if the loan-identification errors are correlated with the daily values of rollovers or non-rolled loans (see Appendix D). Such correlation is a reasonable assumption given that the value of false negatives on any day is bounded by the true value of lending.[35] However, given the accuracy of our algorithm, we do not expect any inconsistencies to be large.
To potentially help attenuate any estimator inconsistency, we impose theory-based restrictions on the βi parameter estimators. First, since rollovers must be agreed at some point during the day, the sum of the shares agreed in each session must equal 1 (i.e. ∑iβi = 1). Second, rollovers cannot reduce the difference between the IBOC Survey and algorithm output (i.e. βi ≥ 0 ∀ i).[36]
5.3.2 Estimation results
Table 2 shows the βi parameter estimates produced by maximum likelihood estimation of the model (with the aforementioned restrictions) for four datasets: the lending/borrowing of the major banks, and the lending/borrowing of the 18 other banks that were included in the IBOC Survey from early in the sample.[37] The results suggest that rollovers are typically agreed in the Day session. This is not surprising given that the majority of repayments occur during the Day session (Figure 11), and rollovers would need to be agreed before repayment was due.
While almost all of the rollovers to which the major banks are a party are typically agreed in the Day session, more than 10 per cent of the other banks' rollovers are typically agreed in the Close session. The hypothesis that all rollovers are agreed in the Day session is statistically rejected at the 5 per cent level for all four regressions in Table 2.
| Day | Close | Evening | |
|---|---|---|---|
| Major banks' lending | 98 (102) | 0 (−4) | 2 (5) |
| Major banks' borrowing | 96 (91) | 3 (2) | 1 (1) |
| Other banks' lending | 83 (81) | 16 (16) | 0 (0) |
| Other banks' borrowing | 86 (78) | 11 (10) | 4 (3) |
For the major banks, the theoretical restrictions are statistically rejected by the data (at the 1 per cent level); the unrestricted estimates are given in parentheses in Table 2. Given that the restrictions must hold with the true parameter values, the fact that they are statistically rejected suggests our concerns about estimator inconsistency are well-founded. That said, the differences between the restricted and unrestricted estimates would not change our qualitative conclusions, so the inconsistency is not qualitatively important (as expected). For the other banks, likelihood ratio tests of the theoretical restrictions produce p-values of 0.90 for lending and 0.09 for borrowing.
With the γi parameters representing the typical ‘net shares’, the γi parameters would sum to zero (in the limit) in the absence of estimator inconsistencies. As shown in Table 3, the sum is less than zero for three of the four regressions, suggesting that, for at least some sessions, loan-identification errors are negatively correlated with the value of identified non-rolled loans.
| γi parameters Per cent |
Correlations (ci,j) |
|||||
|---|---|---|---|---|---|---|
| Day | Close | Evening | Sum | Day/Close | Close/Evening | |
| Major banks' lending | 2 | 18 | −25 | −5 | −0.15 | −0.77 |
| Major banks' borrowing | 6 | 15 | −24 | −3 | −0.32 | −0.79 |
| Other banks' lending | 11 | 0 | −17 | −6 | −0.34 | −0.61 |
| Other banks' borrowing | 20 | −7 | −12 | 1 | −0.36 | −0.28 |
Assuming the correlations between loan-identification errors and identified non-rolled loans have the same sign in every session, the estimated γi parameters can still be used to provide a range for the estimated proportion of non-rolled loans typically agreed in the Close session and settled in the Evening session.[38] For the major banks, this range is 20–25 per cent for their lending and 21–24 per cent for their borrowing. For the other banks, the range is 11–17 per cent for their lending and 12–13 per cent for their borrowing.[39]
Since 45 per cent of the major banks' non-rolled lending, and 37 per cent of their non-rolled borrowing, settles in the Evening session (on average over the sample), these results suggest that the majority of this lending/borrowing was actually agreed in the Close session. This means that 75–87 per cent of the major banks' non-rolled lending/borrowing is estimated to have been agreed before the end of the Close session. This proportion is 91–99 per cent for the other banks.
As expected, the session specific shocks (εi,t) are negatively correlated between consecutive sessions (Table 3), while the correlations between non-consecutive sessions are close to zero (with absolute values less than 0.03).[40] The conditional heteroskedasticity (i.e. the τi and φi parameters in Equation (4)) is estimated to be statistically significant (at the 1 per cent level) in all four regressions.
5.3.3 Implications of these results
Combining the results presented above with those from Section 5.2 suggests that rollovers are typically agreed earlier in the day than non-rolled loans (when banks may be less certain of their late-day funding needs). However, rollovers still appear to be used by banks to manage their end-of-day ESA balances. If a bank lends via a rollover, the probability of that bank also lending via a non-rolled loan on that day is 75 per cent, while the probability of borrowing via a non-rolled loan is just 42 per cent.[41] The conditional probabilities when borrowing via rollover are similar, with the probability of non-rolled borrowing at 76 per cent, and non-rolled lending at 40 per cent.[42]
With banks appearing to use both rollovers and non-rolled loans to manage their end-of-day ESA balances, the fact that the majority of the fall in rollovers (between 2009 and 2015) occurred while non-rolled loans remained broadly steady suggests that the cause of the fall in rollovers is unlikely to be a fall in generic late-day funding needs. For example, Hing, Kelly and Olivan (forthcoming) suggest that the fall in rollovers may be due to a fall in precautionary demand for ESA balances, with this precautionary demand satisfied via rollovers.
Moreover, there may be other reasons (beyond time of day) why rollovers and non-rolled loans may not be perfect substitutes (such as the increasing credit risk with each day it is rolled over).[43] So it may be a feature of rollovers that has led to the fall. The first port of call will be to determine whether the fall in rollovers corresponds with increased activity in other markets (such as the term or secured lending markets).
5.4 Number and Average Value of Loans
Over the entire sample, quarterly changes in the average number of loans per day and changes in the average value of these loans have been roughly equal contributors to the changes in the value of IBOC loans (Figure 14).[44]
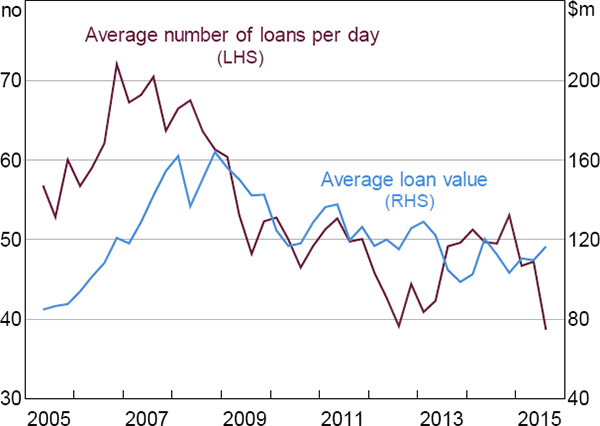
The fall in the average number of loans per day is mainly composed of a fall in the average number of rollovers, with the average daily number of non-rolled loans at the end of the sample (33) being little changed from the beginning (36). Until 2009, the average sizes of rollovers and non-rolled loans were essentially the same (the average absolute difference during this period was just 8 per cent of the level). As the number of rollovers fell, the remaining rollovers were typically smaller than the non-rolled loans ($78 million versus $123 million, respectively).
5.5 Simple Interest for Rollovers
Of the 96,052 first-leg transactions the Furfine-type algorithm identifies as being part of an IBOC loan, only 9 were repaid with compound interest (with these potentially being false positives). Instead, the interest owed on rollovers is almost always calculated using simple interest. For example, a loan rolled over from Monday to Thursday is repaid as principal plus 3 times daily simple interest. This means that when calculating repayments on rollovers, lenders are not accounting for any interest that was owed to them throughout the rollover period; in other words, borrowing banks that roll over are essentially receiving small interest-free loans.[45] With several banks borrowing more than double the amount they lent (between 2005 and 2015), this lack of compounding has benefited some banks more than others.
Footnotes
In Section 5, ‘rollovers’ refer to loans for which some of the first-leg transactions occurred on a previous day. This differs from the definition in Section 4, in which the first day of a loan that was subsequently rolled over was also excluded. This is because Section 4 was focused on highlighting the novel features of our algorithm, as opposed to highlighting the features of the market. [27]
For example, a delay of expected payments could cause some banks to delay their IBOC market activity, thereby reducing liquidity during some parts of the day and potentially leading other banks to lend/borrow away from the target cash rate. [28]
The different summer and winter finishing times result from the requirement that simultaneous settlement of both legs of some foreign exchange transactions must be possible during the European morning (RBA 2015a). [29]
A similar trend is exhibited between the summer seasons of 2006 and 2015.
Two-sample Kolmogorov-Smirnov tests (that compare two sample probability distributions,
e.g. comparing 2006 to
2010) reject, at the 5 per cent significance level, the null hypotheses that any two of
these distributions are the same.
[30]
In essence, the survey contains information about agreement times but no information about the split between rollovers and non-rolled loans. Conversely, the algorithm output provides this split, but provides no information about agreement times. Regression techniques allow us to determine the typical agreement times of rollovers by comparing these two information sources over time. [31]
The null hypothesis of non-stationarity was statistically rejected for all variables at the 1 per cent level of significance (using Phillips-Perron unit root tests). [32]
For this model, ‘non-rolled loans’ include increases in the principal of credit-facility loans. This is because our dataset includes the settlement times of these transactions. These increases in principal account for less than 3 per cent of all first-leg transactions. [33]
These autoregressive coefficients (ρ1, ρ2, ρ3) are estimated to be jointly statistically significant at the 1 per cent level. Including autoregressive terms up to the third order did not change our qualitative conclusions. [34]
However, the expected direction of the inconsistency is not clear. While false negatives
are expected to cause loan-identification errors to be positively correlated with the
true value of lending, they can still be negatively correlated with the identified
value of lending.
Conversely, since false positives arise from non-loan payments randomly satisfying the
algorithm criteria, and with the value of these non-loan payments far exceeding the
value of IBOC loans, we do not expect false positives to be correlated with either the
true or identified value of lending.
[35]
While these restrictions prevent any aggregate inconsistency, the session-specific parameter estimators may still be inconsistent, with the restrictions potentially redistributing the inconsistencies among these estimators. [36]
The results reported here are qualitatively similar to the estimates derived from feasible generalised least squares estimation. [37]
If the correlations between these errors and non-rolled loans have the same sign in every session then, in the limit, the γi estimators are either all lower or all higher than they would be without the errors (see Appendix D). [38]
This is a range for the point estimate, not a statistical confidence interval. Using the 95 per cent confidence intervals for each γi parameter extends these ranges by a maximum of 6 percentage points either side. [39]
The hypothesis that the correlations for each regression are all zero is statistically rejected at the 1 per cent level for all four regressions. [40]
These are weighted-average probabilities based on the 22 banks included in the IBOC Survey from early in the sample, and weighted by each bank's frequency of rollovers between 2005 and 2015. [41]
On any given day, the unconditional probability of a randomly drawn bank being a lender is the same as the unconditional probability of it being a borrower (since for every lender there must be a borrower); these probabilities would be greater than 50 per cent if some banks intermediate the funding of other banks. If rollovers were conducted independently of a bank's late-day funding needs, borrowing via a rollover would increase the probability of this bank lending via non-rolled loans later in the day (because the bank would, in expectation, need to offset the impact of the rollover on their end-of-day ESA balance). However, we find that the probability of non-rolled borrowing following rolled-over borrowing is significantly higher than the probability of non-rolled lending (at the 1 per cent significance level); the difference in the probabilities following rolled-over lending is also statistically significant. This suggests that, while rollovers are used to satisfy expected late-day funding needs, banks are typically either unwilling or unable to fully satisfy their expected funding needs via rollovers (with symmetric late-day uncertainty, fully satisfying expected late-day funding needs via rollovers would leave a bank's conditional non-rolled borrowing and lending probabilities identical). [42]
With each day it is rolled over, the lending bank cannot be certain that the borrowing bank would have been able to repay the loan if it were not rolled. [43]
A variance decomposition of the log-differences of IBOC loans attributes 50.2 per cent to log-differences of the average value of loans and 49.5 per cent to log-differences of the average number of loans (with a covariance share of 0.3 per cent). [44]
For example, with $4.7 billion of daily rollovers (the average in the first quarter of 2008), rolled for 8 trading days (the weighted average rollover length during this quarter), and with a target cash rate of 7 per cent (the average during this quarter), the lending banks would lose around $320,000 per year by allowing interest to be calculated without compounding. [45]