RDP 2016-11: Identifying Interbank Loans from Payments Data 3. The Algorithm
December 2016
- Download the Paper 3.19MB
Our algorithm is composed of two parts. The first part, which we call the Furfine-type algorithm, is based on the work of Furfine (1999) and other papers that have followed a similar procedure (see Appendix A), but is extended to identify rollovers; such an extension is a novel contribution to the literature. The second part, which we call the credit-facility algorithm, identifies IBOC loans with features that cannot be picked up by Furfine-type algorithms. Our credit-facility algorithm is an innovation for the loan-identification literature and, as is shown in Section 4, is necessary when applying the algorithm to the Australian market.
3.1 The Furfine-type Algorithm
Using transaction-level payments data, existing Furfine-type algorithms typically identify a pair of transactions that could feasibly be considered the ‘first’ (initial payment) and ‘second’ (repayment) legs of an IBOC loan. This is done by matching transactions for each pair of counterparties over two consecutive trading days, where the second transaction goes in the reverse direction and is equal to repayment of the first transaction plus a feasible amount of interest.
Feasibility is determined by proximity of the implied interest rate (i.e. the rate implied by comparing the values of the first and second legs) to some external information about reasonable interest rates in the IBOC market. This could be, for example, information on the range of interest rates observed during the day, the average daily interest rate, or the target policy rate.
As a simple example, suppose there is a $1,000,000 payment going from Bank A to Bank B on Tuesday, and a $1,000,150 payment going from Bank B to Bank A on Wednesday. The annualised implied simple interest rate is 5.475 per cent. If the average IBOC interest rate on Tuesday was 5.47 per cent, an implied interest rate of 5.475 per cent may be considered sufficiently close to the average IBOC rate for these two transactions to be identified as an IBOC loan.
The first part of our algorithm uses this basic structure but is more flexible. In addition to looking for next-day repayments of principal and interest, our algorithm searches for repayment transactions over multiple days (to allow for rollovers), and allows for repayment structures that previous research had indicated would confound typical Furfine-type algorithms (such as principal being repaid in a separate transaction to interest).[6] Allowing for rollovers requires increased flexibility along several dimensions:
- cumulative interest may be paid on the same day as the principal repayment (either in the same transaction or separately) or interest may be paid daily;
- interest payments could be calculated using either simple or compound interest (if interest is not paid daily); and
- the set of feasible implied interest rates may change on a daily basis.
Market liaison indicated that risk limits may prevent IBOC loans from being rolled over for an extended period, so we limit our search for repayment transactions to 15 calendar days.[7] Market liaison also indicated that IBOC loans are typically conducted in multiples of $1 million. So all transactions that are not a multiple of $1 million are excluded from the sample of potential first-leg transactions (but remain as potential repayment transactions).
As with previous applications of Furfine-type algorithms, our algorithm requires a mechanism to ensure that each transaction is associated with at most one loan, and that each loan is associated with the correct number of transactions. A detailed description of this mechanism, and the rest of the Furfine-type algorithm, is provided in Appendix B.
3.2 Credit-facility Lending
Credit-facility lending occurs when a bank borrows (overnight) from the same counterparty over several consecutive days, but where:
- the value of the overnight loans may change on a daily basis;
- there are daily transactions that correspond to the change in the principal of the loan (there may be more than one transaction per day);
- the cumulative interest is paid in one lump sum at some point in the future (not necessarily in the same transaction as any principal repayment); and
- part (or all) of the principal outstanding when cumulative interest is paid may be rolled over into a new loan.
A hypothetical example of IBOC loans with these features is shown in Table 1. Two notable features in this example are that the additional lending on Tuesday occurs in two separate transactions, and that there is only partial repayment of the outstanding principal on Thursday, with the remaining principal rolled over into another IBOC loan.
| Day | Payer | Receiver | Payment | Loan size | Interest outstanding at end of day |
|---|---|---|---|---|---|
| Monday | A | B | $1m | $1m | $150 |
| Tuesday | A | B | $3m | $6m | $1,050 |
| Tuesday | A | B | $2m | ||
| Wednesday | B | A | $3m | $3m | $1,500 |
| Thursday | B | A | $2m + $1,500 | $1m | $150 |
| Friday | B | A | $1m + $150 | $0 | $0 |
With interest paid in a lump sum, and the loan principal changing during the rollover period, there is no single first-leg transaction that represents the principal of the loan. Therefore, an implied interest rate cannot be calculated in the same way as a Furfine-type algorithm, requiring our credit-facility algorithm to be fundamentally different from Furfine-type algorithms. A rudimentary description of the credit-facility algorithm is given in Section 3.3; see Appendix B for a detailed description.[8]
3.3 The Credit-facility Algorithm
The credit-facility algorithm starts by treating all transactions as potential first legs of IBOC loans, and then begins a process of elimination.[9] First, all transactions identified by the Furfine-type algorithm as already being part of an IBOC loan are removed from the sample. Then, as in the Furfine-type algorithm, all transactions that are not a multiple of $1 million are excluded from the sample of potential first-leg transactions (but remain as potential repayment transactions).
From this point, the credit-facility algorithm aggregates the potential first-leg transactions between each pair of banks, on each day. These daily flows are then added to (or subtracted from) each bank's potential bilateral principal outstanding from the previous day. At this point in the algorithm, transactions are only ‘potential’ IBOC loan transactions; they will not be confirmed as IBOC transactions until later in the algorithm.
We assume that, in any pairing, only one bank can have loans outstanding to the other. Therefore, whether the daily flows are treated as increasing or decreasing principal depends on the direction of the net flows and which bank had positive principal outstanding at the end of the previous day.
For example, suppose Bank A had a $100 million IBOC loan from Bank B on Day 1. A net flow of $30 million from A to B on Day 2 would be treated as Bank A receiving a $70 million IBOC loan from Bank B on Day 2 (i.e. Bank A is assumed to have repaid some principal, rather than granting Bank B a $30 million loan), whereas a net flow of $30 million from B to A would be treated as Bank A receiving a $130 million IBOC loan from Bank B on Day 2.
For each day that a potential IBOC loan exists between a pair of banks but interest is not paid the following day, the potential interest outstanding between this pair of banks increases. Based on an ex ante determined feasible set of daily interest rates, the algorithm computes a minimum and maximum for potential interest outstanding.
On each day, the algorithm checks all transactions (from borrower to lender) between each pair of banks to determine if any could feasibly include an interest payment (with feasibility determined by the minimum and maximum outstanding). If a transaction is found that equals the full repayment of principal plus interest, then this transaction and all first-leg transactions that contributed to the outstanding principal are verified as IBOC loan transactions.
A transaction may also be found that amounts to either an interest-only payment or an interest plus partial principal repayment. For either of these to be verified as IBOC transactions, the remaining principal must form part of a new IBOC loan. The algorithm ensures that this is the case.
Without any further refining of potential IBOC transactions, any rounded transaction (i.e. any transaction that is a multiple of $1 million) that is not part of an IBOC loan would bias the potential interest outstanding on all future days, potentially preventing future IBOC loans from being identified. To prevent this, the algorithm limits the number of days interest can remain outstanding before the relevant first-leg transactions are established as non-IBOC transactions and excluded from the sample (akin to the rollover limit in the Furfine-type algorithm).[10]
When the limit for interest outstanding has been reached, the algorithm removes the offending first-leg transactions from the sample (i.e. the transactions on the first day that contributed to the interest outstanding). It then recomputes the potential principal and interest outstanding for both banks and every intervening day (i.e. every day between the day of the sample adjustment and the current day). It also re-checks whether any transactions on these intervening days could feasibly include an interest payment (in the same way as discussed above).
When the algorithm finishes, the only rounded transactions remaining in the sample are those that have been verified as first legs of IBOC loans. If they were not verified, the algorithm would have removed them from the sample when the relevant interest outstanding limit had been reached.[11]
Even though all IBOC loan transactions need to be ‘verified’, the algorithm can falsely identify transactions as IBOC loan-related if they randomly satisfy all of the algorithm's verification criteria (this is known as a Type I error or false positive); this is also a problem for Furfine-type algorithms. The incidence of false positives can be reduced by imposing stricter criteria. For example, the feasible range of interest rates could be narrowed or the interest outstanding limit could be shortened. As will be shown in Section 3.4, the probability of false positives will be very low with our calibration of the algorithm.
The bigger issue for the credit-facility algorithm is erroneous exclusion from the sample (i.e. a Type II error or false negative). This is because, on a given day and for each pair of banks, the algorithm either includes all rounded transactions or excludes them all; it does not independently validate each transaction.[12] As a result, rounded non-IBOC transactions can prevent loans from being identified.
For example, suppose rounded transactions between a pair of banks on a given day include both IBOC loan transactions and other transactions. Until the interest outstanding limit is reached, interest outstanding calculations will be erroneously based on all of these transactions. This means that any true interest payment may fall outside the calculated feasible range of interest outstanding, preventing all transactions associated with these true IBOC loans (which may be rolled over for several days) from being validated.[13]
As the Furfine-type algorithm is not subject to the same false negative problem as the credit-facility algorithm – because each interest payment is matched with a single first-leg transaction – the Furfine-type algorithm is run on transactions entered into RITS via either cash transfers or Austraclear (over 900,000 rounded transactions between 2005 and 2015).[14] Both market liaison and the results from the Furfine-type algorithm suggested that the majority of IBOC transactions were entered via cash transfers.[15] Moreover, the number of rounded transactions entered via Austraclear was far larger than the number entered via cash transfers, increasing the likelihood of false negatives. Therefore, the credit-facility algorithm is only run on transactions entered through cash transfers (less than 40,000 rounded transactions between 2005 and 2015, after excluding those identified by the Furfine-type algorithm as IBOC loans).[16]
While using a subset that contains fewer rounded transactions reduces the feasible number of false negatives from within that subset, all IBOC transactions outside of this subset will be false negatives by construction. However, based on the accuracy of the algorithm's output, the incidence of false negatives appears to be low (see Section 4).
3.4 Feasible Interest Rates in Australia
To reduce the incidence of false negatives, past work using these Furfine-type algorithms has allowed the implied interest rate on a matched pair of transactions to differ from the target policy rate and to still be classified as an IBOC loan. For example, Furfine's original work allowed for an implied interest rate 50 basis points above the highest rate that was reported on each day, and 50 basis points below the lowest rate (Furfine 1999).
While allowing for a range of interest rates may be necessary in other markets, a well-known feature of the Australian market is that IBOC lending typically occurs with an interest rate equal to the target cash rate. The average daily interest rate on these loans deviated from the target cash rate just 14 times between 2005 and 2010 (each deviation was less than 4 basis points); there have been no deviations since 2010 (Figure 1).
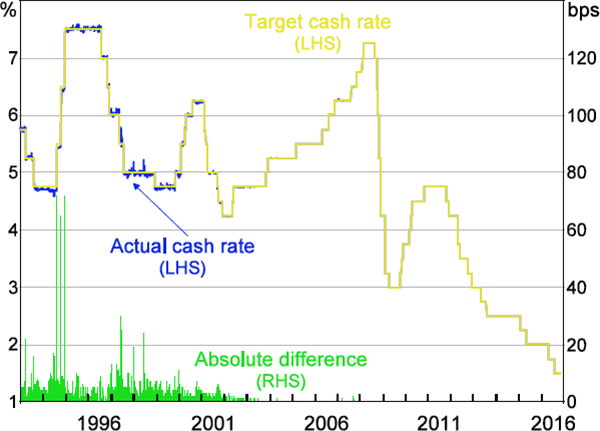
Note: Rounded to nearest basis point
Sources: Authors' calculations; RBA
As a result, capturing IBOC loans in Australia requires a much smaller interest rate range than international studies. This reduces the incidence of false positives, thereby increasing the accuracy of the algorithm (false positives have been a problem for previous applications of Furfine-type algorithms; see Appendix A).
Using 2015 as an example, suppose we restrict the dataset to Furfine-type algorithm matches that imply an interest rate within 100 basis points of the target cash rate, and where the repayment of principal and interest is combined within a single transaction (Figure 2).[17] Then 84.4 per cent of these observations have an implied interest rate equal to the target cash rate. Expanding the range to ±1 basis point around the target captures 84.7 per cent, while a ±5 basis point range captures 85.2 per cent. So expanding the range has little impact on the number of potential loans captured by the algorithm, implying that the incidence of combined-repayment false negatives is low even with an interest rate range of 0 basis points around the target cash rate.
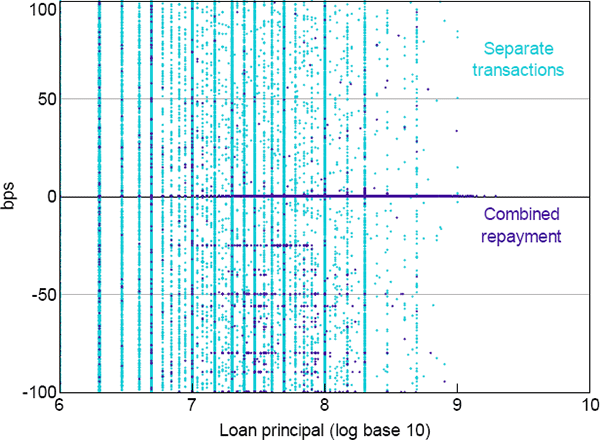
The story is very different when the sample is changed to Furfine-type algorithm matches where the principal is repaid in a separate transaction to interest (Figure 2). There are roughly four times the number of observations relative to the combined-repayment sample, and they are more widely dispersed. This is because there are a large number of small-value payments in our dataset, so there is a high probability of randomly matching two equal-sized payments (i.e. payment and repayment of principal) with a third transaction that would imply an interest rate within 100 basis points of the target cash rate. So, while the large number of small-value payments increases the probability of false positives (relative to the combined-repayment sample), the wide dispersion of the separate transaction observations means the incidence of false negatives could be high with small interest rate ranges (relative to the combined-repayment sample).
The numbers of separate transaction observations captured with implied interest rate ranges of ±1 and ±5 basis points are less than would be expected if none of the separate transaction observations were actually loans but were instead randomly distributed (so we can't statistically rule out the possibility that they are all false positives).[18] However, we can't simply exclude all separate transaction observations, because the number of observations at the target cash rate is significantly above what would be expected if they were false positives.[19]
To summarise, when expanding the allowable interest rate range beyond 0 basis points around the target cash rate, we find small numbers of extra combined-repayment observations, with some of these potentially being false positives. The numbers of extra separate transaction observations at ranges beyond 0 basis points are much larger, but no more than what would be expected if they were all false positives. So we are confident that we are able to minimise the frequency of false positives (by setting an interest rate range of 0 basis points), while still capturing the majority of the IBOC market (i.e. while retaining a low frequency of false negatives).[20]
As noted earlier, while previous international research has discussed the possibility of rollovers, existing algorithms do not attempt to identify them. This is probably because, with sufficiently wide interest rate ranges, it may not be possible to distinguish rolled-over IBOC loans from term lending.[21] Since any term lending captured by the 0 basis point calibration of our algorithm would require these loans to have a term premium of zero and a perfect forecast of future overnight rates, and due to the accuracy of our algorithm's output (see Section 4), we are confident that we are capturing rolled-over IBOC loans rather than term lending.
Given the prevalence of rollovers in the Australian market (see Sections 4 and 5), the ability to identify rollovers (both Furfine-type and credit-facility) is an important innovation to this literature. To the extent that rollovers occur in other countries, the novel features of our algorithm may also improve the identification of overnight interbank loans in these countries. This is particularly the case for countries where low daily interest rate volatility may permit a small interest rate range (such as Canada, see Hendry and Kamhi (2007)).
Footnotes
In this paper, the term ‘repayment transaction’ refers to any transaction
that is part of a loan repayment (e.g. an interest payment is classified as a repayment
transaction).
To our knowledge, Demiralp et al (2004) is the only other paper with
an algorithm that allows for principal to be repaid in a separate transaction to
interest. Other papers note that typical Furfine-type algorithms will not pick up loans
with this structure (e.g. Armantier and Copeland 2015).
[6]
Increasing the maximum number of days for which a loan can be rolled (rollover limit) to one month had little impact on the results (increasing the number of identified first-leg transactions by just 0.5 per cent). [7]
The credit-facility algorithm will also capture situations in which multiple non-rolled loans are repaid with a single transaction the following day. Multiple loans with combined repayments are not captured by Furfine-type algorithms. [8]
For simplicity when describing the credit-facility algorithm (i.e. in this section), any transaction that changes the size of a credit-facility loan and does not include an interest payment is defined as a ‘first-leg’ transaction (even if the transaction reduces the size of the loan). Second-leg transactions are defined as transactions that include interest payments. [9]
As will be shown in Section 5.1, to fully capture the Australian market the credit-facility limit must be set higher than the 15-day limit used in the Furfine-type algorithm. [10]
The sample of ‘verifiable’ transactions is shorter than the full sample. This is because the algorithm will not be able to eliminate non-IBOC transactions that occur closer to the end of the sample than the interest outstanding limit. Similarly, IBOC transactions close to the beginning of the sample may be erroneously eliminated because the interest payment covered first-leg transactions that occurred before the beginning of the sample. As a result, all analyses in this paper are conducted on a truncated sample of verifiable transactions (see Appendix B for details). [11]
Independent validation of each transaction would require the algorithm to solve a large number of subset-sum problems. With a potentially large number of transactions and large precision (i.e. the set of possible sums), independent validation would increase the algorithm's run time, with little gain given the accuracy of the existing algorithm (see Section 4). [12]
This problem is compounded by the trade-off between Type I and Type II errors. For example, narrowing the feasible interest range to reduce the probability of Type I errors increases the likelihood that a true interest payment will fall outside the calculated range of feasible interest outstanding. [13]
Including non-rounded transactions (as potential repayment transactions), there were 7.4 million transactions entered into RITS via cash transfers and Austraclear between 2005 and early 2016. [14]
As a share of the total number and value of transactions identified by the Furfine-type algorithm (both first and second legs), those entered via Austraclear account for 30 per cent and 17 per cent, respectively. [15]
Around one-quarter of these 40,000 rounded transactions were identified as being part of an IBOC loan. [16]
The observations in Figure 2 are vertically grouped because the algorithm only allows principal values in multiples of $1 million. The horizontal axis uses a base 10 logarithm scale, so the principal values of the loans at 6 are $1 million, 7 are $10 million, etc. [17]
That is, if the implied interest rates of the separate transaction observations within ±100 basis points of the target cash rate followed a uniform distribution. [18]
After rounding observations' implied interest rates to the nearest 0.01 basis point, there are 27 separate transaction observations at the target cash rate. This compares with an expectation of 4, and a Monte Carlo simulation 95 per cent confidence interval upper bound of 8. [19]
See Appendix C for further discussion of how expanding the interest rate range impacts the accuracy of the algorithm output. [20]
Papers that use Furfine-type algorithms to identify unsecured term loans include Heijmans, Heuver and Walraven (2010), Kuo et al (2014) and Arciero et al (2016). However, if the interest rate range covers rates that are feasible for both rollovers and term loans, these algorithms would be unable to distinguish term lending from any rollovers for which the interest is paid on the same day as the principal repayment. [21]