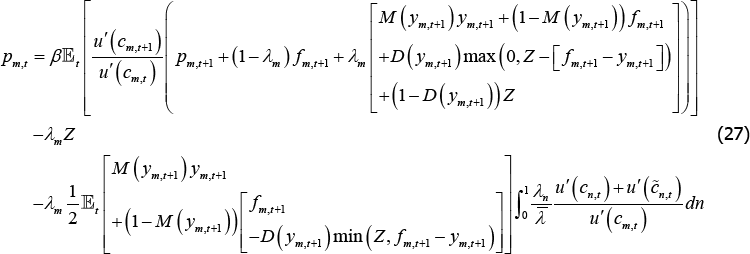RDP 2016-07: The Efficiency of Central Clearing: A Segmented Markets Approach 4. Results
October 2016
- Download the Paper 2.00MB
4.1 The Value of OTC Derivatives
OTC derivatives are valuable because they enable traders to hedge their idiosyncratic endowment risk and reduce the variance of their consumption. Because traders are risk averse, these hedges are valuable and provide a motivation for trade. The left-hand panel of Figure 4 highlights the result that the benefits of OTC derivatives are highest when they provide a more effective hedge – that is, when the correlation between the contract payment (ym,t) and the idiosyncratic endowment stream (Am,t) is more negative (approaches minus one). As the correlation between Am,t and ym,t becomes weaker (less negative), traders' hedges are less effective at reducing their consumption variance. In the extreme, with zero correlation, OTC derivatives have no social welfare value because traders cannot use them to reduce the variance of their consumption.
The right-hand panel of Figure 4 highlights the result that, as the probability of default rises (and so counterparty credit risk increases), the benefit of OTC derivatives falls. Default has two effects. First, default means that traders do not get paid when the ym,t movement is most favourable, because their counterparty defaults. On the other hand, because default is symmetric, traders do not have to pay when they receive a very adverse ym,t. The former effect outweighs the latter because the contract pay-off is negatively correlated with the endowment and utility is concave. This means that short traders default when long traders' endowment draws are low (on average), and the marginal utility of long traders' consumption is high. In contrast, the marginal utility of consumption of the short trader defaulting is low since they received a favourable endowment draw (on average), but do not have to pay if there is a large adverse price movement. This asymmetry means that higher default probabilities reduce the value of OTC derivatives.
When traders cannot default and the correlation between the contract pay-off ym,t and the endowment Am,t is equal to −1, traders can offset all endowment risk. This is equivalent to the complete markets solution to our model and is the first-best optimum.
Notes: For both panels – the welfare gains are calculated assuming no central clearing, in which case the constrained-efficient and decentralised solutions are identical; for the left-hand panel – two-sided default probability is 1 per cent; for the right-hand panel – corr(ym,t, Am,t) = −0.7
4.2 Effects of a CCP on Trade and Welfare
4.2.1 Default fund: insurance against default
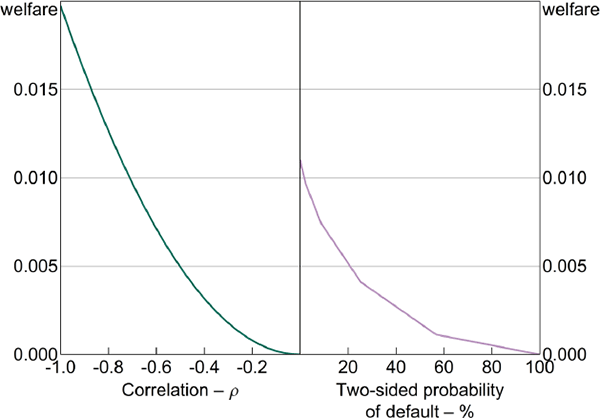
We now introduce central clearing and examine how the key parameters of our model affect welfare and allocations. Figure 5 shows the effect of increasing the fraction of trades centrally cleared, under both the decentralised and constrained-efficient equilibria – that is, increasing λm. For this comparison, the CCP only uses the lump-sum default fund contribution; we discuss the role of margin in further detail below.
The results highlight that the effect of central clearing depends on whether a decentralised or constrained-efficient solution is used. In the constrained-efficient solution, increasing central clearing monotonically increases welfare – full clearing is optimal. The effect on OTC derivative trade is relatively small.[28] This is because additional central clearing increases the fraction of contracts that are insured, and so are a better hedge. In the constrained-efficient solution prices adjust to incorporate the additional marginal cost of this insurance incurred by the CCP, and so there is no trade distortion. Central clearing is beneficial because it efficiently mutualises credit risk in the constrained-efficient equilibrium.
Notes: The CCP collects no margin; the two-sided default probability is 1 per cent; welfare is relative to no clearing
The results for the decentralised equilibrium are quite different. Increasing λm leads to a fall in social welfare and a large increase in the number of contracts traded. The reason is that, although traders privately value additional novated contracts that are free of counterparty credit risk, the value to society of these contracts is negative in the absence of any mechanism to price the additional insurance the CCP provides. When only the default fund is used to fund payouts, the marginal decision of any trader to trade more OTC derivatives fails to internalise the cost of the trader's own default on the CCP's cost of providing insurance. We refer to this as a ‘mutualisation externality’. It is similar to a moral hazard problem, where insuring an agent against risky activity can lead to the agent undertaking more of that activity.
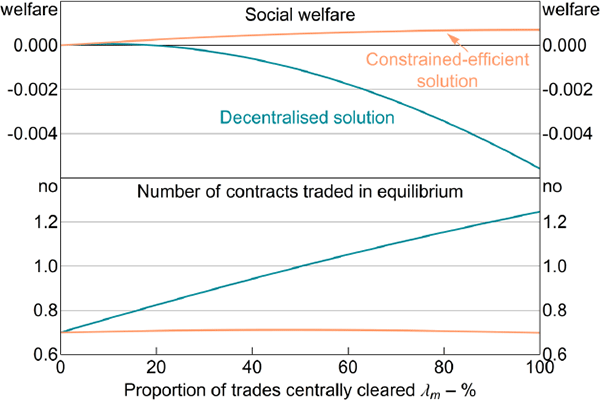
Figure 6 highlights the relationship between the effectiveness of the hedge and the social value of central clearing in the constrained-efficient equilibrium (top-left panel). A CCP is more valuable to traders when the contract is a more effective hedge – that is, when the correlation between endowment payouts and OTC derivative payouts is more negative. When the correlation is very negative, counterparty default occurs at the same time traders receive adverse endowment draws, on average. This is when the payments on the contract are most valuable and, therefore, when the CCP's insurance is most valuable.
Notes: The CCP collects no margin; for left-hand panels – two-sided default probability is 1 per cent, welfare gains are relative to the welfare of the no clearing equilibrium, given the relevant correlation; right-hand panels show welfare difference between full clearing (λm = 1) and no clearing (λm = 0)
A similar intuition underlies the probability of default (Figure 6, top-right panel). Default reduces hedge effectiveness and therefore welfare; the higher the probability of default, the greater the welfare loss. Since the CCP never defaults, it therefore reduces these welfare costs. Examining the interaction between default and the correlation in contract payouts, we see that central clearing is most valuable when the probability of default is high and OTC derivatives would otherwise provide an effective hedge against idiosyncratic risk. In this case, traders place a high value on the insurance against counterparty default provided by the CCP. In contrast, when either the probability of default is low, or OTC derivatives are only an ineffective hedge, the welfare gains from central clearing are small.
The bottom panels of Figure 6 tell the same story as Figure 5. Although the same benefits from central clearing are present in the decentralised equilibrium as in the constrained-efficient equilibrium, the cost of the mutualisation externality is much larger than these benefits. As a result, in the decentralised equilibrium, central clearing can reduce welfare, particularly when default is likely (Figure 6, bottom-right panel).
4.2.2 The mutualisation of default losses
Figure 5 showed that traders choose to trade an inefficiently large number of contracts in the decentralised equilibrium as the fraction of trades required to be centrally cleared increases. This inefficiency arises because traders do not consider the costs that their own default imposes on the CCP. These costs raise the required default fund contribution for all traders. In effect, traders are taking advantage of the asymmetry in the pay-off structure for centrally cleared contracts – traders can default, but the cost of ensuring that the CCP never defaults is mutualised.
In contrast, the constrained-efficient solution internalises the costs of traders' defaults on the CCP. The terms on the last line of Equation (27) show the difference between the pricing equation derived from the decentralised version of the model and the constrained-efficient version for the long trader in market m.[29]
This wedge, which we call the ‘mutualisation externality’, comprises:
-
The expected difference between what the CCP will have to pay the long trader when the long
trader is in the money (ym,t) and the payment the
CCP expects to receive from the long trader when the long trader is out of the
money(fm,t):
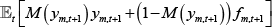 .
.
-
Any offsetting margin:
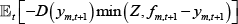 . This term reduces the loss the
CCP suffers by either: the full amount fm,t + 1 − ym,t
+1 if the loss is less than the posted margin; or Z if the margin is not
sufficient to cover the loss.
. This term reduces the loss the
CCP suffers by either: the full amount fm,t + 1 − ym,t
+1 if the loss is less than the posted margin; or Z if the margin is not
sufficient to cover the loss.
-
The marginal social value of any increase in the expected difference between payouts and
collections:
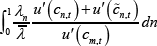 .
.
Internalising the mutualisation externality reduces the value of OTC derivatives to a trader and therefore leads to fewer contracts traded in equilibrium.
The mutualisation externality is increasing in the probability of default (Figure 7, right-hand panels). This result is intuitive – a higher probability of default increases the expected difference between M(ym,t)ym,t and (1 − M(ym,t))fm,t, and therefore increases the size of the externality. In contrast, correlation has little effect on the size of the mutualisation externality (Figure 7, left-hand panels). Although a weaker (less negative) correlation implies a slightly larger externality, the effect is negligible.
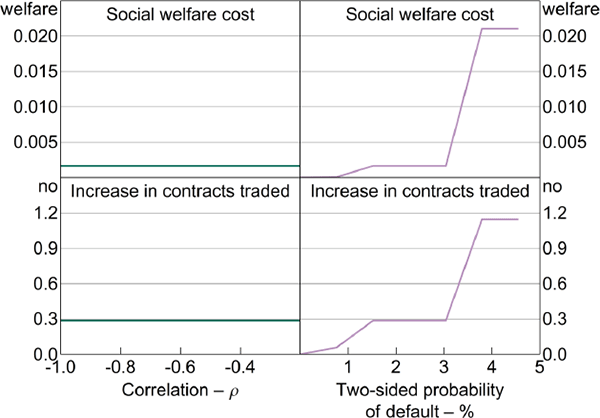
Notes: Welfare cost and the increase in contracts traded measured relative to the constrained-efficient equilibrium for the relevant parameters; for all panels – the CCP collects no margin, λm = 0.5; for the left-hand panels – two-sided default probability is 1 per cent; for the right-hand panels – corr(ym,t, Am,t) = −0.7
4.2.3 The role of margin
It is straightforward to show that the mutualisation externality could be exactly corrected by levying market-by-market state-contingent taxes on contracts. The efficient state-contingent tax would need to be set equal to the terms on the last line of Equation (27). In practice, these taxes do not exist. But CCPs do collect margin.
Margin requirements act like an implicit tax because the collateral posted to meet the requirements does not earn a return in our model. This makes margin costly because current consumption is more valuable than future consumption. Margin is also costly in reality, because the low yields on collateral-eligible assets imply an opportunity cost. However, margin requirements and taxes are not identical. With margin, traders give up resources today, but have their resources returned if they do not default, and so margin requirements affect both the cost and the pay-off structure of OTC derivatives. In contrast, a tax is never returned – it affects only the cost of trade today.
Figure 8 highlights that higher margin requirements (measured relative to the standard deviation of ym,t) induce traders to trade fewer contracts in both the decentralised equilibrium and constrained-efficient equilibrium by increasing the cost of trade. The effect is strongest in the decentralised equilibrium, which has a lot more trade absent any margin requirements. Importantly, higher margin requirements reduce the welfare gap between the constrained-efficient equilibrium and decentralised equilibrium. This is because the implied increase in the cost of trade, although not identical to an optimal state-contingent tax, does a good job of replicating its effects.
Accordingly, the overall level of trade converges from an inefficiently high private level without margin, towards the social optimal level as margin requirements are raised.[30]
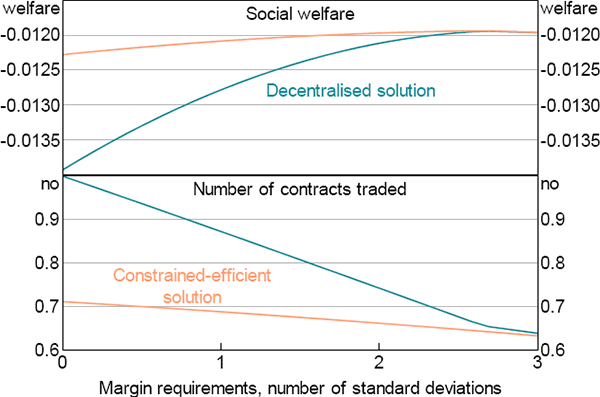
Notes: λm = 0.5, two-sided default probability is 1 per cent; decentralised welfare measure is adjusted for the initial endowment of margin; welfare is measured relative to the welfare from a constant stream of consumption equal to Ā
Figure 9 shows the margin requirements that maximise social welfare in the decentralised solution as a function of the probability of default. It implies that CCPs should set higher margin requirements as the probability of default increases, which is intuitive given that the size of the mutualisation externality increases as the probability of default increases (Figure 7).
Figure 10 highlights that, with appropriately set margin requirements, welfare in equilibria with full clearing is higher than that with no clearing for all possible correlations and default rates considered. Moreover, the welfare gain between the two equilibria is higher the more negative the correlation between the contract and endowment payouts (i.e. the more effective the hedge for a given rate of default) and the higher the probability of default (for a given contract correlation). Nonetheless, this figure does not answer the question of whether full clearing is always socially optimal, as an interior λm could potentially yield higher welfare. This is the question we now address.
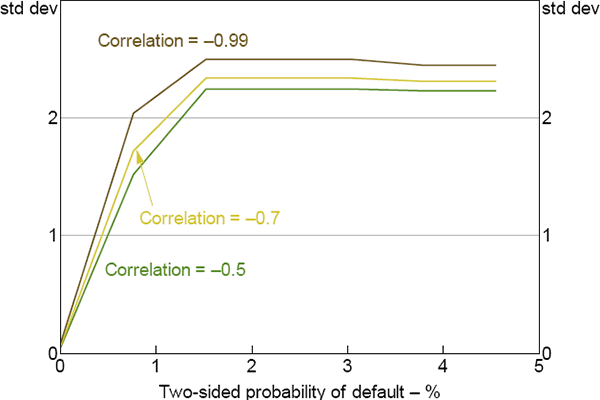
Note: λm = 0.5
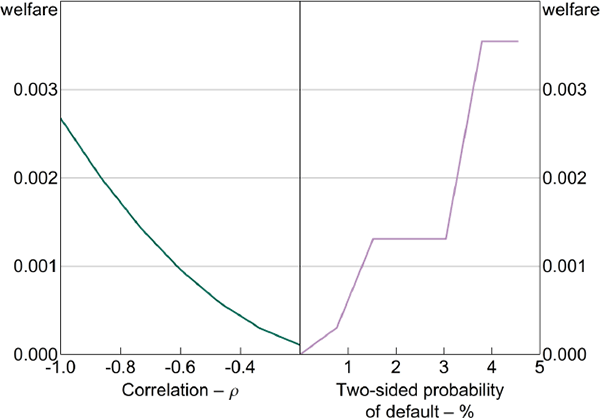
Notes: For the left hand panel – two-sided default probability is 1 per cent; for the right hand panel – corr(ym,t, Am,t) = −0.7
4.3 Optimal Central Clearing
For the optimal level of central clearing, we numerically maximise social welfare over two parameters jointly: the proportion of contracts that must be centrally cleared and required margin, which we now refer to as optimal margin. We also consider cases where margin requirements are held fixed at either zero margin, low margin (covering 90 per cent of the one-tailed moves in ym,t), PFMI margin (99 per cent of one-tailed coverage) or high margin (99.9 per cent one-tailed coverage).
Figure 11 shows the fraction of central clearing (λm) that maximises social welfare in a decentralised equilibrium.[31] Consistent with the constrained-efficient results in Figure 5, if margin requirements are set optimally, full clearing is always welfare maximising (the top panel of Figure 11). This reflects the result that optimal margin in a decentralised equilibrium can provide a good approximation of the constrained-efficient equilibrium.
On the other hand, if margin requirements are not set optimally, full clearing may be less than optimal:
- If margin requirements are set too high, full clearing will lead to too little hedging. The ‘high margin’ line in Figure 11 shows this effect: when the probability of default is low, high margin is needlessly expensive, which makes central clearing too costly relative to its insurance benefits.
- If margin requirements are set too low, the severity of the mutualisation externality will overwhelm the benefits of central clearing. This effect can be seen in the ‘ zero margin’ and ‘ low margin’ lines in Figure 11. At low default probabilities, low margin requirements are near optimal and so the welfare-maximising level of mandatory central clearing is high. But, as the probability of default rises, the mutualisation externality becomes too acute. In these cases, mandatory central clearing obligations will have the opposite of the intended effect: participants will take on too much risk by trading an inefficiently large number of contracts.
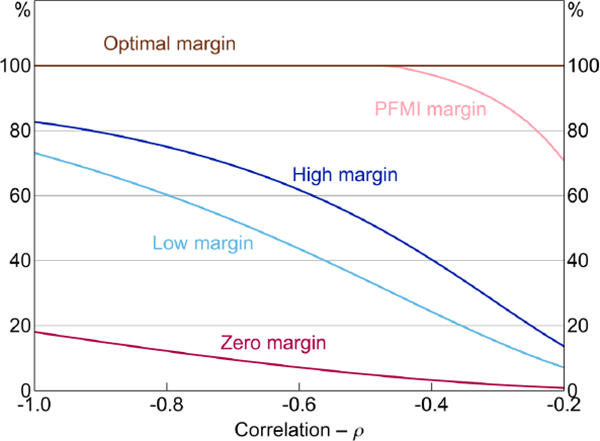
Figure 12 shows how the social welfare-maximising proportion of central clearing depends on the correlation between the endowment (Am,t) and the OTC derivatives contract (ym,t). With the exception of optimal margin, the welfare-maximising fraction of mandatory central clearing decreases as the OTC derivative becomes a less effective hedge.
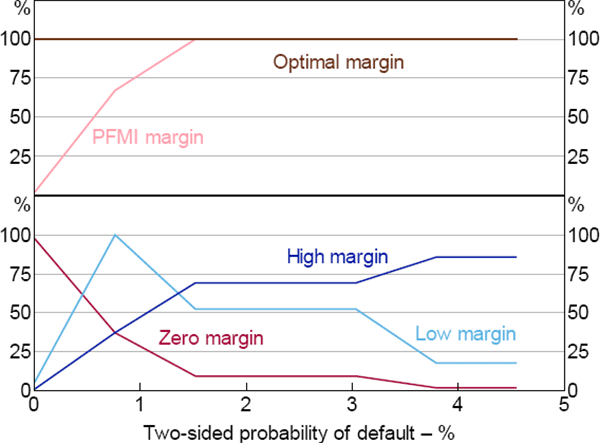
4.4 Implications and Caveats
A key implication of our findings is that the efficiency of central clearing depends on how close margin is to its optimal level. If margin requirements are set too low, the moral hazard problem embedded in central clearing can be substantial and mandatory central clearing can be very inefficient. Similarly, if set too high, margin makes trading too expensive and, thus, mandatory central clearing inefficiently reduces risk sharing in this case.
A second implication of our findings is that the case for mandatory central clearing is strongest for asset classes that are closely correlated with banks' underlying risk – for any initial margin requirements (Figure 12). To the extent that banks are the focus of OTC derivatives reforms, this observation suggests that the case for mandatory clearing requirements for interest rate, foreign exchange and credit derivatives is stronger than other asset classes. To date, policymakers have indeed focused on interest rate and credit derivatives.
Third, quantitatively our model suggests that current international standards that require CCPs to set margin to cover at least 99 per cent of one-tailed movements, or 2.33 standard deviations in our model, are very close to the optimum margin requirement in the decentralised equilibrium when the probability of default is 2 per cent or more (Figure 9). At lower rates of default, less than full clearing becomes optimal when PFMI margin requirements are applied (Figure 11).
Of course, a good deal of caution is required in drawing inference from these results to real-world policy. Our model is highly stylised and abstracts from many crucial features that policymakers must additionally consider. For example, the only costs of central clearing in the model are the mutualisation externality and the opportunity cost of the collateral posted as margin. In practice, there are many other policy-relevant costs associated with central clearing. Setting up and maintaining a relationship with a CCP is time-consuming and expensive, and requires a high degree of operational sophistication – far more so than establishing a bilateral trading relationship. For many market participants, these costs make central clearing prohibitively expensive. These costs also depend on the type and size of the market participant; our model abstracts from this type of heterogeneity. Central clearing is also liquidity intensive; not all market participants are well-suited to manage the associated costs and risks. All these factors suggest that not all participants are like those in our model.
Similarly, there may be additional reasons why not all products are suitable for clearing, which our model cannot see. For instance, although our model suggests there may be gains from mandatory clearing of foreign exchange OTC derivatives – because this asset class is likely to be correlated with banks' assets and liabilities – central clearing of foreign exchange derivatives faces technology and infrastructure hurdles that have not yet been solved. These hurdles are policy relevant, but not considered here.
Finally, our model does not consider some of the benefits of central clearing. For instance, our model says nothing about the netting or financial-stress benefits that central clearing brings about by simplifying the financial network, nor does our model say anything about the benefits from having coordinated default management. These benefits have been extensively covered in the literature, so we have not addressed them here.
Footnotes
The number of contracts increases very slightly – about 1 per cent between no clearing and full clearing. [28]
See also Appendix B. [29]
Note that the small increase in social welfare in the constrained-efficient solution reflects the effect of margin on the steady state of the economy, and not a correction in the pricing of OTC derivative contracts. [30]
We focus only on the decentralised equilibrium because traders' responses are important for the optimality of any real-world market structure reform. [31]