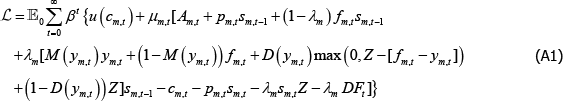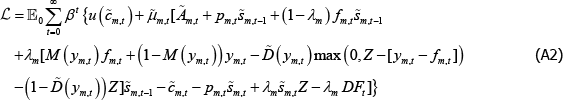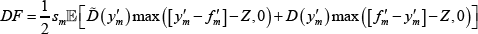RDP 2016-07: The Efficiency of Central Clearing: A Segmented Markets Approach Appendix A: Trader Behaviour and Solution Method

A.1 Lagrangians

The Lagrangian for the long trader is:

where μ_m,t is the Lagrange multiplier on the period t budget constraint for a long trader in market m. This equation is maximised by choice of c_m,t and s_m,t.

The short trader is similar:

The first-order conditions from these problems yield Equations (17) and (20) in the main text.

A.2 Numerical Methods

We solve the system by first picking a scalar s_m and then solving each pricing equation for a stationary price vector. Restricting attention to equilibria where the quantity of trade is not state contingent considerably simplifies the computational burden of the problem. We approximate the expectation on the right-hand side of the pricing equation using Gauss-Hermite numerical integration. The price vector is the discretised numerical approximation of the state-dependent price function. We use 35 quadrature nodes for both A_m,t and y_m,t, which means we have a total of 1,225 states. We use such large numbers because most of the action in our model occurs in the tails. This means that we need a large state space to ensure smooth coverage of the tails, particularly when we vary parameters like margin requirements: smaller state spaces mean that there are large discrete jumps as margin requirements or default bounds move past one of the tail quadrature nodes.

Solving the system then amounts to finding a scalar value of s_m such that price vector solutions to the two pricing equations are approximately the same. We find this value of s_m using a numerical nonlinear solver. In all cases we assume λ_m = λ for all m. This greatly simplifies the solution method, because all markets are identical. We need to solve for only one s_m, because this will be a solution for all the markets.

The equilibrium solution to our model (without collateral) is always an s_m such that the price for both agents is zero. This is consistent with real-world practice: most OTC derivatives have zero net present value when agreed on.^[32] This is an intuitive result, traders are trading the contract so that their consumption (which depends on s_m) is uncorrelated with the payoff of the contract. Because of the symmetry in long and short traders' optimisation programs, the s_m that ensures this is the case for both traders is the same (noting that ).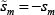

In some cases we need to evaluate integrals across all markets, for example, for the stationary equilibrium CCP default fund fee (Equation (24)). We do so by relying on the fact that draws of y_m and A_m are independent of s_m and that both y_m and A_m are independent and identically distributed and uncorrelated with other markets (i.e. corr(A_m, A_n) = 0). These assumptions allow us to use a law of large numbers such that:

which we evaluate by a Gauss-Hermite quadrature rule in the same way as outlined above.

In principle, we can also solve for a state-contingent vector for s_m, and focus on the first moment of this distribution. Numerically, this is a much more computationally demanding problem because we quickly run into the curse of dimensionality when jointly maximising welfare over λ_m and Z. Nevertheless, to see if our results are sensitive to our simpler solution method we compared the first moment of the solution with a given distribution for s_m with the non-state-contingent solution. The results are similar in this case.

Footnote

There are a few exceptions, such as market-agreed coupon interest rate swaps and standardised credit index derivatives. [32]