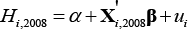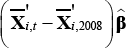RDP 2016-06: Jobs or Hours? Cyclical Labour Market Adjustment in Australia Appendix B: Composition Effects

Rather than considering all potentially relevant compositional factors individually (e.g. age, gender, industry, part-time/full-time employment), a multiple regression-based approach can be used to consider the combined effect of these variables simultaneously. This approach can be used to estimate the effect of compositional shifts in employment on the change in average hours worked between August 2008 and any given quarter since the late 1970s.

The first step is to estimate a regression using data on individual workers from the August 2008 cross-section of the LFS:

where H_i,2008 is actual hours worked per month by individual i, 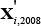is a vector of explanatory variables and β is the vector of coefficients to be estimated. The regression is weighted using the ABS's population weights. The explanatory variables include: part-time or full-time employment status (1 dummy), age group (11 dummies), gender (1 dummy), industry (18 dummies), occupation (7 dummies), marital status (1 dummy), whether the employee was born in Australia or another main English or non-main English-speaking country (2 dummies), and whether the worker is an employee, employer or self-employed (2 dummies).

The contribution of compositional change to the overall change in average hours between August 2008 and quarter t is given by

where 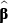is a vector of estimated coefficients from the August 2008 cross-section of the LFS 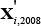and and 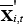are the means across individuals of the observed values in August 2008 and quarter t, respectively. This is referred to as the ‘composition effect’. While LFS micro data are not currently available on a consistent basis prior to 2008 or after 2010, 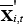is available from the published LFS employment time series data. The ‘composition effect’ measures the change in average hours that would have occurred between August 2008 and quarter t if all within-category (e.g. within-industry and within-age group) hours had remained constant at their August 2008 levels. The difference between the actual change in average hours and the ‘composition effect’ measures the effect on average hours of changes in hours within categories of employment, holding composition constant.^[19] In this paper, this is referred to as the ‘within effect’.

Footnote

This approach is equivalent to estimating a Oaxaca-Blinder decomposition between August 2008 and every other quarter t. However, rather than estimating a separate regression for every quarter in time (along with August 2008), it simply treats any difference between the actual change and the composition effect as the ‘unexplained (or within) effect’. [19]