RDP 2016-01: Measuring Economic Uncertainty and Its Effects 2. Measuring Economic Uncertainty in Australia
February 2016
- Download the Paper 1.07MB
- Data
Existing proxies for uncertainty fall into three broad categories: newspaper based; finance based; and forecaster disagreement. A brief survey of some other types of measures that have been used in the literature can be found in Appendix A.[2]
2.1 Measures of Economic Uncertainty
2.1.1 Newspaper-based measures[3]
To capture uncertainty reflected in media coverage, I follow Baker et al (2015) to construct a measure of newspaper articles that reference economic uncertainty.[4] The idea behind the measure is that information about economic uncertainty could be contained in newspaper coverage, not that media coverage causes economic uncertainty.[5]
These newspaper-based measures have a number of benefits. They capture a broad range of uncertainty (unlike, for example, finance-based measures) and are extremely timely – the search can be run daily, although I use monthly averages in this paper.
I collect data from four newspapers: The Australian; The Australian Financial Review (AFR); The Age; and The Sydney Morning Herald (SMH). Following Baker et al (2015), I search a database of newspaper articles (Factiva) for economic uncertainty-related articles. To meet the search criteria an article must contain ‘economy’ (or variants) and ‘uncertain’ (or variants) and at least one of the following terms: ‘budget’, ‘policy’, ‘legislation’ (or variants), ‘regulation’ (or variants), ‘parliament’, ‘senate’, ‘reserve bank’ or ‘RBA’. These restrictions are designed to exclude uncertainty-related articles that are not relevant to the economy and are similar to those used by Baker et al.
For each newspaper, I measure the number of articles that match the criteria relative to the total number of articles published in that month (Figure 1). The total number of articles used for the denominator includes all articles (e.g. current affairs, sports, lifestyle). The aggregate series is an equally weighted average of the individual newspaper measures.[6]
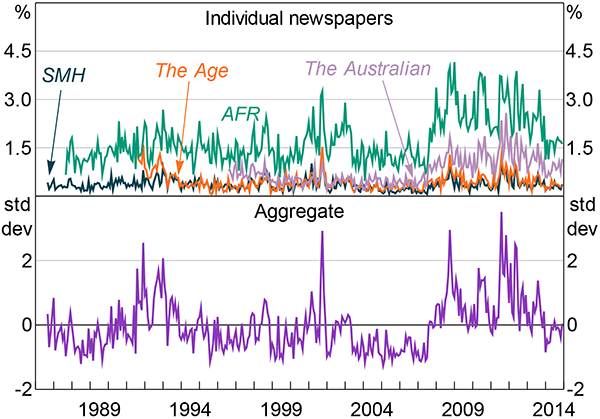
Note: The aggregate measure is an equally weighted average of the individual newspaper measures, which are first standardised to have mean 0 and standard deviation of 1 over August 1996 to December 2014
Sources: Author's calculations; Factiva
At first pass, the measures look sensible: they appear to capture major events fairly well, although they do often lag these events a little. For instance, the proportion of uncertainty-related articles in the AFR was higher in October 2008 than in September (when Lehman Brothers collapsed); the proportion in The Australian behaved similarly. These lags are partly a function of monthly averaging – Lehman Brothers collapsed in the middle of September, which means it would affect the totals for September less. But this behaviour also reflects the characteristics of the media coverage. In September, coverage focused on the immediate uncertainties for the US financial system and broad-sweeping articles about the crisis. By October, as the immediate turmoil subsided, coverage switched towards US and Australian government responses.
Consistent with the general theme of all the uncertainty proxies I review, the individual newspaper measures are highly correlated with one another (Table 1). The more business-focused newspapers – The Australian and the AFR – are most strongly correlated. These newspapers also have higher proportions of economic uncertainty-related articles, given their business focus.
| The Australian | AFR | The Age | SMH | Aggregate | |
|---|---|---|---|---|---|
| The Australian | 1 | ||||
| AFR | 0.76 | 1 | |||
| The Age | 0.62 | 0.69 | 1 | ||
| SMH | 0.51 | 0.57 | 0.76 | 1 | |
| Aggregate | 0.84 | 0.88 | 0.89 | 0.83 | 1 |
|
Notes: All correlations are significantly different from zero at the 1 per cent level; all correlations are for the period August 1996 to December 2014 because there are no data for The Australian prior to this date Sources: Author's calculations; Factiva |
|||||
There are methodological drawbacks to these types of measures. In particular, false positives are unavoidable. However, Baker et al (2015) used similar search terms for the United States and audited the results by reading through a large number of articles to check whether the articles were in fact about economic uncertainty. Although there were some differences between the machine-created and the hand-created series, the two series were strongly correlated. In addition, the error rates were uncorrelated with economic variables.
2.1.2 Finance-based measures
Stock market volatility is a commonly used proxy for uncertainty because it is available in real time and is reasonably comparable across countries. For example: Caggiano, Castelnuovo and Groshenny (2014) use it to assess the effects of uncertainty on the US economy; Bekaert, Hoerova and Lo Duca (2013) decompose it into a risk aversion component and an uncertainty component to test how monetary policy affects both; and Baker and Bloom (2013) use natural disasters and stock market volatility to assess the effects of uncertainty.
Realised volatility – measured here by the monthly average of the daily absolute percentage change in the All Ordinaries index – is one measure of stock volatility.[7] The main benefit of this measure of stock volatility is that it provides a very long time series. However, because uncertainty is necessarily about the future, forward-looking measures of stock volatility are conceptually preferable. A measure of forward-looking stock market volatility can be constructed from the implied volatility of call and put options on the ASX 200 index (Figure 2).[8] It represents the expected one-month-ahead volatility in the ASX 200. Unfortunately, data for option-implied volatility are more limited than some of the other measures I use in this paper – data are only available from 1995 – which means it does not cover, for example, the early 1990s recession.
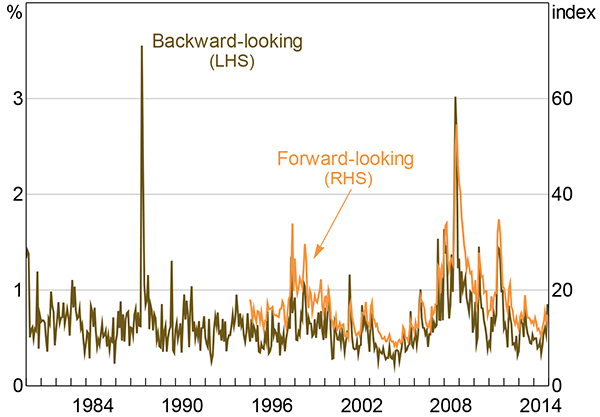
Notes: The forward-looking measure is the monthly average of daily option-implied volatility for the ASX 200; the backward-looking measure is the monthly average of the absolute value of daily percentage changes in the All Ordinaries index
Source: Thomson Reuters
The drawback of these stock volatility measures is that they are only indirectly connected to economic activity. Although company earnings are connected to economic activity, much of the short-run variation in stock prices is driven by other factors (Shiller 1981; Cochrane 2011). Although these factors may relate to economic uncertainty, the connection to economic activity is not clear. These measures are also asymmetric – increases in the measures accompany large falls in stock prices; large gains in stock prices are less common.
Another finance-based measure of uncertainty is the dispersion in analysts' forecasts for 12-month-forward earnings for ASX 200 companies. The benefit of this measure is that it is more directly connected to economic activity – corporate profits are part of GDP – than measures of stock volatility. It is also quite timely, although less so than stock volatility measures. However, it has a much shorter history than most other measures and, like other measures of forecaster disagreement, might capture disagreement, rather than uncertainty (this issue is discussed in Section 2.1.3).
The measure is calculated as the cross-sectional coefficient of variation of analysts' forecasts for each ASX 200 stock. This is then aggregated to obtain an average for all ASX 200 companies, and for sectors (Figure 3).
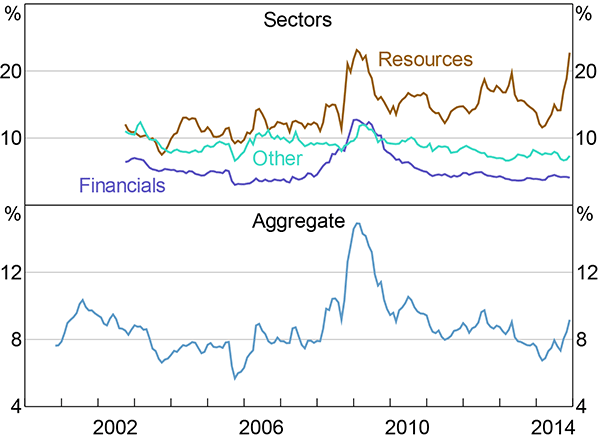
Note: Coefficient of variation on 12-month-forward earnings forecasts
Sources: MSCI; Thomson Reuters
2.1.3 Forecaster disagreement
Measures of dispersion between forecasters for economic variables can also proxy for economic uncertainty (Figure 4). Heightened economic uncertainty widens the potential distribution of outcomes; this should show up as greater dispersion among forecasters.
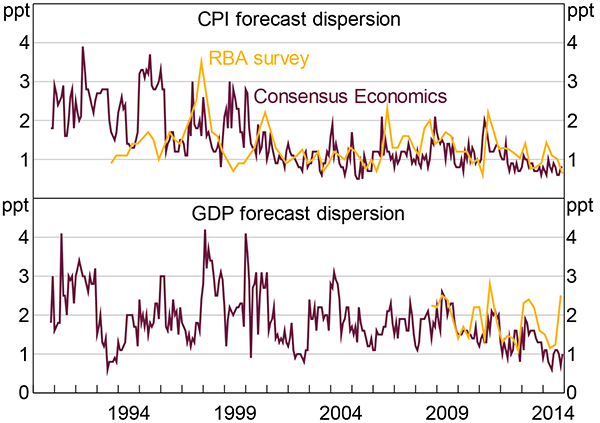
Notes: Range between highest and lowest forecast; Consensus Economics survey forecasts are for the next calendar year; RBA survey forecasts are for year-ended growth between four and five quarters ahead (depending on the date of the survey)
Sources: Author's calculations; Consensus Economics; RBA
However, an important criticism of measures of forecast dispersion is that forecast dispersion and uncertainty are not identical. Forecast dispersion might instead capture disagreement – how far forecasters are from one another – not uncertainty. Each forecaster could be extremely certain, but there could still be a high degree of disagreement (and vice versa). Some authors have argued that, in light of this distinction, forecast dispersion is a poor proxy for uncertainty (Rich, Song and Tracy 2012).
On the other hand, forecast dispersion measures are closely conceptually connected to economic activity. Moreover, these measures are timely – for instance, the Consensus Economics survey is typically conducted in the early part of the month and the responses are published shortly thereafter.
There is a reasonable degree of correlation between the different measures of forecast dispersion for which I have data, across both different surveys and different forecasted variables (Table 2). These correlations suggest that there is a common element that drives dispersion among forecasts for different economic variables.[9] There is also statistically significant correlation between the dispersion in cash rate forecasts and the dispersion in GDP forecasts, but not with the dispersion in CPI forecasts (Table 2).[10]
| RBA survey of market economists – CPI | RBA survey of market economists – GDP | Consensus Economics – CPI | Consensus Economics – GDP | Market economists' cash rate forecasts | |
|---|---|---|---|---|---|
| RBA survey of market economists – CPI | 1 | ||||
| RBA survey of market economists – GDP | 0.05 | 1 | |||
| Consensus Economics – CPI | 0.27** | 0.28 | 1 | ||
| Consensus Economics – GDP | 0.28** | 0.60*** | 0.35*** | 1 | |
| Market economists' cash rate forecasts | 0.33 | 0.41* | 0.05 | 0.43*** | 1 |
|
Notes: Range between highest and lowest forecast; Consensus Economics forecasts are for the next calendar year; RBA forecasts are for year-ended values between four and five quarters ahead (depending on the date of the survey); market economists' cash rate forecasts are for the level of the cash rate in two quarters time; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively; pairwise correlations are for the maximum available period, based on data availability (see Appendix B for details on data availability by series); all correlations are at monthly frequency except RBA survey of market economists, which is against the quarterly average of the other series Sources: Author's calculations; Consensus Economics; RBA |
|||||
A drawback of these types of dispersion measures is that outlying observations can exert a large influence, and the measures I use – based on the range – are particularly susceptible. Single contrarian forecasts can cause large increases in the range, even if the rest of the forecasts are tightly clustered. This is more of an issue because the samples of forecasters are not constant in the surveys I use. For example, Consensus Economics surveyed a particularly contrarian forecaster during the early part of 2000 who consistently forecast GDP growth roughly 2 percentage points lower than the vast majority of other forecasters.[11] This forecaster was not included in all surveys. As a result, the Consensus Economics GDP forecast dispersion measure was very volatile in early 2000 as this forecaster transitioned in and out of the survey sample. Measures of dispersion that ignore outliers – such as the interquartile range – can mitigate these issues. Unfortunately, I do not have access to data for the interquartile range.
2.1.4 Correlations between the measures
Even if each of the measures reviewed above represents a noisy signal of some true underlying process of economic uncertainty, there should be a reasonably high degree of correlation between all these measures. Table 3 shows that this is the case.
| Option-implied volatility(a) | Realised volatility | Analyst earnings forecast uncertainty (ASX 200)(a) | Proportion of uncertainty-related articles (aggregate)(a) | SMP- based measure | RBA survey of market economists – CPI | Consensus Economics – GDP(a) | Consensus Economics – CPI | |
|---|---|---|---|---|---|---|---|---|
| Finance-based measures | ||||||||
| Option-implied volatility(a) | 1 | |||||||
| Realised volatility | 0.85*** | 1 | ||||||
| Analyst earnings forecast uncertainty (ASX 200)(a) | 0.66*** | 0.45*** | 1 | |||||
| Text-based measures | ||||||||
| Proportion of uncertainty-related articles (aggregate)(a) | 0.59*** | 0.38*** | 0.45*** | 1 | ||||
| SMP-based measure | 0.05 | −0.02 | 0.09 | 0.34*** | 1 | |||
| Forecast dispersion | ||||||||
| RBA survey of market economists – CPI | 0.29** | 0.25** | 0.31** | 0.04 | −0.11 | 1 | ||
| Consensus Economics – GDP(a) | 0.11* | −0.04 | 0.13* | −0.03 | −0.03 | 0.28** | 1 | |
| Consensus Economics – CPI | 0.11* | −0.03 | 0.33*** | 0.00 | −0.01 | 0.27** | 0.35*** | 1 |
|
Notes: ***, ** and * denote statistical significance at the 1, 5 and 10 per
cent levels, respectively; pairwise correlations are for the maximum
available period, depending on data availability (see Appendix B for details on data
availability by series); all correlations are at monthly frequency except
RBA survey of market economists and the Statement on Monetary
Policy (SMP)-based measure, which are against the
quarterly average of the other series; measures with limited data are
excluded from this table Sources: Author's calculations; Consensus Economics; Factiva; MSCI; RBA; Thomson Reuters |
||||||||
The main exception is that all three measures of forecast dispersion in Table 3 are only modestly correlated with the finance-based measures of uncertainty and are uncorrelated with the newspaper-based measure. This low degree of correlation might reflect the effects of adverse shocks that reduce expected growth in ways that do not increase forecast dispersion – i.e. because forecasters agree on the likely outcome – but which are still associated with increases in uncertainty that are picked up by the other proxies. This issue of forecaster disagreement versus uncertainty is discussed in Section 2.1.3.
2.2 An Index of Economic Uncertainty for Australia
All the measures co-move and behave similarly around major events. These facts suggest that there is some underlying ‘economic uncertainty’ process. I use four of the measures to construct a monthly economic uncertainty index for Australia (Figure 5). The index tries to capture this underlying process by smoothing away the noise inherent in any particular measure. The components of the index are: economic uncertainty-related newspaper articles; forward-looking stock market volatility; analyst earnings forecast uncertainty; and GDP growth forecast dispersion.[12] I use these components because they are timely and capture a broad range across the three categories of uncertainty measures.
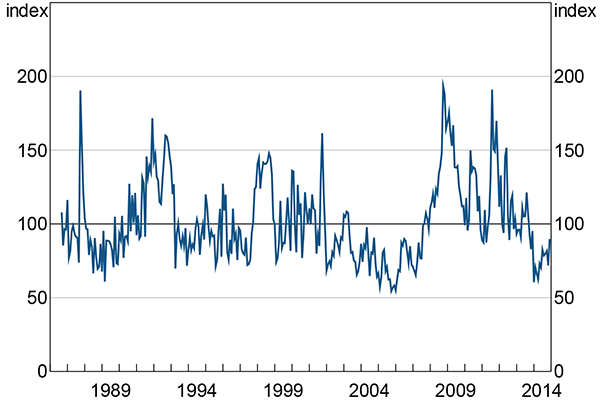
Note: For the period November 2000 to December 2014: mean = 100 points, standard deviation = 30 points
Sources: Author's calculations; Consensus Economics; Factiva; MSCI; Thomson Reuters
The index is a weighted average of the standardised components. The weights are: 50 per cent on the newspaper-based measure; one-sixth on each of the remaining three measures. I use these weights because they match those used by Baker et al (2015). Appendix C shows that the index is robust to different weights. This is unsurprising given the correlation among the measures.
I scale the index so that it has mean of 100 points and standard deviation of 30 points over the period November 2000 to December 2014. This choice is arbitrary; I pick these figures for the mean and standard deviation because they are similar to the headline index from Baker et al (2015). Over the full history, the index has a mean of 101 points and a standard deviation of 27.5 points.[13] Appendix C explains how the index is constructed and how I deal with changes in data availability over time.
Like the indices from Baker et al (2015), the index captures economic policy uncertainty through the newspaper-based component.[14] Indeed, the uncertainty-related news articles component from Section 2.1.1 is an analogue of the many country-specific economic policy uncertainty indices from Baker et al (2015). However, the index I construct captures a broader range of economic uncertainty than Baker et al's economic policy uncertainty indices because of the other components I include. In particular, I use stock market volatility and analyst earnings forecast uncertainty in place of upcoming tax code expirations and forecast dispersion for government purchases of goods and services. Comparable data for Australia do not exist for these components.
Late 2014 is a good example of the conceptual distinction between economic uncertainty and economic policy uncertainty, and why I aim for the broader concept. In late 2014, the outlook for China became more uncertain, which was associated with falling commodity prices. This type of uncertainty is likely relevant for the Australian economy, and so an index of uncertainty ideally should capture it. However, it is not the result of policy decisions by Australian agencies; indeed, the newspaper-based measure did not move around this time. Rather, the analyst earnings forecast uncertainty measure picked up this event.
Footnotes
Appendix B contains a list of the measures reviewed in this section and the time periods for which they are available. Although most of the data in this section are available daily, I use data up to December 2014. [2]
I am extremely grateful to Stephen Cupper and Sue Morris for their assistance in collecting the data used in this section. [3]
Alexopoulos and Cohen (2009) also construct a newspaper-based measure of uncertainty for the United States. [4]
Although there are plausible feedback mechanisms. [5]
I first standardise the individual newspaper measures to have mean zero and standard deviation of one over the period for which data exists for all four newspapers. Articles that are syndicated across more than one of the newspapers will be double counted under this methodology. [6]
I use the monthly average of the absolute value of daily percentage changes because it is most strongly correlated with the option-implied measure over the period for which data exists for both measures (correlation of 0.85). This is in slight contrast to Bloom (2009) and Caggiano et al (2014), who use the within-month standard deviation of daily percentage changes. However, there is little difference between the two series. I use the former measure because it helps mitigate the effect of Black Monday in 1987. The within-month standard deviation measure has a correlation of 0.84 with the option-implied volatility series, very slightly less than the series I choose for realised volatility. [7]
The forward-looking measure of Australian stock market volatility is similar to the closely watched VIX in the United States. [8]
The sample of institutions in the two surveys is similar, so the correlation between dispersion in the two surveys for the same forecast variable is perhaps less surprising. [9]
These data are only available for a relatively short period of time – since April 2009. [10]
History was very unkind to that forecast. [11]
I use GDP rather than CPI forecast dispersion in the economic uncertainty index because it is likely that there is a structural change in CPI forecast dispersion due to the RBA adopting inflation targeting. [12]
The full history is September 1986 to December 2014. [13]
As of an October 2015 revision, Baker et al focus on the uncertainty-related news articles component because it is comparable across countries. The original version of the index that I discuss is still presented as the headline monthly index for the United States on their website, policyuncertainty.com; this index is also available through a number of commercial data providers. [14]