RDP 2016-01: Measuring Economic Uncertainty and Its Effects Appendix C: Constructing the Economic Uncertainty Index
February 2016
- Download the Paper 1.07MB
- Data
C.1 The Components and Construction of the Index
Figure C1 presents the standardised components of the economic uncertainty index.
-
Stock market volatility is constructed from option-implied volatility for the ASX 200 index. Prior to January 1995, the component is constructed from realised volatility of the All Ordinaries index, measured by the monthly average of the absolute value of the daily percentage change in the All Ordinaries index. I rescale the realised volatility measure so that it has the same mean as the option-implied volatility measure over January 1995 to December 2014.
Splicing the two measures together seems reasonable because the forward- and backward-looking measures of stock market volatility line up well. The correlation coefficient between the two series is 0.85 and peaks in the two measures largely coincide. However, the backward-looking measure is more volatile than the forward-looking measure. Over the period for which data exist for both measures, the coefficient of variation for the backward-looking measure is roughly 30 per cent larger.
- Analyst earnings forecast uncertainty is constructed from the coefficient of variation – the cross-sectional standard deviation divided by the mean – of analyst earnings forecasts for ASX 200 companies.
- The uncertainty-related newspaper articles series is the proportion of articles relating to economic uncertainty in The Australian, the AFR, The Age and the SMH. I construct the aggregate series in Figure C1 by standardising the individual newspaper measures over the period for which data exists for all four newspapers to have mean zero and standard deviation of one and then taking an equally weighted average. I use an equally weighted average because I am agnostic about which papers are most influential. Whether an article is related to uncertainty is mechanically determined by a set of search criteria. Not all papers are available for the full sample.
- GDP forecast dispersion is the range between forecasts for GDP growth for the next calendar year from Consensus Economics.
Each of these components is discussed in Section 2.1.
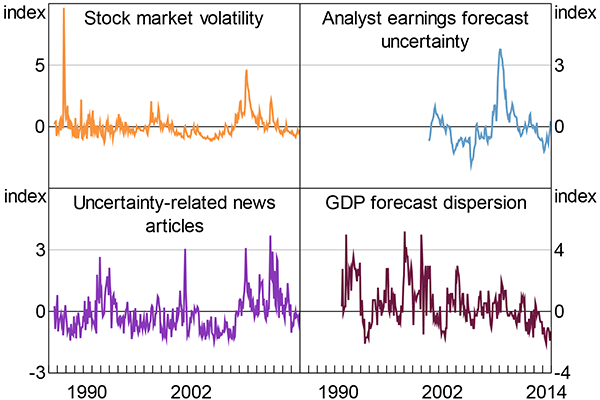
Note: For the period November 2000 to December 2014: all components are standardised to have mean 0 and standard deviation 1
Sources: Author's calculations; Consensus Economics; Factiva; MSCI; Thomson Reuters
In order to construct the index, I demean and standardise all of the components for the period November 2000 to December 2014 to have a standard deviation of one (Figure C1). I then take a weighted average of the components, with 50 per cent weight on the uncertainty-related newspaper articles component, and one-sixth on each of the remaining three components. These weights mirror Baker et al (2015). I then rescale the index so that it has a mean of 100 points and a standard deviation of 30 points for the period November 2000 to December 2014. These choices are arbitrary, and are designed to roughly match the mean and standard deviation of the US economic policy uncertainty index from Baker et al (2015).
C.2 The Three Indices That Make Up the Economic Uncertainty Index
Because the analyst earnings forecast uncertainty series is not available prior to November 2000 and the GDP forecast dispersion series is not available prior to November 1990, I use alternative indices that exclude these components for earlier periods. Each alternative index is scaled to have mean 100 points and standard deviation 30 points for the period November 2000 to December 2014.
For the period November 1990 to November 2000 I use an index that excludes analyst earnings forecast uncertainty (‘excl analyst’). This index is constructed in the same way as the preferred specification index, but with 25 per cent weights on the stock market volatility and GDP forecast dispersion components. For the period September 1986 to October 1990 I use an index that combines the uncertainty-related newspaper articles component and the stock market volatility component with weights of two-thirds and one-third respectively (‘news and volatility only’).
To construct the full-history index in Figure 5, I simply swap to the index containing more data sources as soon as it is available.
The three indices on which the overall index is based are strongly correlated (Table C1). Furthermore, the differences between the three different indices are negligible (Figure C2). The three indices are similar enough that the benefit of having the longer time series outweighs the small differences in comparability between the earlier and later specifications of the index.
| Preferred specification | Excl analyst specification | News and volatility only specification | |
|---|---|---|---|
| Preferred specification | 1 | ||
| Excl analyst specification | 0.98 | 1 | |
| News and volatility only specification | 0.95 | 0.94 | 1 |
|
Notes: Correlations are over the period November 2000 to December 2014, for which data exist for all three indices; all correlations are significant at the 1 per cent level Sources: Author's calculations; Consensus Economics; Factiva; MSCI; Thomson Reuters |
|||
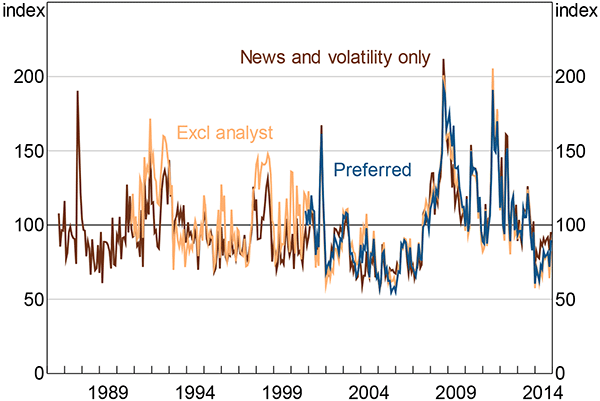
Note: See note to Figure 5
Sources: Author's calculations; Consensus Economics; Factiva; MSCI; Thomson Reuters
C.3 Different Weights
The index is robust to different weights on the components. Figure C3 compares my preferred specification to an equally weighted index and an index where the weights are determined by principal component analysis (PCA).[33] I restrict to the period after November 2000 – the period for which data exist for all four of the components of the preferred specification index. The similarity between differently weighted specifications is unsurprising given the relatively high degree of co-movement among measures of uncertainty (Section 2.1.4).
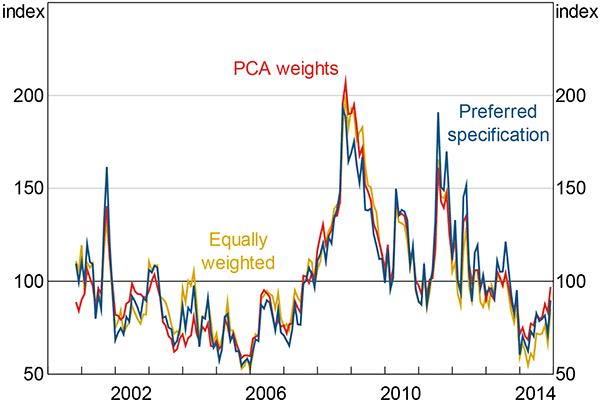
Note: See note to Figure 5
Sources: Author's calculations; Consensus Economics; Factiva; MSCI; Thomson Reuters
Footnote
The weights for the PCA weights index are: 0.3 on the newspaper-based component; 0.31 on the analyst earnings forecast uncertainty component; 0.34 on the stock market volatility component; and 0.04 on the GDP forecast dispersion component (weights do not sum due to rounding). [33]