RBA Annual Conference – 1998 Microeconomics of the Australian Labour Market John Freebairn[*]
1. Introduction
The Australian labour market is in a constant state of adjustment to external and internal shocks. Changes in aggregate demand, tastes and preferences, technology, institutions and government policies, and world trade conditions are examples of secular, cyclical and random forces for change. They induce changes in decisions of households to offer labour and acquire skills, and in decisions of firms to hire labour. Price, quantity and quality signalling mechanisms are involved in directing and co-ordinating labour market responses to the shocks. This paper reviews the literature on the underlying demand and supply functions, and the adjustment mechanisms for the Australian labour market in aggregate, and for components such as occupations, industries, skill levels, gender, age, regions and hours of work. In particular, it focuses on insights provided about unemployment and its composition.
Labour markets the world over, not just Australia, are more a fix-price or customer market than a flex-price or auction market. Sticky average wages and sticky relative wages across occupations, age etc. reflect tradition and history, long-term investment and repeat-contract relationships, endogeneity of effort, and the complex and often implicit nature of employer-employee agreements. Changes in unemployment take a part of the adjustment response to external and internal shocks to the labour market. Over the past thirty years, aggregate unemployment has varied from less than 2 per cent to over 11 per cent, and would be higher if underemployment and disguised unemployment were included. The composition of unemployment is much higher among the unskilled and new workforce entrants, and it varies across occupations, industries, regions and so forth. Understanding the underlying microeconomic causes of unemployment provides an important information resource for contemplating and assessing policy options to reduce unemployment.
Section 2 provides an overview of a sticky-wage model for components of the labour market and for the economy. Microeconomic foundations of the wage-setting, labour demand and labour supply functions are described in Sections 3, 4 and 5 respectively, along with a collation of, and assessment of, available estimates for Australia of key elasticities and shift parameters. Section 6 discusses intra-labour market reallocation mechanisms in response to shocks to the labour market. A final section draws out some implications of the paper for the aggregate level of unemployment and its composition.
2. Overview
Figure 1 provides a general framework for modelling the determination of quantity and price outcomes in the Australian labour market. It can be considered for the market as an aggregate, as in Stacey and Downes (1995), or for particular components in terms of an industry, occupation, region, skill level, age, gender, part-time or full-time, and so forth. Quantity outcomes include employment, unemployment and vacancies in terms of numbers of people and hours, and price outcomes include employer labour costs, employee disposable returns and wages. The figure enables organisation of arguments and of estimates in terms of the market-clearing mechanisms, and in terms of elasticities and variables shifting the labour demand, labour supply and wage offer curves.
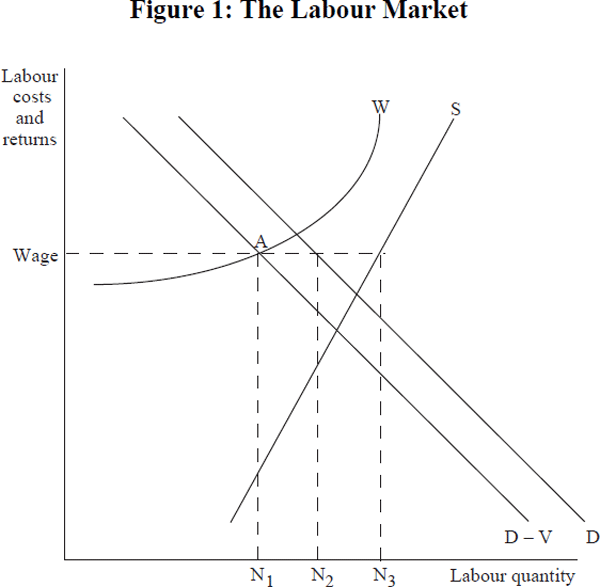
Conventional labour supply and demand curves for a particular industry, gender, skill group etc. provide basic building blocks of a microeconomic model of the labour market. S is labour supply reflecting workforce participation and hours decisions, and the choice of a particular industry, occupation etc. Labour demand is given by D reflecting employers' willingness-to-hire decisions. Since not all jobs are filled immediately because of frictional and structural adjustments, there is a certain level of vacancies V, and measured employment is recorded with reference to the D–V curve.
The wage offer curve W captures the sticky-price characteristic of labour markets. For an aggregate labour market it might be based on a Phillips curve, a bargaining model, or an efficiency wage model for example, and typically it would rise with tighter labour market outcomes. For a particular segment of the labour market, the wage offer curve for an industry, occupation, gender etc. also reflects notions of comparative wages and fairness. Institutional, political and social factors may be major explanatory forces. A key issue to be explored at the disaggregated labour market level is the elasticity of the wage offer curve with respect to the balance of labour supply and demand for particular occupations, ages etc.
Labour markets, like other markets, ultimately have to adjust to shifts in the supply and demand curves via a combination of price flexibility, quantity adjustments in terms of changes in unemployment or vacancies, or by quality changes. To illustrate, in Figure 1, for a given D and S, a high sticky wage generates a wage outcome at Wage, employment at N1, vacancies of N1N2 and unemployment of N1N3. A very much lower wage curve would have vacancies and frictional unemployment only. Given the heterogeneity of labour in terms of formal skills, experience, age, and so forth, labour markets may also adjust by raising standards or the quality of employees when unemployment is large, and reducing them when vacancies are large relative to unemployment.
The sticky-wage model illustrated in Figure 1 cautions the interpretation of recorded employment and wages for the identification of the labour demand and supply curves. Where there is substantial involuntary unemployment, as has been the case in aggregate, and for most disaggregated components of the Australian labour market since the mid 1970s, only the demand curve is identified, and strictly only the D–V curve. If the wage offer curve is below the supply and demand intersection point, as might have been the case in the 1950s and 1960s, the supply curve is identified but not the demand curve. These observations are important to the interpretation of reported econometric estimates of labour supply and demand functions.
While the partial equilibrium model of Figure 1 for a particular component of the labour market provides a useful framework for considering policy options, it is necessary to be careful with the choice of ceteris paribus assumptions. This is especially true with respect to the wage offer curve. In most, but not all, cases, shifts in the wage offer curve for a particular industry, occupation, skill group, and so forth through comparative wage mechanisms, also will affect the curve for another industry etc. Again, lower labour costs, production costs and then prices for one industry are likely to also mean lower labour costs and prices for other industries. Here, changes in comparative cost and price effects, rather than first-round absolute effects, become the point of analysis. Similarly, changes in the level and composition of aggregate demand, technology, tastes and other exogenous shocks will affect all segments of the labour market. That is, analyses of policy options towards the labour market ultimately have to consider the aggregate or macroeconomic labour market.
There are several important different price terms on the vertical axis of Figure 1. Employee labour supply responds to real returns or effective purchasing capacity, while employer demand responds to real labour costs, neither of which equals wages. Labour costs include superannuation, workers compensation, payroll tax, fringe benefits and leave allowances, and arguably complementary labour hiring, training and firing costs. The labour on-costs of superannuation, payroll tax and workers compensation, on average represent more than 12 per cent of wages, they have become more important over time, and their relative importance varies by industry, and by firm size (ABS cat. no. 6348.0). Employees are concerned about effective personal real disposable income. This includes not only wages, but also as argued by Covick (1996) a component of superannuation which is a form of deferred pay, workers compensation as a form of insurance – but for many less than a dollar, per dollar of employer on-costs – and leave allowances which provide worker utility. Income taxes and the withdrawal of means-tested social security benefits reduce disposable income, and indirect taxes reduce effective purchasing power. These tax wedges between wages paid by employees and private purchasing power gained by employees are large and highly variable according to income level, gender and family circumstances, and they have varied over time. It might be argued that general taxation revenue, income taxes, expenditure taxes and payroll taxes, fund government goods and services of value to employees. However, individual employees presumably place well below a dollar valuation on them for each labour-cost dollar siphoned off their wages as taxation. Then, wages are likely to be a poor proxy for employer costs and for employee returns due to variations over time and across individuals.
By contrast to the real labour costs of interest to employers and measures of the real effective purchasing power of interest to employees, the wage offer curves generally are set in nominal terms. However, almost always, expected inflation is an important explanatory variable, and in many aggregate labour market studies the expected price variable has a coefficient close to or equal to unity, in which case expressing the wage offer curve in terms of real wages becomes a close approximation.
3. Wage Offer Curve
The wage offer curve of Figure 1 captures the key sticky-price property of labour markets, both the inflexibility of average wages and the inflexibility of relative wages for different occupations, industries, regions, skill levels, gender, ages, hours of work, and so forth. This section explores the determinants of average wage rates and of the structure of relative wage rates in Australia. Particular attention is given to the influence of an excess or shortage of labour demand and labour supply on the average level and structure of wages.
Clearly the flex-price textbook model in which wages automatically and quickly adjust to equate labour demand and supply in each and every component of the labour market is not a useful description of the Australian labour market. Persistent unemployment for many years, differences in unemployment and vacancy rates according to age, skill level, occupation etc., and cyclical variations in the aggregate level and composition of unemployment are inconsistent with a flex-price model. On the other hand, there is some variation of relative wages, but wage flexibility is small when compared with quantity changes in the composition of the workforce and employment.
Institutional arrangements, including Australia's third-party system of arbitration tribunals, have an important bearing on wage outcomes. With a few notable exceptions, such as the wage freeze of 1982–83 and the early phases of the Accord, the tribunals set minimum wages only. While as many as 30 per cent of the workforce may be paid minimum awards, over-award payments are important components of many wage agreements. Tribunal decisions are driven by factors other than, or in addition to, labour supply and demand imbalances. For example, the 1907 Harvester case and recent Living Wage cases illustrate the key role of perceptions of a fair wage on equity criteria applied to minimum-wage setting. Settling industrial disputes is another criterion specified in the various government Acts and Regulations. But also, the tribunals are provided with considerable information on the state of the economy and labour market conditions in the submissions by advocates for employers and employees and by governments. Tribunal decisions often contain extensive reference to assessed current and anticipated labour market circumstances. That is, arbitration tribunal wage decisions are influenced by labour market conditions and also by other criteria.
Different models explaining average wages are explored in more detail in other papers, however a brief summary provides key insights useful for better understanding wage offer curves for different categories of labour. At least three model types, and associated econometric studies, to explain aggregate wage outcomes in Australia have been reported: a disequilibrium market model, Phillips curve models, and bargaining models. The underlying causal mechanisms and list of explanatory variables in the wage offer function vary with each model. However, each has a common property that some measure of labour demand and supply imbalance pushes the wage offer in the direction of labour market balance, but with the adjustment being slow and partial. That is, the wage offer curve for the aggregate labour market version of Figure 1 is upward-sloping.
A disequilibrium labour market model, for example Lewis and Kirby (1988), has an equilibrium wage determined by the intersection of labour demand and supply (with these functions driven by variables described in Sections 4 and 5), and implicitly with some allowance for frictional and structural employment. Each period, the wage adjusts only partially to the discrepancy between the previous period's wage and the equilibrium wage. Partial adjustment reflects a combination of inertia and negotiation costs, continuing contracts, and the implicit contract model carrying a preference for wage stability. Institutional changes are allowed to influence the adjustment rate, and Lewis and Kirby find the 1975–81 indexation period significantly speeded up the adjustment rate. The estimated model has satisfactory economic and statistical properties. It implies that wages slowly adjust to net changes in the excess demand (or supply) of labour.
The most popular model to explain Australian aggregate wages has been some version of the augmented price expectations Phillips curve model. Recent examples are Murphy (1992) and Stacey and Downes (1995). Increases in nominal wages are expressed as a function of expected consumer prices – often with a pre-specified coefficient of unity – labour productivity growth, and a measure of labour market slack. In early models the inverse of the unemployment rate was used, giving a wage offer curve as in Figure 1 which initially is relatively flat and then increases in slope becoming asymptotic to the labour supply curve. Since the 1970s, the unemployment measure often has been purged of the long-term unemployed, or replaced by overtime hours, so as to better reflect labour demand and supply imbalances by ‘insiders’ as opposed to ‘outsiders’. To capture hysteresis effects, a variable for the change in the unemployment rate is included. Inclusion of these modifications for the measures of labour demand and supply imbalances have been necessary to enable the Phillips curve models to have explanatory success for the 1980s and 1990s data. The addition of variables for institutional changes, including greater centralisation of the industrial relation system, particularly the Accord period of the mid 1980s and less often the indexation period of the second part of the 1970s, is found to reduce wage increases, but not always by a statistically significant amount.[1]
A third group of potential models behind the wage offer curve is a bargaining model between employers, employees, and possibly also industrial tribunals and governments. The underlying model and list of explanatory variables is somewhat ad hoc, and statistical assessment of fit is given much weight. Pissarides (1991) provides a good example. Invariably some measure of labour market pressure based on the unemployment level has a negative effect on bargained wages. Other explanatory variables include expected prices, consumer prices for employees and producer prices for employers. Relative to the Phillips curve model, the bargaining model includes variables for the opportunity return if not employed, and in particular, the level and availability of unemployment benefits and other social security support, and government taxes and charges which impose a wedge between employer labour costs and employee take-home pay. These policy variables, along with changes in the industrial relations system, are found to significantly shift the wage offer curve.
Shifting from the aggregate or average wage to individual wages, personal wages vary widely in Australia, as they do in other countries, and with similar patterns and for similar reasons. Hourly wages of those in the top decile are about three times of those in the bottom decile, and the wage distribution is approximately log normal (Norris 1986). Using ABS Income and Housing Survey data for individuals, about a half of the variation of individual wage rates can be explained by differences in formal education, age as a proxy for experience and on-the-job acquired skills, occupation, industry, region, country of origin, gender, marital status, part-time or full-time, and size of firm. Recent studies include Preston (1997) and Suruga (1998). The latter finds similar results for Australia and other countries. Differences in human capital, both in the form of formal qualifications and on-the-job training, are a major determinant of wage rates. However, in the case of formal education, there is some debate on the relative importance of enhanced productivity versus screening as the underlying causal force. The importance of industry, region and firm-size variables gives some support for the efficiency wage, compensating differentials, and exploitable monopolistic explanations of wage differences. Significant gender and country-of-birth effects on personal wages are consistent with labour market discrimination. When a firm-size variable is included among the list of explanatory variables, union membership is not a significant variable, probably because award agreements apply to non-members as well as union members and because firm size and union membership are correlated (Miller and Mulvey 1996). Impressive and comprehensive as these cross-section model estimates of the reasons for differences in wages are, about a half of the differences are unexplained, and apparently similar employees undertaking apparently similar tasks in different firms earn wage rates varying by tens of percentage points.
Time-series data on relative wage rates by industries, occupations, regions, ages and skill levels provide another perspective. Data for Australia shows considerable stability over time, but with some variation (Brown et al. 1980; Norris 1986; Withers, Pitman and Whittingham 1986; Coelli, Fahrer and Lindsay 1994; Preston 1997). Further, Australian rankings are similar to those of other countries, although the Australian wage structure is more compressed, particularly at the bottom end, relative to that of the UK and US (Norris 1986). Spearman rank correlation coefficients of wage rates by industry or by occupation for different points in time fall in the 0.7 to 0.9 interval, well above zero but less than unity. With some exceptions noted below, relative wage patterns over time in Australia, as in other countries, are stable in the sense that most changes over a year or over a decade fall within a narrow band of less than 5 per cent.
However, there are some instances of large changes in wage relativities. The premium for formal education fell by over 10 per cent during the 1970s, but since then has stabilised (Borland 1996). And relative starting salaries for graduates of different disciplines vary from year to year (Graduate Careers Council of Australia, Graduate Starting Salaries newsletter). Equal pay decisions between 1969–74 led to a 20 per cent increase in the relative pay of females to males. Earnings of juniors relative to adults rose in the early 1970s, and then declined to previous ratios. In recent years executive salaries, and those of famous athletes and artists, have grown much faster than average earnings. Sticky relative wages with a few outlying mavericks of flexibility seems a more appropriate description of relative wages in Australia, rather than a rigid relative wage structure.
The effect of arbitration tribunal decisions, including award wages, on the distribution of wages in Australia raises interesting questions. At times it is clear that the tribunals have raised lower wage rates above what they otherwise would have been. For example, the Living Wage decisions of 1997 and 1998 clearly raised minimum wages much more than wages higher in the distribution. However, these increases might reflect the restoration of long-established social norms of relative wages, or alternatively they might provide incentives to flow-on wage increases at higher levels. The stability of patterns of relative wages over time, and in comparison with other countries, suggests both the catch-up and flow-on effects operate.
There are numerous forces for stability of relative wages over time. Social and political notions of equity and fairness are strong in all countries and come under the term of comparative wage justice in Australia and pattern bargaining in other countries. Implicit contracts and internal labour markets imply relative wage stability with well respected and understood career ladders. Centralised wage-setting industrial relations systems, unions, and especially large craft and/or industry unions, and Australia's system of industrial tribunals are often thought to contribute to stability of relative wages. Yet, the same patterns of relative wages are found in countries with diverse industrial relations systems, and the system in Australia has varied over time.
Of course, a flexible wage system can generate relative wage stability under special circumstances. It is the shifts of both the demand for and supply of labour for particular industries, occupations, skills etc. which are important. For example, the very large outward shifts of the female labour supply curve (largely due to preference changes) have been matched by a very large shift in the demand for females (including that due to industry composition changes). Similarly, both the demand for and supply of skilled workers have shifted outwards in recent decades, and there have been inward shifts of the demand for and supply of traditional blue collar tradesmen. However, the probability that shifts of supply and demand curves would balance to achieve relative wage stability at high levels of disaggregation and for such a long time, must be remote. Another explanation is that one or both of the demand and supply curves for labour by industry, occupation, region, skill, time of day etc. is highly elastic. As argued in Section 4 this seems not to be the case for demand, but there may be some support for highly elastic supply curves, at least over the longer term.
To the extent that there are changes in the pattern of relative wages over time, there is mixed evidence, although growing supporting evidence, that the direction of change is consistent with demand and supply imbalances by occupation, industry, region, skill level and age. Keating (1983) employs a structural model of labour demand and supply by industry and finds statistically weak support for the hypothesis that relative wages respond positively to shifts of demand relative to supply. Applying causality tests, Withers, Pitman and Whittingham (1986) find independence between relative wage changes and relative changes in unemployment and vacancies by industries and occupations, not only for Australia but also for Britain, Sweden and the US. Yet, other studies for the US using different methodologies, report strong support for the hypothesis that relative wages respond to changes in excess demand (for example Topel (1993) for the general case, and Katz and Murphy (1992) for the case of skilled and unskilled workers). The wage curves estimated for Australia by Blanchflower and Oswald (1994), and by Kennedy and Borland (1997) show a significant negative effect of regional unemployment on individual wages after correcting for human capital, industry, gender etc. effects, and in the case of Kennedy and Borland also for local land prices. Based on seven detailed case studies of particular occupations, Blandy and Richardson (1982) conclude that wage rates adjust in a supply- and demand-equilibrating direction, but with lags and in small quantities.
Overall, notions of fairness and equity between people at any time and across time for an individual result in sticky relative wage patterns across occupations, industries, regions, ages, gender, skill level, and time of work. However, shifts in supply and demand for particular categories of labour influence relative wages in the direction of market clearance, but the relative wage response is slow and in most cases small. Institutional and policy changes have on occasions influenced relative wages. Thus, the wage curve in Figure 1 for a particular category of labour is largely positioned by the economy wage average, it has some positive elasticity, and it can lie above or below the wage that clears demand and supply.
4. Labour Demand
This section focuses on the elasticity of demand for labour and shifts of the demand curve due to changes in output, other input costs and technology for particular categories of labour classified by occupation, industry, region, gender, age, skill level, and so forth, and also for aggregate labour. Hamermesh (1993) provides an extensive review, with an emphasis on US studies, while Lewis and Seltzer (1996) provide a more specific and recent review of Australian contributions.
Labour demand typically is modelled as a firm decision, and usually from a neoclassical perspective. Under a right to manage rule,[2] firms take wages and other input costs as given, and with knowledge of their product demand (represented by the price for perfect competition and the demand curve where there is market power), firms choose employment to maximise returns, or at least to minimise production costs for a given output. Extrapolating the firm model to an industry level, and especially to an aggregate economy level, requires careful consideration of realistic price and general equilibrium constraints. In particular, as observed in the previous section, wage changes for one part of the labour market in most cases are matched to a large extent by changes in wages for all other types of labour.
Lower labour costs – not just wages but also on-costs of superannuation, workers compensation and payroll tax, and hiring, monitoring and firing costs – are expected to increase employment through at least three mechanisms: factor-mix substitution per unit of production to reduce costs; product-mix substitution to reflect changes in comparative advantage; and lower production costs through to lower prices and sales increases.
In the short run, the firm labour demand curve is given by its marginal revenue product curve, and in the long run, there are greater opportunities to substitute labour for capital, energy and material inputs. The elasticity of factor substitution is the key production function or technology factor determining the elasticity of labour demand. Most econometric estimates of production, cost and profit functions find evidence of significant elasticities of substitution between labour and capital, with many being close to unity. Where time lags are allowed in the specification – and this is not often the case with production and cost functions – significant adjustment lags exceeding two years are found. In practice there are price-change recognition lags, then lags to make and implement decisions to change production methods, and there are adjustment costs, and much capital, in particular, has a productive life of several years. Then, cost minimisation by firms, industries and the economy leads to substitution of labour for capital if labour costs fall, but this response takes some time. Factor substitutability varies with firms, industries and different types of labour implying different labour demand elasticities for different industries and categories of labour.
In most textbook models of labour demand, at least by firm and by industry, lower wages have an output-expanding effect. That is, lower wages reduce production costs, and the more so, the more important are labour costs in total costs. Competition leads to these cost reductions reducing product prices and at the lower price more output is sold, and hence more employment is required. This effect is larger the more elastic is product demand. If wages fall only for a particular industry, and remain constant for others, the wage-driven output effect on employment may be important. However, the reality of the Australian labour market, as in other countries, is that wage changes, up or down, generally flow across the economy to all industries.
Consider then the extreme, but still close to reality, case where wages move proportionately across the economy. Here, the product-substitution effect comes into play.[3] Lower wages will reduce costs, and in turn prices, more for labour-intensive goods and services than for labour-extensive products. In turn, the mix of products produced and consumed will shift in favour of labour-intensive goods and services, and the more so, the more elastic the substitutability of final demand. These substitutions will increase aggregate employment and change its composition. Output and employment in capital-intensive industries, and aggregate employment in occupations and skills used relatively intensively in these industries facing a comparative disadvantage may actually fall. Conversely, lower labour costs lead to expansion of output and employment in labour-intensive industries. Clearly, the product-mix substitution responses will involve time and adjustment lags leading to a more elastic labour demand response over the longer term than the short term.
The indirect effects of labour costs on aggregate economic activity and then on aggregate labour demand are unclear. From a supply-side perspective, with floating exchange rates, it is likely that lower labour costs across the economy, per se, will not alter the absolute competitiveness of the economy since any initial gains will be eroded by a currency appreciation. From a demand-side perspective, wage changes can redistribute income. Most estimates of the aggregate labour demand elasticity are less than unity (Table 1 and Hamermesh 1993) meaning that lower wages also reduce aggregate wage income. But, at the same time, capital income rises, and some of this will be spent. But some may be saved. Higher domestic savings, via the balance of payments equation, means a lower draw on foreign capital inflow and an inducement for the currency to depreciate to expand net exports to restore an equilibrium. Then, given the reality of very sticky relative wage patterns, wage reductions are unlikely themselves to have much effect on the level of aggregate economic activity. That is, the main driving forces behind employment responses to wage changes are factor-substitution effects and product-mix substitution effects, and both will involve lagged responses.
| Authors | Type of model | Data and estimator | Explanatory variables | |
|---|---|---|---|---|
| Labour cost elasticities | Other variables | |||
| Lewis and Kirby (1988) | Disequilibrium demand, supply and partial adjustment | 1967(3)–1987(1) FIML | SR = −0.07 LR = −0.78 | Real GDP, trend (productivity), industrial relations |
| Russell and Tease (1991) | Single equation, partial adjustment | 1969(3)–1987(4) OLS | SR = −0.11 LR = −0.61 | Real GDP, trend (technological change) |
| Pissarides (1991) | Labour demand, supply and wages | 1966(3)–1986(2) IV | SR = −0.23 LR = −0.79 | Cyclical effects (competitiveness, fiscal stance, monetary stance), capital stock, real interest rate |
| Stacey and Downes (1995) | Neoclassical firm investment, employment and pricing | 1971(1)–1995(1) ECM | SR = −0.11 LR = −0.84 | Real output, labour productivity |
| Note: SR denotes short run, LR denotes long run. | ||||
A potentially interesting issue is whether structural changes since about 1980 in the Australian economy have altered the elasticity of demand for labour. Under the Australian Settlement, until about 1980, product markets were heavily insulated from competition by tariffs, quotas and other government industry policies, and extensive government ownership and operation of business enterprises. Pressure for employers to respond to higher labour costs by economising on labour were dulled. Cost-padding by monopolistic industries was widespread, and offsetting government assistance was often sought and received. Changes in the 1980s and 1990s have brought more competitive product markets, and arguably also a more competitive labour market. The economy is closer to the competitive model on which the foregoing labour demand analysis is based. It therefore seems reasonable to hypothesise that labour demand elasticities have increased in later years and that the lags have shortened as part of the response to a tougher and more vigorous competitive economy.
Output changes have significant and large effects on employment of different categories of labour and of all labour. Long-run elasticities at the firm, industry, economy, occupation, skill level, gender etc. depend on economies of scale. With most industries exhibiting linear technology, a unitary elasticity of employment with respect to output follows; and for increasing (decreasing) returns, the elasticity would be less (greater) than unity.
The short-run response of employment to outcome changes is muted when compared with the long run. For all types of labour, there are adjustment lags associated with recognition of output changes and the time required to implement employment changes. These lags explain why employment shows up as a lagging indicator. Second, because of the importance of fixed costs associated with the hiring, training and firing of labour, employers smooth out cyclical fluctuations of employment relative to output and sales cycles. This smoothing effect is more important for more highly skilled and specialised labour than for lower skilled labour because fixed costs are relatively more important for the former. For similar reasons, overtime hours, casual employment, and the use of contract labour is pro-cyclical. Then, the link between output and employment involves lagged responses and it varies across different types of labour.
The effects of technological change, and of productivity growth generally, on the composition of employment demand are many and require consideration of second-round effects in a general equilibrium context. Over recent decades, technological change has had a labour-saving bias (see for example Bureau of Industry Economics (1986) for manufacturing), and it has tended to favour the use of skilled relative to unskilled labour (Aungles et al. 1993). To the extent that the bias of technological change is an endogenous response to the relative importance of different cost components (Dixon and McCombie 1991), it is reasonable to expect past patterns to continue into the future. For a given level of firm, industry and employment output, technological changes of the type experienced tautologically mean lower aggregate employment and a change in the employment composition away from unskilled towards more skilled employees. However, this first-round or impact effect of technological change on employment is only the first of a longer sequence of effects.
Productivity growth has important second-round effects on prices, incomes and in turn on the level of employment and its composition. Most industry-level productivity growth is passed on as lower prices (Lowe 1995). The lower prices lead to expanded sales for the industry and for other closely related industries providing inputs and further processing outputs. In due course, employment in these industries increases. For given nominal incomes, lower prices following productivity change mean higher real incomes. Expenditure of the higher income increases demand and output, with products with higher income elasticities gaining more, and again employment rises to provide the extra production. Alternatively, that portion of productivity benefits passed on as higher wages or as higher returns to capital, against fixed output prices, directly expands real income and in turn further employment increases. The second-round flow-on effects of productivity growth generate additional employment overall via increases in aggregate real income and expenditure, and also they have employment-composition effects. The products with high income elasticities are favoured, as are the types of labour used intensively by the industries experiencing the productivity improvements.
Institutional changes in the industrial relations system seem unlikely to independently affect labour demand over and above indirect effects on labour costs and on productivity. Regulatory changes affecting the conditions of hiring, worker conditions and firing directly change labour costs for different types of employees – for example, full-time versus part-time. The type of industrial relations system is often argued to have an influence on relationships between employers and employees as it affects the adoption of new technology, work practices and management practices that drive the pace of productivity growth.
Econometric estimates casting light on labour demand functions can take different forms. They include estimates of production, cost and profit functions from which demand parameters can be derived, and direct estimates of labour demand functions. For Australia there are a number of production function studies which provide estimates of the key elasticities of factor substitution. Most of the direct labour demand functions reported for particular industries and for the economy are of the form:
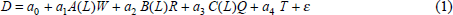
where D is employment, variously measured as persons or hours worked, W is a measure of real labour costs, variously measured as weekly earnings and unit labour costs, R is a measure of alternative real input costs, Q is a measure of output – usually industry or economy GDP as relevant – T is a time trend to measure technology, and A(L), B(L) and C(L) are lag functions. In practice most studies have imposed a more restricted Koyck lagged adjustment process rather than the flexible forms suggested in Equation (1).
Several studies have used a model of the form in Equation (1) to estimate demand for labour by industry using data for the 1960s, 1970s and early 1980s. Symons (1985) estimates the manufacturing elasticity of labour demand at −0.21 in the short run (quarter) and −0.91 for the long run, and also finds complementarity of labour with materials. A number of studies of labour demand in the agricultural sector are collated in Evans and Lewis (1986), with a new study by Lewis (1987), with estimates of the demand elasticity between −0.2 and −0.5 in the short run, and −0.5 and −1.3 in the long run. Phipps (1983) estimates demand equations for eight broad industry groups using annual data. Not all industry demand elasticities are estimated to be significantly different from zero, the largest significant estimates are around −0.5, and Phipps emphasises that elasticities vary according to industry. Given that output is included as an explanatory variable, and a predetermined one at that, the elasticity response captured by these industry studies reflects factor-substitution effects.
In the industry labour-demand studies, output and technology variables are found to be important. In most cases, a long-run output elasticity of unity cannot be rejected. A significant negative coefficient on time is consistent with labour-saving technology, and the estimated coefficient varies across industries.
Estimates of an aggregate or economy demand for labour function of the type in Equation (1) make useful comparisons with the foregoing industry-demand studies, and in particular they provide some evidence of changes in labour costs inducing changes in the mix of goods and services with different labour intensities being produced. Table 1 summarises some details and results of studies by Lewis and Kirby (1988), Russell and Tease (1991), Pissarides (1991) and Stacey and Downes (1995). They differ in terms of the underlying analytical model, the sample period, and the estimation technique, yet they reach similar findings about the main determinants of aggregate labour demand and about elasticities.
In terms of the underlying model of aggregate labour demand, Russell and Tease use a single equation, Lewis and Kirby have a disequilibrium model of labour demand and supply with partial adjustment of both wages and employment to equilibrium levels, Pissarides has a three equation model to explain labour demand, labour supply and wages, while Stacey and Downes use a representative-firm neoclassical model to explain investment, employment and prices. The estimable labour demand equation is some specific form of Equation (1), with Pissarides using a number of macroeconomic policy settings rather than GDP. Lewis and Kirby, and Stacey and Downes allow for endogeneity of wages in their estimation, while the others treat wages as a predetermined variable. Stacey and Downes use an error-correction model to avoid possible problems of spurious regression.[4] All studies use quarterly data, but with different sample periods.
Labour costs are estimated to have a significant negative effect on aggregate labour demand. There are lags of two years or more for the full response. Estimates of the long-run elasticity of demand, which is a constant-output demand elasticity because real GDP, or the macroeconomic determinants of real GDP, appear as predetermined variables in the estimated demand equations, vary from −0.6 to −0.8.[5] The aggregate labour demand elasticity estimates of Table 1 appear high when considered in comparison with most of the constant-industry-output demand elasticities discussed above and against the labour for capital substitution elasticity of unity or less found in most production function studies. One way of reconciling these differences is that the aggregate demand elasticity estimate includes product-mix substitution effects as well as factor-mix substitution effects. Then, across the economy, labour cost increases, as generally occurs (Section 3), not only induce substitution of capital for labour in producing any particular good or service, but also induce substitution of capital and other factor-intensive goods and services for labour-intensive products.
The four studies in Table 1 estimate that output has both trend and cyclical effects on aggregate labour demand. While the long-run point estimates of the output elasticity are less than unity, in most cases they are not significantly less than unity. For all the studies, output changes have a lagged effect on aggregate employment, consistent with fixed costs and with adjustment lags.
Technological change, in all cases represented by a simple time trend, has a negative effect on employment of around 1 per cent per year. Since output is a predetermined variable in the estimated labour demand functions reported in Table 1, they do not directly allow for the second-round effects of productivity growth to higher incomes and more employment.
Consider next the demand for different categories of labour, for example by gender, skill level, age or hours. Changes in relative labour costs, again not just wages but also on-costs, for one type of labour relative to others, in theory, have substitution and scale effects. A rise in the relative price of labour type i, say females, relative to labour type j, males, would lead to substitution of males for females to minimise costs. This substitution effect would be larger, the larger the elasticity of substitution of labour types i and j. There also would be a scale effect associated with an overall increase in labour costs leading to some substitution of capital for labour. The substitution and scale effects reinforce each other for the particular type of labour for which relative labour costs rise (or fall), and they work in opposite directions for other labour types. For those other labour types the net employment effect is ambiguous. There may be additional scale effects associated with changes in relative costs of particular categories of labour altering the mix of industry output. A rise in relative labour costs of labour type i will erode the comparative advantage of industries which use labour type i relatively intensively, in comparison with other industries which use relatively little of labour type i.
Unfortunately not a lot is known about the magnitude of elasticities of substitution between labour categorised by gender, age and skill level. Hamermesh (1993) finds some important areas of consensus, but many mixed results on magnitudes. Intra-labour, or labour type i for labour type j, substitutability should be considered as part of a production or cost function system with capital, and not as a system separable from capital. For skilled labour, substitutability with capital is low and in some cases complementarity is estimated, whereas high levels of substitutability between capital and low-skilled labour are estimated. Similarly, substitutability of capital is greater for production workers when compared with professionals and managers. A range of estimates, often with large standard errors, have been reported for the elasticity of substitution between high-skilled and low-skilled labour. Overall, Hamermesh concludes that the own-wage elasticity for low-skilled workers is greater than the elasticity for high-skilled workers as a consequence of the different substitution elasticities. It is likely that the Hamermesh assessment, which is based mostly on US studies, would apply to Australia, but that type of analysis has yet to be undertaken.
Estimates of elasticities of substitution for different categories of labour in Australia are few. Gregory and Duncan (1981) find a low value of 0.3 between males and females, with much of the response due to industry-composition changes rather than because of male for female substitution in providing a particular product. Lewis (1985) estimates high elasticities of substitution (up to 4) between youth and adult workers, but also notes the data were not entirely satisfactory and the estimates had large standard errors.
A related area of recent research on the demand for particular types of labour has been the study of the effects of higher minimum wages on employment of the low skilled in particular, and of other employment. Card and Krueger (1995) analysed a number of natural experiments in which increases in US minimum wages were implemented with different timings in different states of the US. Using a difference in differences approach to attempt to remove the effects of other demand forces, they find the minimum wages increases had a negligible adverse effect, and in some cases a positive effect, on employment of the low skilled. This negligible own-wage elasticity effect contradicted conventional expectations and elasticity estimates obtained from time-series studies.
Not surprisingly, the Card and Krueger studies, and related assessments for the UK generated controversy. Symposia in the Industrial and Labor Relations Review (July 1995), Economic Journal (May 1996) and the Australian Economic Review (June 1997) give some flavour of the debate. Several areas of criticism have been levelled against the negligible to positive employment response of employment to higher minimum wages. Welch (1995) is critical of the Card and Krueger data in terms of the use of telephone interviews, broad questions, and some properties of the data. Hamermesh (1995) doubts the natural experiment, arguing that since the move to higher wages was promulgated some years before, a part of the adjustment already was implemented. The before and after wage change interval of seven months suggests only short-term responses, not long-term responses, involving capital for labour substitution are captured. Also, industry-mix effects are not captured. Finally, the absence of a convincing theoretical rationale for a positive demand elasticity is a concern; a monopsony model based on informational imperfections and a model with a shock increase to efficiency have been advanced but not well supported.
For Australia there have been two sets of natural experiments which also suggest a low elasticity of demand for particular types of labour. The 20 per cent increase in relative wages for females in the early 1970s had no discernible effect on the gender composition of employment and unemployment (Gregory and Duncan 1981). Even though structural shifts in labour supply and demand by gender also were at play, these trend effects were also in play in the 1960s before, and in the late 1970s after, the policy-induced push for wage equality across the sexes. A second set of experiments concerns the large wage subsidies (up to 60 per cent of wages) for the long-term unemployed as part of the 1994 Working Nation policies. Certainly many long-term unemployed did enter these programs, consistent with a downward-sloping demand curve, and there was some reduction in employment of others (Chapman 1997). The temporary nature of the subsidies and their targeting to the more disadvantaged employees, real or perceived, as well as usual concerns about ceteris paribus, makes it difficult to draw implications about the magnitude of elasticities.
Overall, there is a dearth of convincing and robust estimates of the own- and cross-prices elasticities of demand for Australian labour disaggregated by gender, age, skill level and occupation.
5. Labour Supply
This section considers the elasticity of supply and key shift variables of the labour supply function S in Figure 1 for different ages, gender, skill levels, occupation, industries, and types of work. The review articles by Kenyon and Wooden (1996), and Borland (1997) cover the issues and Australian empirical studies in detail. Labour supply represents the outcome of decisions affecting participation in the workforce, hours of work, investment in human capital and effort level.
The individual and family work versus leisure choice model provides the underlying model of participation and hours of work decisions as a function of returns, income and demographic variables. Simpler static models focus on a single period, and others take a life-cycle perspective. Killingsworth (1983) and Woodland (1984) provide reviews. Labour returns, which involve not just market wages but also losses due to taxation and means-tested social security benefits which vary widely in their effects across people and also have varied over time, have an ambiguous net effect on labour supply because of income and substitution effects pushing in opposite directions. Alternative sources of income, including household wealth, spouse income, access to social security benefits and superannuation, and the costs of looking after children, have a negative effect on labour supply.
Almost as an empirical observation (see more below), the encouraged/discouraged worker effect has been found to be a major determinant of labour supply, at least over the economic cycle and particularly of the decisions to participate or not by married women, youth and older workers. Lower unemployment, or increases in the employment to population ratio, are associated with higher participation rates, ceteris paribus. In a sense they imply a higher probability of actually obtaining a job. In principle, this effect could be embraced in the work versus leisure model by using expected wages on entry, that is, the market wage times the probability of gaining a job, but the empirical task in measuring the probability is a formidable one.
Tastes, attitudes and social preferences clearly have had very large trend effects on labour supply decisions in Australia. These effects have been especially important for the rising participation rate of married females in the 1960s, 1970s and 1980s. Changes in preferences, in part, lie behind the shifts in the supply of labour by both sexes and by younger and older ages for part-time work and work outside the nine to five, Monday to Friday time interval.
A number of econometric studies using cross-section and time-series data support the descriptive and explanatory usefulness of the work versus leisure choice model of workforce participation and hours of work decisions, and they provide insights on the labour supply elasticity for different demographic groups. However, considerable caution is required in interpreting the results of published studies using cross-section data, including those of Apps, Killingsworth and Rees (1996), Lambert (1991), Miller and Volker (1983), Ross (1986), Ross and Saunders (1993) and Woodland (1987). In the Australian context, post 1970, involuntary unemployment has been extensive for most disaggregated categories of labour, as well as for the aggregate, so that measured employment used in cross-section studies lies inside the labour supply curve (A in Figure 1). Time-series studies using the workforce (employment plus unemployment) are less affected by the identification problem. Data limitations mean that most cross-section studies have not included variables for discouraged worker effects, or they have included a crude proxy for aggregate unemployment which is the same for individuals and families in different circumstances. To the extent that the omitted discouraged worker effect variable and the included wage variable are positively correlated,[6] reported cross-section study estimates of the labour supply elasticities are biased upwards. None of the reported cross-section or time-series studies fully allows for both taxation and means-tested social security benefits in measuring the net returns from work. For those using the market wage as a proxy variable for incentives to work, it is a poor proxy because tax and social security differ widely over time and across different individual and family circumstances.
Even granted the foregoing concerns with reported econometric studies of Australian labour supply, some results seem fairly robust and consistent with studies of other countries. The elasticity of labour supply is relatively low, and in many cases not significantly different from zero, for males and for women with full-time, high-paying jobs (Apps, Killingsworth and Rees 1996; Borland 1995). For older males, low education levels (which proxies for low wage and job opportunities, and maybe also tastes) and the availability of alternative income, whether it be private income, including superannuation, or access to social security benefits, both contribute to lower participation (Woodland 1987). For married women, the elasticity of labour supply, representing both participation and hours of work decisions, is significantly positive, but with a wide range of estimates driven by different models, data and estimation procedures and in some studies with values exceeding unity (Apps, Killingsworth and Rees 1996; Lambert 1991; Miller and Volker 1983; Ross 1986). However, because of specification problems noted above, these estimates are likely to be biased. Female participation in these studies is found also to vary with other family income, with education, with the number of young children, and with region and country of birth.
In a number of time-series studies (Borland 1995; Dixon 1996; Dowrick 1988; Stricker and Sheehan 1981) significant discouraged worker effects are found for both sexes and all age groups whereby changes in the unemployment rate, or of the unemployment to population ratio, shift the labour supply curve. Most studies assume symmetry of response with estimates that an increase in employment of one job induces about 0.4 people into the workforce. Dixon finds evidence of an asymmetric response of about 0.75 for increases in jobs and 0.3 for decreases in jobs. Borland finds that most flows out of the workforce come from unemployment rather than employment. Gregory (1991) asserts that much of the increase in female employment, and to a lesser extent male employment, comes from new entrants rather than from unemployed persons. In terms of overall explanatory power, the encouraged worker effect, or shifts in the labour supply curve, are found to be more important than the wage effects, or movements along the curve, in explaining variations of labour supplied.
Changes in labour quality stem from formal education, mostly for job entrants, and on-the-job training of employees. The human capital model captures the investment processes involved. The model predicts that education and training, and hence a more skilled workforce, increase with the premium of wages for skilled people relative to those unskilled, lower opportunity costs of foregone work and lower tuition fees. Numerous Australian studies have estimated real rates of return of around 10 per cent for secondary and tertiary education (Blandy and Goldsworthy 1975; Chapman 1977; McNabb and Richardson 1989; Miller 1982). Further, the inverse relationship between years of education and unemployment, perhaps more accentuated in the 1980s and 1990s, both increases the gross return from education and reduces the opportunity cost of study. Because of supply constraints on government-provided tertiary education, the supply curve of educated labour is not identified, and this factor lies behind the disappointing econometric results found by McCormack (1992).
No studies have been found on labour supply by occupation, industry and region, and this is not surprising because of data limitations. For occupations and industries, unemployment data refers only to those who last had a job in a particular industry or occupation, but not for those who want to enter or want to change, and thus the workforce by industry or occupation is measured poorly. The stickiness of relative wage patterns described in the previous section provides little information with which to estimate labour supply to industry i (or occupations or regions) as a function of returns in i and other industries (or occupation or region). The prevalence of changes in recruitment and promotion standards further complicates the estimation of labour supply by industry, occupation and region. It would be surprising if the elasticities of labour supply by industries and occupations were not high.
Considerable circumstantial and anecdotal evidence indicates that labour supply by occupation, industry and region shifts with employment prospects. The dominance of the encouraged/discouraged worker effect noted above for workforce participation and hours decisions would seem even easier to follow when choosing between industries, occupations and firms. Students in choosing areas of study regularly ask ‘what type of job can I expect?’ and they are avid consumers of data on unemployment rates and job advertisements by discipline area in making their choice of area of study.
6. Intra-labour Market Reallocation
In any year and over time there are large reallocations of labour between industries, occupations, regions, gender, age and skills, part-time and full-time, and by hours of work (see ABS data and for a summary, EPAC (1996)). There have been large secular changes, there are cyclical changes, and in some cases seasonal changes in the composition of employment. The changes across industries etc. are lubricated by even larger gross flows between different labour states. In any month, gross flows between employment, unemployment and not in the labour force are between 100,000 persons and 150,000 in each direction (ABS cat. no. 6203.0). For those with a job, in any one year between 20 per cent and 25 per cent changes their job, and for those who change, 40 per cent move to another industry, 30 per cent to another occupation, and 15 per cent move interstate or overseas (ABS cat. no. 6209.0). This section evaluates the co-ordinating mechanisms used in the Australian labour market to allocate and reallocate workers to different jobs in response to changes in aggregate income, buyer preferences, technology, trade, worker preferences and other shocks.
Three mechanisms, or a combination, may be used to co-ordinate the allocation of jobs to industries, occupations, regions, gender, age, skill level, time of day, part-time and full-time. These are price, quantity and quality adjustments. Necessarily, supply and demand imbalances have to be accommodated in some way. All three seem to play a role in altering the composition of Australian employment and in co-ordinating reallocations driven by external shocks.
In flexible-price markets, price changes are the co-ordinating mechanism to drive reallocations in response to changes in demand and supply. For different categories of labour, whether they be by occupation, age, gender, location, part-time versus full-time etc., relative wages would rise for those categories where demand expands relative to supply or where vacancies as a measure of excess demand rises, and relative wages would fall for these categories where supply expands relative to demand or where unemployment as a measure of excess supply rises. The required relative wage change will be greater the more inelastic the demand and supply curves for each category of labour. The evidence canvassed in Section 3 is that relative wages are sticky in Australia, as in other countries, and most, but not all, evidence is consistent with the hypothesis that relative wages move slightly and slowly in the directions suggested by changes in excess demand. That is, changes in relative wages contribute to the intra-labour market co-ordination task.
However, unemployment, and quite wide variations in unemployment by category of labour, means relative wage changes are less than those of a flexible-price market. ABS data indicates differences in unemployment rates by age and skill level, by occupation and industry, by region and by gender. These differences in many cases are long-term phenomena, for example higher unemployment among youth and the low skilled. There are some cyclical patterns, for example, more volatility for the young and for particular occupations. On other comparisons, there are swaps over time, for example, lower unemployment rates for males as compared with females were reversed in the 1980s.
Quantitative signals usually play a key allocative role in fix-price markets, and this seems to be the case for the composition of employment and the workforce, especially on the supply side. Industries, occupations, skill levels, hours of work categories etc. with high and rising employment and/or with high vacancies and low unemployment draw potential employees towards them and away from labour categories with low and declining employment and/or with low vacancies and high unemployment. In formal model terms, the labour supply curve for different components of the labour market shifts with measures of employment growth and the length of vacancy and unemployment queues.
Labour force participation rates for youth, married women, and older (aged 55 and over) workers are especially sensitive to quantitative signals (Borland 1995; Dixon 1994; Dowrick 1988; Woodland 1987, for example). The case studies in Blandy and Richardson (1982) provide evidence for particular occupations. There is much anecdotal evidence that decisions of children and their families on secondary and tertiary education, including about the period of study and area of study, are influenced as much by perceived relative chances of gaining a job as by the relative wages for jobs gained. Given the compelling evidence of the significant and large influence of quantitative signals to workforce participation decisions, and the anecdotal evidence for education and occupation choice decisions, it seems very likely that quantitative signals are important in co-ordinating labour market reallocations by occupation, industry, region, skill level and hours of work.
Changes in labour-quality decisions to induce reallocations of the workforce can operate along several dimensions. These include variations in the required skills, background and experience of staff to be recruited, loosening or tightening the criteria and their application for promotion, and changes in other work conditions. With internal labour markets, the principal response of employers to expanding (falling) labour demand is not to increase (reduce) wages but to increase (reduce) recruitments and accelerate (delay) some promotions. Access to ‘good’ jobs with career ladders, opportunities for on-the-job training and some security of tenure, and for jobs generally have to be rationed in some way, and the rationing task rises with the overall pool of unemployed. With wages held nearly fixed, other rationing criteria have to be used. One option is to ration by skill level as judged by formal education and work experience. In these circumstances, credential creep is one symptom of the use of qualitative job rationing. These circumstances also provide opportunities for employers to discriminate at little cost by, say, gender, socioeconomic status or race.
There is both hard and anecdotal evidence of the use of quality adjustments affecting employment and unemployment levels in Australia. Clearly the skill composition of the employed workforce has increased, and those with low skills are disproportionately represented among the unemployed. Aungles et al. (1993) attribute part of the increase in skills of those employed to changes in industry composition, part to changes in the occupational mix in each industry, and part to higher skills within each occupation. The industry mix and occupational mix effects probably can be explained largely by product-demand changes and by technology. While some of the higher skill mix within occupations may be attributed to technological change, much of it might be attributed to credential creep.
Disproportionately high unemployment rates among those with less formal education, and for migrants from a non-English speaking background, and the lower employment probabilities for the long-term unemployed, have at least two potential explanations. One is the screening idea and the use of qualitative allocation methods described above. The second possible explanation is the low marginal productivity of these potential employees, absolutely and relative to others, against Australia's relatively high minimum wages. While I am unaware of attempts to evaluate the relative importance of the two options, and in fact, it is unclear how such an assessment could be conducted, it would be a surprise if there was not some role for each explanation.
Whether the high levels of unemployment among those with low skills, real or perceived, are due primarily to low productivity relative to labour costs, or to credential creep or discrimination, has important policy implications. If the latter explanations are dominant, faster economic growth will be effective in soaking up the unemployed as artificially inflated credential standards are lowered. By contrast, if low productivity relative to labour costs is the principal causal force, policy options will have to consider a combination of lowering labour costs and increasing the productivity of the unemployed as well as raising aggregate real output.
7. Conclusion
Conventional microeconomic foundations of household decisions on labour supply and of firm decisions on labour demand are useful in analysing the composition of employment and unemployment by industry, occupation, region, gender, age, skill level, hours of work and so forth. Sticky but not rigid relative wages mean that quantity adjustments, mostly unemployment but sometimes vacancies, and quality adjustments in skill and experience levels used in hiring and promotion are important labour market responses to changes in demand and supply. Price, quantity and quality changes are involved in co-ordinating labour market adjustments to changing circumstances.
The limited number of econometric estimates of direct and cross-price elasticities of demand and supply for different categories of labour generally confirm the directions of effects predicted by microeconomic theories. However, different studies report a wide range of elasticity magnitudes and often with large standard errors. Measures of output and technological change have significant effects on demand. Output and factor price changes influence demand with lags necessary to effect changes in factor input mixes and changes in product mixes. The extent of credential creep and discrimination in rationing jobs in the face of unemployment queues and sticky wages is an area ripe for further study. The chances of finding a job as signalled by unemployment and vacancy rates, and probably also by required skills, influence workforce participation decisions, and these quantity and quality signals affect the choice of occupation, industry, education, time of work. The magnitudes of effects of quantity and quality signals on labour supply responses by labour market segment require more work.
Unemployment by industry, occupation, region, gender, skill, age and so forth reflects slow demand growth relative to supply growth and labour costs held above the equilibrating level. In addition, new entrants to the workforce, including youth and migrants, take much of the brunt of trend and cyclical changes in demand and supply. Also, credential creep in the face of overall unemployment helps concentrate unemployment among those with low skills, including the young, migrants from non-English speaking backgrounds, older retrenched people with limited formal education, and the longer-term unemployed.
Footnotes
I am grateful for the comments of Guy Debelle, Robert Dixon and Chris Worswick, but absolve them of any errors and misinterpretations. [*]
An interesting question arises for the near future as the Australian industrial relations system moves more toward enterprise bargaining and to individual contracts. Calmfors and Driffill (1988) suggest superior wage-inflation outcomes for either extreme of a highly centralised or highly decentralised industrial relations system when compared with a mixed system. [1]
There are some labour models in which wages and employment are jointly determined by firms, including the monopsony model and some union-bargaining models. However the practical relevance of these model situations to Australia seems limited. [2]
These effects seem not to be considered in the extensive survey by Hamermesh (1993). [3]
There is some uncertainty about the time-series properties of the variable entering a time-series demand equation of the form of (1). Different sample periods and tests give mixed results as to whether some or all of the variables are I(0) or I(1), and in the latter case whether the variables are cointegrated. See, for example, Lewis and MacDonald (1993). [4]
Interestingly, the lower demand estimate of Russell and Tease takes a higher value of −1.04 when their equation is re-estimated with data to 1997:Q4. [5]
ABS data on wage rates and unemployment for occupations and level of formal education imply a strong inverse relationship between the wage rate and the unemployment rate. Topel (1993) reports a strong inverse relationship for the US. [6]
References
Apps, P., M. Killingsworth and R. Rees (1996), ‘On the Specification of Labour Supply and Household Production Models’, Australian National University Working Papers in Economics and Econometrics No. 300.
Aungles, P., L. Deardon, T. Karmel and C. Ryan (1993), ‘Through a Rear-view Mirror Darkly: Occupational Change, 1971–1986’, Australian Bulletin of Labour, 19(2), pp. 97–113.
Blanchflower, D. and A. Oswald (1994), The Wage Curve, MIT Press, Cambridge, Massachusetts.
Blandy, R. and A. Goldsworthy (1975), ‘Private Returns to Education in South Australia’, in J. Niland and J. Isaac (eds), Australian Labour Economics: Readings, Sun Books, Melbourne, pp. 191–205.
Blandy, R. and S. Richardson (1982), How Labour Markets Work, Longman Cheshire, Melbourne.
Borland, J. (1995), ‘Male Labour Market Participation in Australia’, Journal of Industrial Relations, 37(4), pp. 587–609.
Borland, J. (1996), ‘Education and the Structure of Earnings in Australia’, Economic Record, 72(219), pp. 370–380.
Borland, J. (1997), ‘Changes in the Supply of Labour in Australia’, in Changing Labour Markets, Productivity Commission, AGPS, Melbourne, pp. 19–44.
Brown, W., J. Hayles, B. Hughes and L. Rowe (1980), ‘Occupational Pay Structures Under Different Wage Fixing Arrangements: A Comparison of Intra-occupational Pay Dispersion in Australia, Great Britain and the United States’, British Journal of Industrial Relations, 18(3), pp. 217–230.
Bureau of Industry Economics (1986), Manufacturing Industry Growth: Causes, Effects and Implications, AGPS, Canberra.
Calmfors, L. and J. Driffill (1988), ‘Centralisation of Wage Bargaining and Macroeconomic Performance’, Economic Policy, 6, pp. 13–61.
Card, D. and A. Krueger (1995), Myth and Measurement: The Economics of the Minimum Wage, Princeton University Press, Princeton, New Jersey.
Chapman, B. (1977), ‘The Rate of Return to University Education for Males in the Australian Public Service’, Journal of Industrial Relations, 19(2), pp. 146–157.
Chapman, B. (1997), ‘Labour Market Programs’, in Changing Labour Markets, Productivity Commission, AGPS, Melbourne, pp. 177–189.
Coelli, M., J. Fahrer and H. Lindsay (1994), ‘Wage Dispersion and Labour Market Institutions: A Cross Country Study’, Reserve Bank of Australia Research Discussion Paper No. 9404.
Covick, O. (1996), ‘Regulation and Labour Market Flexibility’, in Changing Labour Markets, Productivity Commission, AGPS, Melbourne, pp. 197–217.
Dixon, R. (1996), ‘Apparent Asymmetries in the Relationship Between the Participation Rate and the Employment Rate in Australia’, University of Melbourne, Department of Economics Research Paper No. 522.
Dixon, R. and J. McCombie (1991), ‘Biased Technological Change in Australian Manufacturing’, in C. Hamilton (ed.), The Economic Dynamics of Australian Industry, Allen and Unwin, Sydney, pp. 63–78.
Dowrick, S. (1988), ‘Labour Supply Trends and Prospects for Australian Unemployment in the Medium Term’, Australian National University Centre for Economic Policy Research Discussion Paper No. 188.
Economic Planning Advisory Commission (1996), Future Labour Market Issues for Australia, Economic Planning Advisory Commission Paper No. 12, AGPS, Canberra.
Evans, S. and P. Lewis (1986), ‘Demand, Supply and Adjustment of Farm Labour in Australia’, Australian Economic Papers, 25(47), pp. 236–246.
Gregory, R. (1991), ‘Jobs and Gender: A Lego Approach to the Australian Labour Market’, Economic Record, 67(supplement), pp. 20–40.
Gregory, R. and R. Duncan (1981), ‘Segmented Labour Market Theories and the Australian Experience of Equal Pay for Women’, Journal of Post-Keynesian Economics, 3(3), pp. 403–429.
Hamermesh, D. (1993), Labor Demand, Princeton University Press, Princeton, New Jersey.
Hamermesh, D. (1995), ‘Comment’, Industrial and Labor Relations Review, 48(4), pp. 835–838.
Katz, L. and K. Murphy (1992), ‘Changes in Relative Wages, 1963–1987: Supply and Demand Factors’, Quarterly Journal of Economics, 107(1), pp. 35–78.
Keating, M. (1983), ‘Relative Wages and the Changing Industrial Distribution of Employment in Australia’, Economic Record, 59(167), pp. 384–397.
Kennedy, S. and J. Borland (1997), ‘A Wage Curve for Australia?’, Australian National University Centre for Economic Policy Research Discussion Paper No. 372.
Kenyon, P. and M. Wooden (1996), ‘Labour Supply’, in K. Norris and M. Wooden (eds), The Changing Australian Labour Market, Economic Planning Advisory Commission Paper No. 11, AGPS, Canberra, pp. 15–38.
Killingsworth, M. (1983), Labor Supply, Cambridge University Press, Cambridge, England.
Lambert, S. (1991), ‘An Analysis of the Labour Supply Behaviour of Female Sole Parents in Australia’, PhD thesis, Murdoch University.
Lewis, P. (1985), ‘Substitution Between Youth and Adult Workers in Australia’, Australian Economic Papers, 24(44), pp. 115–126.
Lewis, P. (1987), ‘Short Run Factor Substitution in the Sheep and Beef Industries’, Australian Journal of Agricultural Economics, 31(3), pp. 266–272.
Lewis, P. and M. Kirby (1988), ‘A New Approach to Modelling the Effects of Income Policies’, Economics Letters, 28(1), pp. 81–85.
Lewis, P. and G. MacDonald (1993), ‘Testing for Equilibrium in the Australian Wage Equation’, Economic Record, 69(206), pp. 295–304.
Lewis, P. and A. Seltzer (1996), ‘Labour Demand’, in K. Norris and M. Wooden (eds), The Changing Australian Labour Market, Economic Planning Advisory Commission Paper No. 11, AGPS, Canberra, pp. 39–52.
Lowe, P. (1995), ‘Labour Productivity Growth and Relative Wages: 1978–1994’, in P. Anderson, J. Dwyer and D. Gruen (eds), Productivity and Growth, Reserve Bank of Australia, Sydney, pp. 93–134.
McCormack, D. (1992), ‘An Analytical Examination of Youth Labour and Education’, Labour Economics and Productivity, 4(1), pp. 19–44.
McNabb, R. and S. Richardson (1989), ‘Earnings, Education and Experience: Is Australia Different?’, Australian Economic Papers, 28(52), pp. 57–75.
Miller, P. (1982), ‘The Rate of Return to Education: Evidence from the 1976 Census’, Australian Economic Review, 15(3), pp. 23–32.
Miller, P. and C. Mulvey (1996), ‘Unions, Firm Size and Wages’, Economic Record, 72(217), pp. 138–153.
Miller, P. and P. Volker (1983), ‘A Cross-section Analysis of the Labour Force Participation of Married Women in Australia’, Economic Record, 56(164), pp. 28–42.
Murphy, C. (1992), Access Economics Murphy Model, Access Economics Pty Ltd, Canberra.
Norris, K. (1986), ‘The Wages Structure: Does Arbitration Make Any Difference?’, in J. Niland (ed.), Wage Fixation in Australia, Allen and Unwin, Sydney, pp. 183–201.
Norris, K. (1996), The Economics of Australian Labour Markets, Longman Cheshire, Melbourne.
Phipps, A. (1983), ‘Australian Unemployment: Some Evidence from Industry Labour Demand Functions’, Australian Economic Papers, 22(41), pp. 333–344.
Pissarides, C. (1991), ‘Real Wages and Unemployment in Australia’, Economica, 58(229), pp. 35–55.
Preston, A. (1997), ‘Where are We Now with Human Capital Theory?’, Economic Record, 73(220), pp. 51–78.
Ross, R. (1986), ‘Analysis of the 1980 Sydney Survey of Work Patterns of Married Women’, Economic Record, 62(178), pp. 325–337.
Ross, R. and P. Saunders (1993), ‘The Labour Supply Behaviour of Sole Mothers and Married Mothers in Australia’, Australian Economic Papers, 32(60), pp. 116–133.
Russell, B. and W. Tease (1991), ‘Employment, Output and Real Wages’, Economic Record, 67(196), pp. 34–45.
Stacey, G. and P. Downes (1995), ‘Wage Determination and the Labour Market in the Treasury Macroeconomics (TRYM) Model’, paper presented at the 24th Conference of Economists, Adelaide.
Stricker, P. and P. Sheehan (1981), Hidden Unemployment: The Australian Experience, Melbourne Institute of Applied Economic and Social Research, Melbourne.
Suruga, T. (1998), ‘Australia: Wage Differentials’, in T. Tachibanaki (ed.), Wage Differentials: An International Comparison, MacMillan, London, pp. 173–209.
Symons, J. (1985), ‘Employment and the Real Wage in Australia’, in P. Volker (ed.), The Structure and Duration of Unemployment in Australia, Bureau of Labour Market Research Monograph Series No. 6, AGPS, Canberra, pp. 77–88.
Topel, R. (1993), ‘What Have We Learned from Empirical Studies of Unemployment and Turnover?’, American Economic Review, 83(2), pp. 100–115.
Welch, F. (1995), ‘Comment’, Industrial and Labor Relations Review, 48(4), pp. 842–849.
Withers, G., D. Pitman and B. Whittingham (1986), ‘Wage Adjustment and Labour Market Systems: A Cross-country Analysis’, Economic Record, 62(179), pp. 415–426.
Woodland, A. (1984), ‘Microeconomic Modelling of Labour Force Participation in Labour Supply: A Theoretical Overview’, in A. Kaspura (ed.), Labour Force Participation in Australia, Bureau of Labour Market Research Monograph Series No. 1, AGPS, Canberra, pp. 95–118.
Woodland, A. (1987), ‘Determinants of the Labour Force Status of the Aged’, Economic Record, 63(181), pp. 97–114.