RDP 2022-04: The Unit-effect Normalisation in Set-identified Structural Vector Autoregressions Appendix A: Derivations for Bivariate SVAR
October 2022
- Download the Paper 2,225KB
A.1 Sign restrictions on impulse responses
This appendix derives the identified sets for the impulse responses to a unit shock under the sign restrictions on impulse responses presented in Section 3.
In the absence of any identifying restrictions, the identified set for (the matrix of impact impulse responses) is
and the identified set for A0 is
The impact response of the second variable to a shock that raises the first variable by one unit is
Consider the sign restrictions that the impulse response of the first variable to the first shock is non-negative and the impact response of the second variable to the first shock is non-positive , plus the sign normalisation Under this set of restrictions, is restricted to lie within the following set:
There are two cases to consider depending on the sign of . If the second set is empty. The first set is equivalent to
This set of inequalities implies that the identified set for is
which lies within the interval The impact response of the first variable to the first shock is The lower bound of the identified set for is negative and the upper bound is positive, so zero lies within this identified set and attains its maximum of one. The upper bound of the identified set for is therefore . The lower bound is attained at one of the end points of the identified set for and therefore satisfies
where: the second line uses the fact that arctan is an odd function and cos is an even function; and the third line uses the fact that cos is increasing over Since arctan is an increasing function, it follows that:
This identified set excludes zero. Since is strictly increasing in over the interval its lower and upper bounds are attained at the end points of the identified set for . Plugging the end points of the identified set for into the expression for yields the identified set for :
which is bounded.
Similarly, if is restricted to lie in the set
The second inequality implies that so the last inequality never binds. The identified set for is therefore
The upper bound of the identified set for is negative. is therefore strictly increasing over the identified set for , and the bounds of the identified set for are attained at the end points of the identified set for :
If is restricted to the set
The first set implies and the second implies so The expression for the identified set for when therefore also applies when . as approaches from above. is strictly increasing over the identified set for , so the upper bound for the identified set for is obtained by evaluating at the upper bound of the identified set for . Consequently,
A.2 Sign restrictions on impulse responses to multiple shocks
If we additionally impose the sign restrictions that and the parameter is restricted to lie within the following set:
Using working similar to that in Appendix A.1, the identified sets for and are given by:
As in the case where there are sign restrictions on the impulse responses to the first shock only, the identified set for includes zero when and the identified set for is unbounded.[24] In the case where , the additional sign restrictions tighten the identified set. In particular, the upper bound is now strictly less than zero (and is a differentiable function of , as discussed in Section 3.2.1).
A.3 Alternative parameterisation
Consider an alternative parameterisation of the bivariate model that directly imposes the unit-effect normalisation: where ,
Let and The structural parameters and reduced-form parameters are related via . Eliminating and from the system of equations yields a single equation in (H12, H21):
Solving for H21 as a function of H12 (using the quadratic formula) yields:
Figure A1 plots the two solutions. Under the sign restrictions and the identified set for (H12, H21) lies in the lower-right quadrant. When (Panel A), the identified set for H21 is bounded. When (Panel B), the identified set for H21 is unbounded, so unbounded identified sets may also arise when the unit-effect normalisation is directly imposed.
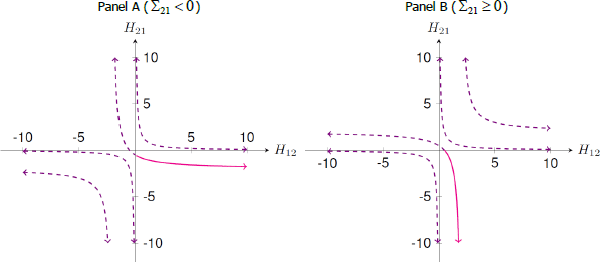
Notes: This figure depicts the solutions to Equation (A19) assuming that and The part of the solution set depicted in the lower-right quadrant of each panel represents the identified set for (H12, H21) under the sign restrictions
A.4 Magnitude restrictions
In addition to the sign restrictions considered in Section 3 and Appendix A.1, consider the restriction that for some Under this set of restrictions, is restricted to lie within the set:
The second set is always empty, since and cannot hold simultaneously when The identified set for is empty if since for all .
If , the first set is equivalent to
The last inequality never binds and the identified set for is
which is contained within the interval is strictly increasing over this interval, so the bounds of the identified set for are attained at the end points of the identified set for . The identified set for is therefore
The lower bound of this identified set, can be expressed as[25]
which converges to as approaches zero from above. The derivative of with respect to is
In the limit as approaches zero from above, this derivative approaches , which implies that the lower bound is extremely sensitive to small changes in when is close to zero.
A.5 Bounds on the FEVD
The FEV of y1t is and the contribution of to the FEV of y1t is The FEVD of y1t with respect to is therefore . Consider imposing the restriction that for some in addition to the sign restrictions considered in Section 3 and Appendix A.1. Under this set of restrictions, is restricted to lie within the following set:
When the first set is equivalent to
The inequalities and never bind and the identified set for is
which is contained within the interval is strictly increasing over this interval, so the bounds of the identified set for are attained at the end points of the identified set for . The identified set for is therefore
The lower bound of this identified set, , can be expressed as
The lower bound converges to as approaches zero from above. The derivative of with respect to is
In the limit as approaches zero from above, this derivative approaches , which implies that the lower bound is extremely sensitive to small changes in when is close to zero.
To summarise, under the additional restriction on the FEVD, the identified set is bounded; in the absence of this restriction (or as converges to zero from above), the identified set is
However, as in the case where the normalising impulse response is directly bounded away from zero, the lower bound of the identified set is sensitive to the choice of , particularly for small values of ; the derivative of the lower bound tends to as approaches zero from above. Setting to some small positive number to rule out an unbounded identified set for will therefore yield an identified set that is highly sensitive to the choice of