RDP 2021-01: The Role of Collateral in Borrowing 4. The Repo and Unsecured Markets' Reactions to Stress
January 2021
- Download the Paper 1,785KB
The paths of aggregate activity in the repo and unsecured markets diverge after the shock to market-wide stress. When the TED spread rises following the Lehman Brothers default, the unsecured market remains relatively flat (Figure 3, left panel). In contrast, the repo market expands, with the pick-up in activity moving roughly in line with the TED spread.[8] The aggregates from the 2006 placebo sample demonstrate that these patterns are particular to 2008 (Figure 3, right panel); this is examined formally in Section 5. Mancini et al (2016) find that stress generated negative correlations in trading volumes across the European repo and unsecured markets. The data in Figure 3 show a similar pattern. The cross-market correlations in the 2008 and 2006 samples are −0.36 and 0.46, respectively.
The Australian repo market expansion is consistent with the resiliency documented in US and European repo markets against high-quality securities (Copeland, Martin and Walker 2014; Mancini et al 2016), and in contrast to the tightening observed in US repo markets against private collateral (Gorton and Metrick 2012). Using the terminology of Dang et al (2015), collateral in the Australian market remained information insensitive.
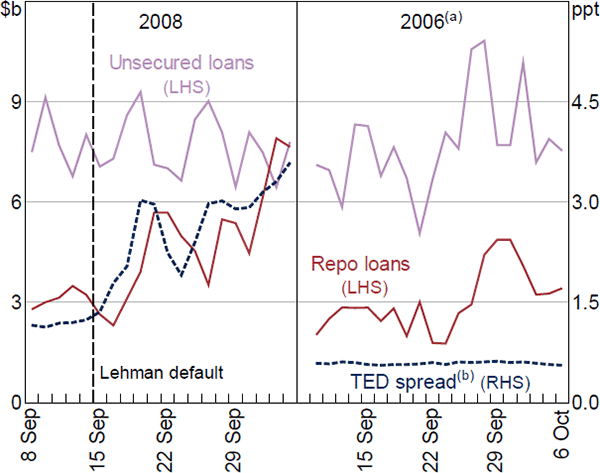
Notes:
(a) Monday 2 October 2006 was a public holiday, loans outstanding taken from the previous business day
(b) Lagged one day to account for time zones
Sources: ASX; Authors' calculations; Federal Reserve Bank of St. Louis; RBA
4.1 Heterogeneity across Borrowers
Previous research establishes that unsecured borrowers react heterogeneously to stress, and that repo and unsecured markets respond differently in aggregate (see Section 1.1). In this section we fill the gap between these sets of findings: how does borrower heterogeneity differ between repo and unsecured markets? The results show that borrower default risk plays a stronger role in the unsecured market, while borrower collateral holdings are more important in the repo market.
First the difference in reactions is visualised by plotting unsecured borrowing against repo borrowing for sub-samples of interest (Figure 4). Each scatterpoint represents the demeaned log borrowing of a bank on a given day in the repo (X-axis) and unsecured (Y-axis) markets, excluding banks that did not borrow in both markets.[9] A positive relationship indicates that banks are spreading their fluctuating liquidity needs across both markets. A negative relationship suggests that they are substituting between the two markets, on any given day concentrating their borrowing in only one.
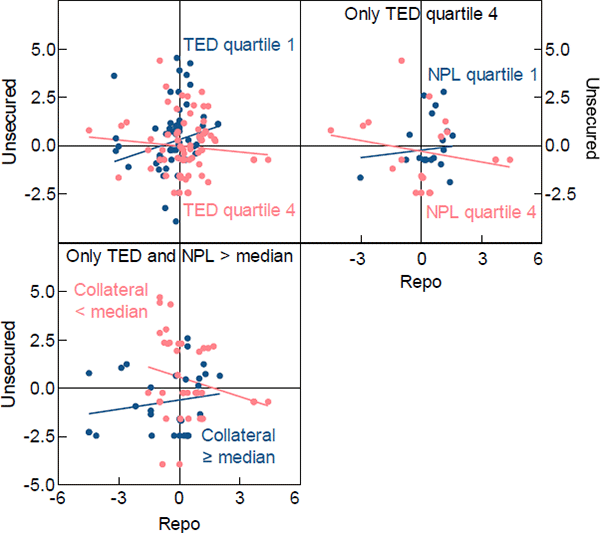
Notes: Natural logarithm of borrower-day-market level observation in AUD millions plus one, with borrower-market mean subtracted; fitted lines for sub-samples using OLS
Sources: ASX; Authors' calculations; RBA
The slopes of the fitted lines, each representing particular subsets of days and borrowers, fit the following description. First, on high-stress days banks face tighter borrowing constraints, which generates greater cross-market substitution than on low-stress days (top-left panel). Second, on high-stress days, these constraints are more likely to bind for riskier borrowers (top-right panel). Third, among the riskier borrowers, it is those with the most collateral that are most capable of substituting across markets (bottom-left panel).[10]
Our empirical strategy controls for potentially confounding factors in these relationships. One of these factors is that counterparties are not randomly matched with respect to the characteristics we examine. We demonstrate this with a modification of specification (1) that examines whether interactions between borrower and lender characteristics explain interbank activity (Table 2). In both markets, high counterparty-risk lenders tend to lend to high counterparty-risk borrowers (first row, columns (a) to (f)), and, in the unsecured market, high counterparty-risk borrowers tend to borrow from high-collateral lenders (third row, columns (a) and (b)). The causes of these correlations are not entirely clear – Jaremski and Wheelock (2020) argue that there is still much to understand about interbank network formation, and Brassil and Nodari (2018) show that shocks can have long-lasting impacts on interbank network structures. Nonetheless, the patterns demonstrate the importance of controlling for the behaviour of counterparties. In regression specifications (1) and (2), we achieve this with counterparty*day fixed effects.
| Market: | Unsecured | Repo | Total | |||||
|---|---|---|---|---|---|---|---|---|
| Regressand: | LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | ||
| (a) | (b) | (c) | (d) | (e) | (f) | |||
| CPRiskb * CPRiskl | 0.065 (0.039) |
0.014*** (0.005) |
0.042 (0.044) |
0.031 (0.018) |
0.119** (0.048) |
0.033*** (0.010) |
||
| Collateralb * Collaterall | 0.078 (0.048) |
0.017 (0.011) |
−0.010 (0.100) |
−0.009 (0.020) |
0.092 (0.075) |
0.015 (0.015) |
||
| CPRiskb * Collaterall | 0.080*** (0.018) |
0.016*** (0.003) |
0.056 (0.092) |
0.023 (0.020) |
0.052 (0.067) |
0.010 (0.013) |
||
| Collateralb * CPRiskl | −0.050 (0.058) |
−0.010 (0.010) |
0.001 (0.064) |
0.004 (0.019) |
−0.018 (0.069) |
0.000 (0.014) |
||
| Lower-level interactions | Yes | |||||||
| Fixed effects | Borrower and Lender and Day | |||||||
| Observations | 5,340 | 5,340 | 2,840 | 2,840 | 7,000 | 7,000 | ||
| R-squared | 0.095 | 0.074 | 0.168 | 0.118 | 0.138 | 0.120 | ||
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively. This table contains results from regressing loans outstanding, in log millions plus one ( LoanValueslbd ), and an indicator variable for whether LoanValueslbd is positive ( Participationlbd ), on interactions between borrower and lender characteristics. Columns (a) and (b) use the unsecured sample, columns (c) and (d) use the repo sample, and columns (e) and (f) treat the two markets as a single combined market. The pre-interacted explanatory variables are each standardised to zero mean and unit variance. The full variable definitions are in Section 2.4. Standard errors are clustered at the borrower and lender and day levels. | ||||||||
The borrower results from specification (1) are in Table 3. In the unsecured market, market stress causes a relative decline in riskier banks' borrowing, irrespective of how much collateral they hold (columns (a) to (d)). Afonso et al (2011) find a similar negative interaction between the Lehman Brothers default and counterparty risk on unsecured borrowing activity.[11] To interpret the effect size implied by the −0.247 coefficient in column (b), consider a representative scenario, with banks A and B that each have $150 million outstanding unsecured loans per engaged lender:
bank A has mean; CPRiskb and
bank B has CPRiskb one standard deviation above the mean.
The riskier bank B is estimated to reduce borrowing (from each lender) by $33 million more than bank A. This is illustrated in Figure 5 by the light bars. The effect of counterparty risk on borrowers' participation – that is, number of lender counterparties – is also statistically significant (columns (c) and (d)), but not large. Consider again the scenario above. If both banks borrow unsecured from 10 lenders throughout the sample (see Table 1, panel C), the coefficient of −0.049 implies that borrower B has 0.5 fewer counterparties on an average day after the Lehman Brothers default, relative to borrower A. The effect of counterparty risk is therefore mostly in the intensive margin – banks reduced the quantities lent to risky borrowers, rather than cutting lending altogether.
In the repo market, borrowers' collateral holdings are stronger determinants of reactions to stress than their counterparty risk (Table 3, columns (e) to (h)). Borrower counterparty risk does not have a significant effect for a borrower with mean collateral holdings. In contrast, collateral holdings determine borrowing directly as well as through the interaction with counterparty risk (columns (f) and (h)). To interpret the coefficient sizes, consider another representative scenario, with banks A, B and C that each have $80 million repo loans outstanding per engaged lender:
bank A has mean CPRiskb and mean Collateralb;
bank B has mean CPRiskb and Collateralb one standard deviation above the mean;
bank C has CPRiskb one standard deviation above the mean and Collateralb one standard deviation above the mean.
In this scenario, the coefficients in column (f) estimate that bank B increases borrowing by $25 million per lender more than the lower collateral bank A. However, for bank C, whose CPRiskb is also one standard deviation above the mean, the effects of high counterparty risk and high collateral holdings compound, and its borrowing is estimated to increase by $70 million more than bank A. Alternatively, if bank C's CPRiskb was one standard deviation below the mean, the effects of high collateral and low counterparty risk offset each other, and the change in borrowing is estimated to be roughly equal to bank A. These estimated effects are illustrated in Figure 5 by the dark bars.
| Market: | Unsecured | Repo | Total | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regressand: |
LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | |||||||||||
| (a) | (b) | (c) | (d) | (e) | (f) | (g) | (h) | (i) | (j) | (k) | (l) | ||||||
| LBd * | |||||||||||||||||
| CPRiskb | −0.166*** (0.053) |
−0.247** (0.090) |
−0.038*** (0.009) |
−0.049** (0.019) |
−0.171 (0.134) |
−0.019 (0.117) |
−0.026 (0.045) |
0.023 (0.032) |
−0.178* (0.085) |
−0.141 (0.103) |
−0.033 (0.020) |
−0.013 (0.024) |
|||||
| Collateralb | 0.108 (0.087) |
0.019 (0.108) |
0.013 (0.018) |
0.001 (0.023) |
0.053 (0.095) |
0.267*** (0.082) |
0.015 (0.027) |
0.084*** (0.020) |
0.109 (0.071) |
0.149 (0.091) |
0.021 (0.016) |
0.043* (0.024) |
|||||
| CPRiskb * Collateralb | −0.151 (0.127) |
−0.021 (0.030) |
0.358*** (0.097) |
0.117*** (0.014) |
0.073 (0.122) |
0.039 (0.029) |
|||||||||||
| Fixed effects | Borrower and Lender * Day | ||||||||||||||||
| Observations | 5,780 | 5,780 | 5,780 | 5,780 | 3,020 | 3,020 | 3,020 | 3,020 | 7,660 | 7,660 | 7,660 | 7,660 | |||||
| R-squared | 0.227 | 0.227 | 0.219 | 0.219 | 0.248 | 0.251 | 0.218 | 0.222 | 0.224 | 0.224 | 0.215 | 0.216 | |||||
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively. This table reports estimates from lender-borrower-day level regressions on sub-samples containing a particular interbank market (i.e. specification (1)). We regress loans outstanding, in log millions plus one ( LoanValueslbd ), and an indicator variable for whether LoanValueslbd is positive ( Participationlbd ), on interactions between borrower characteristics and market stress. Columns (a) to (d) use the unsecured sample, columns (e) to (h) use the repo sample, and columns (i) to (l) treat the two markets as a single combined market. The pre-interacted explanatory variables are borrowers' counterparty risk ( CPRiskb ), borrowers' pre-sample high-quality collateral holdings ( Collateralb ) and an indicator variable equal to one after the Lehman Brothers default ( LBd ). CPRiskb and Collateralb are standardised to zero mean and unit variance. The full variable definitions are in Section 2.4. Standard errors are clustered at the borrower and lender and day levels. | |||||||||||||||||
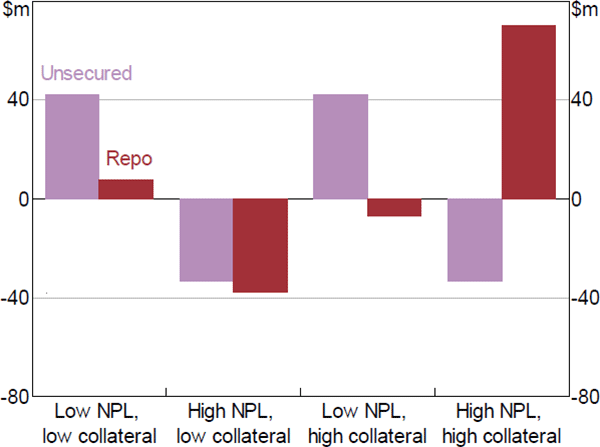
Krishanmurthy et al (2014) find that after the Lehman Brothers default, dealers' repo borrowing from money market funds becomes negatively correlated to how much of the dealers' borrowing is against lower-quality collateral. They conclude that this was driven by the collateral that these dealers held. Our formal results show that collateral holdings are indeed a significant determinant of reactions to stress, in support of their conclusion. di Filippo et al (2018) find a positive effect of counterparty risk on repo borrowing, in a specification without collateral holdings. We do not find a similar positive effect, but show that counterparty risk increases the positive effect of collateral holdings on repo borrowing.
The estimated effect of collateral holdings on repo borrowing is through both the intensive and extensive margins. Consider the same scenarios discussed two paragraphs earlier, with the three banks each borrowing repo from ten different lenders throughout the sample (see Table 1, panel C). Bank C is estimated to borrow from two additional lenders after the shock, relative to bank A.
The result that extensive margin responses are more pronounced in the repo market than the unsecured market is consistent with theory that collateral reduces information frictions. If the collateral is high enough quality, banks can trade with additional counterparties without first seeking information about expected default losses (Dang et al 2015). Relative to unsecured lending, collateralisation should therefore facilitate faster changes in the network of lending relationships. In line with this interpretation, the number of active counterparty pairs in the repo market picks up by 16 per cent in our sample, from a mean of 50 before the Lehman Brothers default to 58 afterward, while in the unsecured market, the corresponding means change by half that amount, from 53 to 49.[12]
When repo and unsecured borrowing are combined into a single measure of interbank borrowing, we do not find a robust significant net effect of counterparty risk (columns (i) to (l) of Table 3). However, collateral holdings are a significant determinant of cross-sectional differences in extensive-margin reactions, driven by the repo market behaviour discussed above.
4.2 Borrowers' Substitution between the Repo and Unsecured Markets
Specification (2) formally tests whether borrowers' reactions to stress differ across the collateralised and uncollateralised markets. We reject the hypothesis that collateralisation has no effect on interbank market functioning (Table 4), consistent with Section 4.1. Riskier borrowers shift towards the repo market. For riskier borrowers with large collateral holdings, the shift is significantly larger. Note also that aggregate repo borrowing is growing while unsecured borrowing is relatively flat (Figure 3), which suggests that substitutions into the repo market would have likely more than offset any decline in unsecured borrowing.
| Regressand: | LoanValueslbdm | Participationlbdm | |||
|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | ||
| 1s * LBd * | |||||
| CPRiskb | 0.091*** (0.020) |
0.166*** (0.032) |
0.026** (0.009) |
0.047*** (0.012) |
|
| Collateralb | −0.023 (0.057) |
0.061 (0.070) |
0.005 (0.016) |
0.029* (0.015) |
|
| CPRiskb * Collateralb | 0.151** (0.061) |
0.043*** (0.015) |
|||
| Lower-level interactions | Yes | ||||
| Fixed effects | Borrower * Lender * Day | ||||
| Observations | 15,600 | 15,600 | 15,600 | 15,600 | |
| R-squared | 0.531 | 0.533 | 0.504 | 0.505 | |
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively. This table reports estimates from lender-borrower-day-market level regressions on a sample containing the unsecured and repo markets (i.e. specification (2)). We regress loans outstanding, in log millions plus one ( LoanValueslbdm ), and an indicator variable for whether LoanValueslbdm is positive ( Participationlbdm ), on interactions between borrower characteristics, market stress and an indicator variable for whether the observation is on the repo market. The pre-interacted explanatory variables are borrowers' counterparty risk ( CPRiskb ), borrowers' pre-sample high-quality collateral holdings ( Collateralb ), an indicator variable equal to one after the Lehman Brothers default ( LBd ), and the repo-market indicator ( 1s ). CPRiskb and Collateralb are standardised to zero mean and unit variance. The full variable definitions are in Section 2.4. Standard errors are clustered at the borrower and lender and day levels. | |||||
To analyse the robustness of this key result to model specification and omitted variables, we re-estimate specification (2) for a wide range of fixed effects combinations, focusing on the coefficient of interest on 1s × LBd × CPRiskb × Collateralb. Oster (2019) demonstrates that as controls are added to a regression, the ratio of the change in coefficients to the change in R-squared is indicative of the degree of omitted variable bias remaining. As we add fixed effects, the coefficient estimates are stable (slightly increasing), while the explained variance ranges from 3 per cent to 70 per cent (Table 5). This is strong evidence that our results are not being overstated by omitted variable bias. The coefficient stability also addresses potential concerns about fixed effects narrowing the variance of interest to unrepresentative sub-samples (Miller, Shenhav and Grosz 2019).
These results also add support to our choice of specification (2). The marked change in R-squared demonstrates that unobservables contribute substantially to interbank activity, which appears common in analysis of interbank lending quantities (e.g. Cocco et al 2009; Afonso et al 2011; di Filippo et al 2018), and is consistent with theory that random liquidity shocks are the main driver of activity (e.g. Allen, Carletti and Gale 2009; Freixas, Martin and Skeie 2011). Fixed effects saturation is therefore appropriate. Moreover, these results show that the most influential level of fixed effects is borrower * lender * day (see columns (i) and (j), Table 5), supporting our choice for specification (2).[13]
| (a) | (b) | (c) | (d) | (e) | (f) | (g) | (h) | (i) | (j) | (k) | (l) | (m) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regressand: LoanValueslbdm | |||||||||||||
| 1s * LBd * CPRiskb * Collateralb | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.151 | 0.172 |
| Statistical significance | ** | ** | ** | ** | ** | ** | ** | ** | ** | ** | ** | * | *** |
| R-squared | 0.023 | 0.044 | 0.045 | 0.088 | 0.079 | 0.112 | 0.192 | 0.122 | 0.168 | 0.533 | 0.533 | 0.668 | 0.706 |
| Regressand: Participationlbdm | |||||||||||||
| 1s * LBd * CPRiskb * Collateralb | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.043 | 0.047 |
| Statistical significance | ** | ** | ** | ** | *** | ** | ** | *** | *** | *** | *** | ** | *** |
| R-squared | 0.025 | 0.044 | 0.045 | 0.080 | 0.078 | 0.112 | 0.158 | 0.113 | 0.163 | 0.505 | 0.505 | 0.660 | 0.702 |
| Lower-level interactions | yes | yes | yes | yes | yes | yes | yes | yes | yes | yes | yes | yes | yes |
| Fixed effects | |||||||||||||
| Borrower | no | yes | yes | yes | . | no | . | . | . | . | . | . | . |
| Day | no | no | yes | yes | . | . | no | . | . | . | . | . | . |
| Lender | no | no | no | yes | no | . | . | yes | . | . | . | . | . |
| Secured | no | no | no | no | no | no | no | no | no | no | yes | . | . |
| Borrower * Day | no | no | no | no | yes | no | no | yes | yes | . | . | . | . |
| Lender * Day | no | no | no | no | no | yes | no | no | yes | . | . | . | . |
| Borrower * Lender | no | no | no | no | no | no | yes | no | no | . | . | . | . |
| Borrower * Lender * Day | no | no | no | no | no | no | no | no | no | yes | yes | yes | yes |
| Secured * Borrower * Lender | no | no | no | no | no | no | no | no | no | no | no | yes | yes |
| Secured * Lender * Day | no | no | no | no | no | no | no | no | no | no | no | no | yes |
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively. This table reports the primary coefficient of interest from specification (2), i.e. the interaction between borrower counterparty risk, borrower collateral, market stress and the repo market indicator, across varying levels of fixed effects. The dependent variables are loans outstanding, in log millions plus one ( LoanValueslbdm ), and an indicator variable for whether LoanValueslbdm is positive ( Participationlbdm ). The pre-interacted explanatory variables are borrowers' counterparty risk ( CPRiskb ), borrowers' pre-sample high-quality collateral holdings ( Collateralb ), an indicator variable equal to one after the Lehman Brothers default ( LBd ), and the repo market indicator ( 1s ). CPRiskb and Collateralb are standardised to zero mean and unit variance. The full variable definitions are in Section 2.4. Standard errors are clustered at the borrower and lender and day levels. | |||||||||||||
4.3 Heterogeneity across Lenders
This section explores how responses to stress vary across lender characteristics. A reduction in unsecured lending could be consistent with banks building up liquidity buffers to protect against future illiquidity (e.g. Acharya and Skeie 2011; Gale and Yorulmazer 2013). Two potential manifestations in our sample are the following. First, banks with more solvency risk could reduce unsecured lending due to fear of funding runs. Second, banks could reduce unsecured lending because they hold less collateral, and therefore have less capacity to handle a future shock. In a high-quality collateral repo market, however, it is a priori unclear how liquidity hoarding would relate to lending activity. Each lender's reduction in cash is offset by an increase in liquid assets, with little net effect on the bank's access to liquidity.
We explore lending motives by applying specification (1) to lender characteristics, and also by exploring how lenders' characteristics determine their repo borrowing from the RBA. RBA repos are informative about interbank lending because banks sometimes fund their interbank lending by borrowing from the RBA. RBA repos are less relevant for the borrower analysis in Section 4.1 because they are not a direct substitute for interbank borrowing (see Section 2.1).
There is little supporting evidence for liquidity hoarding in the unsecured market (Table 6, columns (a) to (d)). The coefficients on CPRiskl are small and not significant, and the coefficients on Collaterall are negative. Similarly, Afonso et al (2011) conclude that there is little evidence of liquidity hoarding in the US unsecured market during the same period.
The results in Table 6 also suggest a relative pick-up in repo lending by: (i) safer banks with low collateral holdings, and (ii) riskier banks with high collateral holdings (i.e. the significant coefficients in columns (f) and (h)). It is likely that type (i) banks are lending to acquire liquid asset holdings, potentially funded by the pick-up in unsecured borrowing documented in Section 4.1, which would imply an overall net inflow of liquidity. Comparing these results with banks' repo borrowing from the RBA, in open market operations (OMO), sheds some light on the pick-up in repo lending by type (ii) banks. Type (ii) banks increase borrowing from the RBA against AGS and semis (column (n)), and Section 4.1 shows that they also increase interbank repo borrowing. With both sources of incoming funds, it is plausible that the pick-up in lending is to signal their strong liquid asset position to other banks that might otherwise treat them as risky. Afonso et al (2011) speculate similar motives for unexplained patterns in unsecured lending behaviour.
| Market: | Unsecured | Repo | Total | AGS/semis collateral | Private collateral | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Regressand: |
LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | OMOld | |||||||||||||||
| (a) | (b) | (c) | (d) | (e) | (f) | (g) | (h) | (i) | (j) | (k) | (l) | (m) | (n) | (o) | (p) | |||||||
| LBd * | ||||||||||||||||||||||
| CPRiskl | −0.065 (0.102) |
−0.023 (0.116) |
−0.012 (0.023) |
−0.006 (0.025) |
−0.034 (0.125) |
0.106 (0.112) |
−0.014 (0.039) |
0.017 (0.039) |
−0.055 (0.079) |
0.039 (0.088) |
−0.010 (0.020) |
0.008 (0.022) |
−0.072 (0.577) |
0.435 (0.362) |
1.054** (0.391) |
1.009* (0.524) |
||||||
| Collaterall | −0.297** (0.126) |
−0.189 (0.123) |
−0.054** (0.024) |
−0.040 (0.027) |
−0.014 (0.153) |
0.409 (0.276) |
−0.011 (0.057) |
0.082 (0.083) |
−0.135 (0.131) |
0.094 (0.096) |
−0.017 (0.035) |
0.027 (0.028) |
−0.406 (0.549) |
1.031* (0.493) |
1.067* (0.538) |
0.938 (1.018) |
||||||
| CPRiskl * Collaterall | 0.162 (0.153) |
0.022 (0.030) |
0.613** (0.279) |
0.136* (0.074) |
0.344* (0.172) |
0.066 (0.041) |
2.319*** (0.619) |
−0.207 (1.026) |
||||||||||||||
| Fixed effects | Lender and Borrower * Day | Lender and Day | ||||||||||||||||||||
| Observations | 5,360 | 5,360 | 5,360 | 5,360 | 3,060 | 3,060 | 3,060 | 3,060 | 7,240 | 7,240 | 7,240 | 7,240 | 380 | 380 | 380 | 380 | ||||||
| R-squared | 0.229 | 0.230 | 0.217 | 0.218 | 0.240 | 0.246 | 0.205 | 0.210 | 0.218 | 0.219 | 0.204 | 0.206 | 0.611 | 0.646 | 0.687 | 0.687 | ||||||
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively. Columns (a) to (l) contain estimates from regressing loans outstanding, in log millions plus one ( LoanValueslbd ), and an indicator variable for whether LoanValueslbd is positive ( Participationlbd ), on interactions between lender characteristics and market stress. Columns (a) to (d) use the unsecured sample, columns (e) to (h) use the repo sample, and columns (i) to (l) treat the two markets as a single combined market. The pre-interacted explanatory variables are banks' counterparty risk ( CPRiskl ), banks' pre-sample high-quality collateral holdings ( Collaterall ) and an indicator variable equal to one after the Lehman Brothers default ( LBd ). CPRiskl and Collaterall are standardised to zero mean and unit variance. The full variable definitions are in the Section 2.4. Standard errors are clustered at the borrower and lender and day levels. Columns (m) to (p) report regressions using a different dependent variable. The dependent variable is, at the lender-day level, each lender's daily outstanding borrowing of RBA repos, in log AUD millions ( OMOld ), against two separate collateral categories: AGS and semis combined (i.e. government debt securities); and private, which includes everything else. The OMO data excludes RBA repos against discount securities, which, unlike for interbank repos, may have been a non-negligible portion of total RBA repos in the sample (e.g. Kearns 2009). Changes in outstanding RBA repo balances are inferred from transactions between banks and the RBA's OMO account in the Austraclear data. The starting values of these repo positions is pinned down by assuming that the minimum sample value of each bank's outstanding position is AUD 1 million. Standard errors are clustered at the lender and day levels. | ||||||||||||||||||||||
4.4 The Role of Collateral Type in the Repo Market
This section compares how the repo market segments against different collateral types reacted to the market stress surrounding the Lehman Brothers default. Most collateral in the Australian repo market is issued by either the national or state governments (AGS and semis, respectively). Both categories are widely considered to be low risk and are included in the regulatory definition of high-quality liquid assets. Notwithstanding, AGS have higher average credit ratings and are more liquid than semis, related to the fact that the national government is a higher authority than the state governments.
Differences in market behaviour around the Lehman Brothers default are clear from plots of the market sizes and interest rates (Figure 6). The aggregate repo market expansion discussed at the start of Section 4 comprises repos against semis, while the total value of AGS repos remains flat. At the same time, AGS repo spreads (to the cash rate) fall heavily while spreads on repos against semis are relatively stable. Together, these patterns indicate a scarcity of AGS alongside a demand for funding that was satisfied in the semis repo market. Indeed, at the time, the Australian Government had very little debt outstanding, and the face value of semis on issue was greater than that of AGS.
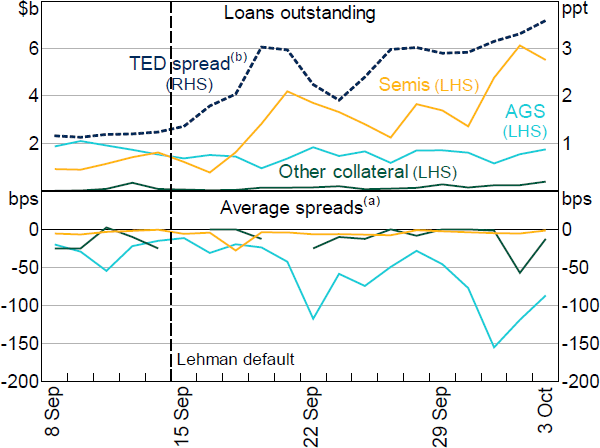
Notes:
(a) Spreads are to the cash rate, measured for loans initiated that day; to construct market-wide average, counterparty pairs are weighted equally and loans within a pair are value weighted
(b) Lagged one day to account for time zones
Sources: ASX; Authors' calculations; Federal Reserve Bank of St. Louis; RBA
The heavy decline in AGS repo rates likely included special repos. Special repos are repos driven by demand for the specific securities received, with the cash side acting as collateral for the loan of securities. They can be difficult to distinguish from other repos (i.e. general collateral, or ‘GC’, repos), both conceptually and observationally in our data.[14] Demand for particular securities can push down interest rates on special repos, particularly when those securities are scarce. Nevertheless, rates on GC AGS repos would also be expected to fall when there is a pick-up in general demand for holding liquid assets. Indeed, Bartolini et al (2011) show that during periods of (non-crisis) heightened liquidity demand in the United States, noticeable spreads opened up between GC Treasury repos and GC agency repos, driven by declining GC Treasury rates. Our data indicate that the decline in AGS repo rates was at least partly driven by GC repos: the largest declines involved AGS ISINs that were relatively frequently used as collateral in the second half of the sample.
To examine the bank-level behaviour within the aggregate volumes, we estimate specification (1) on each of the AGS and semis repo markets, also separating the two types of banks' collateral holdings (i.e. Collateralb is replaced by AGSb and Semisb ). The results show that the risk–collateral interaction reported in Section 4.1 is significant for both collateral types (in their respective markets), but that riskier banks with large holdings of both types of collateral tend to borrow against AGS rather than semis (Table 7). That is, the counterparty risk–semis interaction coefficients increase from around zero only when AGS holdings are controlled for (columns (c), (d), (g) and (h)), while the counterparty risk–AGS interaction coefficients are uniformly significant with and without semis controls (columns (a), (b), (e) and (f)). Similarly, high counterparty-risk borrowers with large AGS holdings shift out of the semis market (columns (g) and (h)), but there is no such shift in the opposite direction (columns (e) and (f)).
The tendency for high counterparty-risk banks to increase borrowing against AGS rather than semis has plausible explanations on both the lender and borrower sides. Lenders may have been less willing to lend to high counterparty-risk borrowers against semis, given that AGS are higher quality. Alternatively, borrowers with high counterparty risk, substituting from the unsecured market (Section 4.2), may have been taking advantage of low interest rates in the AGS market (Figure 6, bottom panel).
To test these potential explanations we re-estimate the regressions in Table 7 with repo rates as a dependent variable. The results (in Appendix B) show that borrowers that substituted into the AGS market were receiving good terms – in the AGS market, the counterparty risk–AGS interaction coefficients are negative and significant at 90 per cent (Table B1). This runs against the supply-side explanation that riskier borrowers that had both types of collateral were pushed to borrow against AGS. Rather, it suggests that riskier borrowers chose to borrow against AGS. That is, the heightened demand for liquid assets eased funding conditions for riskier borrowers, by lowering borrowing rates.
Aside from this, the repo rate regressions mostly produce null results. Overall, counterparty risk does not appear to be a strong determinant of repo rates, consistent with findings of Krishnamurthy et al (2014), and with findings for unsecured loans (discussed in Section 2.1).
| Market: | AGS | Semis | AGS | Semis | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Regressand: |
LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | LoanValueslbd | Participationlbd | |||
| (a) | (b) | (c) | (d) | (e) | (f) | (g) | (h) | ||||
| LBd * | |||||||||||
| CPRiskb | 0.254* (0.119) |
0.055 (0.040) |
−0.247** (0.093) |
−0.010 (0.023) |
0.295** (0.133) |
0.066 (0.043) |
−0.276* (0.134) |
−0.015 (0.017) |
|||
| AGSb | 0.377*** (0.099) |
0.080** (0.031) |
0.326*** (0.104) |
0.054 (0.037) |
−0.298*** (0.058) |
−0.069*** (0.007) |
|||||
| CPRiskb * AGSb | 1.084*** (0.189) |
0.220*** (0.058) |
1.044*** (0.199) |
0.187*** (0.057) |
−0.755** (0.256) |
−0.169*** (0.042) |
|||||
| Semisb | 0.019 (0.089) |
0.033 (0.026) |
0.135** (0.048) |
0.046 (0.038) |
0.321*** (0.106) |
0.103** (0.037) |
|||||
| CPRiskb * Semisb | −0.018 (0.053) |
0.061*** (0.017) |
0.045* (0.025) |
0.041 (0.037) |
0.401*** (0.060) |
0.157*** (0.023) |
|||||
| Fixed effects | Borrower and Lender * Day | ||||||||||
| Observations | 2,660 | 2,660 | 1,640 | 1,640 | 2,660 | 2,660 | 1,640 | 1,640 | |||
| R-squared | 0.273 | 0.242 | 0.264 | 0.236 | 0.274 | 0.242 | 0.269 | 0.240 | |||
| Notes: *, ** and *** denote significance at the 10, 5 and 1 per cent levels, respectively. This table reports estimates from lender-borrower-day level regressions separating the repo market by collateral type (using specification (1)). We regress loans outstanding, in log millions plus one ( LoanValueslbd ), and an indicator variable for whether LoanValueslbd is positive ( Participationlbd ), on interactions between borrower characteristics and market stress. Columns (a), (b), (e) and (f) examine repos collateralised by AGS and columns (c), (d), (g) and (h) examine repos collateralised by semis. The pre-interacted explanatory variables are borrowers' counterparty risk ( CPRiskb ), borrowers' pre-sample AGS holdings ( AGSb ), borrowers' pre-sample semis holdings ( Semisb ) and an indicator variable equal to one after the Lehman Brothers default ( LBd ). CPRiskb , AGSb and Semisb are standardised to zero mean and unit variance. The full variable definitions are in Section 2.4. Standard errors are clustered at the borrower and lender and day levels. | |||||||||||
Footnotes
Behind these aggregates, the repo market expansion mostly reflects borrowing by a subset of entities, although repo activity by other entities also picks up by a similar proportion. Aside from the aggregate plots of outstanding loans, all the analysis in this paper maintains representativeness across entities. [8]
The subtracted means are bank and market specific, across days. [9]
Most of the fitted lines become steeper when outliers are removed. [10]
They find this result for the large banks in their sample. Most of our sample comprises the largest Australian banks and prominent international banks, so it is more comparable to their large-bank sub-sample than their small-bank sub-sample. [11]
Pairs of banks require a bilateral Global Master Repurchase Agreement (GMRA) in place before they can engage in repo with each other. The extensive margin change that we find is most likely between counterparty pairs that have pre-existing GMRAs, but that prior to the shock do not regularly engage each other, and therefore may not have up-to-date credit risk beliefs about each other. [12]
The unreported specification with borrow-lender, borrower-day and lender-day fixed effects explains 24 to 27 per cent of the variation in the dependent variables. [13]
Australian haircut data demonstrate the conceptual difficulty in distinguishing special and GC repos. In the United States, the amount of cash in a special repo (also called a securities loan) typically exceeds the value of the securities (Foley-Fisher, Narajabad and Verani 2016). This reflects that the loan is driven by demand from the securities receiver, so the securities receiver overcollateralises the securities provider (whereas in a GC repo the cash receiver overcollateralises the cash provider). To an onlooker who thought it was a GC repo, this would appear as a negative haircut. Garvin (2018) shows that haircuts on Australian repos tend to be continuously and randomly distributed around zero, with no clear gap between positive and negative haircuts. [14]