RDP 2019-08: The Well-meaning Economist 3. Switching Can Transform Conclusions
September 2019
- Download the Paper 2,045KB
3.1 Examples in Trade
Anderson (2011) writes that the so-called gravity model has ‘long been one of the most successful empirical models in economics’ (p 133). Starting with Tinbergen (1962), it has been the subject of a large empirical literature on the determinants of trade flows in particular. A stylised form of the set-up most commonly used today is
where: Tij is trade from country i to country j; Si is output size of country i; Dij denotes ‘distance’, covering sources of trade resistance like trade policies and physical distance; the various are parameters of interest to the researcher (mostly elasticities); and is a random error term, which has properties that I deliberately leave undefined (for now).
The literature contains many methods for estimating the elasticities and, in the latest Handbook of International Economics, Head and Mayer (2014) write that choosing among them is a ‘frontier’ issue. But it turns out that in many cases the choice just amounts to deciding which quasilinear mean to target. Although not deliberately, the different estimation methods target at least four different types of quasilinear mean:
-
Tinbergen (1962) log-transformed both sides of Equation (4) and applied OLS. Two recent papers, Petersen (2017) and Mitnik and Grusky (2017), show that the method effectively targets elasticities for the geometric mean of trade. Postponing a more complete econometric discussion for Section 5.4, the idea is that the method is consistent and unbiased for the elasticity parameters that are defined by the error condition
5in which case
6The left-hand side of Equation (6) defines a geometric mean.
- Another estimation method takes the same route, except that it swaps the log transformation of the dependent trade variable with a GSL transformation. Researchers have used this approach when working with datasets containing zero values for some trade flows, which then have undefined logarithms.[4] A contribution of this paper is to show that the effective targets are elasticities for GSL means of trade. The logic will be similar to the geometric case, with an added complication.
- Another method takes the same route again, except for IHS-transforming the dependent trade variable. It too is a solution for zero values. It was popularised by Burbidge, Magee and Robb (1988) and is more common outside of trade.[5] A contribution of this paper is to show that the effective targets are elasticities for IHS means.
- A final group of methods includes Poisson pseudo-maximum likelihood (PPML), gamma pseudo-maximum likelihood (GPML) and nonlinear least squares (NLS). An influential paper by Santos Silva and Tenreyro (2006) introduced these methods to the trade literature. Starting with an explicit assumption that researchers are aiming to learn about a conditional arithmetic mean – earlier papers are unclear on this – they argue that the other methods are inconsistent for the target elasticities regardless of whether there are zeros.
It stands to reason, then, that we can view the inconsistencies raised in Santos Silva and Tenreyro (2006) as actually being the footprint of targeting different quasilinear means. Hence their paper is informative for the importance of choosing means carefully.
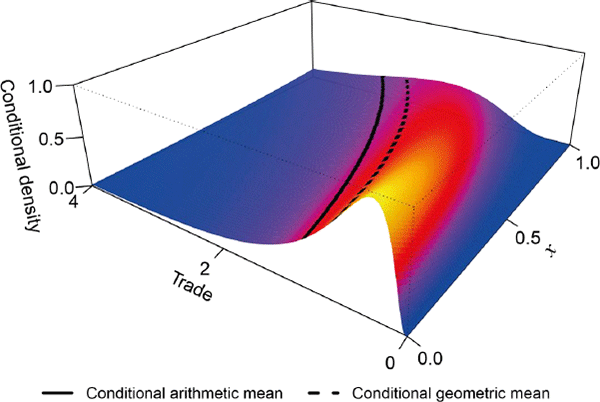
To argue their case, Santos Silva and Tenreyro draw partly on a set of simulations, which use log normal distributions so there are no zeros to worry about. Inspecting their preferred data-generating process, it is clear that the arithmetic and geometric means trace out two distinct functions (Figure 2; I focus on these two means because they are far apart). As is the case for all non-degenerate distributions, Jensen's inequality implies that the geometric mean is smaller than the arithmetic mean for every value of the independent variable.
Since the data-generating process is orderly, without unruly changes in variance and higher moments, the slopes of the arithmetic and geometric means look similar. Still, the elasticity of trade with respect to x is everywhere larger for the geometric mean, owing to base effects. Unsurprisingly then, Santos Silva and Tenreyro find that the Tinbergen method overstates their target elasticity in the simulation. Their other data-generating processes produce wider differences.
Santos Silva and Tenreyro (2006) also conduct an empirical comparison of methods, on a cross-section of 136 countries in 1990. They use a ‘traditional’ set of explanatory variables and a set from Anderson and van Wincoop (2003, AVW), which includes controls for so-called multilateral resistance. To abstract from the issue of zeros, they use a trunwcated version of the sample to compare the Tinbergen and PPML estimation methods on both sets of explanatory variables. Table 1 displays the effect sizes that differ most. It shows that the PPML estimates imply much smaller effects (in magnitude) of physical distance and colonial ties than the Tinbergen estimates. The estimated impacts of FTAs are different too, particularly in the traditional model.[6] The sheer size of the differences suggests that the true data-generating process is far less orderly than the one in Figure 2.
Then on the full sample of 18,360 observations, Santos Silva and Tenreyro (2006) estimate the gravity parameters with NLS, PPML, and the method based around a GSL transformation. Again, several of the differences are stark, particularly between the methods that target different quasilinear means (Table 2). Methods that target arithmetic means (NLS and PPML) still estimate noticeably lower (in magnitude) effects of distance and colonial ties. The differences might reflect a degree of sampling error, but Fally (2015) makes similar comparisons on more recent data, obtaining comparable results.
| Traditional | AVW version | ||||
|---|---|---|---|---|---|
| OLS ln(Tij) |
PPML Tij |
OLS ln(Tij) |
PPML Tij |
||
| 10% more physical distance | −11.7** (0.3) |
−7.8** (0.6) |
−13.5** (0.3) |
−7.7** (0.4) |
|
| Having colonial ties | 39.7** (7.0) |
1.9 (15.0) |
66.6** (7.0) |
3.8 (13.4) |
|
| Exporter is landlocked | −6.2 (6.2) |
−87.3** (15.7) |
|||
| 10% more importer remoteness(a) | −2.1* (0.9) |
5.5** (1.2) |
|||
| Having an FTA together | 49.1** (9.7) |
17.9* (9.0) |
31.0** (9.8) |
37.4** (7.6) |
|
| Sharing a border | 31.4* (12.7) |
20.2 (10.5) |
17.4 (13.0) |
35.2** (9.0) |
|
| Effective observations | 9,613 | 9,613 | 9,613 | 9,613 | |
|
Notes: ** and * denote statistical significance at the 5 and 10 per cent levels, respectively; figures in parentheses are standard errors Source: Santos Silva and Tenreyro (2006) |
|||||
| Traditional | AVW version | ||||
|---|---|---|---|---|---|
| OLS ln(Tij + 1) |
PPML Tij |
OLS ln(Tij + 1) |
PPML Tij |
||
| 10% more physical distance | −11.5** (0.3) |
−7.8** (0.6) |
−13.3** (0.4) |
−7.5** (0.4) |
|
| Having colonial ties | 39.2** (7.0) |
2.4 (15.0) |
69.3** (6.7) |
7.9 (13.4) |
|
| Exporter is landlocked | 10.6 (5.4) |
−86.4** (15.7) |
|||
| 10% more importer remoteness(a) | −1.1 (0.9) |
5.6** (1.2) |
|||
| Having an FTA together | 128.9** (12.4) |
18.1* (8.8) |
17.4 (13.8) |
37.6** (7.7) |
|
| Sharing a border | −24.1 (20.1) |
19.3 (10.4) |
−39.9* (18.9) |
37.0** (9.1) |
|
| Effective observations | 18,360 | 18,360 | 18,360 | 18,360 | |
|
Notes: ** and * denote statistical significance at the 5 and 10 per cent levels, respectively; figures in parentheses are standard errors Source: Santos Silva and Tenreyro (2006) |
|||||
3.2 Examples in Wages
Others have made similar comparisons in applications outside of trade, partly reflecting the widespread influence of the Santos Silva and Tenreyro (2006) paper. Petersen (2017), for example, studies the relationship between employment status (self-employed versus contract employed) and annual earnings, using a sample of 12,800 native-born black men in California. With a simple multivariate set-up, he shows that GPML, PPML, and NLS estimate a positive premium for the self-employed that is between 7 and 15 per cent and statistically significant. These are all estimated differences in arithmetic means. Using the Tinbergen method, he estimates a premium for the self-employed that is minus 16 per cent and statistically significant. This is an estimated difference in geometric means, which he emphasises. The contrasting narratives are consistent with self-employed people having much wider variation in incomes than contract-employed people, because the geometric mean penalises dispersion.[7]
Gabaix and Landier (2008) study the determinants of CEO earnings, using samples of between 3,000 and 8,000 compensation packages for CEOs in the United States. Though they do not show the comparison, they report that PPML and the Tinbergen approach both produce ‘extremely close results’ (p 70). So here the choice between targeting arithmetic and geometric means looks inconsequential.
Bellemare and Wichman (forthcoming) estimate the effect on annual earnings of a worker support program. Using data from LaLonde (1986), their sample consists of 445 disadvantaged US workers, to which the program was randomly assigned. Using the method that targets the IHS mean, the program is estimated to increase annual earnings by 148 per cent.[8] Using the method that targets the GSL mean, the estimate is 164 per cent. The contrast is material but not stark.
3.3 An Example in Hospital Costs
Manning, Basu and Mullahy (2005) study the effect of introducing ‘hospitalists’ on the cost of patient care, with a sample that covers 6,500 patient cases at the University of Chicago Medical Center.[9] Using both the GPML and Tinbergen methods, the hospitalists had an estimated impact that was statistically and economically insignificant. Here the choice between targeting geometric and arithmetic means looks inconsequential again.
Footnotes
A sophisticated version is Eaton and Tamura (1994). They treat as a threshold value under which trade is censored as a zero, and use maximum likelihood estimation. [4]
Johnson (1949) introduced the IHS transformation to the statistics literature. Recent econometric applications include research on household finances (Clemens and Tiongson 2017), deforestation (Jayachandran et al 2017), entrepreneurship (McKenzie 2017), knowledge spillovers (Bahar and Rapoport 2018), and employment support programs (Bellemare and Wichman forthcoming). [5]
As per Halvorsen and Palmquist (1980), adjustments to the point estimates are required to support interpretations that adhere strictly to the table's row descriptions. Except for scaling coefficients by factors of 10, I have presented the parameters in their raw form to facilitate a simpler crosscheck against the Santos Silva and Tenreyro paper. [6]
Petersen writes down the exact conditions under which arithmetic and geometric mean functions have different slope coefficients, and they are complicated. [7]
They also provide methods that are necessary to back out precise elasticities using these approaches. [8]
Using the authors' words, ‘Hospitalists are attending physicians who spend 3 months a year attending on the inpatient words [sic], rather than the 1 month a year typical of most academic medical centers’ (p 482). I report the estimates without ‘smearing factors’. [9]