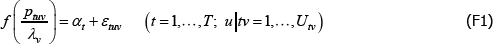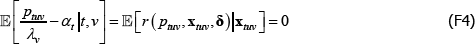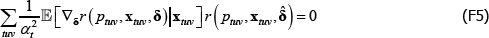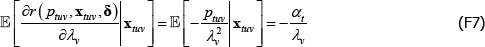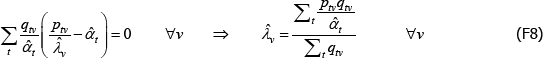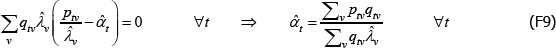RDP 2018-08: Econometric Perspectives on Economic Measurement Appendix F: The Method of Moments Makes Sensible Multilateral Index Functions
July 2018
- Download the Paper 1,726KB
Consider a model consisting of assumptions A1** to A4**. It is a special case of The Diewert Model.
A1**
where: f (·), ptuv, αt, εtuv and Utv are understood already; and λv is a fixed effect for varieties.
A2** Across varieties the observations are independently and identically distributed.
A3** The errors follow strict exogeneity of the form. So
A4** There is conditional heteroskedasticity of the form
where σ is some strictly positive constant.
Now consider a case that sets f (x) = x, Utv = qtvλv and 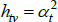 . As the model is in levels, the heteroskedasticity assumption is natural.
. As the model is in levels, the heteroskedasticity assumption is natural.
The model corresponds to the conditional moment restriction
where δ and xtv is vector shorthand for the full set of coefficients and regressors (the time and product dummies) that are implicit in the model, for a given (t, v) pair.
Following Wooldridge (2010, p 542), the efficient method of moments estimators for αt and λv solve
But note that
and
the last of which contains the unknown parameters α and λ. The feasible method of moments estimators use 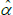 and
and 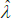 instead.
instead.
The resulting system of equations is
and
This is the same as the system of Geary (1958) and Khamis (1972). The result differs somewhat from the original method of moments derivation of Rao and Hajargasht (2016), who argue that an inefficient weighting system is necessary to generate the index. Although our set-ups are different, ultimately it is the introduction of units of equal interest that resolves the discrepancy.
Table F1 provides the settings needed to generate the other multilateral indices considered in Rao and Hajargasht (2016), using the method of moments. I have not explored whether there are further multilateral indices that fit the method of moments interpretation.
| Index name (year) | 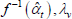 |
f(x) | Utv | htv |
|---|---|---|---|---|
| Dutot-style | 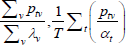 |
x | λv | 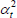 |
| Harmonic | 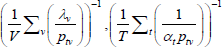 |
x−1 | 1 | 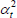 |
| Geometric | 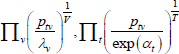 |
ln(x) | 1 | 1 |
| Geary (1958)–Khamis (1972) | 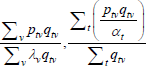 |
x | λvqtv | 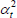 |
| Iklé (1972) | 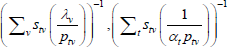 |
x−1 | ptvqtv | 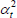 |
| Rao (1990) | 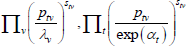 |
ln(x) | ptvqtv | 1 |
| Hajargasht and Rao (2010, type a) | 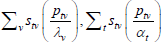 |
x | ptvqtv | 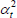 |
| Hajargasht and Rao (2010, type b) | 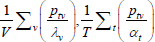 |
x | 1 | 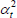 |