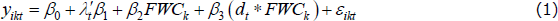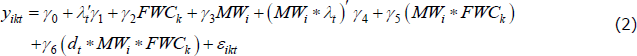Research Discussion Paper – RDP 2018-06 The Effect of Minimum Wage Increases on Wages, Hours Worked and Job Loss
1. Introduction
The effect of minimum wages on employment has been widely debated. Despite a vast research effort, economists remain divided on the issue. In Australia, these effects have been particularly difficult to quantify, in part due to Australia's complex system for setting minimum wages. Due to this lack of evidence, policymakers have tended to rely on the evidence for the United States and United Kingdom. However, as the Productivity Commission (2015b, p 190) has argued, we should be cautious in drawing lessons from the US and UK experiences, due to the ‘significantly different institutional wage setting arrangements and lower minimum wages’ in those countries compared to Australia.
This paper uses some of the unique institutional features of wage setting in Australia as an identification strategy to estimate the effects of minimum wage rises on wages, hours worked and the job destruction rate. To my knowledge, these are the first causal estimates of the effect of minimum wages on hourly wages in Australia. My analysis also adds to the limited evidence base on the effects of minimum wages on hours worked and the job destruction rate. I also make a methodological contribution, by proposing an identification strategy that is arguably better suited to Australian wage-setting institutions than those used in previous research. Finally, I use a new job-level dataset that provides several important advantages over other datasets that have been used previously in the Australian and international literatures.
The impact of minimum wages on employment remains contentious in the international literature. The empirical evidence often differs depending on the methodologies and datasets used. Economic theory also makes no clear predictions. Although the traditional competitive model of the labour market suggests that a minimum wage rise will reduce employment – if set above the market clearing wage – other theoretical models can predict the opposite. For example, an increase in the minimum wage could increase employment in a monopsony labour market (e.g. Card and Krueger 1994). Thus, there is a need for further empirical evidence on the relationship between minimum wages and employment, and in particular, credible evidence for Australia.
In Australia, up to 40 per cent of employees are directly or indirectly affected by the Fair Work Commission's (FWC) annual wage review.[1],[2] In part, this reflects that Australian minimum wages are high relative to other nations – both in absolute terms and as a share of median earnings (Leigh 2007). However, the large share of employees influenced by FWC decisions also reflects Australia's unique ‘awards’ system for setting wages, which often requires minimum wages that are higher than the national minimum wage (NMW). This paper provides estimates of several key parameters that are important in gauging the effects of these policy decisions.
Australia provides a useful laboratory for studying the effects of wage floors. Unlike other countries that set a single minimum wage (e.g. the United Kingdom, Germany and New Zealand) or a minimum wage that varies by state (e.g. the United States), Australia sets thousands of minimum wages that range from $18.29 per hour to as high as $165 per hour (as at 1 July 2017). These ‘award wages’ can depend on the industry, age, skill level, qualifications and location of an employee, plus a range of idiosyncratic factors.
To identify the causal effect of award wage increases on wages, hours worked and the job destruction rate, I focus on a unique period in Australian labour market history. Up until the late 2000s, the FWC was routinely announcing uniform dollar increases to all awards each year, regardless of their current level. This led to larger award wage rises in percentage terms for jobs whose award wages were relatively low, compared with those on higher award wages. Using job-level data from firms and a difference-in-differences strategy, I find that award changes are almost fully passed through to wages, and have no statistically significant effect on hours worked or the job destruction rate. These results are robust to controlling for wage group-specific shocks using a difference-in-difference-in-differences strategy and data on jobs whose pay is not set by awards.
A key advantage of my study is that I use job-level data that include both a precise measure of actual wages and an indicator for whether a job's wage is set according to a minimum or award wage. This allows me to focus on jobs directly affected by minimum wage decisions. This approach differs from much of the previous literature (particularly for the United States), which, due to data limitations, tends to focus on low-wage industries, such as the restaurant sector, or on lower-productivity employees, such as teenagers. Using low-wage groups as a proxy for employees reliant on minimum wages may lead to biased estimates of the effect of minimum wages on employment (Jardim et al 2017).
The job-level data I use also allow me to study the effect of changes to minimum wages on hourly wages themselves, which is rarely possible. The pass-through of award wages to hourly wages is a key consideration for the FWC in terms of assessing whether firms are complying with their legal obligations. The elasticity of hourly wages with respect to minimum wages is also one of the key parameters in assessing the effect of minimum wage increases on income inequality (Leigh 2007).
The remainder of this paper is structured as follows. Section 2 briefly discusses previous work on the effect of minimum wages on employment. Section 3 provides some background on Australia's system of award wages. Section 4 describes the natural experiment. The empirical strategy and data are described in Sections 5 and 6, respectively. Sections 7 and 8 present the empirical results and robustness tests, and Section 9 provides some concluding remarks.
2. Previous Literature
Most credible studies on the effects of minimum wages on employment have been conducted for the United States. Starting with the seminal contribution of Card and Krueger (1994), these US studies tend to focus on state variations in minimum wages. In these studies, estimates of the effect of minimum wages on employment vary in magnitude as well as in direction (Doucouliagos and Stanley 2009; Dube, Lester and Reich 2010; Sawhill and Karpilow 2014). In saying that, there has been some convergence in the range of estimates over time, with most studies finding a small negative effect of minimum wages on employment, or zero effect. In light of this large body of evidence, the US Congressional Budget Office (2014) adopts a ‘central estimate’ that a 10 per cent increase in minimum wages reduces employment among affected workers by up to 1 per cent. Nevertheless, some prominent researchers maintain that minimum wages have significant adverse effects on employment and hours worked (e.g. Neumark 2014; Jardim et al 2017).
Leigh (2003) adapted this identification strategy to Australian data. He uses the fact that between 1994 and 2001 there were six changes to Western Australia's (WA) minimum wage, of between 3.5 and 9.3 per cent, that occurred out-of-step with other states. Leigh compared changes in the employment-to-population ratio in WA with those for the rest of the country around each of these changes. Across the workforce as a whole, he found an elasticity of employment with respect to the minimum wage of −0.29. He also found that the effects were greatest for workers aged 15–24, who had an employment elasticity of −1.0. However, there are some concerns about the methodology and robustness of Leigh's results (Junankar 2004; Watson 2004), and scepticism about the magnitude of these effect sizes (Neumark and Wascher 2006).
Research on the effects of minimum wages in the United Kingdom has tended to use different control strategies, given the lack of variation in minimum wages across geographic areas. Studies typically compare workers directly affected by changes in the NMW with a ‘control’ group of workers not directly affected – notably, those higher up the wage distribution (e.g. Dickens and Draca 2005; Dickens, Riley and Wilkinson 2009, 2012; Bryan, Salvatori and Taylor 2013). These studies find little evidence that either the introduction of the NMW in 1999 or subsequent increases to the NMW had an adverse effect on employment. The Productivity Commission (2015a) has since applied a similar identification strategy to Australia.[3] Using administrative data for the period 2008 to 2013, they studied employment transitions around FWC decisions using a difference-in-differences strategy. Their approach was similar to the UK research, with workers earning wages higher up the wage distribution used as a control, and workers ‘captured’ by the increase used as the treatment group. They found that adverse employment effects from minimum wage increases are felt more by ‘would-be employees’ (that is, the unemployed and those outside the labour force). For those in jobs, the main effect was a reduction in hours worked rather than job loss. However, the Productivity Commission has expressed concerns about the robustness of these results.
3. Minimum Wages Policy in Australia
The operation of Australian minimum wages is notoriously complex (Leigh 2007). In Australia the NMW sets a legal floor on wages. As of 1 July 2017, this was equal to $18.29 per hour for a full-time adult employee. Australia also has a detailed system of award wages that are layered on top of the NMW; this is in contrast to most other countries, which tend to have a single minimum wage.[4] The Australian awards often set a different minimum wage depending on an employee's age, skill, industry and location. For example, an employee who supervises lift operators at a ski resort is entitled to a wage of $23.80 per hour, 30 per cent above the NMW. As such, while many employees are paid the NMW – particularly lower-skilled workers and those not covered by an award or enterprise agreement – many others are entitled to a higher wage. The distribution of these award wages across different job classifications is shown in Figure 1.
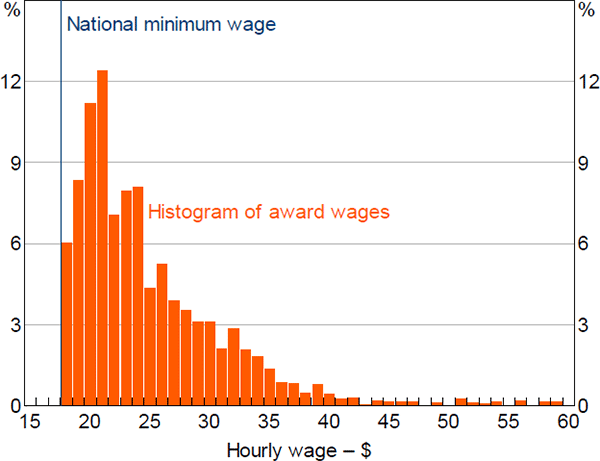
Notes: Ordinary time base wage rates for full-time adult employees; excludes wages above $60 per hour
Sources: Author's calculations; Fair Work Ombudsman
The NMW and all award wages are adjusted at the same time every year, usually in early July. The size of these adjustments is decided at a national level by the FWC. Adjustments are applied consistently across awards; historically the FWC has either added a flat dollar amount to all award wages (1993–2010) or raised all award wages by the same percentage amount (2011–2017). Adjustments to individual awards are rare, and are seldom made in response to industry-level demand shocks. Indeed, an award-specific adjustment is only made to ensure an award is consistent with the principle of ‘equal remuneration for work of equal or comparable value’, to remove an ambiguity or to correct an error (Stewart 2015).[5]
Australia's detailed system of awards has generally been seen as an impediment to estimating the effects of minimum wages in Australia (Lee and Suardi 2011; Productivity Commission 2015a). This is certainly true when researchers have simply tried to apply methodologies developed in the United States and United Kingdom to Australian data. But this should not be surprising; such methodologies were designed for countries with very different wage-setting institutions. For example, studies that attempt to define a control group as individuals paid slightly above the NMW – as is common in UK research – face the issue that such employees are potentially caught up in the awards system, and hence are not a valid control given that awards are adjusted at the same time as the NMW each year. Indeed, when using this approach the Productivity Commission (2015a) found evidence that their control group was contaminated by these spillovers.
In contrast to previous Australian studies, I treat Australia's complicated system of awards as a unique source of variation in minimum wages, rather than a factor that complicates identification. In particular, I exploit changes to the entire distribution of minimum and award wages stemming from FWC decisions. This not only provides additional variation with which to estimate the relevant effects, but it also makes it much clearer who the control group actually are.
4. Flat Dollar Adjustments over 1998–2008
The decade leading up to 2008 is useful for studying the effects of award wages on other labour market outcomes. During this period, the FWC were routinely granting flat dollar increases to all awards each year, irrespective of the existing wage rates contained in those awards. For example, in May 2000, the FWC increased all award wages by 39 cents per hour.[6] This meant that employees on relatively low award wages received larger wage increases in percentage terms than those on higher award wages.
Figure 2 shows the percentage increase in award wages in each year from 1998 to 2008 across different award wage levels. The flat dollar increases are what generates the downward slope in each profile. On some occasions the FWC also granted smaller flat dollar increases to higher award wage ranges, rather than a single flat dollar increase. For example, in 2003, the FWC announced an increase of 45 cents per hour for all award wages up to $19.26 per hour, and 39 cents per hour for all wages above this level. This created a discontinuity in the profile of percentage wage increases at $19.26 per hour (Figure 2). These discontinuities tend to exacerbate the differences in the size of the award wage increase between low- and high-award-wage employees. The only exception was in 2001, when the FWC awarded a series of larger flat dollar increases to higher award-wage earners. Further details on each decision are available in Appendix A.
The decision to announce flat dollar increases each year (and often in smaller amounts to higher wage brackets) led to a significant compression of the distribution of minimum wages over time. This was a deliberate policy decision intended to ‘allocate the greater share of wage rises to those in greatest need’ (FWA 2011, p 61). The rationale was that a flat dollar increase gave ‘appropriate emphasis to the needs of the low paid whilst moderating the overall economic impact’ of the minimum wage decision (AIRC 2003). Policymakers also sought to encourage higher wage earners to negotiate wages directly with firms, rather than remain on awards, and believed that granting smaller wage rises would encourage this to happen (AFPC 2006).
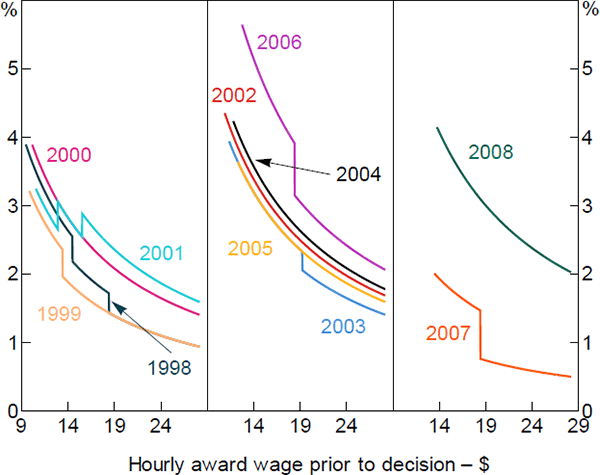
Sources: Author's calculations; Fair Work Ombudsman
Although the FWC had been announcing flat dollar increases to all awards as early as 1993, I focus on the period after 1998 due to data availability. I also omit the flat dollar increase announced in 2010 from my analysis as it may lead to results that are contaminated by the effects of award modernisation.[7] Since 2011, the FWC has been granting flat percentage increases to all awards each year (in addition to any adjustments associated with award modernisation between 2010 and 2014), thus preserving the existing wage differentials between awards.
5. Empirical Strategy
I focus on jobs paid exactly an award wage prior to each FWC decision. I do this to obtain direct estimates of the effects on the population of interest (award-wage earners) and because I can only infer the relevant award wage adjustment for this group. As discussed earlier, this approach differs from most of the previous literature, which tends to focus on groups that are likely to be most affected by minimum wages changes, such as restaurant staff and youths.
I use a difference-in-differences (DD) model to estimate the effects of award wage changes on wages, hours worked and the job destruction rate. The size of the ‘treatment’ in this model is governed by a continuous variable that measures the percentage change in wages that an award-reliant employee should receive, given their wage level immediately prior to the decision. This DD model simply compares the change in each outcome variable – wages, hours worked or job destruction – around each FWC decision between jobs that experienced a relatively large percentage increase in their award wage and those that experienced a relatively small increase.
Rather than consider the 11 decisions between 1998 and 2008 individually, I pool them together and use a single DD estimator that constrains the coefficient of interest to be constant across the decisions. This maximises the available sample that I have to estimate the elasticities of interest. The DD equation is,
where yikt is the dependent variable of interest for job i in wage group k at time t.[8] λt is a full set of time dummies that control for any macro shocks that affect all wage groups in any of the 22 time periods (there are 11 different FWC decisions each with their own ‘before’ and ‘after’ period). FWCk is the log change in award wages for wage group k due to the FWC decision. There are also a set of interactions between FWCk and dt, the latter being a dummy that takes the value of zero in the ‘before’ period immediately prior to an award increase and a value of one in the ‘after’ period six months later. The coefficient of interest is β3. When the dependent variable is the log hourly wage (or log hours worked), this DD coefficient is the elasticity of wages (or hours) with respect to the award wage, a parameter of key interest to policymakers.
In addition to constraining the DD coefficient to be constant across each of the FWC decisions, Equation (1) also restricts the effects of group-specific heterogeneity (as captured by FWCk) to be constant across each decision. Relaxing this assumption, and allowing for a more flexible control for the group-specific heterogeneity, has very little impact on the results (see Section 8.1).
6. Data And Descriptive Statistics
6.1 Data
I estimate Equation (1) using job-level data from the Australian Bureau of Statistics (ABS) Wage Price Index (WPI) survey. This survey includes 3,000 firms per quarter, with each firm being surveyed every quarter for five years, before being rotated out of the sample (roughly one-fifth of the sample is replaced each year). After being selected into the sample, a firm is asked to randomly select a certain number of jobs from their payroll records. The firm then reports information on each of these jobs over time. Around 18,000 jobs are included in the survey every quarter. Approximately 15–20 per cent of these jobs have their pay set exactly according to an award.
The WPI survey follows jobs, rather than employees (for example, a graduate economist at the Reserve Bank of Australia in the middle of the performance range). If the occupant of the job leaves the firm or moves to a different job within the firm, the ABS substitutes the job leaver with the employee who replaced her or an existing employee with the same job title. For this reason, my unit of analysis is the job.
My estimation sample includes all private sector jobs filled by an adult on an award rate. I exclude juniors, apprentices and trainees from my analysis, as it is too difficult to accurately infer their award wage adjustment. This is unfortunate because these groups may be particularly vulnerable to job loss following an increase in award wages. I also exclude jobs not within the scope of the federal industrial relations system after 2006, due to the uncertainty about what award wage adjustments such jobs experienced during this period of industrial relations reform. After these sample restrictions, I am left with a sample of 32,174 job-period observations spanning the 11 decisions over the period between 1998 and 2008. The key outcome variables I consider are:
- Wages: the log of the job's hourly wage, excluding any wage changes due to changes in the job occupant's grade or performance.
- Hours worked: the log of the ordinary-time hours paid for during the most recent pay period. This includes hours of paid leave (e.g. annual leave and sick leave) but excludes overtime hours.
- Job destruction rate: a binary variable that equals one if job i had ceased by survey date t, conditional on the job existing six months earlier, and zero otherwise. This captures both redundancies and firm failure.
The estimates for wages and hours worked are conditional on the job being in the sample in the before period and after period for a given FWC decision. If a job is vacant or made redundant in either period it is dropped from the sample. This is not the case for the job destruction rate.
6.2 Descriptive Statistics
The award wage that applies to a job is typically a function of a number of factors, including the job's industry, skill requirements and location. To see how these job characteristics vary over the distribution, Table 1 presents the means of several variables at each decile of the award wage distribution. The mean hourly wage of jobs ranges from $13.80 in the lowest decile to $32.00 in the top decile (in 2009 dollars). Jobs in lower wage deciles are more likely to be casual, less skilled, with shorter working hours, and in smaller firms, relative to those in higher deciles. Award-wage earners are over-represented in certain industries, with the overall industry distribution in my sample broadly consistent with data from the ABS's survey of Employee Earnings and Hours.
| Wage decile | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Hourly wage ($)(a) | 13.8 | 14.6 | 15.0 | 15.4 | 15.8 | 16.4 | 17.2 | 18.3 | 20.7 | 32.0 |
| Casual share (%) | 56.5 | 40.1 | 31.8 | 45.6 | 43.6 | 29.8 | 23.9 | 21.6 | 16.8 | 6.1 |
| Weekly hours worked(b) | 26.3 | 26.1 | 28.0 | 27.0 | 27.3 | 29.4 | 28.9 | 28.9 | 30.0 | 31.1 |
| Firm size (employees)(c) | 324 | 357 | 346 | 384 | 324 | 338 | 378 | 348 | 370 | 502 |
| Low skill share (%)(d) | 57.2 | 68.6 | 57.7 | 47.4 | 41.5 | 27.6 | 38.5 | 28.0 | 15.4 | 1.1 |
| Industry shares (%) | ||||||||||
| Manufacturing | 7.3 | 5.0 | 5.1 | 3.2 | 2.5 | 5.1 | 3.4 | 2.8 | 2.0 | 1.2 |
| Retail | 9.4 | 4.2 | 13.0 | 10.5 | 16.9 | 11.3 | 5.7 | 3.8 | 3.6 | 1.5 |
| Accomm, cafes & restaurants | 32.3 | 31.8 | 25.8 | 41.9 | 16.7 | 16.9 | 15.5 | 18.2 | 11.6 | 3.0 |
| Property & business services | 11.5 | 29.3 | 14.4 | 10.6 | 12.4 | 10.8 | 25.7 | 19.1 | 16.7 | 5.8 |
| Health & community services | 11.1 | 7.9 | 14.9 | 18.8 | 27.0 | 25.2 | 22.4 | 26.3 | 32.2 | 39.7 |
| Cultural & recreational services | 7.6 | 4.1 | 3.3 | 1.3 | 2.1 | 3.1 | 3.3 | 4.9 | 5.1 | 2.4 |
| Personal & other services | 9.1 | 6.4 | 5.5 | 2.9 | 3.8 | 8.6 | 6.7 | 7.8 | 9.7 | 11.2 |
| All other | 11.7 | 11.3 | 18.0 | 10.7 | 18.6 | 18.9 | 17.4 | 17.0 | 19.1 | 35.1 |
|
Notes: (a) In 2009 Australian dollars, deflated using consumer price index; excludes casual loading |
||||||||||
7. Results
7.1 Baseline Estimates
The baseline estimates for wages, hours worked and the job destruction rate are shown in Table 2. I present separate estimates using the full sample and a sample that omits the first four FWC decisions (1998–2001). Although the sample size is larger for the full sample, there is a data issue prior to 2002 that could potentially distort the regression results.[9]
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| 1998–2008 sample | 0.84*** (0.03) |
0.26 (0.37) |
−0.22 (0.44) |
| 2002–08 sample | 0.93*** (0.04) |
0.13 (0.47) |
−0.37 (0.55) |
| Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively | |||
I find strong evidence that award adjustments are passed on to wages. Using the full sample, I estimate the elasticity of wages with respect to the award wage to be 0.84 and highly statistically significant.[10] This estimate is larger in the shorter sample period – 0.93 – which suggests that measurement issues in the first few years of data may be attenuating the size of the overall elasticity in the full sample.[11] The results suggest less-than-full pass-through of FWC decisions to wages. The hypothesis that the wage elasticity is equal to one can be rejected at the 1 and 10 per cent levels of significance using the 1998–2008 and 2002–08 samples, respectively. This may reflect some degree of non-compliance by firms in their legal obligations (see Productivity Commission (2015a, p 12) for a discussion), or simply measurement error. In any case, the elasticity is sufficiently close to one to characterise this as near-complete pass-through.
Having established that award wage increases are passed through to wages, the next step is to see if this leads to any reductions in hours worked or job loss. I find no evidence that award changes have an adverse effect on hours worked (Table 2).[12] In fact, the DD estimate is positive, suggesting that jobs with larger award wage rises had larger increases in hours worked than jobs experiencing a smaller award wage rise. Based on the 95 per cent confidence interval, I am able to rule out adverse effects on hours worked that are larger (in absolute value) than −0.46.[13] I also find that award wage increases do not have a statistically significant effect on the job destruction rate (Table 2). Again, if anything, the point estimates suggest that the job destruction rate actually declines when the award wage is increased.
7.2 Difference-in-difference-in-differences
Like any analysis using difference-in-differences, my results are sensitive to violations of the so called ‘parallel trends’ assumption. The assumption is that in the absence of a change in award wages, the wages, hours worked and probability of job loss of low-award-wage workers would have followed the same trajectory as high-award-wage workers. This would be violated if, say, there is a change in tax policy that affects low-wage earners relatively more than high-wage earners that occurs at the same time as the change in award wages. If this happens, we may incorrectly attribute the effect of the tax change to the award wage. This assumption is often examined by looking at pre-treatment trends across the treatment and control groups. I do not have sufficient pre-treatment data to allow me to perform such a test.
Instead, I implement a difference-in-difference-in-differences (DDD) approach to address any concerns about violations of the parallel trends assumption. The idea of this approach is to use low- and high-wage jobs whose wages are set according to enterprise bargaining agreements (EBAs) as an additional control group. These jobs are paid wages above the legal minima that are contractually ‘locked-in’ for a specified period of time, and thus are not affected by the award wage decisions.[14]
Conceptually, this DDD approach involves estimating a separate DD model using jobs whose pay is set by an EBA. The wage levels of these jobs are used to infer what wage adjustment they would have had had their pay been set by an award (this is the size of the ‘treatment’ experienced by this group). I then subtract these estimates from the baseline DD estimates to adjust the latter for any shocks that differentially affect low-wage jobs. For example, say there is a shock in the after period that only affects low-wage jobs. The baseline DD estimates will be biased. However, if the shock has the same effect on the low-wage jobs on EBAs, then the DDD model will fully absorb the effect of that shock. The DDD specification is as follows,
where MWi is a dummy variable that equals one if the job's pay is set according to an award, and zero otherwise (the base category is jobs whose pay is set according to an EBA). The coefficient of interest is the coefficient on the third-level interaction (γ6), which provides the DDD estimate of the effect of a change in award wages on the outcome variable yikt for award-reliant jobs. The model is estimated on the combined sample of jobs paid an award and jobs covered by EBAs.
The results suggest that the baseline estimates are robust to controlling for violations of the parallel trends assumption (Table 3). For wages, the DD estimates for the EBA sample are close to zero and hence the results of the DDD model are very similar to the baseline DD model. The fact that award wage decisions do not spill over to jobs on EBAs suggests that the baseline estimates for wages are not being driven by wage group-specific shocks. It also indicates that jobs on EBAs are an appropriate control group. The results for hours worked and the job destruction rate are also robust to controlling for wage growth-specific shocks using the DDD model.
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| 1998–2008 sample | |||
| (A) DD for awards | 0.84*** (0.03) |
0.26 (0.37) |
−0.22 (0.44) |
| (B) DD for EBAs | 0.03 (0.02) |
0.09 (0.21) |
0.14 (0.24) |
| (A – B) DDD | 0.81*** (0.03) |
0.17 (0.42) |
−0.36 (0.50) |
| 2002–08 sample | |||
| (A) DD for awards | 0.93*** (0.04) |
0.13 (0.47) |
−0.37 (0.55) |
| (B) DD for EBAs | 0.01 (0.02) |
0.01 (0.24) |
0.35 (0.27) |
| (A – B) DDD | 0.92*** (0.04) |
0.12 (0.53) |
−0.72 (0.61) |
|
Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively |
|||
7.3 Placebo Test
Another way to assess the validity of the parallel trends assumption is to do a placebo test using the FWC decision that immediately followed our estimation period of 1998–2008. In 2009, the FWC unexpectedly froze all minimum and award wages due to concerns about rising unemployment during the global financial crisis. Because there was no change in award wages in this decision, finding evidence of a casual effect on other labour market variables may indicate misspecification. I generate a ‘placebo treatment’ by assuming that the FWC had actually granted a flat increase of 57 cents per hour in 2009, which was the size of the increase in 2008. I find no evidence of any placebo effect when estimating the DDD model for the 2009 FWC decision (Table 4). This provides added confidence that the parallel trends assumption is valid.
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| (A) DD for awards | −0.22* (0.12) |
−0.06 (1.76) |
3.04* (1.66) |
| (B) DD for EBAs | −0.22*** (0.05) |
0.58 (0.85) |
2.59*** (0.74) |
| (A – B) DDD | 0.01 (0.13) |
0.64 (1.95) |
0.44 (1.84) |
| Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively | |||
7.4 Constant Elasticity Assumption
The interpretation of the results in Tables 2 and 3 as causal effects assumes that the elasticities of hours worked and job loss with respect to the minimum wage are constant throughout the distribution of skills. Some studies find that the employment of lower-skilled workers is more sensitive to minimum wage changes than higher-skilled workers (Gindling and Terrell 2007). If this were true, it would bias us toward estimating employment effects that are larger (i.e. more adverse) than the ‘true’ effect. Given that I found no discernible effect of award wages on hours worked or the job destruction rate, the likely sign of the bias reinforces the conclusion that award wage increases do not have large adverse employment effects.
8. Robustness Checks
I now consider a set of robustness checks on the baseline DD and DDD models. These tests are described in Sections 8.1–8.4 below, with the results for the full sample presented in Table 5.
8.1 Different Controls for Unobserved Group Effects
The baseline models assume that the effects of group-specific heterogeneity are linear (as captured by the continuous FWCk control). A more flexible parametisation is to use separate dummy variables for each award wage decile prior to FWC decisions. The baseline models also impose that the effects of group-specific heterogeneity are constant across each of the 11 FWC decisions. I relax both of these assumptions by including a set of wage decile dummies, along with interactions between these dummies and a set of dummy variables for each of the 11 FWC decisions (Table 5). The results are very similar to the baseline model.
| Wages (%) |
Hours worked (%) |
Job destruction rate (ppt) |
|
|---|---|---|---|
| Different controls for unobserved group effects | |||
| DD | 0.84*** (0.03) |
0.26 (0.37) |
−0.35 (0.57) |
| DD for EBAs | 0.03 (0.02) |
0.09 (0.21) |
0.42 (0.28) |
| DDD | 0.81*** (0.03) |
0.17 (0.42) |
−0.77 (0.60) |
| Excluding jobs in Queensland | |||
| DD | 0.82*** (0.03) |
0.18 (0.44) |
0.03 (0.45) |
| DD for EBAs | 0.01 (0.02) |
0.05 (0.29) |
0.19 (0.27) |
| DDD | 0.81*** (0.04) |
0.12 (0.53) |
−0.16 (0.53) |
| Adjusting for pre-trends | |||
| DD | 1.26*** (0.05) |
1.08* (0.64) |
na na |
| DD for EBAs | 0.17*** (0.03) |
−0.15 (0.36) |
na na |
| DDD | 1.08*** (0.05) |
1.24* (0.73) |
na na |
| Controlling for firm-specific shocks | |||
| DD | 0.73*** (0.05) |
−0.94* (0.97) |
−0.47 (0.71) |
| Notes: Standard errors (in parentheses) are clustered at the individual job level; ***, ** and * denote statistical significance at the 1, 5 and 10 per cent levels, respectively | |||
8.2 Excluding Jobs in Queensland
My baseline results also assume that award wages are adjusted shortly after the FWC announcement. However, employees on certain state awards experienced a lag in the adjustment of their award wage due to a delay by their state industrial relations commission in ratifying the national decision.[15] This was particularly true for employees in Queensland, which was slower than the other states to ratify the increases in 2003, 2004 and 2005. My results are robust to excluding all jobs in Queensland from the sample (Table 5).
8.3 Adjusting for Pre-trends
I also consider the robustness of the baseline estimates to re-specifying the dependent variable in Equations (1) and (2) to be in terms of log changes over the previous six months, rather than in log levels. This specification will compare growth in, say, wages in the period immediately before the FWC decision with growth in wages over the six months after the FWC decision, across low-wage and high-wage jobs. This type of ‘triple differencing’ approach is common in UK studies of minimum wages (Dickens et al 2009; Bryan et al 2013). An advantage of this approach is that it controls for the possibility that the labour market outcomes of low-wage and high-wage jobs had different trajectories in the lead-up to each decision. However, I find that re-specifying the dependent variable in this way makes little difference to the findings (Table 5). Results are not presented for the job destruction rate, which is already constructed using transitions over six-month windows.
8.4 Controlling for Firm-specific Shocks
An alternative approach to controlling for violations of the parallel trends assumption is to augment Equation (1) with a full set of firm dummies, and interactions between these dummies and the after period dummy, dt. This specification only uses variation within firms to identify the DD coefficient of interest, and thus controls for many potential violations of the parallel trends assumption (for example, a shock in the after period that disproportionately affects low-wage industries). The estimated wage elasticity (0.73) is slightly lower than in the baseline model (Table 5). For hours worked and the job destruction rate, the standard errors on the coefficients of interest are several times larger than in the baseline model, which limits the conclusions that can be drawn.
9. Discussion
There is widespread interest in understanding the effects of minimum wage increases. I add to the evidence base by using an identification strategy uniquely suited to Australia and a dataset that provides several advantages over those used previously in the literature. I provide the first causal estimates of the effect of minimum wages on wages in Australia, and one of the few credible estimates of the effects on hours worked and job loss. I find that small, incremental adjustments to awards are mostly passed on to wages in award-reliant jobs. These adjustments appear to have little adverse effect on hours worked or job loss. These findings are consistent with the international evidence and the FWC's (2017) current assessment of that evidence base.[16]
There are several things to keep in mind when interpreting these findings. Firstly, as discussed earlier, my results are for adult employees only and do not include juniors. Secondly, the results may not necessarily generalise to large, unanticipated changes in award wages. There will always be some point at which a minimum wage adjustment will begin to reduce employment. Thirdly, my paper studies fairly tight windows around FWC decisions, and thus gives valid estimates of the effect of the minimum wage on hours worked and job loss only if employers take less than six months to adjust to changes in the award wage (Borland 2018). Finally, although I find no statistically significant evidence of an effect of award adjustments on job destruction, this does not rule out an adverse effect on employment. For instance, the adverse consequences of higher wage floors may be borne by job seekers, rather than job holders. Evidence from the Productivity Commission (2015a, p 67) tentatively supports this possibility.
Australia's rich tapestry of minimum wages provides other avenues for future work. Given that award wages are set at many levels throughout the distribution of wages, marginal effects could be estimated at multiple minimum wage levels. This could contribute to our understanding of the optimal level of the minimum wage.
Appendix A: Summary of Minimum Wage Decisions
| Year | Increase in hourly wage(a) | Range of award wages to which increase applied | Date announced | Date effective(b) | Before period(c) | After period(c) |
|---|---|---|---|---|---|---|
| 1998 | 37 cents | Less than $14.47 per hour | May 1998 |
May 1998 |
1998:Q2 | 1998:Q4 |
| 32 cents | Between $14.47 per hour and $18.42 per hour | |||||
| 26 cents | Greater than $18.42 per hour | |||||
| 1999 | 32 cents | Less than $13.42 per hour | 29 April 1999 |
29 April 1999 |
1999:Q2 | 1999:Q4 |
| 26 cents | Greater than $13.42 per hour | |||||
| 2000 | 39 cents | All awards | 1 May 2000 |
1 May 2000 |
2000:Q2 | 2000:Q4 |
| 2001 | 34 cents | Less than $12.89 per hour | 2 May 2001 |
2 May 2001 |
2001:Q2 | 2001:Q4 |
| 39 cents | Between $12.89 per hour and $15.52 per hour | |||||
| 45 cents | Greater than $15.52 per hour | |||||
| 2002 | 47 cents | All awards | 9 May 2002 |
9 May 2002 |
2002:Q2 | 2002:Q4 |
| 2003 | 45 cents | Less than $19.26 per hour | 6 May 2003 |
6 May 2003 |
2003:Q2 | 2003:Q4 |
| 39 cents | Greater than $19.26 per hour | |||||
| 2004 | 50 cents | All awards | 5 May 2004 |
5 May 2004 |
2004:Q2 | 2004:Q4 |
| 2005 | 45 cents | All awards | 7 June 2005 |
7 June 2005 |
2005:Q2 | 2005:Q4 |
| 2006 | 72 cents | Less than $18.42 per hour | 27 October 2006 |
1 December 2006 |
2006:Q4 | 2007:Q2 |
| 58 cents | Greater than $18.42 per hour | |||||
| 2007 | 27 cents | Less than $18.42 per hour | 5 July 2007 |
1 Octobe 2007 |
2007:Q3 | 2008:Q1 |
| 14 cents | Greater than $18.42 per hour | |||||
| 2008 | 57 cents | All awards | 8 July 2008 |
1 October 2008 |
2008:Q3 | 2009:Q1 |
Notes: State and federal industrial relations systems prior to 2006 and federal system after 2006; all announcement and effective dates are for the federal system
(a) Where relevant, weekly award rates are converted to hourly rates by assuming a 38-hour work week and rounding to the nearest cent
(b) Between 1998 and 2005, the decision was effective immediately (upon application by a union for a change to be made to the award) provided that at least 12 months had passed since the date of the last variation to the award; the new minimum wage rates take effect on the first full pay period commencing on or after the effective/operative date
(c) Before and after periods refer to the timing of the WPI surveys used in the regression analysis
References
AFPC (Australian Fair Pay Commission) (2006), ‘Wage-Setting Decision and Reasons for Decision’, October.
AIRC (Australian Industrial Relations Commission) (2003), ‘Safety Net Review – Wages 6 May 2003, Decision’, PR002003.
Borland J (2018), A Review of Methods Applied in International Research on the Employment Effects of the Minimum Wage and Implication for Australian Research, Fair Work Commission Research Report 4/2018, Fair Work Commission, Canberra.
Bryan M, A Salvatori and M Taylor (2013), ‘The Impact of the National Minimum Wage on Earnings, Employment and Hours through the Recession’, A Report to the Low Pay Commission by the Institute for Social and Economic Research, University of Essex.
Card D and AB Krueger (1994), ‘Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania’, The American Economic Review, 84(4), pp 772–793.
Congressional Budget Office (2014), ‘The Effects of a Minimum-Wage Increase on Employment and Family Income’, Report, February.
Dickens R and M Draca (2005), ‘The Employment Effects of the October 2003 Increase in the National Minimum Wage’, Centre for Economic Performance CEP Discussion Paper No 693.
Dickens R, R Riley and D Wilkinson (2009), ‘The Employment and Hours of Work Effects of the Changing National Minimum Wage’, Research Report prepared for the Low Pay Commission, March.
Dickens R, R Riley and D Wilkinson (2012), ‘Re-Examining the Impact of the National Minimum Wage on Earnings, Employment and Hours: The Importance of Recession and Firm Size’, Research Report prepared for the Low Pay Commission, January.
Doucouliagos H and TD Stanley (2009), ‘Publication Selection Bias in Minimum-Wage Research? A Meta-Regression Analysis’, British Journal of Industrial Relations, 47(2), pp 406–428.
Dube A, TW Lester and M Reich (2010), ‘Minimum Wage Effects across State Borders: Estimates Using Contiguous Counties’, University of California, Berkeley, Institute for Research on Labor and Employment, IRLE Working Paper No 157-07.
FWA (Fair Work Australia) (2011), ‘Decision – Annual Wage Review 2010–11’, [2011] FWAFB 3400.
FWC (Fair Work Commission) (2017), ‘Decision – Annual Wage Review 2016–17’, [2017] FWCFB 3500.
Gillard J (2008), ‘Request under Section 576C(1) — Award Modernisation’, Request from Minister for Employment and Workplace Relations to the President of the Australian Industrial Relations Commission, 28 March.
Gindling TH and K Terrell (2007), ‘The Effects of Multiple Minimum Wages Throughout the Labor Market: The Case of Costa Rica’, Labour Economics, 14(3), pp 485–511.
Jardim E, MC Long, R Plotnick, E van Inwegen, J Vigdor and H Wething (2017), ‘Minimum Wage Increases, Wages, and Low-Wage Employment: Evidence from Seattle’, NBER Working Paper No 23532.
Junankar PN (2004), ‘“Employment Effects of Minimum Wages: Evidence from a Quasi-Experiment”, by Andrew Leigh: A Preliminary Critique’, in ‘Minimum Wages Case 2004: Composite Exhibit’, Initial Submission by ACTU to Safety Net Review 2004, February, pp 65–68.
Lee W-S and S Suardi (2011), ‘Minimum Wages and Employment: Reconsidering the Use of a Time Series Approach as an Evaluation Tool’, British Journal of Industrial Relations, 49(s2), pp s376–s401.
Leigh A (2003), ‘Employment Effects of Minimum Wages: Evidence from a Quasi-Experiment’, The Australian Economic Review, 36(4), pp 361–373.
Leigh A (2007), ‘Does Raising the Minimum Wage Help the Poor?’, Economic Record, 83(263), pp 432–445.
Neumark D (2014), ‘Employment Effects of Minimum Wages’, Institute of Labor Economics, IZA World of Labor, May.
Neumark D, M Schweitzer and W Wascher (2004), ‘Minimum Wage Effects throughout the Wage Distribution’, The Journal of Human Resources, 39(2), pp 425–450.
Neumark D and W Wascher (2006), ‘Minimum Wages and Employment: A Review of Evidence from the New Minimum Wage Research’, NBER Working Paper No 12663.
Productivity Commission (2015a), Exploring the Effects of Minimum Wage Increases on Employment Using a Large Administrative Dataset, Workplace Relations Framework – Technical Supplement, Productivity Commission, Canberra.
Productivity Commission (2015b), Workplace Relations Framework: Volume 1, Final Report, Productivity Commission Inquiry Report No 76, Productivity Commission, Canberra.
Sawhill I and Q Karpilow (2014), ‘Raising the Minimum Wage and Redesigning the EITC’, Brookings Institution Report, 30 January.
Stewart A (2015), Stewart's Guide to Employment Law, 5th edn, The Federation Press, Annandale.
Watson I (2004), ‘Minimum Wages and Employment: Comment’, The Australian Economic Review, 37(2), pp 166–172.
Wright S and J Buchanan (2013), Award Reliance, Research Report 6/2013, Fair Work Commission, Melbourne.
Footnotes
Data from the survey of Employee Earnings and Hours (ABS Cat No 6306.0) suggest that 22.7 per cent of employees had their wage set according to an award wage in 2016. I refer to these as ‘award-reliant’ employees. The Award Reliance Survey for 2012/13 suggests that a further 21 per cent of employees had their wages influenced in a mechanical way by FWC decisions (Wright and Buchanan 2013). [1]
The FWC is an independent body with responsibility for adjusting minimum and award wages. The FWC began operation on 1 July 2009 (named Fair Work Australia), after assuming responsibility for award wage-setting from the Australian Fair Pay Commission (established in 2005) and the Australian Industrial Relations Commission prior to that. Throughout this paper, I use ‘FWC’ to refer to any of the various national and state industrial relations commissions with responsibility for setting award wages since the late 1990s. [2]
There have been several other Australian minimum wage studies. These studies often have data or other limitations that make their findings difficult to interpret (see Borland (2018) or Productivity Commission (2015b, Appendix C) for a review). [3]
New Zealand once had a system of awards similar to Australia's, but that system was abandoned in 1991. Although some countries have skill-based tiers of minimum wages, these generally use very broad tiers. For example, Hungary sets separate minimum wages for skilled and unskilled workers. [4]
Occasionally an industry will apply for a deferral in the annual award increase for their industry if they are facing exceptional circumstances and can demonstrate incapacity to pay. A common case is in the agricultural sector, which has often applied for a deferral due to drought. I have not included the agricultural sector in my analysis. [5]
The FWCs award adjustments were often stated in terms of a flat dollar increase to the full-time weekly award wage. Since weekly standard hours vary slightly from award to award, all references to hourly rates in this paper assume a 38-hour workweek. [6]
In 2010, the FWC began a process of consolidating 1,500 ‘pre-modern awards’ into 122 ‘modern awards’. The main objective of this award modernisation process was to reduce the regulatory burden on firms by creating a set of awards that were ‘simple to understand and easy to apply’ (Gillard 2008, p 1). [7]
A wage group is defined as any job paid a certain wage. For example, all jobs paid $20 per hour will be one group. [8]
This data issue relates to the fact that I cannot perfectly observe whether a job was paid according to an award prior to 2002. For this period, I could only identify the job's pay-setting mechanism (e.g. award or enterprise bargaining agreement) using procedures such as text searches for relevant keywords in the job-level data, which can be error-prone. After 2002, the pay-setting mechanism was explicitly coded in the dataset and therefore measured with less error. [9]
Clustering standard errors at the individual job level produced standard errors that were more conservative than clustering at the wage group level. [10]
These estimates are slightly higher than those found for the United States. For example, Neumark, Schweitzer and Wascher (2004) estimate that the short-run elasticity of minimum-wage workers' hourly wages with respect to the US minimum wage is 0.8. [11]
Due to a number of extreme values for log changes in average hours worked, I exclude any jobs with a log change greater than 4 standard deviations away from the sample mean. My estimates are not sensitive to this decision. [12]
Although these estimates do not capture any effect of award wage changes on overtime hours worked (since the hours worked variable only includes ordinary-time hours), I also find no effect of award wage changes on the probability that the job occupant worked any paid overtime hours during the survey period. This is modelled using a binary dependent variable that equals one if the occupant of the job received an overtime payment in the last full pay period prior to the WPI survey date, and zero otherwise (conditional on the job being active in the quarter). [13]
I exclude any jobs whose EBA includes an automatic adjustment to FWC decisions, because such EBAs are not a valid control group. I am able to identify such agreements in the data since the WPI survey collects information on the source(s) of any change in wages between consecutive quarterly surveys. I exclude from the EBA sample any job that ever listed an FWC decision as a reason for a pay adjustment. This comprises around one-fifth of all EBA jobs in the survey. [14]
Prior to the WorkChoices legislation, employees were covered by a patchwork of federal and state awards. For essentially historic reasons, some jobs were covered by federal awards, while others were subject to state awards (Stewart 2015, p 7). In practice, however, prior to 2006 the state industrial relations commissions had almost always announced the same increases as that announced by the federal commission, albeit with a lag of several months. [15]
In its most recent review of award wages, the FWC (2017) cited international research that ‘modest and regular’ wage increases do not result in an increase in unemployment. [16]