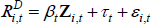RDP 2018-05: Do Interest Rates Affect Business Investment? Evidence from Australian Company-level Data 4. Accounting for Sample Selection
April 2018
- Download the Paper 1,258KB
Our estimates of the sensitivity (or ‘elasticity’) of company investment with respect to the cost of debt may be affected by sample selection bias. Interest rate data are only observable for companies with debt; therefore, we can only estimate the elasticity for these companies. If companies without debt have a different elasticity, our estimates will be biased.
It is difficult to assess the size and direction of this bias. We could be overestimating the size of the negative relationship between interest rates and investment if companies with debt are relatively more sensitive to interest rates. This might be the case if, for instance, companies that have outstanding floating-rate debt receive higher cash flows when rates fall, which could stimulate investment if they are financially constrained (e.g. Ippolito, Ozdagli and Perez-Orive 2017). Companies without debt would not be affected by this cash flow channel, and so would be less sensitive to interest rate changes. Alternatively, we could be underestimating the negative relationship between interest rates and investment if companies without debt are more sensitive to interest rates. This might happen if there are companies that have no debt because they are borrowing constrained, and for whom the constraint would be relaxed if rates fell and made serviceability more feasible.[21] A slight fall in rates would lead to a large increase in borrowing and investment by these companies.
The standard approach to dealing with sample selection bias is to use a sample selection model, such as the Heckman (1979) approach, or an endogenous switching model (e.g. Lee 1978; Hu and Schiantarelli 1998). These approaches formally model the selection mechanism alongside the equation of interest. However, they are designed for cases where we are missing data on the dependent variable – investment – rather than on the explanatory variable – the interest rate – as these approaches generally include the explanatory variable in the selection model.
Instead, we employ multiple imputation (MI), a technique pioneered in Rubin (1987).[22] The idea behind MI is to impute reasonable values for the missing variables using the observed data and an imputation model. The imputed values can be used to complete the sample. The relationships of interest can then be estimated using the completed sample. Rather than doing this once, we do it multiple (m) times, and each time we add some random variation to the imputed variables. This allows us to account for noise and uncertainty in the imputation process. The coefficients of interest are taken as the average coefficient across the m estimations. The standard errors can be computed based on the variance of the coefficients within and between the m estimations.
For this approach to be valid, we need to assume that the data are ‘missing at random’ (MAR). That is, conditional on all of the other variables, the fact that the data are missing provides no additional information. To make this more concrete, in our case MAR requires that the missing nature of the interest rate data is not a signal that it is high (or low), once we take account of all of the information contained in the variables we have used to impute the interest rate. Put another way, the true missing observation should be equal to the imputed value plus a white noise error term.
In reality, this is likely to be a strong assumption. Under our maintained hypothesis, as interest rates increase, all else equal, companies are less likely to borrow, and so are more likely to be missing data. Our imputed interest rates are therefore likely to be lower compared to the true data. This ‘level’ effect can be dealt with relatively easily using company fixed effects.
More concerning is the possibility that the error is not white noise, and might be systematically related to investment. For instance, even if our imputation model is good, unobserved credit supply shocks will create a wedge between the imputed and true interest rate values. Therefore, the imputed interest rate variable will include an error that, under the maintained hypothesis, is positively correlated with investment. This means that our estimated coefficient is likely to be biased upwards.[23] Still, this at least allows us to say something about the likely direction of the bias, which we cannot do with the estimates from Section 3.2.1.
4.1 Model and Results
As noted above, to use MI we need to specify a model for imputation. We model interest rates as:
where Zi,t is a vector of variables taken from the company's balance sheet that may be related to the company's riskiness, demand for credit, and interest rates more generally.[24]
Table 3 contains the results from the MI estimation. The estimated coefficients on the cost of debt are negative, but are insignificant and are somewhat closer to zero than those we obtain when estimating the model using only companies with debt. This suggests that the companies without debt may have less interest-sensitive investment, compared to companies with debt. If this is the case, care needs to be taken in extrapolating results from regressions using only companies with debt to the whole universe of firms.
There are some caveats to this finding. First, as discussed above, the estimates are likely to be biased upwards. Therefore we cannot conclusively contend that the companies without debt have a lower elasticity of investment with respect to debt. Second, even if bias is not an issue, it is possible that the differences in elasticities could reflect our focus on tangible investment. In our sample, companies without debt appear to invest more heavily in intangible assets. This is consistent with the fact that many debt-free companies are in the healthcare and information technology sectors. As such, their tangible investment elasticity could be lower, but their total investment elasticity may not be.
Still, the potential for different elasticities of investment has important implications for understanding the pass-through of monetary policy and of shocks to the financial sector. As such, it would be worthwhile further interrogating the results in future work using other data sources or techniques.
| Net investment | Gross investment | |
|---|---|---|
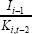 |
0.06* (0.03) |
−0.60** (0.05) |
| ki,t−2 | 0.04 (0.21) |
−1.58* (0.95) |
| Cost of debt | ||
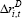 |
−0.22 (0.20) |
−0.20 (0.44) |
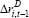 |
−0.20 (0.36) |
−0.35 (0.74) |
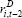 |
−0.38 (0.55) |
−0.83 (1.07) |
| Sales | ||
| Δyi,t | 0.20*** (0.05) |
−0.40 (0.48) |
| Δyi,t−1 | −0.07 (0.14) |
−0.83 (0.79) |
| yi,t−2 | −0.22 (0.22) |
0.11 (0.26) |
| Observations | 427 | 444 |
|
Notes: *, **, *** indicate significance at the 10, 5 and 1 per cent levels, respectively; standard errors are reported in parentheses |
||
Footnotes
This might happen if, for example, there is some fixed cost in making initial debt offerings, or in forming a relationship with a bank and getting an initial loan. [21]
For an overview of MI as well as other methods to deal with missing data, see Enders (2010). [22]
To get around this issue most of the literature recommends including the outcome variable in the imputation equation. This would seem to lead to ‘self-fulfilling prophecies’ where we find a relationship between the imputed and outcome variables by construction, but a number of papers have shown that this is not the case (e.g. Moons et al 2006). However, our study differs somewhat from most of the literature in that we are specifically concerned that those companies with missing data may have a different relationship between the explanatory variable and the outcome variable. [23]
For more details on the actual estimation, see Appendix C. [24]