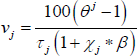RDP 2018-04: DSGE Reno: Adding a Housing Block to a Small Open Economy Model 3. Estimation
April 2018
- Download the Paper 1,668KB
We take the model to the data using a mix of calibration and estimation. As shown by Komunjer and Ng (2011), not all parameters of medium- and large-scale DSGE models are identified. Therefore, some parameters must be calibrated. We choose to calibrate parameters in the model that are known to be weakly identified in the literature and those which are most important for determining the steady state of the model. We calibrate these parameters to roughly match some key aggregate values, such as: the investment, consumption, import and export shares of GDP; and the housing share of the total capital stock. We estimate the remaining parameters, which mostly govern the dynamic predictions of the model, using standard Bayesian techniques. These include the exogenous shock processes, Phillips curve relationships, monetary policy parameters, and their counterparts in the world economy. Below, we provide a description of the data and the calibrated and estimated parameters.
We take a first-order approximation of the households' and firms' first-order conditions, and the capital accumulation equations around their respective steady states. We then use the software package Dynare to solve for the rational expectations solution of the model and to estimate parameters.
3.1 Data
We estimate the model using 26 macroeconomic data series. Of these, 22 series are Australia-specific, while the remaining ones capture movements in the world economy. The series and their sources are reported in Appendix A. To capture the housing sector, we consider four measures of activity: housing sector value added; the housing-related components of the CPI; a housing sector wage index; and housing investment. We use data from the March quarter of 1992 to the December quarter of 2016 for all series but the wage price indices, which are only available starting in the December quarter of 1997. We supplement these data with information on import volumes, public demand and capital stocks to calibrate the steady state of the model.
The world economy is summarised by major trading partner (MTP) GDP growth, the trade-weighted MTP inflation rate, the average interest rate in the G3 (United States, euro area, and Japan), and price growth in world commodity prices. The world economy is assumed to be exogenous to Australia and is estimated separately as in Kulish and Rees (2011). The Australian economy is summarised by standard aggregate variables such as GDP growth, consumption growth, CPI inflation and the cash rate, as well as several sector-specific growth and inflation measures.
3.2 Calibrated Parameters
Table 1 shows the values chosen for the calibrated parameters of the model. The key calibrated parameters are labour-augmented productivity growth, the discount factor, parameters of the various sector production functions, the elasticities of substitution between goods, and the consumption shares of the different sectors. These parameter choices follow RSH where possible. The production function parameters are chosen to reflect sectoral income shares observed in the data. We make some minor adjustments to the parameters to hit the steady-state targets.[13]
| Parameter | Description | Value |
|---|---|---|
| Technology and policy | ||
| μ | Steady-state labour-augmenting productivity growth | 1.008 |
| π | Steady-state inflation rate | 1.0062 |
| π* | Steady-state foreign inflation rate | 1.005 |
| ι | Risk premium scale parameter | 0.0001 |
| b* | Controls steady-state trade deficit | 0.25 |
| g | Controls share of public demand in GDP | 0.6487 |
| Households | ||
| β | Households' discount factor | 0.9996 |
| ωn | Controls share of non-tradeables in domestic final demand | 0.3970 |
| ωm | Controls share of non-resource tradeables in domestic final demand | 0.1118 |
| ωd | Controls share of housing in domestic final demand | 0.2447 |
| ωf | Controls share of imports in domestic final demand | 0.2465 |
| ζ | Intersectoral elasticity of substitution in domestic final demand | 0.8 |
| ξ | Elasticity of substitution between domestic and foreign goods overseas | 0.8 |
| η | Labour elasticity | 1 |
| σ | Intersectoral labour supply elasticity | 1 |
| AH | Normalising constant for labour in the utility function | 4.4177 |
| Ad | Normalising constant for capital in the utility function | 0.3 |
| Non-tradeable sector | ||
| αn | Labour share | 0.71 |
| γn | Capital share | 0.24 |
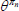 |
Elasticity of substitution between differentiated goods | 6 |
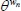 |
Elasticity of substitution between differentiated labour | 0.25 |
| δn | Depreciation rate | 0.0047 |
| Φn | Investment adjustment cost parameter | 20 |
| Non-resource tradeable sector | ||
| αm | Labour share | 0.62 |
| γm | Capital share | 0.32 |
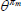 |
Elasticity of substitution between differentiated goods | 6 |
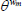 |
Elasticity of substitution between differentiated labour | 0.25 |
| δm | Depreciation rate | 0.0075 |
| Φm | Investment adjustment cost parameter | 20 |
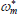 |
Controls share of non-resource tradeables that are exported | 0.6541 |
| Resource sector | ||
| αz | Labour share | 0.2 |
| αL,z | Land share | 0.5 |
| δz | Depreciation rate | 0.007 |
| Φz | Investment adjustment cost parameter | 20 |
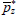 |
Steady-state foreign-denominated resource price | 1 |
| Housing sector | ||
| αd | Labour share | 0.32 |
| γd | Capital share | 0.64 |
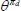 |
Elasticity of substitution between differentiated goods | 6 |
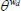 |
Elasticity of substitution between differentiated labour | 0.25 |
| δd | Depreciation rate | 0.0023 |
| Import sector | ||
| θf | Elasticity of substitution between differentiated goods | 6 |
Table 2 shows the steady-state targets and the model-implied values given the chosen parameters. The model matches the data reasonably well. It does a particularly good job of matching the housing-related quantities, especially the housing capital stock's average proportion of the overall capital stock. Therefore, we believe the parameterisation chosen is appropriate moving forward. To reiterate the role that our preference specification plays, if the assumption that the housing stock is in the utility function is removed, but the same calibration is used, the housing share of the capital stock falls by around 10 percentage points.
We also make one calibration choice based on the dynamic predictions of the model. We calibrate the sectoral investment adjustment costs for the non-tradeable, tradeable, and resource sectors. Investment adjustment costs play a significant role in determining the response of sectoral investment to a monetary policy shock. Because only aggregate investment and housing investment are observable, the investment responses in the remaining sectors are not well-identified. Therefore, we calibrate investment adjustment costs to be relatively large in these sectors so that the model predicts more muted responses. As we show in Section 4.2, this is consistent with evidence based on a VAR model.
| Variable | Average 1993–2016 | Model prediction |
|---|---|---|
| Expenditure as a share of GDP | ||
| Consumption | 56.9 | 55.8 |
| Private investment | 21.3 | 22.5 |
| Public demand | 22.7 | 22.5 |
| Production as a share of nominal GVA(a) | ||
| Non-tradeable | 47.5 | 46.2 |
| Tradeable | 25.3 | 24.2 |
| Resource | 12.3 | 11.6 |
| Housing | 15.7 | 18.0 |
| Trade | ||
| Import share of GDP | 20.6 | 20.6 |
| Export share of GDP | 19.5 | 19.6 |
| Resource share of export value | 43.4 | 37.2 |
| Investment as a share of total investment(a) | ||
| Non-tradeable | 29.8 | 33.4 |
| Tradeable | 23.0 | 23.8 |
| Resource | 17.1 | 15.1 |
| Housing | 30.0 | 27.6 |
| Capital stock | ||
| Housing share of capital stock | 37.6 | 34.1 |
|
Note: (a) Based on broad definition of resource sector discussed in Rayner and Bishop (2013) |
||
Finally, we include a number of calibrated reconciliation/measurement error terms. Because we use chain volume measures for GDP growth and for the growth in value added in each of the intermediate sectors, these components are additive in levels in the model but are not additive in the data. Similarly, we use trimmed mean CPI inflation, but headline measures of sectoral inflation. Therefore, to account for these and any other differences between the data and their model counterparts, we include a white noise measurement error term for each observable series, apart from: the nominal and real exchange rates; commodity prices; domestic interest rates; and foreign and domestic aggregate inflation and GDP.[14] The errors are calibrated to be 10 per cent of the observed variance in the variable. We do not impose any structure on the correlation of these reconciliation shocks with one another.[15]
3.3 Estimated Parameters
We estimate the model using Bayesian techniques. We choose informative prior distributions for each of the model parameters of interest and use the Metropolis-Hastings algorithm to take draws from the implied joint posterior distributions. We follow RSH and Kulish and Rees (2011) and estimate the model in two stages. First, we estimate the world economy's structural parameters separately. We then take these parameters as given in the second stage, when estimating the structural parameters of the small open economy and the parameters of the exogenous shock processes.[16] For estimation, we take 100,000 draws of the posterior distribution and discard the first 20,000. We run multiple chains and assess convergence using Brooks and Gelman (1998) method included in Dynare.[17]
Table 3 shows the estimated parameter values for the world economy obtained in the first stage of estimation. The parameter estimates are in line with those obtained in the existing literature for estimation on US data, such as An and Schorfheide (2007) or Smets and Wouters (2007). In particular, the Taylor-rule coefficients fall within standard ranges found in the literature, with monetary policy responding aggressively to deviations of inflation from target and a much smaller response to changes in real output growth. In addition, the world Phillips curve is estimated to be relatively flat and output shocks tend to be much larger than inflation shocks.
| Parameter | Prior distributions | Posterior distributions | ||||||
|---|---|---|---|---|---|---|---|---|
| Shape | Mean | Std dev | Mode | Mean | 5th percentile | 95th percentile | ||
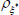 |
Beta | 0.50 | 0.15 | 0.94 | 0.94 | 0.91 | 0.97 | |
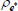 |
Beta | 0.50 | 0.15 | 0.55 | 0.53 | 0.34 | 0.71 | |
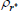 |
Beta | 0.75 | 0.10 | 0.83 | 0.82 | 0.77 | 0.87 | |
| ρμ | Beta | 0.40 | 0.20 | 0.30 | 0.33 | 0.05 | 0.61 | |
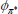 |
Normal | 1.50 | 0.20 | 1.37 | 1.41 | 1.17 | 1.63 | |
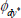 |
Normal | 0.13 | 0.05 | 0.23 | 0.23 | 0.15 | 0.30 | |
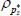 |
Beta | 0.50 | 0.15 | 0.94 | 0.94 | 0.91 | 0.97 | |
| θzy | Normal | 0.00 | 0.20 | 0.12 | 0.12 | −0.19 | 0.46 | |
| χ* | Beta | 0.30 | 0.15 | 0.23 | 0.27 | 0.09 | 0.46 | |
| κ* | Gamma | 1.00 | 0.80 | 0.97 | 1.52 | 0.42 | 2.63 | |
| Standard deviations (× 100) | ||||||||
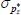 |
Gamma | 0.50 | 0.40 | 6.22 | 6.31 | 5.59 | 7.04 | |
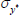 |
Gamma | 0.50 | 0.40 | 0.97 | 1.00 | 0.73 | 1.30 | |
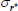 |
Gamma | 0.50 | 0.40 | 0.08 | 0.08 | 0.06 | 0.10 | |
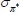 |
Gamma | 0.50 | 0.40 | 0.06 | 0.06 | 0.05 | 0.08 | |
| σμ | Gamma | 0.50 | 0.40 | 0.06 | 0.13 | 0.01 | 0.24 | |
Tables 4 and 5 show the estimated parameter values for the Australian economy. The estimates of the monetary policy rule are similar to those for the world economy, and those from RSH. Australian monetary policy responds aggressively to deviations in inflation from target and less so to changes in real output. Consistent with RSH, there is no evidence that monetary policy responds to changes in the real exchange rate. There is evidence of habit persistence in both the consumption of goods and in the holding of housing. The persistence in consumption is much larger than that associated with the holding of the housing capital stock. In part, this reflects the prior we impose, which implies that households are more willing to adjust their holdings of the physical housing stock than their consumption of the services it provides. We have a low prior value in this case because we also assume capital adjustment costs, so households already face frictions in adjusting the capital stock.
As in RSH, rather than estimating the price adjustment costs, about which we have no strong prior beliefs, we directly estimate the slopes of the Phillips curves. Each slope is just a monotonic transformation of the adjustment cost parameters. Specifically:
for 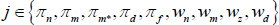 .
.
We, however, use different priors to those used in RSH. We use priors based on micro evidence from Sutton (2017). The estimated slopes reveal much flatter Phillips curve relationships in the housing and non-tradeable sectors than in the non-resource tradeable sector, while the degree of indexation to lagged inflation in these two sectors is higher. In terms of the model, this is consistent with a higher cost to adjusting prices and a higher dependence on recent conditions in these two sectors. We apply the same estimation strategy to the wage Phillips curves, though we use uninformative priors. The slopes of the wage Phillips curves are roughly the same across the sectors and are relatively flat in all cases. The degree of indexation is also similar across industries, revealing no significant differences in wage setting across the intermediate industries.
Finally, the estimated shock processes all exhibit moderate to high persistence. This is due to the fact that DSGE models under rational expectations lack significant propagation mechanisms for shocks. Therefore, to explain the persistence observed in data, the shock processes must be highly persistent. There are also a few persistence parameters that appear not to be well-identified. For example, the data does not add much to the priors on the autoregressive coefficient on either the housing stock preference shock or the labour supply shock.
| Parameter | Prior distributions | Posterior distributions | ||||||
|---|---|---|---|---|---|---|---|---|
| Shape | Mean | Std dev | Mode | Mean | 5th percentile | 95th percentile | ||
| Habit persistence and investment adjustment costs | ||||||||
| b | Beta | 0.50 | 0.20 | 0.90 | 0.90 | 0.85 | 0.94 | |
| bd | Beta | 0.20 | 0.10 | 0.16 | 0.21 | 0.04 | 0.36 | |
| Φd | Normal | 3.00 | 1.50 | 3.74 | 4.03 | 2.71 | 5.42 | |
| Monetary policy and UIP | ||||||||
| ρr | Beta | 0.90 | 0.03 | 0.87 | 0.87 | 0.84 | 0.89 | |
| ϕπ | Normal | 1.50 | 0.10 | 1.54 | 1.55 | 1.40 | 1.70 | |
| ϕdy | Normal | 0.20 | 0.03 | 0.21 | 0.21 | 0.17 | 0.25 | |
| ϕq | Normal | 0.00 | 0.05 | 0.00 | −0.01 | −0.04 | 0.03 | |
| Θψ | Beta | 0.50 | 0.15 | 0.07 | 0.08 | 0.03 | 0.13 | |
| Price and wage Phillips curves | ||||||||
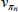 |
Gamma | 8.00 | 2.00 | 2.93 | 3.54 | 1.94 | 5.08 | |
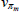 |
Gamma | 10.00 | 2.50 | 9.16 | 9.30 | 5.50 | 12.95 | |
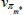 |
Gamma | 10.00 | 2.50 | 4.74 | 5.26 | 3.19 | 7.35 | |
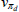 |
Gamma | 1.00 | 0.30 | 0.12 | 0.15 | 0.09 | 0.22 | |
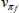 |
Gamma | 10.00 | 2.50 | 2.03 | 2.21 | 1.46 | 2.99 | |
| χn | Beta | 0.30 | 0.15 | 0.29 | 0.30 | 0.11 | 0.47 | |
| χm | Beta | 0.30 | 0.15 | 0.17 | 0.21 | 0.04 | 0.37 | |
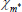 |
Beta | 0.30 | 0.15 | 0.08 | 0.12 | 0.02 | 0.22 | |
| χd | Beta | 0.30 | 0.15 | 0.63 | 0.62 | 0.45 | 0.79 | |
| χf | Beta | 0.30 | 0.15 | 0.15 | 0.17 | 0.05 | 0.30 | |
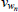 |
Gamma | 50 | 30 | 0.13 | 0.19 | 0.09 | 0.29 | |
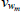 |
Gamma | 50 | 30 | 0.10 | 0.14 | 0.06 | 0.21 | |
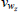 |
Gamma | 50 | 30 | 0.12 | 0.13 | 0.07 | 0.20 | |
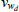 |
Gamma | 50 | 30 | 0.15 | 0.19 | 0.10 | 0.27 | |
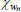 |
Beta | 0.30 | 0.15 | 0.12 | 0.16 | 0.02 | 0.29 | |
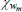 |
Beta | 0.30 | 0.15 | 0.20 | 0.25 | 0.10 | 0.39 | |
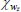 |
Beta | 0.30 | 0.15 | 0.26 | 0.29 | 0.11 | 0.47 | |
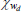 |
Beta | 0.30 | 0.15 | 0.10 | 0.13 | 0.03 | 0.22 | |
| Shock persistence | ||||||||
| ρg | Beta | 0.50 | 0.20 | 0.75 | 0.66 | 0.38 | 0.91 | |
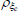 |
Beta | 0.50 | 0.20 | 0.54 | 0.54 | 0.36 | 0.72 | |
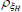 |
Beta | 0.50 | 0.20 | 0.93 | 0.91 | 0.86 | 0.96 | |
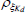 |
Beta | 0.50 | 0.20 | 0.50 | 0.51 | 0.17 | 0.85 | |
| ρϒ | Beta | 0.50 | 0.20 | 0.67 | 0.63 | 0.51 | 0.75 | |
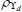 |
Beta | 0.50 | 0.20 | 0.62 | 0.59 | 0.45 | 0.74 | |
| ρψ | Beta | 0.50 | 0.08 | 0.78 | 0.77 | 0.73 | 0.82 | |
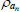 |
Beta | 0.50 | 0.20 | 0.75 | 0.72 | 0.63 | 0.83 | |
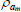 |
Beta | 0.50 | 0.20 | 0.98 | 0.96 | 0.92 | 1.00 | |
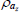 |
Beta | 0.50 | 0.20 | 0.93 | 0.91 | 0.85 | 0.97 | |
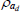 |
Beta | 0.50 | 0.20 | 0.75 | 0.71 | 0.62 | 0.81 | |
| Parameter | Prior distributions | Posterior distributions | ||||||
|---|---|---|---|---|---|---|---|---|
| Shape | Mean | Std dev | Mode | Mean | 5th percentile | 95th percentile | ||
| Policy and preferences (× 100) | ||||||||
| σg | Gamma | 1.00 | 0.80 | 1.23 | 1.22 | 0.99 | 1.40 | |
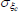 |
Gamma | 1.00 | 0.80 | 4.49 | 4.54 | 2.89 | 6.15 | |
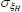 |
Gamma | 1.00 | 0.80 | 5.97 | 5.82 | 3.38 | 8.23 | |
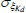 |
Gamma | 1.00 | 0.80 | 0.36 | 0.86 | 0.03 | 1.68 | |
| σr | Gamma | 0.15 | 0.10 | 0.11 | 0.11 | 0.10 | 0.13 | |
| σψ | Gamma | 0.50 | 0.40 | 0.92 | 0.99 | 0.75 | 1.23 | |
| Production (× 100) | ||||||||
| σϒ | Gamma | 2.00 | 1.50 | 24.01 | 26.18 | 19.71 | 31.80 | |
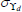 |
Gamma | 2.00 | 1.50 | 7.31 | 8.23 | 4.79 | 11.59 | |
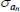 |
Gamma | 1.00 | 0.80 | 1.42 | 1.43 | 1.23 | 1.61 | |
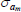 |
Gamma | 1.00 | 0.80 | 0.57 | 0.67 | 0.41 | 0.93 | |
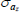 |
Gamma | 1.00 | 0.80 | 1.85 | 1.88 | 1.65 | 2.13 | |
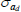 |
Gamma | 1.00 | 0.80 | 3.76 | 3.78 | 3.26 | 4.31 | |
| Price and wage inflation (× 100) | ||||||||
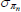 |
Gamma | 0.50 | 0.40 | 0.35 | 0.36 | 0.30 | 0.43 | |
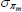 |
Gamma | 0.50 | 0.40 | 0.54 | 0.54 | 0.45 | 0.63 | |
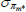 |
Gamma | 0.50 | 0.40 | 2.59 | 2.68 | 2.23 | 3.07 | |
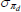 |
Gamma | 0.50 | 0.40 | 0.18 | 0.19 | 0.15 | 0.22 | |
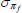 |
Gamma | 0.50 | 0.40 | 1.00 | 1.02 | 0.86 | 1.20 | |
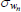 |
Gamma | 0.15 | 0.10 | 0.05 | 0.05 | 0.02 | 0.07 | |
 |
Gamma | 0.15 | 0.10 | 0.10 | 0.10 | 0.08 | 0.12 | |
 |
Gamma | 0.15 | 0.10 | 0.19 | 0.19 | 0.15 | 0.24 | |
 |
Gamma | 0.15 | 0.10 | 0.21 | 0.22 | 0.18 | 0.25 | |
3.4 Forecast Performance
In this section, we assess the out-of-sample forecasting performance of the model. The DSGE model is not designed for forecasting. However, its pseudo out-of-sample forecast performance can be used to assess the model's ability to capture sectoral dynamics, in particular those related to the housing sector. Put another way, we can use the forecast performance as a goodness of fit measure.
In our forecasting exercise, we produce out-of-sample forecasts for a number of variables for horizons of 1 to 10 quarters ahead. We use a recursive strategy, extending the sample by 1 quarter at a time before producing each set of forecasts. Our first set of forecasts use data up to June 2002, and our last set of forecasts use data up to June 2014. Forecasts are then compared to the actual outcomes, and the errors are used to calculate root mean squared forecast errors (RMSFE) for each variable at each horizon.
Rather than re-estimating the model parameters with each new observation, we only update the parameters after an additional year of data (equivalent to four observations) becomes available. In addition to reducing computational time, this reflects more accurately the frequency with which DSGE models are typically re-estimated at the Bank.
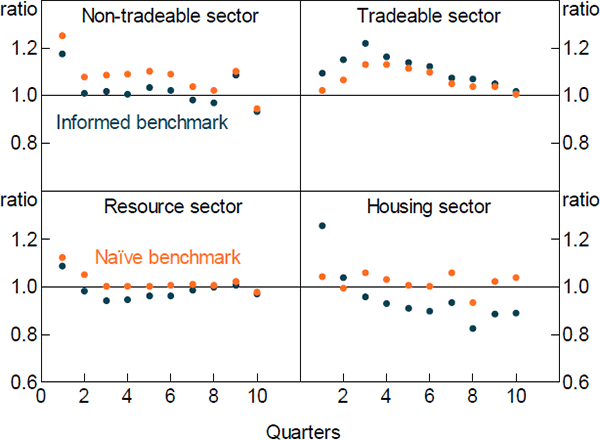
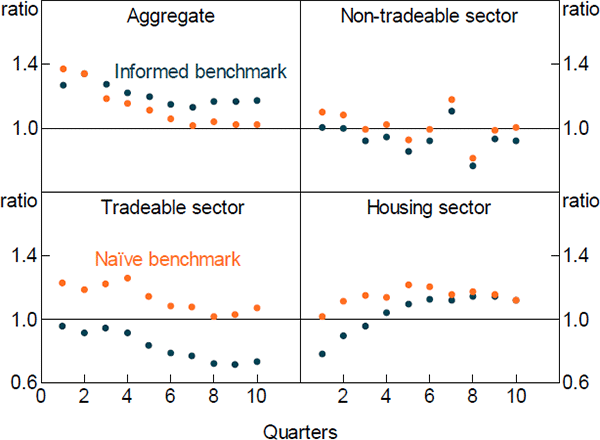
We compare the DSGE model's RMSFE to two simple benchmarks. The first is the standard deviation of the actual outcomes over the full sample. This is equivalent to comparing the DSGE model's RMSFE to that of an ‘informed’ model, which forecasts the variables to be equal to their full sample means. As the full sample mean is not available to the DSGE model when it produces its forecasts, this represents a relatively high bar.[18] The second benchmark is the RMSFE from a ‘naïve’ model. We use an autoregressive model of order one (AR1) for each variable. Again, this is a reasonably high bar as it is generally quite difficult to forecast more accurately than an AR1 model. All variables considered are quarterly growth rates.
Figures 6 and 7 show the relative forecast performance of the DSGE model for GDP and its components. The DSGE model produces forecasts that are broadly comparable in terms of accuracy to those from an AR1 model at most forecast horizons, though its medium-term GDP forecasts are somewhat less accurate. It also performs favourably compared to the informed benchmark, particularly for housing sector value added, and housing and total investment. Figure 8 shows the relative forecast performance for inflation and its components. The DSGE model does not forecast aggregate inflation particularly well. This reflects the fact that it forecasts imported inflation poorly. In contrast, it does a reasonable job in forecasting the domestic components of inflation, particularly at longer horizons.
Overall, our model produces forecasts that are broadly comparable to both informed and naïve benchmarks. Its forecasts for housing sector variables are particularly good. This is reassuring, as it suggests that the DSGE model is adequately capturing housing sector dynamics, which is the intent of this paper.
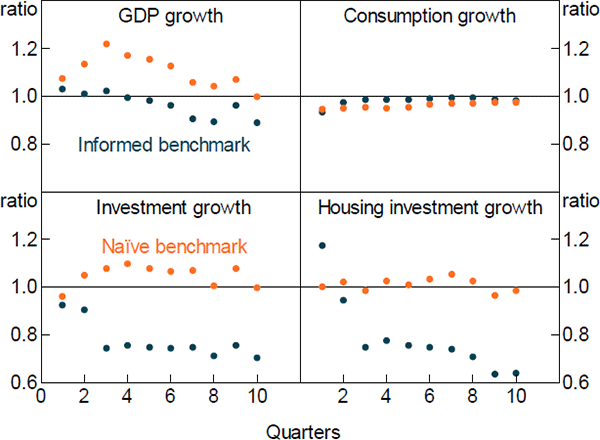
Note: Ratio of DSGE model RMSFE to benchmark model RMSFE
Note: Ratio of DSGE model RMSFE to benchmark model RMSFE
Note: Ratio of DSGE model RMSFE to benchmark model RMSFE
Footnotes
Unless otherwise noted, we use the same calibrated parameters in the foreign economy as in the domestic economy. For example, the discount rate β is set to the same value in both economies. [13]
As we include errors in the inflation and GDP components, we do not also include them in the aggregates. [14]
We have tried a number of different measurement error specifications, including moving average unit root processes for key aggregate and foreign variables, white noise errors included on all observables, and the removal of all such error terms from the model. We find that, at a minimum, some error terms must be included in the sector-specific level variables in order for the model to be estimated. This is due to the non-additivity of chain volume measures and definitional incongruences between sectoral observables and their model counterparts. However, we find that the precise specification of these terms does not have a significant impact on the inference of estimated parameters once some error is included at the sectoral level. Therefore, we chose the most parsimonious specification. [15]
We set the world economy parameters to the mean values of the posterior distribution. [16]
Graphical evidence suggests the number of draws is sufficient to ensure convergence. We obtain an acceptance rate of about 30 per cent. [17]
Since the model calibrations and assumed priors are based on the full sample, the DSGE model is not at a complete informational disadvantage. [18]