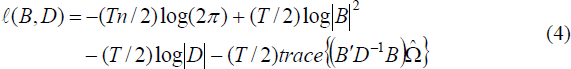RDP 2008-01: A Sectoral Model of the Australian Economy 2. Methodology

We use an SVAR to estimate the effect of monetary policy on the different sectors of the economy. SVARs are a straightforward way of capturing important macroeconomic relationships without using a large number of variables or imposing restrictive assumptions on the model. Also, they are commonly used in the literature, allowing us to compare our results with those of other studies.

We assume that the economy can be represented by the following structural form:

where 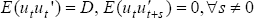, B is a non-singular matrix that is normalised to have 1s on the diagonal, X_t is an n × 1 vector of macroeconomic variables, C(L) is a polynomial in the lag operator L, and u_t is an n × 1 vector of structural disturbances. The matrix B summarises the contemporaneous relationship between the endogenous variables, while C(L) summarises how the variables are affected by their own lags as well as the lags of the other variables in the system. The u_t are serially uncorrelated and D is a diagonal matrix whose off-diagonal elements are zero and whose diagonal elements are the variances of structural disturbances.

Because X_t is endogenous, direct estimation of Equation (1) by OLS produces biased and inconsistent estimates. Thus, to recover consistent maximum likelihood estimates of B and D, we must first estimate the reduced-form model:

where .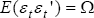

The structural disturbances and the reduced-form residuals are related by u_t = Bε_t, which implies that:

From Equation (3), we can recover B and D if sufficient restrictions are imposed on the two matrices. Because Ω is a symmetric matrix, there are only (n² + 1) / 2 free parameters, so at least (n² − 1) / 2 restrictions need to be imposed.

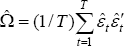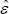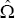A simple two-step maximum likelihood estimation procedure can be employed to recover the structural parameters, assuming that the structural errors are jointly normal. First, Ω is estimated as , where are the OLS residuals from each equation of the reduced-form model. Estimates of B and D are then obtained by maximising the following log-likelihood for the system conditional on : ^[1]

A typical way of recovering the structural parameters in an SVAR is to restrict some of B's off-diagonal elements to be zero. A popular method is to orthogonalise the reduced-form disturbances by Cholesky decomposition, implying a recursive temporal ordering of the variables. An alternative, followed here, is to adopt a set of restrictions informed by economic theory (Bernanke 1986; Sims 1986). Neither approach is without its critics.^[2] Cooley and Leroy (1995) point out that recursive models have become less popular over time because of the difficulty in finding a theoretically valid causal structure, while others have argued that the results from non-recursive models can be highly sensitive to small changes in the identifying restrictions (Faust 1998). We deal with this issue by employing a range of plausible identifying restrictions to gauge how robust our results are to such changes.

Footnotes

The maximum likelihood estimates were obtained using Chris Sims' ‘csminwel’ program. [1]

An alternative literature identifies SVARs via restrictions on the long-run relationships between variables (Blanchard and Quah 1989) or restrictions on both contemporaneous and long-run relationships (Galí 1992). [2]