RBA Annual Conference – 2012 Taming the Real Estate Beast: The Effects of Monetary and Macroprudential Policies on Housing Prices and Credit Kenneth Kuttner and Ilhyock Shim[*]
1. Introduction
Recent events have underscored the importance of asset price booms and busts as sources of financial instability. Unsustainable property price appreciation figured prominently in the 2007–2009 financial crisis, in the 1997–1998 Asian financial crisis, and in Japan's property market collapse in the early 1990s. Monetary policy has come under intense scrutiny as a possible factor contributing to the escalation in real estate prices, with some blaming the US Federal Reserve's low interest rate policy for creating a bubble in the US housing market.
These tumultuous experiences have generated a great deal of interest in two interrelated questions. The first is the extent to which housing price and credit movements are explained by changes in interest rates and, by extension, whether monetary policy would be effective in attenuating housing market excesses. The second concerns the effectiveness of non-interest rate policies, such as prudential regulation, as additional tools for stabilising housing price and credit cycles. This is a crucial issue for central banks seeking to ensure financial stability while simultaneously using interest rate policy in the pursuit of macroeconomic objectives. And it is especially pressing for countries with fixed or heavily managed exchange rates, where there is limited scope for interest rate policy to address property market imbalances.
This paper empirically addresses both of these questions using data from 57 economies going back as far as 1980. The scope is therefore considerably broader than most existing work, such as Girouard et al (2006), which has mostly been limited to a smaller set of industrialised countries. We focus in particular on the Asia-Pacific region where non-interest rate policy measures have been used more actively than elsewhere.
Our investigation focuses on three classes of policy measures intended to affect housing prices and housing credit. The first consists of non-interest rate monetary policy actions, primarily changes in reserve requirements. The second category includes five distinct prudential policy measures: (i) maximum loan-to-value (LTV) ratios; (ii) maximum debt-service-to-income (DSTI) ratios; (iii) risk weights on mortgage loans; (iv) loan-loss provisioning rules; and (v) exposure limits to the property sector. The third category consists of fiscal policy measures such as capital gains tax at the time of sale of properties and stamp duties. One of the contributions of this paper is the compilation of an extensive dataset on the implementation of these macroprudential policies for a wide range of economies.[1]
We assess these policies' effects using panel regressions of housing price growth and housing credit growth, with models that also include controls for other factors affecting the housing market, such as rent, personal income and institutional features of the housing finance system. With regard to housing prices, our main findings are that increases in short-term interest rates and in the maximum LTV and/or DSTI ratios have strong, statistically significant effects. These results hold for several alternative model specifications, and in sub-samples that exclude the period affected by the financial crisis. Regarding the impact on housing credit, our results consistently show that limiting LTV and/or DSTI ratios and increasing loan-loss provisioning requirements tend to slow credit growth. Tax policies and exposure limits were also found to have the desired effects, although these results are sensitive to sample period and model specification. Taken together, our results suggest that macroprudential policies can be effective tools for stabilising housing price and credit cycles.
The plan of the paper is as follows. Section 2 surveys the existing evidence on the effects of monetary policy, financial structure and regulation. Section 3 outlines the standard theory of property prices, which will be used as a framework for understanding the potential roles of monetary policy, financial innovation and regulation in contributing to (or attenuating) property market fluctuations. Section 4 sketches the empirical approach. Section 5 describes the data used in the analysis, whose unique feature is an exhaustive compilation of a range of policy measures aimed at influencing conditions in the housing market. Section 6 reports the results, and Section 7 concludes.
2. Existing Evidence
Research on the effects of monetary and regulatory policies on the property market tends to fall into one of two categories. One strand of the literature, surveyed in Section 2.1, emphasises the effects of interest rates. The second strand focuses on macroprudential policies, often making use of cross-country or event-study methods. This literature is summarised in Section 2.2. The analysis in this paper combines elements of both.
2.1 The effects of interest rates
Many studies have documented the cyclical co-movement between interest rates and housing prices. Claessens, Kose and Terrones (2011), for example, show that housing prices are strongly procyclical in most countries. Ahearne et al (2005) find that low interest rates tend to precede housing price peaks, with a lead of approximately one to three years. While these patterns are suggestive, discerning the impact of interest rates per se is complicated by the fact that other macroeconomic factors affecting the demand for housing vary along with the interest rate. Moreover, it is impossible to tell from purely descriptive analysis whether the magnitude of the housing price variations are consistent with the effects implied by user cost theory.
Taking a more structured approach, Dokko et al (2009) use time series methods to construct housing price forecasts under alternative interest rate path assumptions in an effort to determine the extent to which low interest rates contributed to the housing price boom in the United States in the mid 2000s. They find that deviations from the Taylor rule explain only a small portion of the pre-crisis rise in property values, casting doubt on Taylor's (2007, 2009) assertion that overly expansionary monetary policy caused the boom.
A number of papers have used vector autoregressions (VARs) to gauge the impact of monetary policy shocks on housing prices. The four studies using this method summarised in Table 1 find a statistically significant impact of monetary policy on housing prices. Estimates of the maximum impact of a 25 basis point monetary policy shock on the level of housing prices range from 0.3 per cent to 0.9 per cent.[2] This is rather modest in economic terms, as it implies that a full percentage point contractionary shock would have reduced housing prices by less than 4 per cent. Table 1 also illustrates the sensitivity of the estimated dynamics to the identifying assumption: Del Negro and Otrok (2007) report a large contemporaneous response, while the other three papers' results suggest a more gradual adjustment process.
| Impact of a 25 basis point expansionary shock | |||
|---|---|---|---|
| Immediate | 10 quarters | Long run | |
|
Del Negro and Otrok (2007), Figure 5: United States, 1986–2005 |
0.9 | 0.2 | ≈ 0 |
| Goodhart and Hofmann (2008), Figure 3: 17 OECD countries, 1985–2006 |
0 | 0.4 | 0.8 |
| Jarociński and Smets (2008), Figure 4: United States, 1995–2007 |
0 | 0.5 | ≈ 0 |
| Sá, Towbin and Wieladek (2011), Figure 4: 18 OECD countries, 1984–2006 |
−0.1 | 0.3 | 0.1 |
An alternative approach to assessing interest rates' contribution to housing price fluctuations is derived from the user cost model. As discussed in Section 3, this model is based on a relationship linking the price of a property to the present value of future rents. One key implication of the model is that rents and property prices should be cointegrated, a possibility that has been investigated by Girouard et al (2006) for OECD countries, Mikhed and Zemčík (2007) for the Czech Republic, Gallin (2008) and Kuttner (2011) for the United States, Wu, Gyourko and Deng (2010) for China, and Glindro et al (2008) for Asia-Pacific economies.
The user cost approach also allows the variance in real estate prices to be decomposed into the contributions of fluctuations in interest rates, rents and an unobserved risk premium. Using the methodology developed in Campbell (1991), Campbell et al (2009) perform such a decomposition for housing prices in 23 metropolitan areas in the United States. They find that risk premia, rather than interest rates or rents, have been the principal source of variance in US housing prices.
Interestingly, the VAR estimates of interest rates' impact on property prices are considerably smaller than the effects implied by standard user cost theory sketched in Section 3. Specifically, the user cost model implies that for a plausible range of long-term interest rates, a 10 basis point decline in the long-term interest rate (a reduction that corresponds approximately to a 25 basis point expansionary monetary policy shock) would cause housing prices to rise by between 1.3 per cent to 1.6 per cent, far in excess of the 0.3 per cent to 0.9 per cent effect derived from VAR estimates.
2.2 The effects of financial structure and other policy measures
A few studies have looked at structural features as factors influencing the behaviour of housing prices. These include Iacoviello and Minetti (2003), which looks at financial liberalisation in Sweden, Finland and the United Kingdom; Calza, Monacelli and Stracca (2009), which considers the effects of institutional characteristics of national mortgage markets (such as mortgage equity withdrawal) and mortgage rate structure (fixed rate versus variable rate) in a group of advanced economies; and Glindro et al (2008), which investigates the implications of a range of structural features for housing price dynamics in Asia-Pacific economies. Moreover, Warnock and Warnock (2008, this volume) find that economies with stronger legal rights for borrowers and lenders, deeper credit information systems, easier property registration, and a more stable macroeconomic environment have deeper housing finance systems.
There is a growing literature documenting the use of macroprudential policy measures across countries and systematically examining the effectiveness of macroprudential policy measures on credit growth and housing prices. Before the recent financial crisis, Borio and Shim (2007) documented macroprudential and monetary policy measures taken by 18 economies to affect credit and housing prices. Using an event study methodology, they find that macroprudential measures reduced credit growth by 4 to 6 percentage points in the years immediately following their introduction, while housing prices decelerated in real terms by 3 to 5 percentage points. Hilbers et al (2005) focus on rapid growth of private sector credit in 18 central and eastern European (CEE) countries and document that 10 countries took measures in or before 2005.
More recently, Crowe et al (2011) select 36 economies which had experienced real estate booms and document that 24 had taken some policy measures. They provide a detailed discussion on the benefits and challenges associated with monetary, fiscal and macroprudential policy options. Using a dynamic stochastic general equilibrium model that includes a housing sector and credit markets, they show that tools that are narrower in focus and closer to the target, such as macroprudential measures, deliver the highest welfare. Also, Lim et al (2011) consider 49 economies which replied to an International Monetary Fund (IMF) survey conducted in December 2010, and document that 40 economies took macroprudential measures (broadly defined), including various prudential instruments, reserve requirements and limits on foreign currency lending. Using a panel regression analysis, they find that: (i) reserve requirements and dynamic provisioning have been effective in reducing real private sector credit growth during booms; (ii) reserve requirements have been effective in reducing leverage growth during booms; (iii) maximum LTV ratios, maximum DSTI ratios, dynamic provisioning and reserve requirements reduce the procyclicality of credit growth; and (iv) a maximum DSTI ratio, dynamic provisioning, countercyclical capital requirements, reserve requirements and limits on foreign currency lending reduce the procyclicality of leverage growth. It should be noted that Lim et al (2011) focus on the effectiveness of policy measures on private sector credit and leverage, while our paper focuses on the effectiveness of policy measures on housing credit and housing prices.
Finally, at the country level, there is a small number of studies that specifically analyse the effectiveness of macroprudential policies in Asia. For example, Wong et al (2011) show that reducing the maximum LTV ratio has had a significant dampening effect on real property price growth in Hong Kong SAR, while Igan and Kang (2011) find that capping LTV and DSTI ratios has reduced the rate of housing price appreciation in Korea.
3. Understanding What Drives Housing Prices
The purpose of this section is threefold. The first is to highlight the role of fundamentals in determining property values. The second is to provide a metric for assessing the economic and quantitative significance of empirical estimates of the impact of interest rates on property prices. The third is to understand the channels through which intermediation, innovation and regulation could affect property markets.
3.1 The user cost framework
A natural starting point for analysing the connection between interest rates and property prices is the venerable user cost model which, as argued by Himmelberg, Mayer and Sinai (2005), provides a useful benchmark for gauging the importance of economic fundamentals. The model is based on the simple proposition that market forces should equate the cost of renting with the all-in risk-adjusted cost of home ownership. The equality is expressed as:

where R/P is the rent-to-price ratio, i
is the relevant nominal interest rate, δ is the rate of physical
depreciation, σ is the risk premium associated with owning a
home, and 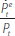 is expected nominal housing
price appreciation. The property and income tax rates, τp
and τy, also figure in the calculation, as in Poterba
(1984). Equivalently, subtracting and adding the expected rate of inflation
πe yields an expression in terms of the real interest
rate and the rate of real housing price appreciation:
is expected nominal housing
price appreciation. The property and income tax rates, τp
and τy, also figure in the calculation, as in Poterba
(1984). Equivalently, subtracting and adding the expected rate of inflation
πe yields an expression in terms of the real interest
rate and the rate of real housing price appreciation:
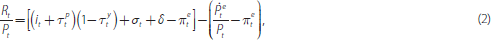
where the term in square brackets represents the real user cost, UC, excluding expected real house price appreciation.
The quantitative effects of interest rate changes on housing prices are easily calculated by differentiating Equation (2):

The expression shows that the effect, in percentage terms, of a 1 percentage point change in the interest rate depends on the user cost, which is in turn a function of i, δ, τp and τy and σ. An important implication is that the lower the user cost, the higher the sensitivity of the housing price to a given change in the interest rate. Starting from 7 per cent, for example, a 10 basis point reduction in the user cost would lead to an appreciation of approximately 1.4 per cent in the steady state. With the user cost initially at 5 per cent, the same 10 basis point reduction would lead to an appreciation of 2 per cent.
3.2 The role of financial intermediation
While useful for understanding the fundamentals underlying property valuations, the user cost model is limited in that it has no explicit role for financial intermediation or credit. Its implicit assumption is that there are no credit constraints or frictions, and consequently that households can move costlessly between the rental and owner-occupier markets. Needless to say, this is an unrealistic assumption.
An easy way to get intermediation into the user cost model is by way of the interest rate. The conventional way to think of intermediation is the process through which funds made available by savers are channelled to borrowers (in this case, prospective home buyers). As suggested by Woodford (2010), the supply of available funds is ‘produced’ by the financial sector, and this output is an increasing function of the spread between the rate paid by borrowers and that received by savers. In Woodford's framework, a positive ‘intermediation shock’ increases the amount of credit intermediaries are willing to supply for a given spread, which ceteris paribus decreases the interest rate paid by borrowers.[3] A plausible explanation of a housing boom is that it is the result of just such a favourable intermediation shock, transmitted through a reduction in interest rate spreads.[4] According to this view, it is the reduction in mortgage interest rates, via their effect on user cost, that accounts for the increase in housing prices.[5]
A natural way to model macroprudential and other policies in this framework is in terms of their effects on the supply of intermediated credit: presumably actions such as reductions in the maximum LTV or DSTI ratios would have a direct impact on the price and/or availability of credit. There are good reasons to believe that such measures may be preferable to the conventional interest rate instrument. First, changes in the short-term policy rate may have only small effects on the user cost, to the extent that the relevant interest rate is for a longer maturity. Second, unlike changes in the overall level of interest rates, macroprudential measures may be targeted more narrowly at the housing sector. The ability to intervene through these channels does not necessarily imply that it is optimal to do so, of course. That conclusion must rely on a more fully articulated macro model that links leverage with financial stability, such as that of Cúrdia and Woodford (2010).
4. Empirical Framework
This section describes the regression equations we will use to assess the effects of interest rates, institutional features of the housing finance system, and various policy actions on housing prices and credit. Our housing price specification is loosely based on the user cost model sketched above, extended informally to include variables capturing market structure and macroprudential policy changes. In the absence of a well-defined theoretical model, the housing credit regression is more of a reduced form. The regressions are intended to reveal answers to three questions: first, how sensitive housing prices are to the interest rate (and by extension, how much of the recent housing price boom is attributable to low interest rates); second, the importance of structural features in determining the effects of interest rates and demand; and third, the impact of macroprudential policies on housing prices and credit.
4.1 Modelling housing prices
The user cost model sketched in Section 3 is a sensible basis for any empirical assessment of the determinants of housing prices.[6] Specifically, our starting point is the basic static user cost relationship in Equation (2). Translating this equation into a regression model poses two challenges, however. The first is that a technically correct implementation requires tax rates, τy and τp, which may vary over time. The rate of depreciation, δ, could also be time-varying. Time series data for these variables are available for the United States, but obtaining the necessary information for our panel of 57 economies would be a herculean task. Furthermore, one would want to use expected inflation, πe, rather than the actual rate. Empirical work for the United States, such as that of Gallin (2008), has used survey data on long-run inflation expectations, but again those data are unavailable for most economies. Data limitations therefore require that we work with a simplified version of the user cost relationship:

which assumes constant depreciation and tax rates (subsumed into the intercept) and uses actual rather than expected inflation.
The second complication is that the risk premium, σt, and the expected rate of real appreciation, 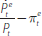 , are both unobserved. These terms are therefore
subsumed into the error term. Since these are unlikely to be white noise, the
model will have to incorporate some dynamics. If these terms and the interest
rate are stationary, then the rent-to-price ratio will also be stationary;
this in turn implies an error-correction model for Rt and
Pt. This is conventionally expressed in log-linear form:
, are both unobserved. These terms are therefore
subsumed into the error term. Since these are unlikely to be white noise, the
model will have to incorporate some dynamics. If these terms and the interest
rate are stationary, then the rent-to-price ratio will also be stationary;
this in turn implies an error-correction model for Rt and
Pt. This is conventionally expressed in log-linear form:
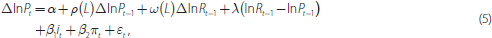
where Pt and Rt are real housing prices and rents, and ρ(L) and ω(L) are polynomials in the lag operator.
We will make five modifications to Equation (5) to capture the possibility of deviations from the simple user cost model and to incorporate the effects of regulation and financial structure.
First, in theory, shifts in the demand for housing services should be reflected in rent: a positive shift in demand, for example, would raise rents, and via the user cost relationship, housing prices should appreciate. This linkage is likely to be imperfect in practice, however. There may be frictions that lead to the sluggish adjustment of rents. In addition, the available rent data are imperfect, and probably do not accurately capture the rent that is relevant to households substituting between rental and owner-occupied housing. We therefore include lagged four-quarter-ended real personal income growth, lnyt−1 – lnyt−5, as an additional regressor to proxy for shifts in the demand for housing not captured in the rent data.
Second, according to the user cost model, the interest rate that determines housing prices is the (after-tax) mortgage rate. This is hard to measure, however, and obtaining the necessary data is difficult for many economies. Using a single interest rate is even problematic for the United States, given the expanding array of financing options (variable rates, ‘teaser’ rates, points-versus-interest rates, etc). Moreover, the option of refinancing affects the true cost of carrying a mortgage. As a crude way to take some of these factors into account, we include as regressors the mortgage rate im and a short-term interest rate, is.
Third, we allow for the possibility that certain structural factors may affect the demand for housing, and/or the responsiveness of housing prices to interest rates. As discussed below in Section 5, one of these variables is the economy's typical LTV ratio. However, to the extent that this is constant over time, this effect will be subsumed into the country-specific constant term. Another is the structure of mortgages, that is, whether they are typically fixed or variable rates. This suggests interacting the short-term and long-term interest rate variables with a variable capturing the prevalence of one type of mortgage or the other. The vector of structural features is denoted z.
Fourth, in order to gauge the effectiveness of the macroprudential policies that are the focus of this paper, we include a set of variables intended to capture the effects of maximum LTV and DSTI ratios, risk weights, provisioning, exposure limits, reserve and liquidity requirements, and taxes and subsidies related to housing. The vector of policy variables is denoted x. Section 5 describes these variables in greater detail. A discussion of exactly how these variables enter the regression will be deferred to Section 6.
Fifth, taking into account the likely lag in the effects of these variables on housing prices, the regressors are all lagged by one quarter.
With these five modifications, our regression specification for housing prices is:
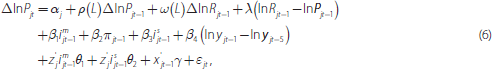
where the subscript j indexes the country. A country-specific intercept, αj, is included to capture time-invariant cross-country differences in housing price growth. To compensate for data imperfections, such as different rates of quality change for rental versus owner-occupied housing, the log of the rent-to-price ratio, lnRjt−1 – lnPjt−1, is detrended on a country-by-country basis.
4.2 Modeling housing credit
Our regression specification for housing credit growth is analogous to the housing price regression, but substitutes housing credit growth for housing price growth:
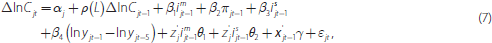
where ΔlnC represents the real growth rate of housing credit. Although not
derived from an explicit theoretical model, Equation (7) can be interpreted
as a reduced form of a model in which the volume of housing credit depends
on the price of owner-occupied housing. The same factors influencing housing
prices, such as interest rates and regulatory measures, should therefore also
affect housing credit. Macroprudential policies may affect prices and credit
differently, however, and so it will be interesting to compare the estimated
 with the results obtained
from the housing price regression.
with the results obtained
from the housing price regression.
Needless to say, Equations (6) and (7) are susceptible to the critique that the regressors
are likely to be endogenous. Specifically, policymakers may adjust interest
rates or implement macroprudential measures in response to conditions in the
housing market (or in response to omitted variables that are correlated with
housing price or credit fluctuations). This is especially true in those economies,
such as many in the Asia-Pacific region, where policymakers have actively changed
LTV ratios, provisioning and reserve requirements in their efforts to curb
housing market excesses. This endogeneity may bias the parameter estimates,
making it problematic to interpret the  coefficients as a reliable
gauge of the policies' effectiveness.
coefficients as a reliable
gauge of the policies' effectiveness.
Fortunately, there is reason to believe that the endogeneity problem will lead the estimates to understate these policies' effectiveness. Consider a tightening of the LTV requirement (a decrease in the maximum LTV ratio) for example. If the policy had the desired effect, it would reduce housing prices ceteris paribus. But if policymakers tended to tighten the LTV requirement when housing prices were already rising, this would give rise to a positive correlation between our LTV variable and housing prices, partially (or fully) offsetting the desired policy effect.[7] In the (implausible) limiting case in which policymakers managed to set the maximum LTV ratio in such a way as to completely stabilise housing prices, the estimated regression coefficient on the maximum LTV ratio variable would be zero. An accurate statistical assessment of the policies' effects would require some exogenous variation in the policy measures (regulatory ‘policy shocks’). Unfortunately, it is hard to think of any circumstances that would give rise to such exogenous policy shifts.
5. Data
Our econometric analysis spans the period from 1980:Q1 to 2011:Q1, and covers 57 advanced and emerging market economies. These include 13 economies from the Asia-Pacific region (Australia, China, Chinese Taipei , Hong Kong SAR, India, Indonesia, Japan, Malaysia, New Zealand, the Philippines, Singapore, South Korea and Thailand), 15 from central and eastern Europe (Bulgaria, Croatia, the Czech Republic, Estonia, Hungary, Latvia, Lithuania, Poland, Romania, Russia, Serbia, Slovakia, Slovenia, Turkey and Ukraine), 6 from Latin America (Argentina, Brazil, Chile, Colombia, Mexico and Peru), 2 from the Middle East and Africa (Israel and South Africa), 19 from Western Europe (Austria, Belgium, Denmark, Germany, Finland, France, Greece, Iceland, Ireland, Italy, Luxembourg, Malta, the Netherlands, Norway, Portugal, Spain, Sweden, Switzerland and the United Kingdom) and 2 from North America (Canada and the United States).[8] This section summarises the data sources and the criteria used for selecting the economies and sub-samples, and reports descriptive statistics for the key variables used in the analysis.
5.1 Data sources
One component of our dataset consists of time series data on housing and macroeconomic variables. In most cases, these data are available at a quarterly frequency. However, in some cases, annual or half-yearly data are interpolated to a quarterly frequency. A second component is a compilation of structural features of the housing market. The third is a compendium of all discrete macroprudential policy actions for each of the 57 economies.
Housing prices (P)
The primary source for housing price data is the BIS property price database. For economies not covered by BIS property price statistics, we also use housing price data from CEIC and national sources. For a few economies where official data on housing price indices are unavailable, we use housing price data from private sources. The definition of housing price indices varies across the economies. When multiple housing price indices are available for a given economy, for example nationwide versus major city indices, we use indices for major cities, as these are the areas that would be most susceptible to overvaluation and are often targeted by prudential and fiscal policy measures.
It goes without saying that these data are highly imperfect. Data construction methods (e.g. quality adjustment) vary greatly across the economies, as does the definition of the relevant housing market (e.g. apartments versus detached houses). Moreover, in some cases two or more series must be spliced together in order to yield an appropriate time series. In India, for example, we combined the Mumbai housing price series provided by the Reserve Bank of India, which ends in 2010:Q2, with a new price index from the National Housing Bank, which is available from 2010:Q3. Conclusions involving the level of property prices are therefore problematic, especially cross-country comparisons. Recognising these limitations, we will proceed on the assumption that these series can serve as informative indicators of cyclical swings in the residential property market, and that detrending the rent-to-price ratio compensates for data inadequacies, such as trend changes in housing quality.
Housing rent (R)
We use housing rental indices when available; otherwise, we use the housing rental component of the consumer price index (CPI) available from Datastream, Haver Analytics, Eurostat and other national sources. Needless to say, the construction of these indices varies across the economies. And, as is always the case in analyses involving user cost calculations, one worries about whether the housing rental component of the CPI is a good proxy for actual rent data.
Housing credit (C)
The primary sources of housing credit data are BIS Data Bank, Datastream, CEIC and central bank websites. Data are available for all 57 economies, although the time series dimension is often limited. Moreover, the sources and definitions are not always consistent, even within a economy.
Interest rates (im and is)
The user cost calculation described earlier requires a representative mortgage rate, denoted im, or some suitable gauge of the opportunity cost of home ownership. The availability of mortgage rate data is limited, however, both in terms of economy and time coverage. The results presented in this paper use the bank lending rate from the IMF's International Financial Statistics (IFS) database and national sources, which are available for all 57 economies in our sample, as a proxy for the mortgage rate. Most of the short-term interest rate series, is, are the money market interest rates from the IFS database. Where the IFS' coverage was incomplete, we used interest rates obtained from national sources and Haver Analytics. These short-term interest rates tend to move closely with the policy rate, while long-term lending rates may only indirectly reflect changes in the policy rate.
The price level and inflation (π)
The price level used for calculating the inflation rate is the CPI obtained from the IFS database. The CPI is also used to deflate the rent, property price and personal income series.
Personal income (y)
Ideally, we would use national household disposable income data to capture effective housing demand in each economy. Obtaining household disposable income data is difficult for a large number of economies, however. We therefore used instead annual real gross national income (GNI) per capita, obtained from the World Development Indicators database of the World Bank Group, as a proxy for personal income.[9] Quarterly series are obtained by interpolation, using compound growth rates.
Structural features of the housing finance system (z)
Because the level of development of national housing finance systems is likely to affect housing price cycles and housing credit availability, it is important to control for cross-country differences in these institutional features. Considering data coverage across the economies and the expected impact on housing price and credit cycles, we collected data on four variables: (i) the typical LTV ratio; (ii) whether loans are recourse or non-recourse; (iii) the typical maturity of mortgage contracts; and (iv) the prevalence of fixed- versus variable-rate mortgages.[10]
To the extent that they remain constant over time, these factors will be subsumed into the country-specific intercepts.[11] Consequently, we do not include the first three variables in the regression, on the assumption that they will get picked up in the country fixed effects.
Differentiating economies with fixed-rate mortgages from those with variable rates could be relevant, however, as housing prices and credit would be expected to respond differently to short- versus long-term interest rates. In particular, one would expect the short-term policy rate to have a larger effect on the housing market in economies with predominantly variable-rate mortgages. To capture this possibility, we will interact the interest rate variables im and is with a (time-invariant) variable reflecting the typical mortgage structure. The variable is assigned the value 1 for economies with predominantly variable-rate mortgages, 0 for those with fixed-rate mortgages, and 0.5 for those with a mix of the two types.
Policy measures (x)
One of the major contributions of the paper is the compilation of a monthly database on policy measures introduced to affect housing credit and housing price cycles. We consider both tightening and loosening policy actions. In particular, we collected the following three broad types of measures:
- non-interest rate monetary policy measures: average or marginal reserve requirements on domestic and foreign currency liabilities plus liquidity requirements,[12] and limits on credit growth;
- prudential policy measures: maximum LTV ratios, maximum DSTI ratios, risk weights on housing loans, provisioning requirements (general loan-loss provisioning ratios and specific provisioning ratios applied to housing loans), exposure limits on banks to the housing/property sector; and
- fiscal policy measures: capital gains taxes at the time of the property sale, wealth taxes, other taxes related to housing purchase or sale, such as stamp duties, and other legal fees and government subsidies related to housing purchases.
It should be noted that monetary and prudential policy measures mentioned in (i) and (ii) directly affect credit supply to the housing sector and thus housing demand by households. By contrast, fiscal measures in (iii) affect housing transactions through more or less cash payments.
Our database of policy actions draws on a variety of sources. The primary source is official documents from central banks and regulatory authorities, including annual reports, financial stability reports, monetary policy bulletins, supervisory authorities' circulars, ministry of finance announcements on tax changes and press releases from these institutions. We also consulted Borio and Shim (2007), a survey by the Committee on the Global Financial System (CGFS) on macroprudential policy conducted in December 2009, and IMF research papers. Where these secondary sources were used, we cross-checked the information against the information obtained from official documents.[13] We then used our database of policy actions to generate variables capturing the tightening and loosening of the policy instruments.
Heterogeneity is an inherent feature of this database. Even applying consistent selection criteria across economies, the specifics of policy actions differ across economies and over time. Naturally, including these data in a regression model requires some degree of standardisation and aggregation. Our solution is to create a monthly binary variable that takes on the value of 1 for tightening actions, and −1 for loosening actions.[14] A measure of the stance of policy can be calculated as the accumulation of past changes. This is analogous to looking at the level of the policy interest rate, which is the accumulation of past changes in the policy rate.
5.2 Sample selection criteria
The main limiting factor in the creation of our combined dataset is data availability. This is particularly relevant for housing price, rent and housing credit data, which have only recently begun to be collected in many economies. In a few cases, the binding constraint is the lack of interest rate data. Because personal income data are only available until 2010:Q4, our analysis ends in 2011:Q1.
Even where data are available, there are often good reasons to discard a portion of the sample. One is in cases of extreme macroeconomic instability, such as periods of very high inflation rates. This is a concern in seven countries: Argentina (in both 1990 and 2002), Brazil, Bulgaria, Croatia, Indonesia, Mexico and the Philippines, all of which experienced annualised inflation rates of 50 per cent or more (much more in the case of Argentina).
Data quality is another issue. While there is no good way to independently verify the reliability of the data, many of the series exhibit discontinuities or extremely high volatility (annualised changes sometimes in excess of 100 per cent). Some of the observed spikes may be the result of very rapid growth from a small base, a characteristic of several CEE countries. High property price volatility may be due to small samples and/or thin markets, which is surely an issue in the early part of the sample for many transition economies. Not all large changes in housing prices or credit are due to data anomalies, however. In Estonia, for example, housing prices fell by 22 per cent in a single quarter in 2009, reflecting the collapse of the real estate market. Similarly, the 45 per cent decline in Iceland's housing credit in one quarter of 2008 is consistent with that country's property market implosion. It would therefore be inappropriate to tag all large changes in housing prices or housing credit as outliers. Instead, we exercise our judgment in distinguishing between spurious and bona fide jumps in the series. Where anomalies occur only in the early part of the sample, the start date is moved up; otherwise, either a break adjustment is added, or the observation is replaced with a missing value.
For some economies, data are available, but the time series are too short to be of any use. Brazil, for example, has only 4 quarterly observations of housing price data. And dropping the first few highly volatile housing credit observations leaves only 11 data points for Ukraine and Serbia. Economies with fewer than 18 usable observations are excluded from the regression analysis.
5.3 Data description
Table 2 shows a tally of the different types of policy actions, aggregated by region.[15] The key features of the dataset are the following:
- The dataset contains a total of 662 policy actions in all, of which roughly two-thirds are tightening and one-third loosening.
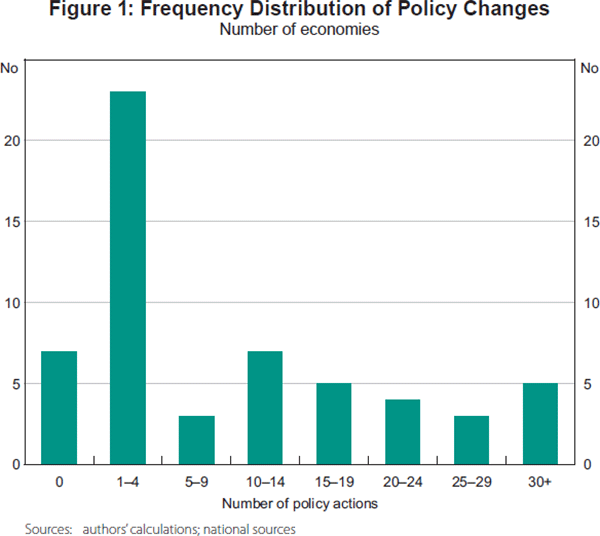
- As shown in Figure 1, a large share of the economies in the sample used macroprudential policies only occasionally, if at all. A handful of economies were very active users of these policies, with 30 or more documented policy actions.
- Most of the policy changes in the dataset were taken by these very active users. Nearly one-third of all the actions are attributable to the top 5 users. The top 18 economies (each with 15 or more actions) account for three-quarters of the sample.
- The most active users of these policies are the Asian and CEE economies. Among Latin American countries, Chile and Peru are the most frequent users; in Western Europe, Finland and Norway account for the majority of the actions.
- Reserve requirements are by far the most frequently used of the nine categories of policies, accounting for more than half of all the policy actions. Liquidity requirements and credit growth restrictions are seldom used. Among the prudential policies, LTV and DSTI restrictions are most popular, followed by risk weights, provisioning and exposure limits.
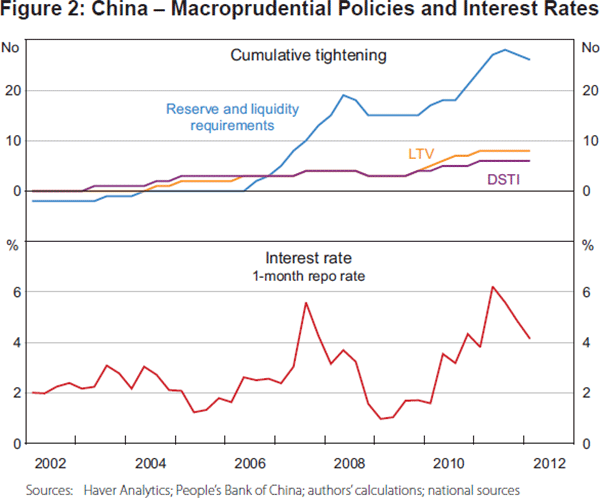
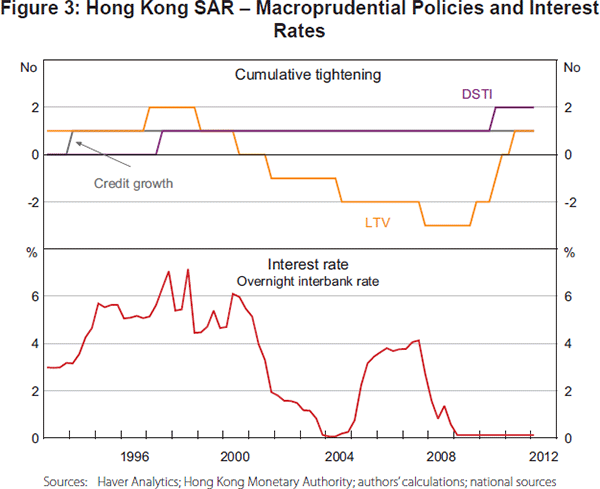
To give a sense of how these policies have been implemented in practice, Figures 2 to 4 display the relevant cumulative policy actions along with the short-term nominal interest rate for a few Asian economies. The figures convey the diversity of economies' deployment of these policies. They have been used to complement conventional interest rate policy during some episodes, while during others they have functioned as substitutes. Similarly, the various macroprudential tools have sometimes been used in concert, and independently at other times.
| Prudential | ||||||
|---|---|---|---|---|---|---|
| LTV ratio |
DSTI ratio |
Risk weights |
Provision | Exposure | Total | |
| Asia-Pacific (13) | 46 | 19 | 13 | 10 | 8 | 96 |
| CEE (15) | 11 | 15 | 16 | 7 | 5 | 54 |
| Latin America (6) | 1 | 0 | 3 | 3 | 1 | 8 |
| Middle East/Africa (2) | 0 | 0 | 3 | 1 | 0 | 4 |
| Western Europe (19) | 5 | 2 | 5 | 3 | 0 | 15 |
| North America (2) | 4 | 2 | 0 | 0 | 0 | 6 |
| Total (57) | 67 | 38 | 40 | 24 | 14 | 183 |
| Monetary | Fiscal | Total | ||||
|---|---|---|---|---|---|---|
| RR | Liquidity | Credit | Total | |||
| Asia-Pacific (13) | 129 | 3 | 3 | 135 | 41 | 272 |
| CEE (15) | 150 | 1 | 7 | 158 | 12 | 224 |
| Latin America (6) | 48 | 0 | 0 | 48 | 0 | 56 |
| Middle East/Africa (2) | 0 | 0 | 0 | 0 | 0 | 4 |
| Western Europe (19) | 70 | 5 | 0 | 75 | 4 | 94 |
| North America (2) | 5 | 0 | 0 | 5 | 1 | 12 |
| Total (57) | 402 | 9 | 10 | 421 | 58 | 662 |
| Notes: Covers 57 economies; figures represent the number of discrete policy changes falling into each category, with a maximum of one count per month per measure; based on preliminary and incomplete data as of 11 August 2012; RR refers to reserve requirements | ||||||
In China (Figure 2), for example, the short-term interest rate, reserve requirements, the maximum LTV ratio and DSTI requirements have all tended to move in the same direction: tightening in 2006–2008, loosening in 2008–2009, and tightening from 2010. The relationship between the LTV and DSTI measures is particularly close. Since 2002, there has been a steady trend towards more restrictive policy on all three non-interest rate dimensions.
In Hong Kong SAR (Figure 3), the tightening of the credit growth limits was the only monetary tool used in 1993. Prudential measures (mostly changes in the maximum LTV ratio) were used actively from the mid 1990s, usually in parallel with the general direction of interest rates in Hong Kong (as well as those in the United States). The opposite has been true since 2009: the LTV requirements have been progressively tightened even as the short-term interest rate has remained around zero (tracking the US rate). Hong Kong authorities have also made more active use of tax measures since 2009.
In Korea (Figure 4), reserve requirements were the primary macroprudential tool used throughout the late 1980s and 1990s, rising along with the short-term interest rate (except during the Asian financial crisis). Since 2002, the short-term interest rate has remained stable, but the DSTI and LTV ratios have been tightened considerably. Both ratios followed a similar upward trajectory, although the tightening in the LTV requirements started roughly three years prior to the tightening of the DSTI requirements. As in China, the LTV and DSTI requirements are both significantly more restrictive now than they were 10 years ago.
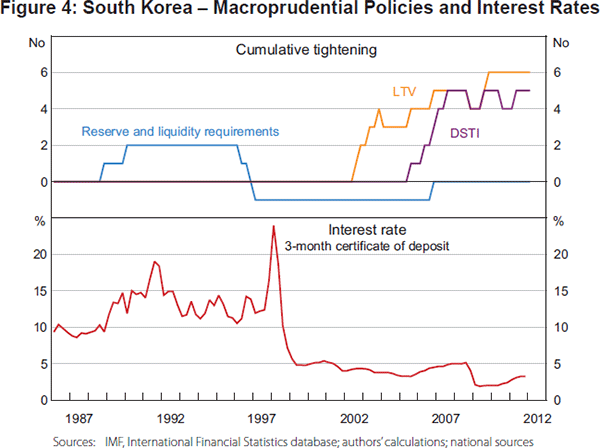
Table 3 displays descriptive statistics for the seven housing and macroeconomic variables, calculated for the economies included in the subsequent regression analysis.[16] Clearly, there is a great deal of volatility in the housing price and credit growth data, even after deleting the obvious anomalies. (It may come as no surprise that Iceland is responsible for the minimum and maximum values of real housing credit growth.) Even rent growth has exhibited some very large swings in our sample.
| Mean | Std dev |
Fractiles | Obs | |||||
|---|---|---|---|---|---|---|---|---|
| Median | 5% | 95% | Min | Max | ||||
| Real housing price growth |
1.6 | 12.8 | 1.4 | −17.4 | 20.4 | −100.8 | 82.3 | 3,650 |
| Real rent growth | 0.6 | 7.3 | 0.2 | −7.3 | 11.1 | −70.8 | 66.4 | 3,373 |
| Short-term interest rate |
5.9 | 4.8 | 4.7 | 0.5 | 15.2 | 0.0 | 39.5 | 3,956 |
| Lending rate | 9.1 | 5.5 | 7.6 | 3.2 | 19.5 | 0.5 | 45.9 | 3,956 |
| Inflation | 3.9 | 3.6 | 2.9 | 0.0 | 10.9 | −6.3 | 27.8 | 3,932 |
| Real personal income growth |
2.3 | 3.3 | 2.4 | −3.3 | 7.6 | −19.3 | 14.8 | 3,703 |
| Real housing credit growth |
9.5 | 16.2 | 7.3 | −7.9 | 37.1 | −260.2 | 141.4 | 3,595 |
| Note: Real housing price growth, real rent growth, real personal income growth, real housing credit growth and inflation are annualised quarterly growth rates | ||||||||
6. Results
Section 4 left unresolved the question of exactly how the macroprudential policy variables (x) would enter the model. Having provided details on the construction of those variables, we are now in a position to revisit that question.
One issue concerns the level of aggregation across types of policies discussed in Section 5. While we have collected data on nine distinct types of macroprudential policy actions, some of those policies have been used very infrequently. We observed only nine changes in liquidity requirements, for example, and eight changes in credit growth limits. Rather than try to estimate the effects of these rarely used policies, we combine them with the reserve requirement variable to create a composite measure of non-interest rate monetary policies. Each of the five prudential variables is included separately in the regression. These five prudential variables plus the fiscal and non-interest rate monetary variables make a total of seven variables comprehensively capturing important policy measures affecting housing markets.
Table 4 shows the pairwise correlations between the seven policy variables. Most are relatively low, indicating either that they have been used independently of one another, or that different economies tend to use different policy tools. A notable exception to this pattern is the correlation between the maximum DSTI and LTV ratios, which is 0.63. This suggests that these two tools in particular have often been used in tandem, as seen in the cases of China and Korea.
| Monetary | Fiscal | LTV ratio |
DSTI ratio |
Risk weights |
Provision | Exposure | |
|---|---|---|---|---|---|---|---|
| Monetary | 1 | 0.04 | 0.23 | 0.22 | 0.03 | 0.16 | −0.13 |
| Fiscal | 1 | −0.05 | 0.09 | −0.04 | 0.03 | −0.07 | |
| LTV ratio | 1 | 0.63 | 0.03 | 0.19 | 0.09 | ||
| DSTI ratio | 1 | 0.07 | 0.26 | 0.11 | |||
| Risk weighting | 1 | 0.19 | −0.10 | ||||
| Provisioning | 1 | 0.15 | |||||
| Exposure limits | 1 | ||||||
| Note: See notes to Table 2 | |||||||
Another issue is how to count multiple policy changes occurring within a quarter. There are two ways to aggregate the monthly data into quarterly time series. The first is to accumulate every policy action, even when there are multiple actions within a quarter; three consecutive policy tightening actions would make the quarterly series jump by 3. Economies that took a large number of incremental actions, such as China, will therefore exhibit large changes in the index constructed in this fashion. An alternative is to assign the value 1 to any quarter in which a tightening action takes place, even when there are multiple changes within the quarter. The results presented below use the latter method, on the grounds that counting every policy action would give undue weight to economies, such as China, that made a large number of incremental changes.[17]
A more subtle issue concerns the way in which the macroprudential variables are included in the regression, that is, as dummies for each individual policy action, or as the accumulation of past changes (as shown in Figures 2 to 4). The choice will affect the estimated persistence of the policies' impact on the dependent variables, which are both expressed as growth rates. To see why, suppose the LTV requirement is tightened (i.e. the maximum LTV ratio is reduced) in a particular quarter, so that the LTV dummy takes on a value of 1 in that quarter, and zero afterwards. Using this dummy variable ‘as is’ in the regression implies that the policy action will have only a transitory effect on the dependent variable (real housing price growth or real housing credit growth); over time, the rent-to-price ratio will return to its previous level, ceteris paribus. If the regression includes a variable defined as the accumulation of past policy changes, on the other hand, then the rent-to-price ratio will be permanently affected by the tightening of the LTV requirements (in the absence of a subsequent reversal). Rather than choose between the two approaches, we remain agnostic about the persistence of the policies' effects by including the variable representing the change in the policy and the variable constructed by the accumulation of past changes.
All of the specifications allow for country-specific intercepts (country fixed effects).[18] In principle, the presence of the lagged dependent variable creates the possibility of bias. But given that the time series dimension of the data is relatively large, in practice this should not be a major problem. We therefore follow Goodhart and Hofmann (2008) in estimating the model via ordinary least squares (OLS).
As noted earlier, the samples over which the regressions are estimated are determined primarily by data availability, and some of the observations that appear to be unreliable are deleted. The full sample uses data going back as far as 1980 for Australia, Canada and the United States. Other economies' data start as late as 2007. Only those economies for which at least 18 time series observations are available are included. We also estimated the models on a sub-sample ending in 2007:Q2. The rationale for analysing the truncated sample is to ensure that the results are robust to the exclusion of the recent financial crisis, which of course was accompanied by a collapse of the housing market in many of the economies we analysed. The sample split could potentially shed some light on the possibility of asymmetries in the effects of policies during booms versus busts.
6.1 Housing prices
Table 5 displays the results for the housing price model (Equation (6)). The first column reports the estimates for the full sample, which includes 399 observations with non-zero values of the macroprudential policy variables.[19]
The results show that interest rates have statistically significant effects on housing prices. A 1 percentage point increase in the short-term interest rate is associated with a 0.7 percentage point reduction in housing price growth in economies with predominantly variable-rate mortgages, and a 0.9 percentage point reduction for those with predominantly fixed-rate mortgages. The coefficients on the lending rate variables are positive but comparable in magnitude to those on the short-term rate, suggesting that it is the spread between short-term and lending rates that is most closely associated with housing price fluctuations.[20] The magnitude of these effects is modest, however. Consistent with the research summarised in Section 2, the estimates are smaller than those implied by the user cost model, and suggest that interest rates cannot fully explain the observed booms and busts in housing prices.
Among the macroprudential policy measures, the LTV and exposure limit variables are the only ones with statistically significant effects. The coefficient on the cumulative LTV measure suggests that a permanent reduction in the allowable LTV ratio would slow housing price appreciation by roughly 1.5 percentage points. The coefficient of 0.6 on the lagged four-quarter-ended growth rate of housing prices suggests that the long-run impact of a permanent tightening could be in the order of −4 percentage points, assuming that none of the other right-hand side variables respond. This is a substantial reduction, and roughly twice the impact of a 1 percentage point rate hike. It should be noted that in our database on policy measures, a typical tightening or loosening of the LTV requirements corresponds to approximately a 10 percentage point change in the maximum LTV ratio. The estimated impact of a tightening is nonetheless quite modest relative to the double-digit growth rates in housing prices experienced in many economies during the height of the boom. The coefficient of −9.8 on the change in the exposure limit variable suggests a large but transitory effect on housing price growth. But with a relatively small number of non-zero observations on this variable, one should not attach too much weight to this result.
The general lack of statistical significance among the other policy variables would seem to indicate that they have no effect on housing price growth. The statistical significance of individual parameter estimates does not give the complete picture, however; in fact, the five variables in the prudential category (maximum LTV ratio, maximum DSTI ratio, risk weights, provisioning, and exposure limits) are jointly significant (with a p-value of less than 0.01 per cent). One can therefore conclude that, taken together, changes in the prudential policies do have a discernible effect on housing price growth. However, because these policies are often deployed concurrently, as illustrated in Figures 2 and 3, it is hard to distinguish econometrically the effects of each one individually.
As noted above, economies differ greatly in their tendency to utilise macroprudential policy tools, and a relatively small number of economies account for the lion's share of policy actions in our database. To see whether the measured effectiveness of these policies varies on this dimension, we re-ran the regressions on data from a group of 18 active users, defined as those with 15 or more policy actions. Although the number of observations is only one-quarter of the full sample, this sub-sample includes over 70 per cent of all the macroprudential policy changes.
The second column of Table 5 reports the results from the regression on the sub-sample of active users. Reassuringly, the results are quite similar to those based on the entire sample, but there is stronger evidence of macroprudential policies' effectiveness: the coefficient on the cumulative LTV variable is now significant at the 1 per cent level. Fiscal measures and exposure limits also have more pronounced effects. One anomaly is the positive (but only marginally statistically significant) effect of tightening provisioning requirements.
Another interesting question is whether the effects of macroprudential policies have changed since the recent financial crisis of 2007–2009. We investigate this possibility by re-running the regression on a sub-sample ending in 2007:Q2. Because of the more frequent use of macroprudential policies in recent years, truncating the sample in this way reduces the total number of observations by 27 per cent, but cuts the number of policy actions used in the regression by 55 per cent (from 399 to 178).[21]
The third column of Table 5 displays the results from the pre-crisis regression. The results are generally similar to those from the full-sample regression. In spite of the smaller number of observations, the cumulative LTV variable remains significant at the 5 per cent level, and is somewhat larger in magnitude (−2.6 compared with −1.5). The exposure limit variable remains highly significant. Puzzlingly, tightening provisioning requirements again appears to be associated with more rapid housing price growth.
| Regressor | Full sample |
Active users |
Through to 2007:Q2 |
|
|---|---|---|---|---|
| Real housing price growth | 0.59*** | 0.53*** | 0.56*** | |
| Real rent growth | −0.35*** | −0.43*** | −0.40*** | |
| VR x (Short rate) | −0.72*** | −0.93*** | −0.95*** | |
| VR x (Lending rate) | 0.35* | −0.58 | 0.36** | |
| (1 – VR) x (Short rate) | −0.91*** | −2.05*** | −0.19*** | |
| (1 – VR) x (Lending rate) | 0.71* | 3.78* | −0.34* | |
| Inflation | −0.06 | −0.28 | 0.54*** | |
| Real income growth | 0.16 | 0.51 | −0.07 | |
| Rent/price ratio | 0.19*** | 0.33*** | 0.17*** | |
| Monetary: | Change | −0.03 | 0.40 | 2.75** |
| Cumulative | 0.08 | 0.21 | 0.39 | |
| Fiscal: | Change | 3.43 | 4.05 | 2.96 |
| Cumulative | −1.41 | −4.09*** | −0.60 | |
| LTV ratio: | Change | −0.82 | −0.37 | −6.48 |
| Cumulative | −1.48** | −1.70*** | −2.56** | |
| DSTI ratio: | Change | 2.88 | 1.80 | 4.59 |
| Cumulative | 0.43 | 0.74 | 0.50 | |
| Risk weights: | Change | −6.29 | −9.88 | −3.72** |
| Cumulative | −0.44 | 1.22 | 1.19 | |
| Provisioning: | Change | 1.37 | 1.74 | 4.00 |
| Cumulative | 2.26 | 6.32* | 3.93** | |
| Exposure limits: | Change | −9.84** | −7.73 | −13.45*** |
| Cumulative | −3.45 | −4.06*** | −2.28 | |
| Prudential variables' joint significance | 0.000 | 0.000 | 0.000 | |
| Number of policy actions | 399 | 284 | 178 | |
| Observations | 2,814 | 664 | 2,040 | |
| Standard error of housing price growth | 13.3 | 19.3 | 10.4 | |
| Adjusted R-squared | 0.241 | 0.268 | 0.276 | |
| Notes: ***, ** and * indicate statistical significance at the 1, 5 and 10 per cent level, respectively, based on robust standard errors. The regression also includes country fixed effects. The VR variable is set equal to 1 for economies with predominantly variable-rate mortgages, 0 for economies with predominantly fixed-rate mortgages, and 0.5 for economies with a mix of both types. The results are based on data from 55 economies for the period 1980:Q1–2011:Q1 (the time dimension varies by economy). The set of active macroprudential policy users includes the 18 economies with 15 or more documented macroprudential policy actions. | ||||
6.2 Housing credit
Table 6 displays the results from estimating the housing credit model (Equation (7)). The first column reports the results for the full sample of 55 economies through to 2011:Q1.[22]
| Regressor | Full sample |
Active users |
Through to 2007:Q2 |
|
|---|---|---|---|---|
| Real housing credit growth | 0.65*** | 0.82*** | 0.67*** | |
| VR x (Short rate) | −0.38** | −0.57 | −0.48** | |
| VR x (Lending rate) | 0.08 | −0.01 | 0.20 | |
| (1 – VR) x (Short rate) | −1.56** | −5.25* | −0.55** | |
| (1 – VR) x (Lending rate) | 1.43** | −1.51 | 0.50* | |
| Inflation | 0.07 | 0.15 | 0.04 | |
| Real income growth | 0.40** | 0.12 | 0.11 | |
| Monetary: | Change | −0.43 | −0.99 | −0.47 |
| Cumulative | 0.24 | 0.04 | 0.08 | |
| Fiscal: | Change | −3.14 | −0.53 | −3.48 |
| Cumulative | −0.26 | −0.26 | 0.14 | |
| LTV ratio: | Change | 0.44 | −3.10 | −2.34 |
| Cumulative | 0.51 | −0.20 | −0.04 | |
| DSTI ratio: | Change | −7.85*** | −5.11* | −4.38 |
| Cumulative | −3.36** | −0.92 | −5.24*** | |
| Risk weights: | Change | 1.02 | −1.63* | −1.85 |
| Cumulative | −1.94* | −2.54 | −0.18 | |
| Provisioning: | Change | −2.28 | −5.58** | −3.42 |
| Cumulative | −3.14*** | −1.86*** | −1.17 | |
| Exposure limits: | Change | 0.68 | 3.33 | −0.35 |
| Cumulative | −1.73 | −0.87 | −2.11 | |
| Prudential variables' joint significance |
0.000 | 0.000 | 0.000 | |
| Number of policy actions | 439 | 318 | 218 | |
| Observations | 3,223 | 707 | 2,454 | |
| Standard error of housing price growth | 15.6 | 18.7 | 9.0 | |
| Adjusted R-squared | 0.502 | 0.654 | 0.635 | |
| Notes: ***, ** and * indicate statistical significance at the 1, 5 and 10 per cent level, respectively, based on robust standard errors. The regression also includes country fixed effects. The results are based on data from 55 economies for the period 1980:Q1–2011:Q1 (the time dimension varies by economy). The set of active macroprudential policy users includes the 18 economies with 15 or more documented macroprudential policy actions. | ||||
Income growth and interest rates have significant effects on credit growth in the full-sample regression. Increases in the short-term interest rate have a larger dampening effect than the lending rate in economies with variable-rate mortgages, while the spread between the short-term and lending rates appears to be most relevant for economies with predominantly fixed-rate mortgages. And as in the housing price regressions, the magnitude of the effect is small: in the order of a 1 percentage point reduction in annualised real credit growth for a 1 percentage point increase in the short-term interest rate.
With regard to the macroprudential variables, the most pronounced effects on credit growth are associated with changes in the DSTI requirements. The coefficient on the variable reflecting the policy change indicates that tightening the DSTI requirements reduces annualised credit growth by roughly 8 per cent in the following quarter, and the coefficient on the cumulative variable is consistent with a −3 per cent long-run response to a permanent tightening. Increasing provisioning requirements also seems to slow credit growth by roughly the same amount. These findings contrast with those from the housing price regressions, in which the DSTI and provisioning variables had little discernible impact in the expected direction. The coefficients on the fiscal variable have the correct sign, suggesting that property-related tax increases temporarily slow credit growth. The estimates are not statistically significant, however. The five variables in the prudential category are jointly highly significant, but this is entirely due to the inclusion of the DSTI and provisioning variables; the remaining three are not collectively significant.
Results from a regression limited to active users of macroprudential policies, those with 15 or more such actions, are shown in the second column of Table 6. The results are similar to those from the full sample, which is not surprising given that this set of 18 economies accounts for roughly three-quarters of all the policy actions. The coefficients on the provisioning variables are statistically significant at the 5 per cent level or better, but that on the DSTI variable is only significant at the 10 per cent level. This is again somewhat misleading, however, as the five prudential variables are again jointly significant at a very low level (a p-value of less than 0.001). In fact, the exclusion restriction on just the LTV and DSTI variables can be rejected at less than the 0.1 per cent level.
The third column of Table 6 reports the results from a regression with the pre-crisis sample ending in 2007:Q2. Reassuringly, the results are very similar to those from the full sample, despite the 50 per cent reduction in the number of observations with non-zero policy actions. The coefficient on the cumulative DSTI variable is again large and highly significant. Neither of the provisioning variables is individually statistically significant, but it turns out that they are jointly significant at the 1 per cent level. Finally, neither of the exposure limit variables is individually statistically significant, but they are jointly significant at the 5 per cent level, suggesting that exposure limits were associated with slower credit growth before the recent financial crisis. This finding is in line with the results from the housing price regression over the same period.
6.3 Discussion
Taken together, two general conclusions emerge from the housing price and housing credit regressions reported above. The first is that the policies categorised as prudential measures (maximum LTV and DSTI ratios, provisioning requirements, real estate exposure limits and risk weights) collectively exhibit a strong link to housing price and credit fluctuations. This is evident from the fact that they are jointly highly statistically significant in every regression.
The exact form of that relationship is a little less clear, however. In some cases, it is because the level of the policy variables seems to matter, whereas in other cases the change appears to be more relevant. In addition, the tendency for some of the policies to be used in conjunction with one another – particularly the maximum DSTI and LTV ratios – makes it hard to disentangle the individual effects. The likely endogeneity of the policy changes further complicates the estimates' interpretation. It is therefore hazardous to read too much into individual parameter estimates.
Having said that, one interesting finding is that policy actions involving the LTV ratio appear to have had a more direct effect on housing prices than those involving the DSTI ratio, which have had a more readily discernible impact on the volume of credit. One explanation may simply be that the LTV requirements become more binding when housing prices outstrip appraised values, thus limiting the ability to finance purchases in an environment of rapidly rising prices. Measures limiting credit growth on the basis of other criteria would presumably have a less direct effect on prices.
The second general conclusion is that these prudential measures affect housing prices and housing credit, whereas non-interest rate monetary policy measures, including reserve requirements, do not – or at least not independently of interest rate policy. Given that the prudential policies are all aimed squarely at the housing market, this result should not be too surprising: all either affect borrowers' ability to obtain credit to finance housing purchases (DSTI and LTV requirements) or influence banks' cost of providing that credit (risk weights, exposure limits and provisioning requirements).
The same observation applies to fiscal tools, such as transaction taxes, which are also targeted specifically at the housing market. In principle, tightening these policies should make speculative activity more costly, and thus limit housing booms. Their efficacy should also be enhanced by the fact that they require relevant parties to pay tax in cash, affecting their cash flows directly.[23] The parameter estimates are consistent with this channel, although the regressions were unable to consistently establish a statistically significant impact.
7. Conclusion
The past decade's housing boom and bust has left central banks and regulators searching for non-interest rate policy tools capable of taming housing market excesses. Naturally, the focus has been on a variety of macroprudential measures, such as maximum LTV and DSTI ratios, that are targeted specifically at housing finance. Although some of these tools have been found to have had an impact in specific markets, until now there has been no global assessment of these policies' effectiveness. The goal of this paper has been to provide such an appraisal. The experiences of the Asia-Pacific economies are particularly salient in our analysis, as they have been in the forefront of the implementation of macroprudential policies.
In order to undertake our analysis, we constructed a comprehensive longitudinal database of the macroprudential policy actions by 57 economies taken over the past 30 years, and a complementary database of structural features of the housing finance system. Combining these data with time series on housing prices, rent, housing credit and interest rates gives us a detailed picture of the key macroeconomic, institutional, monetary, and regulatory factors affecting housing markets globally.
The results establish a link between interest rates and macroprudential policy actions and subsequent fluctuations in real housing prices and real housing credit. Higher short-term interest rates tend to slow housing price appreciation and housing credit growth, although the magnitude of the effect is modest. Actions categorised as prudential measures (maximum LTV and DSTI ratios, provisioning requirements, real estate exposure limits and risk weights) are consistently jointly significant in our regressions. Decreases in the maximum LTV ratio are associated with reductions in the growth rate of housing prices. Similarly, reductions in the maximum DSTI ratio and increases in provisioning requirements are associated with reductions in the growth rate of real housing credit. We were unable to find any consistent relationship between changes in non-interest rate monetary policy measures and either housing price or credit growth, however. Taken together, our results suggest that certain types of macroprudential policies can be effective tools for stabilising housing price and credit cycles. This is good news for central banks seeking additional flexibility in their pursuit of macroeconomic and financial stability objectives.
The results reported in this paper are only a first step to understanding the effects of macroprudential policies on the housing market. One possible refinement will be to replace the tightening/loosening dummy variables used in the analysis with numerical variables. In particular, the policy measure database allows us to construct numerical variables of LTV ratios, DSTI ratios, risk weights, loan-loss provisions, reserve requirements, and tax code changes. We also intend to explore the possible effects of the central bank's balance sheet on the supply of credit by including the monetary base in the analysis. Investigating possible asymmetries in the responses of housing prices and housing credit to policy actions during booms versus busts is another promising direction.
A country-level event-study analysis could also be an informative complement to our panel regression approach. Such an approach would resemble the perspective of policymakers, who tend to focus on the current housing market cycle in their own jurisdiction, and closely track the policy's effects for a period of one to two years after its implementation. One advantage of this approach is that it would allow us to look into whether the same measures were effective in each economy. Another is that it could shed light on the circumstances that led the authorities to take particular actions.
Footnotes
We are grateful for comments by seminar participants at the Bank for International Settlements. We thank Bilyana Bogdanova, Marjorie Santos, Jimmy Shek and Agne Subelyte for their excellent research assistance. The views presented here are solely those of the authors and do not necessarily represent those of the Bank for International Settlements. [*]
Following FSB-IMF-BIS (2011), macroprudential policy is characterised by reference to the following three defining elements: (i) objective – to limit systemic risk; (ii) scope – the focus is on the financial system as a whole; and (iii) instruments and associated governance – it uses primarily prudential tools calibrated to target the sources of systemic risk. In this paper, we use the term ‘macroprudential policy’ to refer to non-interest rate monetary policy, prudential policy and fiscal policy designed to influence housing prices and housing credit. [1]
These VAR-based estimates are comparable to those obtained by Glaeser, Gottlieb and Gyourko (2010) using a simple regression of the log housing price on the real 10-year interest rate. The estimates of Glaeser et al indicate that a 10 basis point reduction in the mortgage interest rate (roughly the rate reduction associated with a 25 basis point expansionary monetary policy shock) would result in a 0.7 per cent rise in housing prices. [2]
In this framework, the ‘risk-taking’ channel described by Borio and Zhu (2008) and others could be interpreted as a mechanism through which the reduction in the risk-free rate also causes an outward shift in the supply of intermediated credit. [3]
An increase in credit supply would not be fully manifested in spreads to the extent that credit became available to previously credit-constrained households. [4]
It is worth mentioning that an increase in the supply of credit, if it increased the flow supply of new housing, could lead the housing market to adjust more quickly to changes in the demand for housing. [5]
This is also the approach taken in Girouard et al (2006) and Sveriges Riksbank (2011). [6]
Indeed, an interesting direction for future research would be to estimate a regulatory ‘reaction function’ for those countries that make active use of such measures. [7]
We also have information on macroprudential policy measures taken in Uruguay, Saudi Arabia and the United Arab Emirates, but we currently lack other data, such as housing prices and interest rates, that would allow us to include these countries in the regression analysis. [8]
A further refinement, not made in this analysis, would be to subtract debt service flows from household income, if necessary, by approximating debt service as the product of outstanding household debt and a relevant loan rate. [9]
This is a subset of the range of variables considered in other studies such as Crowe et al (2011) and IMF (2011). [10]
Of course, these features may have changed over time, especially in emerging market economies with rapidly evolving financial systems. Incorporating time-varying structural features in the regression is straightforward, but documenting the changes over time is difficult. [11]
Liquidity requirements (typically, the minimum ratio of ‘highly liquid assets on a bank's balance sheet’ to ‘certain types of liabilities’) are a form of prudential regulation dealing with cash outflow shocks. Under minimum reserve requirements, banks are required to hold a fraction of their deposits/liabilities as liquid reserves. These are normally held at the central bank in the form of cash or highly liquid sovereign paper. When applied to deposits, the regulation usually specifies the size of the requirement according to deposit type (e.g. demand or time deposit) and its currency denomination (domestic or foreign currency). Reserve requirement rules also set the reserve maintenance period relative to the reserve calculation period against which reserve holdings are averaged for the purpose of satisfying reserve requirements, and specify whether they are remunerated or not. Reserve requirements are typically classified as monetary policy tools controlling the supply of credit by banks, not necessarily related to liquidity shocks. However, reserve requirements are very similar to liquidity requirements in terms of economic effects. Moreover, the number of observations related to liquidity requirements in our policy database is very small. Therefore, we merged the liquidity requirement observations into the reserve requirement variable. [12]
The dataset is still preliminary and incomplete at this point. We have so far compiled potentially relevant policy actions from the national sources for 52 economies. The results in this paper are based on relevant data for 42 economies, which were verified and selected under consistent criteria across economies, and provisional and/or incomplete data for the remainder. [13]
Some of the policy measures that are more standard across economies, such as reserve requirements, would be more amenable to a numerical representation. [14]
These figures are based on incomplete or unverified information, and are likely to change as new data are incorporated. See footnote 12. [15]
Gaps in the availability of some of the data further reduce the number of economies used in specific regressions. [16]
We obtain similar results with both methods. [17]
Results including time fixed effects are similar. [18]
Latvia and Brazil are excluded for lack of data, leaving 55 economies in the sample. Note that because of the limited availability of the other data used in the regressions (interest rates, housing prices, rent, etc) and the aggregation of multiple policy changes occurring within a quarter, this number is considerably smaller than the 662 individual policy actions in the policy database. [19]
To the extent that the lending rate is a longer-term interest rate, this finding is consistent with a large literature on the effects of the term spread on economic activity. [20]
This also reduces the number of economies included in the sample, since, in several cases, the relevant data series only begin in the mid 2000s. [21]
Serbia and Ukraine are dropped for lack of data, leaving 55 economies. [22]
These policies' applicability may be limited by the fact that it is typically difficult to change the tax code countercyclically in time for or to keep up with fast-changing market conditions. [23]
References
Ahearne A, J Ammer, B Doyle, L Kole and R Martin (2005), ‘House Prices and Monetary Policy: A Cross-Country Study’, Board of Governors of the Federal Reserve System International Finance Discussion Paper No 841.
Borio C and I Shim (2007), ‘What Can (Macro-)Prudential Policy do to Support Monetary Policy?’, BIS Working Paper No 242.
Borio C and H Zhu (2008), ‘Capital Regulation, Risk-Taking and Monetary Policy: A Missing Link in the Transmission Mechanism?’, BIS Working Paper No 268.
Calza A, T Monacelli and L Stracca (2009), ‘Housing Finance and Monetary Policy’, European Central Bank Working Paper No 1069.
Campbell JY (1991), ‘A Variance Decomposition for Stock Returns’, The Economic Journal, 101(405), pp 157–179.
Campbell SD, MA Davis, J Gallin and RF Martin (2009), ‘What Moves Housing Markets: A Variance Decomposition of the Rent-Price Ratio’, Journal of Urban Economics, 66(2), pp 90–102.
Claessens S, MA Kose and ME Terrones (2011), ‘Financial Cycles: What? How? When?’, IMF Working Paper No 11/76.
Crowe C, G Dell'Ariccia, D Igan and P Rabanal (2011), ‘How to Deal with Real Estate Booms: Lessons from Country Experiences’, IMF Working Paper No WP/11/91.
Cúrdia V and M Woodford (2010), ‘Credit Spreads and Monetary Policy’, Journal of Money, Credit and Banking, 42(supplement 1), pp 3–35.
Del Negro M and C Otrok (2007), ‘99 Luftballons: Monetary Policy and the House Price Boom across U.S. States’, Journal of Monetary Economics, 54(7), pp 1962–1985.
Dokko J, B Doyle, MT Kiley, J Kim, S Sherlund, J Sim and S Van den Heuvel (2009), ‘Monetary Policy and the Housing Bubble’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2009-49.
FSB-IMF-BIS (Financial Stability Board, International Monetary Fund and Bank for International Settlements) (2011), ‘Macroprudential Policy Tools and Frameworks: Progress Report to G20’, October.
Gallin J (2008), ‘The Long-Run Relationship Between House Prices and Rents’, Real Estate Economics, 36(4), pp 635–658.
Girouard N, M Kennedy, P van den Noord and C André (2006), ‘Recent House Price Developments: The Role of Fundamentals’, OECD Economics Department Working Paper No 475.
Glaeser EL, JD Gottlieb and J Gyourko (2010), ‘Can Cheap Credit Explain the Housing Boom?’, NBER Working Paper No 16230.
Glindro ET, T Subhanij, J Szeto and H Zhu (2008), ‘Determinants of House Prices in Nine Asia-Pacific Economies’, BIS Working Paper No 263.
Goodhart C and B Hofmann (2008), ‘House Prices, Money, Credit, and the Macroeconomy’, Oxford Review of Economic Policy, 24(1), pp 180–205.
Hilbers P, I Okter-Robe, C Pazarbasioglu and G Johnsen (2005), ‘Assessing and Managing Rapid Credit Growth and the Role of Supervisory and Prudential Policies’, IMF Working Paper No WP/05/151.
Himmelberg C, C Mayer and T Sinai (2005), ‘Assessing High House Prices: Bubbles, Fundamentals and Misperceptions’, The Journal of Economic Perspectives, 19(4), pp 67–92.
Iacoviello M and R Minetti (2003), ‘Financial Liberalization and the Sensitivity of House Prices to Monetary Policy: Theory and Evidence’, The Manchester School, 71(1), pp 20–34.
Igan D and H Kang (2011), ‘Do Loan-To-Value and Debt-To-Income Limits Work? Evidence from Korea’, IMF Working Paper No WP/11/297.
IMF (International Monetary Fund) (2011), ‘Housing Finance and Financial Stability – Back to Basics?’, Global Financial Stability Report: Durable Financial Stability: Getting There from Here, World Economic and Financial Surveys, IMF, Washington DC, pp 111–157.
Jarociński M and FR Smets (2008), ‘House Prices and the Stance of Monetary Policy’, Federal Reserve Bank of St. Louis Review, 90(4), pp 339–365.
Kuttner KN (2011), ‘Rent, Price, and User Cost in the U.S.: Do the Old Rules Still Apply?’, Williams College, unpublished manuscript.
Lim C, F Columba, A Costa, P Kongsamut, A Otani, M Saiyid, T Wezel and X Wu (2011), ‘Macroprudential Policy: What Instruments and How to Use Them? Lessons from Country Experiences’, IMF Working Paper No WP/11/238.
Mikhed V and P Zemčík (2007), ‘Testing for Bubbles in Housing Markets: A Panel Data Approach’, Center for Economic Research and Graduate Education – Economics Institute, CERGE-EI Working Paper No 338.
Poterba JM (1984), ‘Tax Subsidies to Owner-Occupied Housing: An Asset-Market Approach’, The Quarterly Journal of Economics, 99(4), pp 729–752.
Sá F, P Towbin and T Wieladek (2011), ‘Low Interest Rates and Housing Booms: The Role of Capital Inflows, Monetary Policy, and Financial Innovation’, Bank of England Working Paper No 411.
Sveriges Riksbank (2011), The Riksbank's Inquiry into the Risks in the Swedish Housing Market, April, Sveriges Riksbank, Stockholm.
Taylor JB (2007), ‘Housing and Monetary Policy’, in Housing, Housing Finance, and Monetary Policy, A Symposium sponsored by the Federal Reserve Bank of Kansas City, Kansas City, pp 463–476.
Taylor JB (2009), ‘The Financial Crisis and the Policy Responses: An Empirical Analysis of What Went Wrong’, NBER Working Paper No 14631.
Warnock VC and FE Warnock (2008), ‘Markets and Housing Finance’, Journal of Housing Economics, 17(3), pp 239–251.
Wong TC, T Fong, K-F Li and H Choi (2011), ‘Loan-To-Value Ratio as a Macro-Prudential Tool: Hong Kong's Experience and Cross-Country Evidence’, Hong Kong Monetary Authority Working Paper 01/2011.
Woodford M (2010), ‘Financial Intermediation and Macroeconomic Analysis’, The Journal of Economic Perspectives, 24(4), pp 21–44.
Wu J, J Gyourko and Y Deng (2010), ‘Evaluating Conditions in Major Chinese Housing Markets’, NBER Working Paper No 16189.