RBA Annual Conference – 2003 How Should Monetary Policy Respond to Asset-price Bubbles? David Gruen, Michael Plumb and Andrew Stone[1]
Abstract
We present a simple model of the macroeconomy that includes a role for an asset-price bubble, and derive optimal monetary policy settings for two policy-makers. The first policy-maker, a sceptic, does not attempt to forecast the future possible paths for the asset-price bubble when setting policy. The second policy-maker, an activist, takes into account the complete stochastic implications of the bubble when setting policy.
We examine the optimal policy recommendations of these two policy-makers across a range of plausible assumptions about the bubble. We show that the optimal monetary policy recommendations of the activist depend on the detailed stochastic properties of the bubble. There are some circumstances in which the activist clearly recommends tighter policy than that of the sceptic, while in other cases, the appropriate recommendation is to be looser than the sceptic. Other things equal, the case for ‘leaning against’ a bubble with monetary policy is stronger the lower the probability of the bubble bursting of its own accord, the larger the efficiency losses associated with big bubbles, and the higher the assumed impact of monetary policy on the bubble process.
1. Introduction
Asset-price bubbles pose difficult problems for monetary policy, and despite considerable debate no consensus has yet emerged on the appropriate strategy for monetary policy-makers in the presence of such bubbles.
Different views about the appropriate role of monetary policy in the presence of asset-price bubbles do not arise primarily because of differences about the objectives of monetary policy. These objectives, it is usually agreed, are to maintain low inflation and to limit the volatility of inflation and output, thereby contributing to stability in both the macroeconomy and the financial system. Rather, the different views are about how best to achieve these objectives.
One view is that monetary policy should do no more than follow the standard precepts of inflation targeting. Proponents of this view would acknowledge that rising asset prices often have expansionary effects on the economy, and might sometimes also provide a signal for incipient inflationary pressures, so that some tightening of monetary policy might be appropriate. According to this view, however, policy should only respond to observed changes in asset prices to the extent that they signal current or future changes to inflation or the output gap. There should be no attempt to use policy either to gently lean against a suspected asset-price bubble while it is growing or, more aggressively, to try to burst it. This view of the appropriate monetary policy response to asset-price bubbles has been put recently by Bernanke (2002).
An alternative view is that monetary policy should aim to do more than respond to actual and expected developments in inflation and the output gap. Cecchetti, Genberg and Wadhwani (2003), prominent proponents of this alternative view, put the argument in these terms:
… central banks seeking to smooth output and inflation fluctuations can improve… macroeconomic outcomes by setting interest rates with an eye toward asset prices in general, and misalignments in particular …Raising interest rates modestly as asset prices rise above what are estimated to be warranted levels, and lowering interest rates modestly when asset prices fall below warranted levels, will tend to offset the impact on output and inflation of [asset-price] bubbles, thereby enhancing overall macroeconomic stability. In addition, if it were known that monetary policy would act to ‘lean against the wind’ in this way, it might reduce the probability of bubbles arising at all, which would also be a contribution to greater macroeconomic stability. (p 429, italics added)[2]
We argue here that it is not clear that central banks should follow this advice. There is no universally optimal response to bubbles, and the case for responding to a particular asset-price bubble depends on the specific characteristics of the bubble process.
We present a simple model of the macroeconomy that includes a role for an asset-price bubble, and derive optimal monetary policy settings for two policy-makers. The first policy-maker, a sceptic, makes no attempt to forecast future movements in asset prices when setting policy, perhaps because she does not believe in the existence of the bubble or, alternatively, does not believe that monetary policy should actively respond to it. Her policy settings define the standard inflation-targeting benchmark in our model. The second policy-maker, an activist, takes into account the complete stochastic implications of the bubble when setting policy.
Once the bubble has formed, it is assumed to either grow each year with some probability, or to collapse and disappear. Crucially, and realistically, monetary policy in the model affects the economy with a lag, so that policy set today has its initial impact on the economy next year, by which time the bubble will have either grown further or collapsed.
For an activist policy-maker, it follows that there are two countervailing influences on monetary policy in the presence of the bubble. On the one hand, policy should be tighter than the standard inflation-targeting benchmark to counter the expansionary effects of future expected growth in the bubble and, in some formulations, to raise the probability that the bubble will burst. On the other hand, policy should be looser to prepare the economy for the possibility that the bubble may have burst by the time policy is having its impact on the economy.
Which of these two influences dominates? For intermediate and larger bubbles – which are of most importance to policy-makers – we argue that it depends on the characteristics of the bubble process. There are circumstances in which the activist should recommend tighter policy than the sceptic. This is likely to be the appropriate activist advice when one or more of the following conditions applies: the probability that the bubble will burst of its own accord over the next year is assessed to be small; the bubble's probability of bursting is quite interest-sensitive; efficiency losses associated with the bubble rise strongly with the bubble's size; or, the bubble's demise is expected to occur gradually over an extended period, rather than in a sudden bust.
Alternatively, however, when these conditions do not apply, it is more likely that the activist should recommend looser policy than the sceptic. This result makes clear that there is no single optimal rule for responding to all bubbles, and also illustrates the quite high level of knowledge of the future stochastic properties of the bubble that is required to set appropriate activist policy.
2. Model
Our model is an extension of the Ball (1999) model for a closed economy. In the Ball model, the economy is described by two equations:

where y is the output gap, r is the difference between the real interest rate and its neutral level, π is the difference between consumer-price inflation and its targeted rate, and α, β, and λ are positive constants (with λ <1 so that output gaps gradually return to zero).
The Ball model has the advantage of simplicity and intuitive appeal. It makes the simplifying assumption that policy-makers control the real interest rate, rather than the nominal one. It assumes, realistically, that monetary policy affects real output, and hence the output gap, with a lag, and that the output gap affects inflation with a further lag. The values for the parameters α, β, and λ that Ball chooses for the model, and that we will also use here, imply that each period in the model is a year in length.[3]
We augment the model with an asset-price bubble. We assume that in year 0, the economy is in equilibrium, with both output and inflation at their target values, y0 = π0 = 0, and that the bubble has zero size, a0 = 0. In subsequent years, we assume that the bubble evolves as follows:
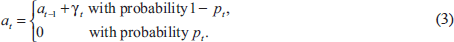
Thus, in each year, the bubble either grows by an amount, γt > 0, or bursts and collapses back to zero. For ease of exposition, in the rest of this section we will assume that γt is constant, γt = γ, but we will allow for a range of alternative possibilities in the results we report in the next section. We also assume that once the bubble has burst, it does not re-form. To allow for the effect of the bubble on the economy, we modify Ball's two-equation model to read:

In each year that the bubble is growing it has an expansionary effect on the economy, increasing the level of output, and the output gap, by γ. The bubble is, however, assumed to have no direct effect on consumer price inflation, although there will be consequences for inflation to the extent that the bubble leads the economy to operate with excess demand as it expands, and with excess supply when it bursts.
When the bubble bursts, the effect on the economy is of course contractionary – if the bubble bursts in year t, the direct effect on output, and the output gap, in that year will be Δat = −(t − 1)γ. Thus, the longer the bubble survives, the greater will be the contractionary effect on the economy when it bursts.
We will assume that the evolution of the economy can be described by this simple three-equation system (Equations (3), (4) and (5)). But we distinguish between two policy-makers: a sceptic who doesn't try to second-guess asset-price developments, and an activist who believes that she understands enough about asset-price bubbles to set policy actively in response to them.[4]
We assume that the policy-makers observe in each year whether the bubble has grown further, or collapsed, before setting the interest rate for that year. Given the nature of the lags in the model, this year's interest rate will have no impact on real activity until next year, and on inflation until the year after that.
We also assume that the two policy-makers have the same preferences, and that they care about the volatility of both inflation and output. Thus we assume that in each year t, policy-maker p (activist or sceptic) sets the real interest rate, rt, to minimise the weighted sum of the expected future squared deviations of inflation and output from their target levels, or in symbols, sets rt to minimise

where μ is the relative weight on the deviations of inflation and 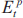 is the year t expectation of policy-maker
p. In the results we show in the paper, we set μ = 1,
so that policy-makers are assumed to care equally about deviations of inflation
from target and output from potential.
is the year t expectation of policy-maker
p. In the results we show in the paper, we set μ = 1,
so that policy-makers are assumed to care equally about deviations of inflation
from target and output from potential.
In setting policy each year, the sceptical policy-maker ignores the future stochastic behaviour of the bubble. Since certainty equivalence holds in the model in this setting, Ball shows that, for the assumed parameter values, optimal policy takes the form

which is a more aggressive Taylor rule than the ‘standard’ Taylor rule introduced by Taylor (1993), rt = 0.5yt+0.5πt.
As the bubble grows, the sceptical policy-maker raises the real interest rate to offset the bubble's expansionary effects on the economy. But she does so in an entirely reactive manner, ignoring any details about the bubble's future evolution. Once the bubble bursts, output falls precipitously and the sceptical policy-maker eases aggressively, again in line with the dictates of the optimal policy rule, Equation (7).[5]
We assume that the activist policy-maker learns about the bubble in year 0, and hence takes the full stochastic nature of the bubble into account when setting the policy rate, rt, from year 0 onwards. Once the bubble bursts, however, there is no further uncertainty in the model, and the activist policy-maker simply follows the modified Taylor rule, Equation (7), just like the sceptical policy-maker.
3. Results
In this section, we present optimal policy recommendations through time, assuming that the bubble survives and grows. We focus on the growth phase of the bubble's life because it is of most policy interest, as it generates the most disagreement about which policy approach is preferable. Once the bubble bursts, by contrast, there is general agreement that it is appropriate to ease aggressively to offset the contractionary effects of the bust.[6]
Our main aim is to compare the optimal policy recommendations of the sceptic with those of an activist, over a range of plausible alternative assumptions about the stochastic nature of the bubble. To do so in a meaningful way, it is necessary that the two policy-makers face an economy in the same state in each year. Since the current state of the economy depends on previous policy settings (as well as on the evolution of the bubble) we will assume throughout that the policy settings that are actually implemented each year are those chosen by the sceptic.
We can then meaningfully ask each year: given the state of the economy, what are the current optimal policy recommendations made by the different policy-makers? The activist's recommendations will depend on the assumptions she makes about the future possible paths of the bubble, while the sceptic's will not, since she assumes that future asset-price shocks have no expected effects.
3.1 Baseline results: policy cannot affect the bubble
We begin with some simple baseline results. For these results, we assume that the bubble's direct expansionary effect on output in each year of its growth is a constant 1 per cent (i.e., γt = 1). Figure 1 shows the optimal policy choices made by the sceptic and two activists. We focus first on the sceptic, and then on the activists.
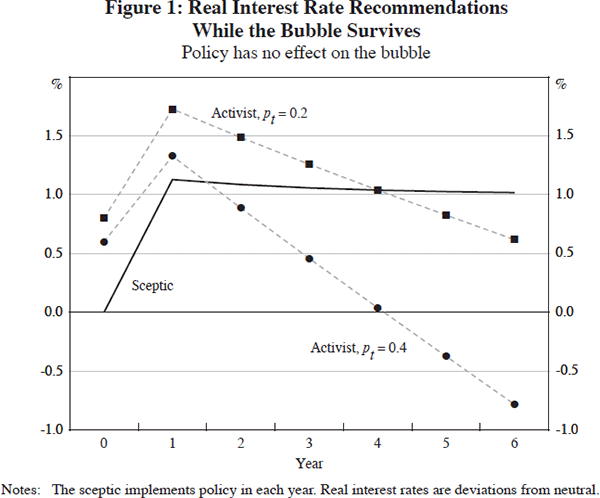
Since the sceptic assumes that future asset-price shocks have no expected effects, she responds to the bubble only when its initial expansionary effects are manifest in year 1. As time proceeds and the bubble grows, she sets the policy interest rate in line with Equation (7), which is optimal given her beliefs about future asset-price shocks. Of course, were the bubble to burst, she would ease immediately (see Appendix A for further details).
An activist, deciding on optimal policy in year t, understands that if the bubble continues to grow, its direct effect on output next year will be +1 per cent, while if it bursts, the direct effect next year will be – at per cent. If the probability of bursting each year is a constant, p*, the bubble's expected direct effect on output next year is (1−p*)−p*at.
Certainty equivalence applies to this baseline version of the
model.[7]
It follows that the difference between the policy interest rates recommended by the
activist, 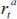 , and the sceptic,
, and the sceptic, 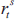 , depends only on their different assessments of
the expected effect of the bubble on output next year. With the sceptic assuming
that the bubble will have no expected effect on output next year, it follows
that
, depends only on their different assessments of
the expected effect of the bubble on output next year. With the sceptic assuming
that the bubble will have no expected effect on output next year, it follows
that

Equation (8) implies that the activist will recommend tighter (easier) policy than the sceptic whenever, in probability-weighted terms, the expansionary effect on real activity from the bubble surviving is greater (less) than the contractionary effect from the bubble collapsing.
For the results shown in Figure 1, we assume that the only difference between the two activists is that one assesses the probability that the bubble will burst each year as pt = p* = 0.2 (the ‘durable-bubble activist’), while the other assesses it as pt = p* = 0.4 (the ‘transient-bubble activist’).[8]
In terms of their optimal policy recommendations, the two activists agree that policy should be tighter than the settings chosen by the sceptic for the first couple of years of the bubble's growth (including year 0, since that is when they learn about the bubble). Although they disagree about the details, they share the assessment that the continued probable growth of the bubble is a more important consideration for policy than the bubble's possible collapse.
The activists both understand, however, that as time proceeds, the bubble is getting bigger and the size of the prospective bust is also getting bigger. As a consequence, if the bubble survives for more than a year or two, the two activists no longer agree about whether policy should be tighter or looser than the modified Taylor-rule settings chosen by the sceptic. The durable-bubble activist recommends tighter policy because she assesses the probability of the bubble bursting to be small, but the transient-bubble activist recommends looser policy because her assessment is that this probability is larger.
If the bubble survives for long enough the two activists will again concur at least in the direction of their policy advice – they will both recommend looser policy than the sceptic because the possibility of the by-now-bigger bubble collapsing eventually dominates for them both.
In this case, then, the policy recommendations of an activist — and even whether she recommends tighter or looser policy than the benchmark settings chosen by the sceptic — depend crucially on her assessment of the probability that the bubble will collapse of its own accord. This is an important example of the general point that the activist's policy advice will depend critically on the detailed assumptions she makes about the stochastic properties of the bubble. This is the central insight of the paper. We now show the relevance of this insight across a wide range of alternative assumptions about the bubble's stochastic behaviour.
3.2 Sensitivity analysis[9]
3.2.1 Policy affects the probability that the bubble will burst
An obvious extension to the model is to assume that by setting tighter policy this year, the policy-maker can raise the probability that the bubble will burst next year. For simplicity, we initially assume a linear relationship between the interest rate and the probability of the bubble bursting:

We assume that δ = 0.1, so that a 1 percentage point rise in the real interest
rate this year raises the probability of the bubble bursting next year by 0.1,
subject to the constraint that 0 ≤ pt ≤ 1. The path
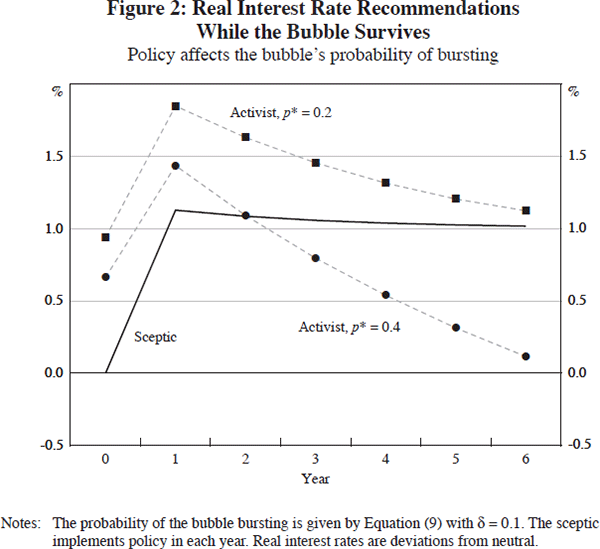
of interest rates, 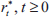 , is the optimal path chosen by the sceptical
policy-maker.[10]
, is the optimal path chosen by the sceptical
policy-maker.[10]
As before, we assume that the bubble's direct expansionary effect on output in each year of its growth is a constant 1 per cent (i.e., γt = 1). Figure 2 shows the optimal policy recommendations made by the sceptic and two activists. The two activists again differ only in their assessment of the bubble's probability of collapse. Both believe that this probability is given by Equation (9), but the durable-bubble activist believes that p* = 0.2, while the transient-bubble activist believes that p* = 0.4.
The sceptic's optimal policy profile is the same as in Figure 1, because she ignores the future stochastic details of the bubble. By contrast, it is optimal for the activists to recommend tighter policy than they would recommend if they had no influence on the bubble, as can be seen by comparing the activist profiles in Figures 1 and 2. By tightening somewhat, the activists reduce the probability that the bubble will grow further and be more disruptive to the economy when it ultimately bursts. Nevertheless, the optimal policy continues to depend, sensitively, on the activist's assessment of the bubble's probability of collapse, just as it did when the activists could not affect the bubble.
It is also of interest to see how the results change when we vary the sensitivity to interest rates of the bubble's probability of collapse. For this exercise, we assume a monotonically increasing, but non-linear, relationship between interest rates and this probability, to avoid a corner-solution problem with the linear form (explained shortly). The relationship we assume is:

where a = −δ/[p*(1−p*)]
and b = ln/[(1−p*)/p*].
For this functional form, pt = p* when
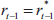 and
and 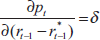 when this derivative is evaluated at
when this derivative is evaluated at 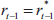 These two features are also features of the linear
form, Equation (9). The advantage of the non-linear form, Equation (10), is
that, while raising last year's interest rate, rt−1,
raises the probability that the bubble will burst this year, pt,
it cannot drive that probability to 1, as can occur with the linear
form.[11]
These two features are also features of the linear
form, Equation (9). The advantage of the non-linear form, Equation (10), is
that, while raising last year's interest rate, rt−1,
raises the probability that the bubble will burst this year, pt,
it cannot drive that probability to 1, as can occur with the linear
form.[11]
Figure 3 shows a comparison of optimal interest rate recommendations for the sceptic and three activists. The activists assume that the bubble's probability of bursting is given by Equation (10) with p* = 0.4 (except p14 = 1), but they assume three different degrees of interest-rate sensitivity: δ = 0.1, δ = 0.2 or δ = 0.3.
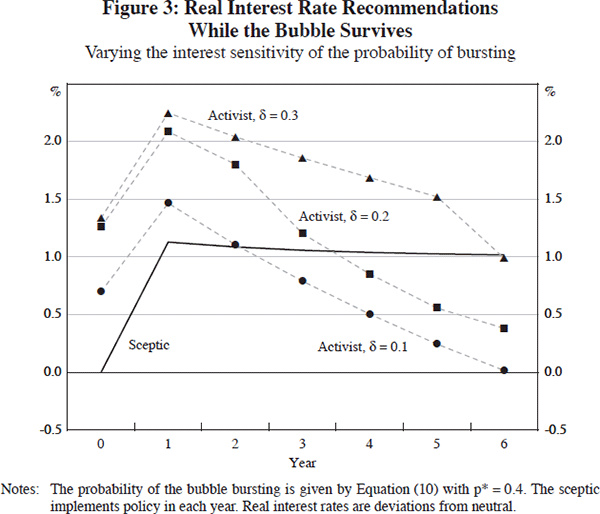
The pattern of optimal interest rate recommendations is somewhat similar to those in Figures 1 and 2. When the bubble is very small, the activists all agree that policy should be tighter than the setting chosen by the sceptic. But this consensus among the activists evaporates as the bubble gets bigger, and from year 2 onward, first one and then two of the three activists recommend looser policy than the sceptic, while the activist who believes that the bubble is highly interest-sensitive (δ = 0.3) continues to recommend tighter policy, at least until year 6.
3.2.2 Allowing for efficiency losses
A second natural extension is to allow for efficiency losses associated with the bubble. There are two broad ways to motivate the idea of efficiency losses. They can be motivated in terms of the economically inefficient physical over-investment that is put in place in response to asset-price rises that are not based on fundamentals, or in terms of the damage done to the financial system when the bubble bursts.
Either way, it seems plausible that the efficiency losses rise with the size of the bubble. To account for these losses, we re-formulate the policy problem as setting rt to minimise
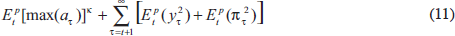
where we assume that the efficiency losses rise either linearly with the maximum
size of the bubble (κ = 1) or with the square of this maximum size (quadratic
case, κ = 2). We also assume, as before, that the relative weight on
inflation deviations, µ, takes a value of one. Since the sceptic ignores the bubble,
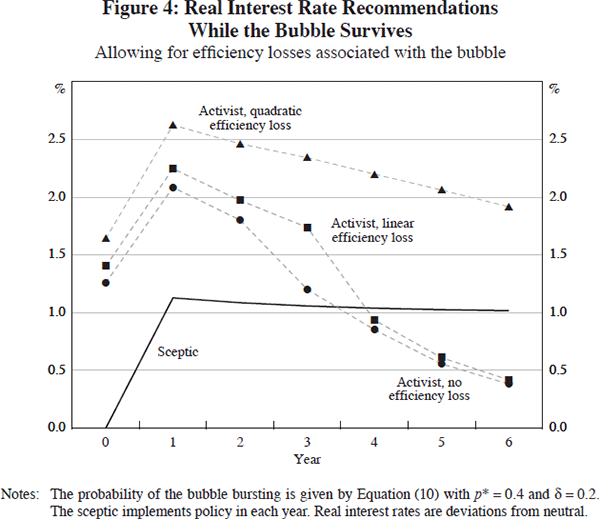
we assume for her that 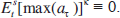
Figure 4 shows a comparison of optimal interest rate recommendations for the sceptic and three activists. The activists all assume that the bubble's probability of bursting is given by Equation (10) with p* = 0.4, and with interest-rate sensitivity, δ = 0.2. The first activist, however, makes no allowance for efficiency losses, and hence minimises the standard loss function, Equation (6). The second activist assumes linear efficiency losses, while the third assumes quadratic losses, and so they minimise the loss function, Equation (11), assuming appropriate values for κ.
As previous figures have shown, being able to raise the probability of the bubble bursting gives an incentive to the activist policy-maker to tighten policy somewhat. Figure 4 shows that taking account of efficiency losses associated with an asset-price bubble raises this incentive further, and therefore further raises the optimal interest rate recommendations of the activist. Moreover, if efficiency losses associated with the bubble are assumed to rise sufficiently rapidly with the maximum size of the bubble, then the incentive for the activist to recommend tighter policy than the sceptic is a strong one.
3.2.3 Policy affects the bubble's growth
A further natural extension to the simple version of the model involves assuming that, rather than affecting the probability of the bubble bursting, the activist policy-maker can, by setting tighter policy this year, reduce the extent of the bubble's growth next year if it survives. For the simulations we show for this case, we assume that pt = p* = 0.4 (except p14 = 1) and that

For reasons we discuss shortly, only large values of the parameter φ generate
significantly changed behaviour by the activist policy-maker. We therefore
assume that φ = 1, so that by setting policy 1 percentage point higher
than the sceptic this year, the bubble's growth next year is reduced from
1 per cent to
nothing.[12]
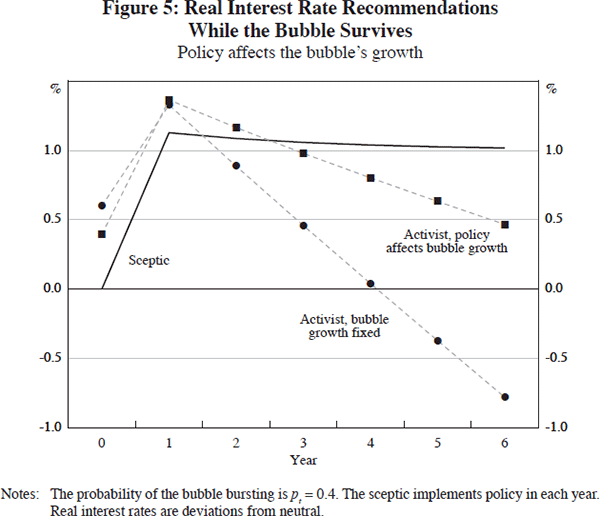
As above, the path of interest rates defined by 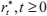 , is the optimal path chosen by the sceptical policy-maker
assuming γt = 1.
, is the optimal path chosen by the sceptical policy-maker
assuming γt = 1.
Figure 5 shows a comparison of optimal interest rate recommendations for the sceptic and two activists. Both activists assume that the bubble's growth is given by Equation (12), but one assumes no interest-rate sensitivity, φ = 0, while the other assumes high sensitivity, φ = 1.[13]
For every year apart from year 0, being able to reduce the bubble's growth induces the activist policy-maker to recommend tighter policy than she otherwise would. The differences in the policy recommendations induced by this expectation are, however, less pronounced than the differences that arise when an activist policy-maker assesses the probability that the bubble will burst each year at pt = 0.2 rather than pt = 0.4, as can be seen by comparing Figures 1 and 5.
3.2.4 Bubbles that take two or more years to collapse
Another extension to the basic model involves assuming that, when the bubble collapses, it does so evenly over two or more years, rather than suddenly in one. In the examples we have examined until now, the activist must always confront the problem that, owing to the lag structure of the Ball model, policy can only respond to a collapsing bubble after the collapse is complete. This problem is reduced by assuming that the collapse occurs over two or more years rather than one.
Figure 6 shows results for the sceptic and two activists (one who assumes gradual, even, two-year collapse; the other, sudden), assuming that pt = p* = 0.4 (except p14 = 1) and that γt = 1. The activist who assumes that the bubble will collapse only gradually recommends tighter policy than the one who assumes that it will be sudden, because of their different assessments of the bubble's expected effect on next year's output.
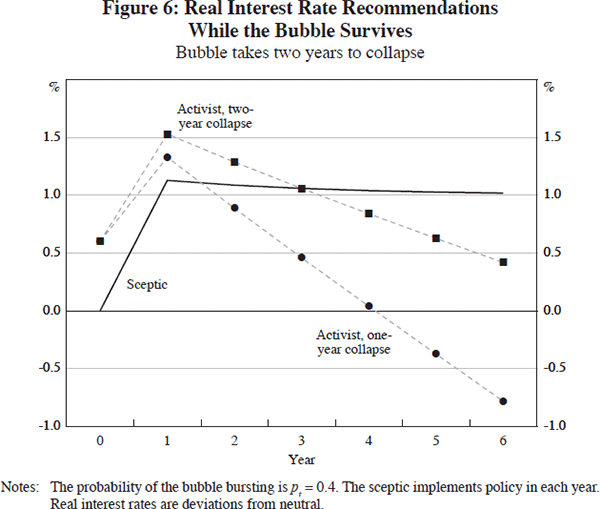
Nevertheless, the overall pattern of policy recommendations remains similar to earlier cases. As the size of the bubble grows, the ‘gradually-bursting’ activist eventually recommends looser policy than the sceptic does, for reasons that are by now familiar.
In cases in which the bubble is expected to collapse evenly over three or more years, the activist would recommend tighter policy than the sceptic for longer, while the bubble is growing, a result that follows from a straightforward extension to Equation (8).
3.2.5 A rational bubble
In the baseline results presented at the beginning of the section, we assumed that the asset-price bubble grew at a uniform rate, γt = 1, and that the probability of the bubble's collapse was constant through time. This seems to us a simple and intuitively appealing baseline case.
In this case, however, there is no arbitrage condition ruling out unexploited profit opportunities in the assets whose price rises constitute the bubble. Our baseline case is therefore not a ‘rational’ bubble. We do not see this as a shortcoming — to our minds, there is much evidence that the asset-price bubbles we see in modern industrial economies are not rational in this sense (see, for example, Shiller (2000)). Nevertheless, it is of interest to derive results for the case of a rational bubble.
Such a bubble arises from the actions of a rational investor who buys the relevant assets up to the point at which expected profits are driven to zero.[14] If the probability of collapse is constant, p*, and the capital gain to the investor in year t+1 if the bubble collapses is −at , then a rational risk-neutral investor will be indifferent to holding the asset when the expected growth of the bubble, if it survives, is Δat+1 = atp*/(1−p*). This is a geometrically growing bubble, rather than the constant-growth bubble that constituted our baseline case.[15]
The arbitrage condition that defines this rational bubble implies that the bubble's
expected growth over the next year, 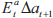 , is zero. In this case, however, the activist and
the sceptic are making identical assumptions about the bubble's expected
effect on next year's output. It follows that the activist will always
recommend the same policy interest rate as the sceptic for a rational bubble,
provided she believes that the stochastic properties of the bubble are not
affected by the actions of policy-makers, so that certainty equivalence
holds.[16]
, is zero. In this case, however, the activist and
the sceptic are making identical assumptions about the bubble's expected
effect on next year's output. It follows that the activist will always
recommend the same policy interest rate as the sceptic for a rational bubble,
provided she believes that the stochastic properties of the bubble are not
affected by the actions of policy-makers, so that certainty equivalence
holds.[16]
4. Discussion and Conclusions
Table 1 provides a summary of the results. For each set of assumptions, it shows, as time proceeds and the bubble grows, whether the activist would recommend tighter (+), looser (−) or the same (=) policy settings as the sceptic.
| Scenario | Year 1 | Year 2 | Year 3 | Year 4 | Year 5 | Year 6 |
|---|---|---|---|---|---|---|
| Policy can't affect bubble | ||||||
| pt = 0.2 | + | + | + | = | – | – |
| pt = 0.4 | + | – | – | – | – | – |
| Policy affects probability of bursting | ||||||
| p* = 0.2, δ = 0.1 | + | + | + | + | + | + |
| p* = 0.4, δ = 0.1 | + | + | – | – | – | – |
| p* = 0.4, δ = 0.2 | + | + | + | – | – | – |
| p* = 0.4, δ = 0.3 | + | + | + | + | + | – |
| Linear efficiency losses | + | + | + | – | – | – |
| Quadratic efficiency losses | + | + | + | + | + | + |
| Policy affects bubble growth | + | + | – | – | – | – |
| Bubble bursts over two periods | + | + | + | – | – | – |
| Rational bubble | = | = | = | = | = | = |
There are several broad lessons worth highlighting from this summary. When the asset-price bubble is small enough, the activist policy-maker always (except in the case of the rational bubble) recommends tighter policy than the sceptic who ignores the future possible paths of the bubble. However, this result is of limited practical relevance. Although we have assumed that activist policy-makers learn about the nature of the bubble at its inception, in reality there is likely to be much doubt in the early stages about whether rising asset prices constitute a bubble. Asset-price bubbles rarely arise out of thin air — instead, they usually occur when the evolving economic fundamentals are consistent with some rise in asset prices. While there will always be some doubt about whether rising asset prices constitute a bubble, these doubts would seem particularly acute when the suspected deviation of asset prices from fundamentals remains small and has been short-lived. For these reasons, there would seem to be no strong case for central banks to respond to small asset-price misalignments.[17]
As the bubble grows, however, there are two developments with potentially conflicting implications for appropriate activist policy. On the one hand, an activist policy-maker should become increasingly confident that the observed asset-price rises do constitute a bubble, which should strengthen the case for responding actively to them. On the other hand, as the bubble grows, the potential negative effects from its eventual bursting will increase. Whether this constitutes an argument for tighter or looser policy will depend on the nature of the bubble.
The case for tightening is to offset the expansionary effects of future expected growth of the bubble and, in some formulations, to reduce the bubble's growth or help to burst it. As we have seen, there are circumstances in which this case is particularly compelling, in particular when: the probability that the bubble will burst of its own accord over the next year is assessed to be small; the bubble's probability of bursting is quite interest sensitive; efficiency losses associated with the bubble rise strongly with the bubble's size; or, the bubble's demise is expected to occur gradually over an extended period, rather than in a sudden bust. Conversely, the case for loosening is strongest when these conditions are reversed, since in those circumstances it becomes increasingly important to allow for the contractionary impact that arises when the bubble bursts.[18] The stochastic process driving the bubble is thus crucial to determining which of these considerations predominates.[19]
Ultimately, the appropriate policy strategy is a matter for judgement. Since the optimal policy response at any point depends on the stochastic properties of the bubble, our results highlight the information requirements inherent in an activist approach. Where sufficient information about the bubble process is not available to the policy-maker, a robust approach, something along the lines of the one used by our sceptic, may be the best that can be achieved. Given sufficient information about the bubble process an activist approach may be feasible, but our results suggest that the appropriate response to bubbles is not uniform. In particular, it may be optimal to ‘lean against’ some bubbles but not others, and hence the formulation of an activist strategy requires judgments to be made about the process driving the bubble and its likely sensitivity to monetary policy.
Appendix A: Policy Settings for a Bubble that Bursts in the Fifth Year
We assume a constant probability pt = 0.2 that the bubble bursts in each year. In contrast to the simulations reported in the text, we allow both the sceptic and the activist to implement policy through time — so that the state of the economy depends on the identity of the policy-maker. Figure A1 shows results assuming that, as events turn out, the bubble grows for four years, during which time it has a direct expansionary effect on output of γ = 1 per cent in each year, and then bursts in the fifth year, with a direct contractionary effect on output of 4 per cent in that year.[20] The top panel shows the real interest rate profiles, rt, set by the two policy-makers; the second and third panels show the outcomes for the output gap, yt, and the inflation rate, πt.
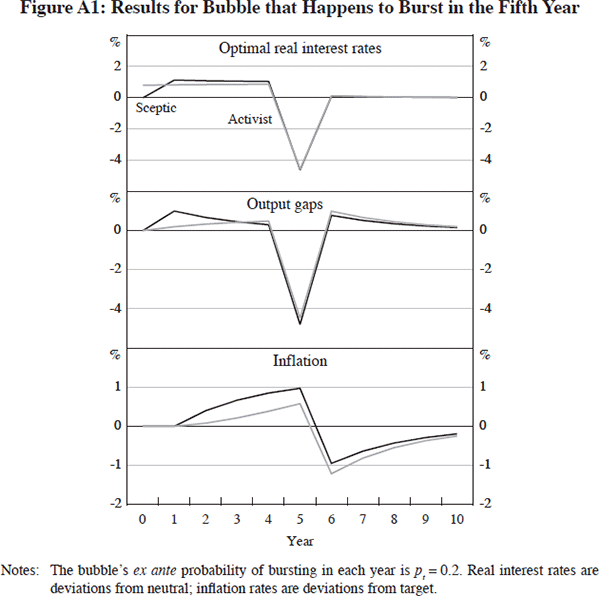
While the bubble is growing, the paths for output and inflation generated by the sceptic's policy settings reflect the continued expansionary effects of the bubble. The activist responds more aggressively to these expansionary effects because she anticipates them, but nevertheless she does not offset them completely because of the possibility that the bubble may be about to burst. Therefore, even with the activist's optimal policy settings, output and inflation remain above target while the bubble survives.
The bursting of the bubble in year 5 generates a severe recession. Output falls by more than the direct contractionary effect of the bubble bursting, because policy in the previous year has been tighter than neutral to offset the bubble's expansionary effects. In response to the bubble's collapse, policy is eased aggressively. Despite using the same policy rule after the bubble bursts, the modified Taylor rule, Equation (7), the paths for the policy interest rate, output, and inflation are somewhat different for the two policy-makers because they have set different policy interest rates in earlier years.
Appendix B: Comparison with Kent and Lowe (1997)
Kent and Lowe (1997) present a simple model of an asset-price bubble that has similarities with ours. They derive optimal activist policy in their model for two of the cases we have examined: when the probability of the bubble collapsing is exogenous, and when this probability rises with the previous period's policy interest rate.[21]
Kent and Lowe show that, when policy cannot affect the bubble's probability of collapse, optimal activist policy generates average inflation in their period 2 equal to the central bank's target rate of inflation. When policy can affect the bubble's probability of collapse, however, optimal activist policy generates average inflation in period 2 less than the central bank's target rate of inflation (where the averages are calculated over all possible outcomes for the bubble).
The qualitative nature of these results carries over to our model set-up. When policy cannot affect the bubble, average inflation in every year of our model is also equal to the central bank's target. When policy can affect the bubble, however, either by affecting its probability of bursting or its rate of growth, average inflation from year 2 onward is always less than the central bank's target when activist policy is implemented.[22]
Kent and Lowe use their model to make the case that, when policy can affect the bubble's probability of collapse, it may make sense for the policy-maker to raise interest rates early in the life of the bubble, even though this will increase the likelihood of inflation being below target in the near term. As we have seen, this general case — for tightening policy early in the life of the bubble — survives in our model. What our model adds to this story is that ‘early in the life of the bubble’ may not last very long. For many of our simulations, within a couple of years or so of the bubble's inception, it is no longer clear whether optimal activist policy should be tighter or looser than the policy chosen by a sceptic.
Footnotes
Macroeconomic Group, Australian Treasury (D Gruen) and Economic Group, Reserve Bank of Australia (M Plumb and A Stone). We are grateful to Glenn Stevens for a conversation that initiated this work, and to Guy Debelle, Malcolm Edey, Philip Lowe, Andrew Rose and Dave Stockton for helpful suggestions. The views expressed in this paper are those of the authors and should not be attributed to their employers. [1]
Cecchetti et al are careful to argue that monetary policy should not target asset prices. To quote them again, ‘we are not advocating that asset prices should be targets for monetary policy, neither in the conventional sense that they belong in the objective function of the central bank, nor in the sense that they should be included in the inflation measure targeted by monetary authorities’ (p 429, italics in the original). [2]
Ball's parameter values are α = 0.4, β = 1 and λ = 0.8. Ball also adds white-noise shocks to each of his equations, which we have suppressed for simplicity. [3]
To draw the distinction more precisely, both policy-makers understand how the output gap and inflation evolve over time, as summarised by Equations (4) and (5). The activist also understands, and responds optimally to, the stochastic behaviour of the bubble, as summarised by Equation (3). The sceptic, by contrast, responds to asset-bubble shocks, Δat , when they arrive, but assumes that the expected value of future shocks is zero. [4]
We implicitly assume that the zero lower bound on nominal interest rates is not breached when policy is eased after the bubble bursts, so that the real interest rate can be set as low as required by Equation (7). [5]
For completeness, Appendix A shows optimal interest rate recommendations both before and after the bursting of the bubble. [6]
The model set-up is more complex than the standard set-up in which certainty equivalence
applies. This is because, once the bubble bursts, there are no further asset-bubble
shocks and hence, ex ante, the distribution of shocks is
not independent through time. It is therefore not straightforward to demonstrate
certainty equivalence. Nevertheless, Equation (8) in the text does follow
and can be generalised to allow for alternative parameter values, time-varying
bubble growth and/or probabilities of bubble collapse, provided that the
evolution of the bubble remains independent of the actions of the policy-makers.
The generalised equation is 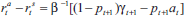 which, in particular, implies that
which, in particular, implies that 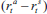 does not depend on α, λ or μ.
A proof of this equation is available from the authors on request.
[7]
does not depend on α, λ or μ.
A proof of this equation is available from the authors on request.
[7]
Assuming pt = 0.2 implies an average remaining life for the bubble of five years, while pt = 0.4 implies an average remaining life of two and a half years. [8]
Most of the extensions we examine in this section imply that certainty equivalence no longer applies to the model (the exceptions are the bubble that collapses over two or more years and the rational bubble), in which case the results must be derived by numerical optimisation. To simplify the numerical problems, we assume that if the bubble survives until year 14 (which is a very unlikely event for all the parameter values we consider) then it bursts with certainty in that year. For earlier years, this assumption is only relevant for the policy choices of the activist policy-maker. [9]
We choose the functional form in Equation (9) so that, for the benchmark policy settings chosen by the sceptic, pt = p* for all t. The results generated using an alternative functional form, pt = p* + δ rt−1, are qualitatively very similar to those shown. [10]
It seems implausible that moderate rises in the real interest rate would burst the bubble with certainty; yet that is an implication of the linear form, Equation (9). Simulations of the linear model with δ > 0.1 do indeed generate this outcome (results not shown). It is for this reason that we use the non-linear form for simulations with δ > 0.1. As argued by Dave Stockton in his comments on this paper, one could also imagine that the relationship between the bubble's probability of collapse and the policy interest rate might be non-monotonic, with small interest-rate rises lowering the subsequent probability of collapse. This would undoubtedly further complicate the optimal policy recommendations of an activist. [11]
If the bubble survives, it would again be necessary to set policy 1 percentage point higher than the sceptic to ensure that the bubble did not grow in the subsequent year. Given the effects of continually tight policy on the rest of the economy, it is perhaps not surprising that being able to raise the probability that the bubble will burst has more influence on optimal policy than simply being able to reduce its growth each year by setting tighter policy in each previous year. [12]
The results assuming no interest-rate sensitivity are equivalent to the baseline results shown in Figure 1 for the activist assuming pt = 0.4. [13]
We assume that the assets yield an annual return equal to the real interest rate, so that the expected profit relative to holding 1-year government bonds is determined by the expected capital gain on the assets. [14]
Note that, if the probability of collapse is not constant, a rational bubble need not grow at a constant geometrical rate. [15]
This result relies on a number of implicit, simplifying assumptions about the economy. In particular, it relies on the assumptions that the effect on the output gap of changes in asset prices is proportional to the size of those changes, and that rational investors and the activist policy-maker agree on the exact stochastic details of the bubble. Relaxing either of these assumptions could generate different policy recommendations by the activist. For example, for a geometrically growing bubble, it could account for an activist policy-maker assessing the bubble's growth rate to be faster (slower) than ‘rational’ — say, Δat+1 = Χatp*/(1−p*), with Χ > 1 (Χ < 1) — in which case the activist's policy recommendations would always be tighter (looser) than the sceptic's, for as long as the bubble survived. [16]
Cecchetti et al (2003, p 440) also make this point when they say ‘our proposal [to raise interest rates modestly as asset prices rise above what are estimated to be warranted levels] does not call for central banks to respond to small misalignments. We agree that these are difficult to detect and are unlikely to have very strong destabilising effects in any case’. [17]
In a passage immediately following the one quoted in the previous footnote, Cecchetti et al say ‘… there are clearly times when egregious misalignments exist. Recent examples include Japanese stock and land prices in 1989, and the NASDAQ in late 1999 and early 2000. While some portion of these high price levels may have been justifiable based on fundamentals, few people would deny that a significant component was due to asset market disturbances. Ultimately, in terms of reducing inflation and output volatility, it is important that central bankers respond to these large relatively “obvious” misalignments’. (2003, p 440, italics added) When misalignments are large and relatively obvious, however, our results suggest that it may be unclear whether the appropriate policy response should be to raise interest rates modestly or to lower them, unless the policy-maker is able to make use of specific knowledge about the stochastic process driving the bubble. [18]
It is also possible that the probability of the bubble bursting of its own accord over the next year might rise as the bubble gets larger. If so, the case for looser, rather than tighter, policy by the activist is further strengthened, a point also made by Kent and Lowe (1997) (see Appendix B). For most of our simulations, we have assumed p* = 0.4, implying an average remaining life for the bubble of two and a half years, which may be a more plausible assumption for intermediate and larger bubbles than p* = 0.2, which implies an average remaining life of five years. [19]
A bubble with a probability of bursting each year of pt = 0.2 bursts on average in the fifth year. [20]
Theirs is a three-period model in which the bubble, which has formed in period 1, can either grow or collapse back to zero in period 2, and if it has grown, can grow further or collapse in period 3. Their periods should therefore probably be thought of as spanning more than one year. [21]
Recall that it takes two years for policy changes to affect inflation in our model. As for the Kent and Lowe model, in each year the averages must be calculated over all possible outcomes for the bubble, weighted by their appropriate probabilities. Calculated in this way, the averages are therefore equivalent to period-0 expectations. [22]
References
Ball L (1999), ‘Efficient rules for monetary policy’, International Finance, 2(1), pp 63–83.
Bernanke BS (2002), ‘Asset-price “bubbles” and monetary policy’, remarks before the New York Chapter of the National Association for Business Economics, New York, 15 October. Available at <http://www.federalreserve.gov/boarddocs/speeches/2002/20021015/default.htm>.
Cecchetti SG, H Genberg and S Wadhwani (2003), ‘Asset prices in a flexible inflation targeting framework’, in WC Hunter, GG Kaufman and M Pomerleano (eds), Asset price bubbles: the implications for monetary, regulatory, and international policies, MIT Press, Cambridge, Mass, pp 427–444.
Kent C and P Lowe (1997), ‘Asset-price bubbles and monetary policy’, Reserve Bank of Australia Research Discussion Paper No 9709.
Shiller RJ (2000), Irrational exuberance, Princeton University Press, Princeton.
Taylor J (1993), ‘Discretion versus policy rules in practice’, Carnegie-Rochester Conference Series on Public Policy, 39, pp 195–214.