RBA Annual Conference – 1997 Financial-asset Prices and Monetary Policy: Theory and Evidence Frank Smets[*]
1. Introduction
The monetary-policy environment over the past decade in industrial countries has been increasingly characterised by low and stable inflation and often large movements in the prices of equities, bonds and foreign exchange, or financial assets more broadly. While volatility in part reflects the nature of asset prices, driven primarily by revisions in expectations of future returns, large movements raise questions about the appropriate response of monetary policy. In the past year, for instance, several central banks have expressed concern about such changes. In the United States, Chairman Greenspan raised questions about the large gains in stock prices and whether they had extended beyond levels that are justifiable on the basis of economic fundamentals. In many formerly high-yielding bond markets such as in Italy and Spain, yields fell by several percentage points, often putting pressure on the respective central banks to relax policy rates. In the United Kingdom, the pound sterling appreciated by more than 15 per cent in effective terms from August 1996 to the beginning of 1997, giving rise to a lively debate between market observers and the central bank about the appropriate policy response.
The first part of this paper (Section 2) attempts to put these concerns in perspective by putting forward a common framework in which the optimal policy response to financial-asset prices can be analysed. Within the context of the central bank's objective of price stability, the basic answer to the question raised is simple: the central bank's response to unexpected changes in asset prices should depend on how these changes affect the inflation outlook; if they imply a rise in the inflation forecast, policy should tighten and vice versa.[1]
The harder task is to determine how the inflation forecast is affected, as this requires a structural model of the economy. Although the model developed in Section 2.1 following Gerlach and Smets (1996) is simple, it does highlight two reasons why unexpected asset-price movements may affect the inflation forecast. First, changes in asset prices may affect aggregate demand directly. For example, changes in asset prices affect household wealth and consumption expenditure, affect the ability of enterprises to raise funds and thereby influence investment spending, and raise the value of collateral which affects the willingness of banks to lend. Similarly, sharp changes in exchange rates affect the demand for net exports. To the extent that there is no other information to suggest that the movement in asset prices is warranted by the underlying fundamentals of the economy, the central bank may wish to offset such changes in order to avoid unnecessary output and price variability.
Second, asset prices are strongly influenced by expectations of future returns, which in turn are related to expectations of future economic activity, inflation and monetary policy. Thus, even if their impact on aggregate demand is limited, they may contain useful information about current and future economic conditions. This information may be used to improve the inflation forecast on which the direction of monetary policy is based. The optimal policy response to asset prices for this reason will depend on the information contained in these prices. A number of authors have recently warned against the incorporation of asset prices in monetary-policy feedback rules (Fuhrer and Moore 1992; Woodford 1994). In the concluding part of Section 2.2, this criticism is briefly discussed.
Since the early 1990s, a number of central banks have incorporated the exchange rate in their inflation-targeting framework by using a monetary conditions index (MCI) – that is, a weighted average of a short-term interest rate and the exchange rate – as an operating target. The analysis in Section 2 suggests that this idea could be extended to other asset prices that affect aggregate demand. In Section 3, I therefore discuss the advantages and pitfalls of setting monetary policy in terms of an MCI. Using an MCI is beneficial in terms of practicality and because it contributes to transparency about how the central bank intends to achieve its announced inflation target. There are, however, two potentially serious limitations which in part follow from the simplicity of the MCI concept. First, the policy focus on interest rates or exchange rates may need to vary over time, for example, depending on which sectors are the cause of inflationary pressures. Second, the MCI concept ignores the potentially useful informational role of asset-price movements mentioned above.
In Section 4, I analyse the monetary-policy response to financial-asset prices and, in particular, the exchange rate in Australia and Canada. While the central banks of both countries have announced explicit inflation targets since the early 1990s, their views on how to respond to unexplained exchange-rate movements differ. In contrast to the Bank of Canada which uses an MCI, the Reserve Bank of Australia has resisted systematically responding to unexplained exchange-rate movements. In Section 4.1, I estimate a policy reaction function for both central banks over the period 1989–96 using a methodology proposed by Clarida, Galí and Gertler (1997). The estimated parameters confirm that while both central banks strongly respond to deviations of inflation from the announced target, their short-term response to the exchange rate is indeed different. I also examine whether the two central banks attach any weight to the long-term interest rate or the stock-market index in their short-run policy settings.
Finally, in Section 4.2, I examine whether, in accordance with the theoretical results of Section 2, differences in the sources of exchange-rate innovations can explain the different policy response to unexpected exchange-rate movements in the two countries. If most of the exchange-rate innovations are related to changes in the real economy, it may be optimal not to respond. In contrast, offsetting the effects of unexplained exchange-rate changes on aggregate demand is optimal, if most of the shocks to the exchange rate are financial. Using a set of structural VAR models, I find some evidence that terms-of-trade shocks are more important in Australia than in Canada, while the reverse is true for nominal shocks, in particular during the most recent period. Section 5 concludes and suggests two other reasons why asset prices may play a role in monetary-policy formulation.
2. Financial Prices and Optimal Monetary Policy
2.1 A simple model
I start the analysis of the interaction between financial prices and monetary policy by developing a stylised model of the economy. The model is an extension of that used by Gerlach and Smets (1996) to analyse the optimal policy response to the exchange rate. In this paper I focus on a general asset price and demonstrate that the same principles govern the optimal response to any asset price whether it is an exchange rate, equity prices or bond prices. Although the model is very simple, it does capture the two most important reasons why monetary authorities may want to respond to financial prices in their pursuit of price stability. First, shocks to financial prices that are not driven by fundamentals may destabilise the economy through their effects on aggregate demand, in which case the central bank may want to offset them. Second, asset prices are determined by arbitrage equations in which expectations of future returns play an important role. As a result, these prices may contain additional information about current and future economic conditions that may be useful to the monetary authorities in their stabilisation policy.
Equations (1) to (6) describe the economy:
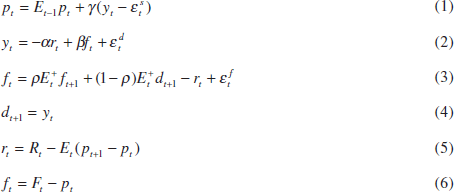
where all variables, except the interest rates, are in logarithms, and the constants have been normalised to zero.
Equation (1) is a simple Phillips curve which states that prices (pt) are determined by last period's expectations of
the current price level and the output gap 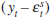 . Such a relationship
can be derived in an economy where prices are determined as a mark-up over
wages and wages are set one period in advance
(Canzoneri and Henderson 1991).
. Such a relationship
can be derived in an economy where prices are determined as a mark-up over
wages and wages are set one period in advance
(Canzoneri and Henderson 1991).
According to Equation (2), aggregate demand depends negatively on the expected real
interest rate (rt) and positively on a real asset price (ft).
Different interpretations of ft are possible. In what follows
I will mainly think of ft
as a real stock price. Equation (3) is then a log-linear approximation of the arbitrage
equation which requires the real return on equities, which can be decomposed
into the expected dividend yield and the expected capital gain, to equal the
real riskless rate plus a time-varying risk premium 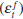 . Et xt+i
denotes the expectation of variable x at time t + i, based
on information available at time t. As discussed below, I allow for
the fact that the information set of the asset-market participants may be larger
than that of the other agents in the economy. Expectations based on this larger
information set are denoted by
. Et xt+i
denotes the expectation of variable x at time t + i, based
on information available at time t. As discussed below, I allow for
the fact that the information set of the asset-market participants may be larger
than that of the other agents in the economy. Expectations based on this larger
information set are denoted by 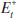 . According to Equation
(4) the expected real dividend on equities is proportional to output. Since
stocks are claims on output, note that, for β = 1, Equation (2)
then simply says that the share of demand in total wealth is a function of
the real interest rate.
. According to Equation
(4) the expected real dividend on equities is proportional to output. Since
stocks are claims on output, note that, for β = 1, Equation (2)
then simply says that the share of demand in total wealth is a function of
the real interest rate.
Gerlach and Smets (1996) interpret ft as a real exchange rate. The parameter β then captures the effect of the real exchange rate on aggregate demand, which will depend on, for example, the size of the traded-goods sector. For ρ = 1, the arbitrage Equation (3) becomes

This can then be interpreted as an uncovered interest-rate parity condition, provided the foreign interest rate and prices are normalised to be constant at zero. Finally, if dividends are constant (i.e. dt = 0), then the real asset price can also be viewed as a real bond price.
Equations (5) and (6) define the expected real interest rate as the difference between the nominal interest rate and the expected inflation rate over the period and the real asset price as the difference between the nominal asset price (Ft) and the current price level.
The central bank sets the nominal interest rate to minimise the following intertemporal loss function,
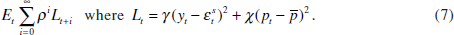
The central bank cares about both deviations of output from potential and deviations
of prices from target. Two aspects of this loss function deserve to be highlighted.
First, the central bank has no incentive to push output beyond its natural
level (given by 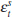 ) and, as a result, is not subject to an inflation
bias as in Barro and
Gordon (1983).
Second, the loss function implies that the central bank tries to stabilise the price
level rather than the inflation rate. This is done for convenience, as targeting
the inflation rate complicates the derivation of the optimal reaction function
under asymmetric information without affecting the main results. Moreover,
I assume that the price target is constant over time.
) and, as a result, is not subject to an inflation
bias as in Barro and
Gordon (1983).
Second, the loss function implies that the central bank tries to stabilise the price
level rather than the inflation rate. This is done for convenience, as targeting
the inflation rate complicates the derivation of the optimal reaction function
under asymmetric information without affecting the main results. Moreover,
I assume that the price target is constant over time.
Next, I discuss the assumptions regarding the information set available to the different agents in the economy. First, all agents (the central bank, wage setters and financial-market participants) know the parameters and the distribution of the disturbances of the model. Second, all agents observe last period's realisation of the price level and output, and the current nominal interest rate and asset price. This assumption can be rationalised in two ways. First, while asset prices are continually quoted in auction-like markets, the collection of data on output and prices is more cumbersome and takes some time. Alternatively, in a dynamic model which would incorporate lags in the transmission mechanism, it is future output and prices – by definition currently unobservable – rather than current output and prices that would enter the objective function.
More controversially, I allow for the possibility that asset-market participants do have some information on current output and prices. One justification is that asset-market participants have financial incentives to acquire this information as their profits depend on how good their forecast of current and future returns is. For example, stock-market analysts have an incentive to gather detailed firm-level information to forecast corporate earnings. Such an argument is often made in favour of using asset prices rather than survey measures as indicators of private-sector expectations.
Finally, in order to derive the reaction function, I need to make assumptions about
the stochastic processes driving the shocks to the economy. For simplicity,
I assume that the supply shock follows a random walk, the demand shock a first-order
autoregressive process and the financial shock a white-noise process, that
is, 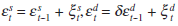 and
and
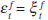 , and that the shocks are mutually uncorrelated.
, and that the shocks are mutually uncorrelated.
2.2 Optimal monetary policy
As shown in the Appendix, optimal monetary policy in this model results in setting the perceived (or forecast) price level equal to its target. However, the actual equilibrium output and price level will differ from their targets to the extent that there are unexpected excess-demand shocks which the central bank fails to stabilise. This control problem arises from a lack of information concerning the current shocks affecting the output gap and consequently the price level.[2]
In the following two subsections, I discuss the central bank's interest-rate reaction function which results in the achievement of the optimal price level.[3] In the first subsection, it is assumed that the information set of the central bank and the asset-market participants is the same. This allows me to focus on the implications of the role of the asset price in the monetary transmission mechanism for the optimal policy response to asset prices. In the second subsection, I investigate the implications of the informational role of asset prices by assuming that asset-market participants observe the current demand and supply shocks.
2.2.1 Asset prices and their role in the monetary transmission mechanism
When asset markets do not contain additional information concerning current demand and supply shocks, the optimal reaction function is given by
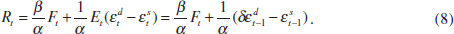
In order to achieve the optimal price level, the central bank tightens policy rates in response to a rise in the asset price and perceived excess-demand shocks to the output gap. In this case the perceived output gap is just a function of past supply and demand shocks. To understand the rationale behind this reaction function, note from Equations (1) and (2) that for given price expectations and holding the interest-rate and exchange-rate path unchanged, excess-demand shocks will directly feed through into prices. As monetary policy affects prices through the effect of interest rates and asset prices on aggregate demand, it is optimal to change interest rates in such a way that the combined effect of the interest-rate and asset-price movements offsets the effect of the shocks to the output gap.
The equilibrium asset price and interest rate are then given by
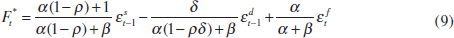
and
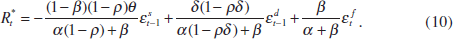
On the basis of Equations (8) to (10) two observations can be made. First, Equation (8) highlights the asset price's role in the transmission mechanism. If β = 0, i.e. the asset price does not affect aggregate demand, then it drops out of the reaction function. Moreover, by rewriting Equation (8), the optimal reaction function can be interpreted as the central bank setting a weighted average of the interest rate and the asset price – a monetary conditions index (MCI) – in response to perceived changes in the output gap:

If the asset price is the exchange rate, Equation (11) shows that the practice of setting monetary policy in terms of a weighted average of the interest rate and the exchange rate, with the weights determined by their respective effects on aggregate demand, is optimal in this particular model (Gerlach and Smets 1996). More generally, an MCI should also include other asset prices such as long-term interest rates and stock prices that affect aggregate demand.
Second, Equations (10) and (11) are equivalent policy rules. This serves to highlight two misconceptions that sometimes arise in discussions about the usefulness of MCIs. First, using an MCI as the operating target does not imply an automatic reaction to all asset-price changes, as the response depends on the perceived output gap. In fact, if β = 1, the correlation between asset-price movements and the short-term interest rate will be zero in the case of supply shocks, negative in the case of demand shocks and positive in the case of financial shocks. Second, by the same token, it is clear that using an MCI as the operating target does not obviate the need to determine the source of the asset-price shocks. Freedman (1994) emphasised that policy-makers who use an MCI as the operating target need to make a distinction between shocks that affect the desired MCI (i.e. the left-hand side of Equation (11)), such as demand and supply shocks, and shocks that do not, such as financial shocks.
2.2.2 The informational role of asset prices
In this section, I investigate the implications of the informational role of asset prices for the optimal policy response. I therefore assume that asset-market participants have information about current supply and demand shocks.[4] In this case financial prices may affect policy rates through their effect on the perceived output gap.
In the Appendix I show how to solve for the optimal response to the asset price in two steps. First, I postulate a particular form of the optimal interest-rate reaction function to the asset price and calculate the equilibrium asset price that would be consistent with such a reaction function. Given the expression of the asset price, I can then solve for the signal-extraction problem of the central bank and calculate the optimal response to the asset price. As an illustration, I analyse here the special case when there are only two fundamental shocks to the economy: a permanent supply shock and a temporary financial shock.
Consider first the case of β = 1. As can be seen from Equation (10), in this case it is optimal for the central bank not to respond to supply shocks in the symmetric information case. The reason for this is that the rise in stock prices, in response to the improved supply side of the economy, increases demand enough to close the output gap. Stock prices play an equilibrating role in response to supply shocks. In contrast, policy rates need to move strongly in response to financial shocks.
Under asymmetric information, the optimal interest-rate reaction function is
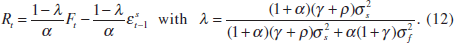
As 0 ≤ λ ≤ 1, it is clear from comparing Equations (8) and (12) that,
when stock prices contain information about the current supply shock, the optimal
policy response to them will be reduced. In determining how much lower the
response will be, the most important factor is the ratio of the variance of
supply shocks 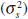 relative to the variance of financial shocks
relative to the variance of financial shocks
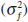 . This signal-to-noise ratio can be interpreted
as an indicator of the information content of changes in stock prices. As financial
shocks become increasingly important, this ratio tends to zero and the informational
role of the asset price is lost and the optimal policy reaction function reverts
to Equation (8). In contrast, if financial shocks to stock prices are rare,
the central bank concludes that most unexpected changes in stock prices are
due to supply shocks. Since such movements in the stock market are equilibrating
the goods market, the central bank wants to accommodate them. As λ→1,
the central bank no longer responds to changes in the stock market, which is
the optimal response in the face of supply
shocks.[5]
Thus, this example shows that the informational role of asset prices may change
the optimal response to asset prices from firm leaning against the wind to
complete laissez-faire.
. This signal-to-noise ratio can be interpreted
as an indicator of the information content of changes in stock prices. As financial
shocks become increasingly important, this ratio tends to zero and the informational
role of the asset price is lost and the optimal policy reaction function reverts
to Equation (8). In contrast, if financial shocks to stock prices are rare,
the central bank concludes that most unexpected changes in stock prices are
due to supply shocks. Since such movements in the stock market are equilibrating
the goods market, the central bank wants to accommodate them. As λ→1,
the central bank no longer responds to changes in the stock market, which is
the optimal response in the face of supply
shocks.[5]
Thus, this example shows that the informational role of asset prices may change
the optimal response to asset prices from firm leaning against the wind to
complete laissez-faire.
Take now the case in which stock prices have no effect on aggregate demand (β = 0), so that it is never optimal to respond to stock prices in the symmetric information case. When current stock prices contain information about current supply shocks, the optimal reaction function becomes
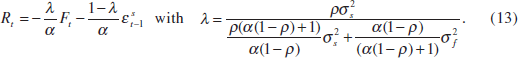
Because rising equity prices signal positive supply shocks, which in turn lower the inflation forecast, it now becomes optimal to lower policy rates in response to a booming stock market.
2.2.3 Conclusions
In this section, I have shown that the optimal monetary-policy response to changes in asset prices depends on their role in the monetary transmission mechanism and the sources of the shocks affecting them. Recently, a number of authors have criticised the use of asset prices in feedback rules of monetary policy. This criticism has basically taken two forms. The first set of arguments are a manifestation of the well-known Lucas critique. Fuhrer and Moore (1992), for example, analyse the implications of the use of simple feedback rules for monetary policy to various asset prices in an overlapping-contracts model and show that including the asset prices themselves in the reaction function can change the direction of the indicator properties. Woodford (1994) observes that econometric evaluations on whether an asset price has good forecasting power may not be relevant. On the one hand, it may not be desirable to base policy on an indicator which has been found useful in forecasting inflation, because the forecasting ability may be impaired by the very fact that the monetary authority responds to it. A specific example of this phenomenon is analysed by Estrella (1996), who shows within a simple model that the ability of the slope of the term structure to forecast economic activity and inflation may disappear under a strict inflation-targeting rule. On the other hand, low forecasting power may not justify ignoring an indicator if the absence of it simply means that the variable is already used by central banks in the conduct of policy.
The second form of criticism concerns the existence and uniqueness of equilibria when the central bank, in setting its policy rule, uses private-sector forecasts which themselves are based on expected monetary policy (Bernanke and Woodford 1996). For example, Fuhrer and Moore (1992) find that placing too much weight on asset prices in the reaction function, may lead to instability as policy loses control of inflation. Similarly, Woodford (1994) and Bernanke and Woodford (1996) show that automatic monetary-policy feedback from such indicators can create instability due to self-fulfilling expectations.
The analysis in these papers shows that automatic policy feedback from changes in financial-asset prices and private-sector inflation forecasts may be dangerous. However, the use of a structural model to interpret observed changes in asset prices reduces the two potential problems. First, the Lucas critique is not valid because the new information is evaluated within the context of the central bank's structural model and not just on the basis of forecasting ability. Second, the potential for instability or non-existence of equilibria is reduced because the response to asset prices is conditioned by the information asset prices contain concerning the structural shocks to the economy and their implications for the achievement of the central bank's inflation objective. In particular, the use of a structural model allows the central bank to filter out how much of the movement in asset prices is due to the expected monetary-policy response so that the problem of ‘circularity’ disappears (Bernanke and Woodford 1996, p. 3).
3. Advantages and Pitfalls of an MCI as an Operating Target
Recently, the Bank of Canada has formalised the role of the exchange rate in its inflation-targeting framework by using a weighted average of a short-term interest rate and the exchange rate – an MCI – as an operating target.[6] In the Canadian context, the inclusion of a short-term interest rate and an exchange rate in the MCI was motivated by research findings that inflationary pressures were largely determined by the output gap and that monetary policy affected the output gap mainly through the effects of the exchange rate and short-term interest rates on aggregate demand (Duguay 1994; Longworth and Poloz 1995). It was therefore natural to monitor a weighted average of the two, with the weights determined by their relative importance in affecting demand.
The analysis in Section 2.2 suggests that, more generally, the MCI could be extended to include other asset prices that affect aggregate demand. Indeed, in research at the European Monetary Institute a long-term interest rate was included on the grounds that these rates matter more for aggregate demand in many continental European countries (Banque de France 1996). Similarly, it could be argued that in Japan, where the effects of equity prices on economic activity are shown to be stronger than in many other countries, the MCI should include a stock-price index. In this section, I therefore discuss some of the advantages and pitfalls of setting monetary policy using an MCI. Most of the arguments that relate to an MCI which only includes the short-term interest rate and the exchange rate, also carry over to a broader MCI.
3.1 Advantages
One advantage of using an MCI as the operating target is that it is practical to formulate monetary policy in terms of the financial-asset prices that matter in the transmission process, because it is in general difficult to predict the response of asset markets to changes in policy rates (Freedman 1994). Having a target for the MCI automatically achieves the desired monetary-policy stance in the presence of uncertainty about how financial markets will respond.
A second advantage is that it clarifies the central bank's view of the monetary transmission mechanism. This increased transparency may be more important in a monetary-policy strategy which does not rely on intermediate targets to communicate policy decisions. Moreover, announcing the desired path of monetary conditions improves the transparency of the intentions of the monetary authorities and by reducing financial-market volatility may make policy more effective.[7]
3.2 Pitfalls
Two sets of problems may reduce the desirability of using an MCI as the operating target (Gerlach and Smets 1996). First, the concept of an MCI depends on a simple view of the transmission mechanism which may only be a poor approximation of the actual working of the economy. Second, its use presumes that most unexplained movements in asset prices are not related to the fundamentals of the underlying economy and therefore need to be stabilised. It therefore potentially underestimates the informational and equilibrating role of asset-price innovations. I discuss each of these arguments in turn.
The model on which the MCI concept is based may be deficient in a number of ways. First, monetary policy may affect inflation through transmission channels other than through the output gap, for instance through the direct effect of exchange rates on import prices. Until recently, the Reserve Bank of New Zealand focused on this more direct transmission channel to control inflation (Grimes and Wong 1994). While such direct price effects are important, Freedman (1994) argues that they are best interpreted as only affecting the price level and can hence be accommodated without necessarily triggering ongoing inflation. Stochastic simulations by Black, Macklem and Rose (1997) suggest that controlling inflation through the output gap rather than through import prices may lead to higher inflation variability, but appears more appealing in terms of output, interest-rate and exchange-rate volatility.
A second problem arises from the assumed constancy of the demand elasticities. The effects of interest rates and exchange rates on aggregate demand may depend on the structure of indebtedness of the economy. For example, in a country with a large foreign debt, exchange-rate changes may have important wealth effects potentially offsetting the direct effects on aggregate demand. Possibly even more important is the fact that exchange-rate movements primarily affect the tradable-goods sector, while changes in interest rates have a potentially stronger impact on non-tradable-goods sectors such as the housing market. The model underlying a fixed-weight MCI assumes that resources can be shifted relatively easily from one sector to the other so that only the economy-wide output gap matters. In practice, inflationary pressures may arise from bottlenecks in different sectors at different times. In such a situation the weight on the relevant asset price should shift (King 1997).
Finally, the lags with which the exchange rate and the interest rate affect aggregate demand may be different. Indeed, simulations with macroeconometric models suggest that exchange-rate changes have more immediate effects on real economic activity than changes in interest rates (Smets 1995). If so, changes in interest and exchange rates that leave the MCI unaffected will change aggregate demand.
The second set of problems with the concept of an MCI relates to its neglect of the potential informational and equilibrating role of asset-price innovations. As discussed in Section 2 and Gerlach and Smets (1996), the optimal weight on the exchange rate in the MCI will depend on its information content. When unexplained exchange-rate innovations are primarily driven by underlying terms-of-trade shocks, then, depending on the parameters of the model, it may actually be optimal to respond to an appreciation by raising interest rates as the exchange rate signals a rise in the demand for home goods which may lead to inflationary pressures. On the other hand, if most innovations in the exchange rate are considered to be financial and related to changes in risk premia or the credibility of monetary and fiscal policy, then the MCI weights as usually determined are optimal. The central bank's view on what drives unexpected changes in the exchange rate is thus important in deriving the optimal response and the implicit weight in an MCI. In Section 4.2 this is further explored to explain the different response to the exchange rate in Canada and Australia.[8]
This point also raises the general issue whether central banks know enough about asset-price determination to usefully target them in an MCI. Using an MCI presupposes that the central bank knows what the equilibrium asset price should be. If this is not the case, targeting a desired path for the MCI may hinder the equilibrating role of asset prices. For example, in the simple example of Section 2.2 with β = 1 and asymmetric information, if the central bank acts according to Equation (8), then the equilibrating role of the response of equity prices to supply shocks would be undone by the monetary-policy response and output and price variability would be larger than under laissez-faire.
In practice, there appears to be a trade-off between avoiding letting financial shocks destabilise the economy and the possibility that a policy response hinders the equilibrating role of asset prices. When there is genuine uncertainty concerning what drives financial prices, the potential for asset-price misalignments to destabilise the economy will be a determining factor. Thus, if the demand effects of changes in a particular asset price are limited, the central bank's bias will be not to interfere with the market. On the other hand, if unwarranted movements in the asset price can have strong and lasting effects on output and prices, a policy of leaning against such changes may be cautious.
4. Financial-asset Prices and Monetary Policy in Australia and Canada
4.1 Estimating a policy reaction function
Since the early 1990s both the Bank of Canada and the Reserve Bank of Australia have had publicly announced explicit targets for inflation. The Bank of Canada announced inflation-reduction bands in February 1991 and has, since 1995, been targeting the inflation rate within a band of ±1 per cent around a midpoint target of 2 per cent. The Reserve Bank of Australia started publicly quantifying its inflation objective in 1993, announcing a target of 2–3 per cent on average over the course of the business cycle. However, while the Bank of Canada has incorporated the exchange rate in the inflation-targeting framework by using an MCI as the operating target, the Reserve Bank of Australia has resisted systematically responding to unexpected exchange-rate movements.[9]
In this Section I attempt to quantify the commitment to low inflation and test the
different attitude towards the exchange rate by estimating a policy reaction
function for the Bank of Canada and Reserve Bank of Australia over the
period 1989–96, using the methodology proposed by Clarida, Galí
and Gertler
(1997).[10]
They assume that within each operating period the central bank has a target
for the nominal policy-controlled interest rate,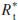 , which is based on
the state of the economy. In particular, the target depends on perceived inflation
and output,
, which is based on
the state of the economy. In particular, the target depends on perceived inflation
and output,
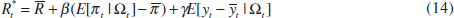
where 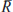 is the equilibrium nominal interest rate,
πt the trend inflation rate,
is the equilibrium nominal interest rate,
πt the trend inflation rate, 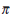 the inflation target
and
the inflation target
and 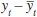 the current output gap.
the current output gap.
This target rule is a generalisation of the type of simple interest-rate rules proposed by Taylor (1993).[11] It can be derived as the optimal rule for a central bank that has a quadratic loss function over inflation and output in a model similar to that in Section 2 (Svensson 1997). For this target rule to lead to an effective stabilisation of the inflation rate, β needs to be greater than one and γ positive, so that the real policy rate rises whenever trend inflation is above target and/or output is above potential.
In order to derive the equation estimated in Table 1, three more steps are necessary. First, as discussed extensively in Lowe and Ellis at this conference, central banks tend to smooth changes in interest rates. This interest-rate smoothing is captured by assuming that the actual rate partially adjusts to the target as follows:
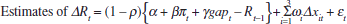 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|
| Country | β | γ | ρ | ω1 | ω2 | ω3 | α | 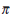 |
 |
| Model 1 | |||||||||
| Australia | 2.83 (0.37) |
0.35 (0.31) |
0.60 (0.11) |
— — |
— — |
— — |
−0.00 (0.00) |
2.2 | 4.5 |
| Canada | 2.23 (0.69) |
1.05 (0.72) |
0.77 (0.07) |
— — |
— — |
— — |
0.01 (0.01) |
1.5 | 4.1 |
| Model 2 | |||||||||
| Australia | 2.84 (0.36) |
0.33 (0.30) |
0.60 (0.11) |
0.00 (0.01) |
— — |
— — |
−0.00 (0.00) |
2.2 | 4.5 |
| Canada | 2.91 (0.67) |
2.01 (0.90) |
0.85 (0.05) |
−0.22 (0.05) |
— — |
— — |
−0.01 (0.02) |
2.5 | 2.4 |
| Model 3 | |||||||||
| Australia | 2.83 (0.37) |
0.36 (0.26) |
0.61 (0.10) |
0.00 (0.02) |
0.02 (0.15) |
0.00 (0.01) |
−0.00 (0.00) |
2.2 | 4.5 |
| Canada | 2.45 (0.52) |
1.14 (0.32) |
0.77 (0.04) |
−0.14 (0.05) |
−0.09 (0.11) |
−0.06 (0.02) |
0.01 (0.01) |
1.6 | 4.0 |
| Model 4 | |||||||||
| Australia | 3.09 (0.25) |
— — |
0.54 (0.09) |
— — |
— — |
— — |
−0.00 (0.00) |
2.3 | 4.4 |
| Canada | 2.50 (0.55) |
1.19 (0.34) |
0.79 (0.03) |
−0.14 (0.05) |
— — |
−0.06 (0.02) |
0.00 (0.01) |
1.7 | 3.9 |
| Model 5 | |||||||||
| Australia | 2.84 (0.33) |
0.26 (0.13) |
0.60 (0.10) |
— — |
— — |
— — |
0.00 (0.00) |
2.0 | 3.9 |
| Canada | 0.85 (0.27) |
1.00 (0.11) |
0.61 (0.04) |
−0.15 (0.04) |
— — |
−0.06 (0.01) |
0.06 (0.00) |
2.2 | 6.4 |
| Notes: Estimates are obtained by GMM with correction for MA(3) autocorrelation. The optimal-weighting matrix is obtained from the first-step two-stage non-linear least squares parameter estimates. The sample period is 1989:Q1–1996:Q3. In models 1 to 4, Rt is the day-to-day interest rate, πt is the centred annual underlying inflation rate, gapt is the output gap using a HP(1600) filter to generate the potential-output series. The three asset prices are a nominal trade-weighted exchange rate, a 10-year nominal government bond yield and a broad stock-market index. The instruments used are mentioned in the text. Standard errors are shown in parentheses. | |||||||||

where the parameter ρ captures the degree of interest-rate smoothing and vt
reflects a white-noise control error. Letting 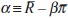 and
and 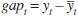 , and combining Equations
(14) and (15), the policy reaction becomes
, and combining Equations
(14) and (15), the policy reaction becomes
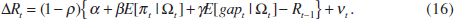
Second, in analogy with Equations (8) and (12) of the model in Section 2, I allow the policy rate to respond to contemporaneous changes in asset prices. Financial prices may affect current policy rates either because they have an independent impact on future inflation or because they contain information about current trend inflation and the output gap not captured in the instrument set.[12] Adding asset prices to the reaction function yields
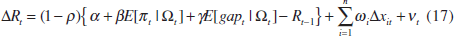
where ωi is the response to the change in the ith financial variable. In Table 1, I consider three such variables: a nominal trade-weighted exchange rate, a 10-year nominal bond yield and a broad stock-market index.
Finally, I eliminate the unobserved variables by rewriting the policy rule in terms of realised variables as follows:
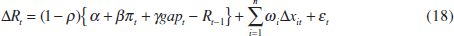
where the error term 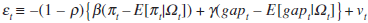 .
.
Table 1 reports GMM estimates of Equation (18) using quarterly data over the period 1989:Q1–1996:Q3.[13] The instruments used are two lags of quarterly changes in the underlying inflation rate, the log terms of trade, the policy rate and the three financial variables, two lags in the output gap and the contemporaneous US interest rate, the US/DM exchange rate, the 10-year bond yield and the S&P500 index. In the benchmark model the output gap is calculated as the deviation of actual real GDP from a Hodrick-Prescott (λ = 1600) generated potential output series (models 1 to 4 of Table 1). In model 5 of Table 1, a quarterly interpolation of the OECD's estimate of the output gap is used.
While the empirical model does not separately identify the inflation target 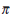 and the equilibrium real rate
and the equilibrium real rate 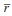 , it does provide
a relation between the two variables that is conditional upon α
and β, which is given by
, it does provide
a relation between the two variables that is conditional upon α
and β, which is given by 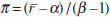 . The second-to-last
column of Table 1 gives the implied estimate of the inflation target, using
the average real short-term rate over the period 1973–96 as an estimate
of the equilibrium real rate. The average real rate over this period is 3.49
per cent in Canada and
4.04 per cent in Australia. The last column reports the implied estimate
of the equilibrium real rate using the midpoint of the announced target band
as an estimate of the inflation target
(2 per cent in Canada and
2.5 per cent in Australia).
. The second-to-last
column of Table 1 gives the implied estimate of the inflation target, using
the average real short-term rate over the period 1973–96 as an estimate
of the equilibrium real rate. The average real rate over this period is 3.49
per cent in Canada and
4.04 per cent in Australia. The last column reports the implied estimate
of the equilibrium real rate using the midpoint of the announced target band
as an estimate of the inflation target
(2 per cent in Canada and
2.5 per cent in Australia).
In spite of the short sample, the results are quite promising. Model 4 in Table 1 shows the results of the preferred specification. In both countries the parameter on trend inflation is significantly larger than one, indicating the commitment to stable inflation during this period. Moreover, using the average real short rate over the period 1973–96 as an estimate of the equilibrium real rate, the estimated inflation target is close to and not significantly different from the midpoint of the announced inflation bands (2.3 per cent in Australia and 1.7 per cent in Canada). The estimated response to the output gap is strong and significant in Canada: policy rates are increased by more than 1 percentage point for every 1 percentage point increase of the output gap. In Australia, the response is positive (about 0.33) but insignificant (see model 2).
The estimated responses to changes in the three financial variables (model 3), show that, as expected, the Bank of Canada reduces policy rates significantly in response to an appreciation of the trade-weighted exchange rate. The implied estimated weight on the exchange rate (0.12) is about half the size of the announced weight of one-fourth. More surprisingly, changes in the stock-market index are also significant in the policy reaction function of the Bank of Canada. Moreover, the sign of the estimated elasticity suggests that policy rates were eased during the estimation period in response to a rise in the stock market. In light of the theoretical model of Section 2, this can be rationalised if a rise in the stock market reflects positive supply developments which expand output and reduce inflation. An alternative and maybe more plausible explanation is that both the central bank and the stock market respond to news about underlying inflation that is not captured by the instrument set. In contrast, the Reserve Bank of Australia does not respond to changes in any of the asset prices including the exchange rate.
The last model of Table 1 shows the effect of using the OECD's estimate of the output gap in the estimation of Equation (18). In the Australian case, the parameter estimates hardly change, but the policy response to the output gap is now significant. The estimate of the parameter γ implies that the Australian cash rate is raised by around 25 basis points for every 1 per cent rise in output above the OECD's estimate of potential. The Canadian results are less robust to the alternative specification of the output gap: the parameter on trend inflation drops to 0.85, not significantly different from 1, while the parameter on the output gap remains strong and is quite precisely estimated. A 1 percentage point rise in output above potential leads to a tightening of the interest rate by 1 percentage point.
4.2 Sources of exchange-rate variation and the policy response
Section 2 demonstrated that the source of unexplained exchange-rate movements and its implications for future inflation determine the optimal reaction coefficient to contemporaneous exchange-rate shocks. If exchange-rate innovations mainly signal relative shifts in the demand and supply of domestically produced goods, then the central bank may want to accommodate or even reinforce such exchange-rate movements. On the other hand, if most exchange-rate innovations are financial, the central bank may wish to lean against them. In this Section I try to identify the sources of exchange-rate innovations in Australia and Canada and analyse whether these can explain the different attitude towards the exchange rate.
To investigate the sources of exchange-rate movements in both countries, I use a set of VAR models, each of which incorporates at a minimum both the nominal bilateral exchange rate against the US dollar and the relative GDP deflator vis-à-vis the United States.[14] The structural shocks are identified using triangular long-run zero restrictions (Blanchard and Quah 1989). Long-run restrictions are favoured over short-run restrictions for two reasons. First, because I am interested in uncovering the source of the shocks of the contemporaneous innovations in the nominal exchange rate, it is more appealing not to impose any identification restrictions on the contemporaneous correlations. Second, my primary interest is to distinguish between real and nominal shocks for which the long-run restrictions are particularly suited.
Each model is estimated over two subperiods. The first subperiod, which starts after the breakdown of the Bretton Woods system and ends in the last quarter of 1989, has the advantage of excluding the most recent period which was characterised by a shift in monetary-policy regime which may have affected the source of exchange-rate shocks. The second subperiod, which starts in 1980 and ends in 1996, excludes the potentially large effects of the two oil price shocks.[15]
For each of the models, Table 2 reports the percentage of contemporaneous and four-quarter-ahead forecast errors in the nominal exchange rate and of four- and eight-quarter-ahead forecast errors in relative prices that can be explained by the various shocks. This allows me to discuss the relative importance of the different sources of shocks to current exchange-rate innovations and their contribution to the variability in relative prices one to two years ahead.
| 1973:Q1–1989:Q4 | 1980:Q1–1996:Q4 | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Australia | Canada | Australia | Canada | ||||||||||||||||
| Exchange rate | Relative prices | Exchange rate | Relative prices | Exchange rate | Relative prices | Exchange rate | Relative prices | ||||||||||||
| Model 1: Real exchange rate, relative prices | |||||||||||||||||||
| Real | 99 | (98) | 0 | (2) | 99 | (94) | 13 | (17) | 91 | (83) | 8 | (7) | 58 | (82) | 59 | (62) | |||
| Nominal | 0 | (2) | 99 | (97) | 0 | (5) | 86 | (82) | 8 | (16) | 91 | (92) | 41 | (17) | 40 | (37) | |||
| Model 2: Relative output, real exchange rate, relative prices | |||||||||||||||||||
| Supply | 39 | (37) | 8 | (3) | 10 | (6) | 8 | (9) | 22 | (31) | 11 | (13) | 1 | (1) | 8 | (2) | |||
| Demand | 60 | (60) | 3 | (3) | 87 | (85) | 1 | (6) | 62 | (50) | 26 | (26) | 67 | (86) | 37 | (45) | |||
| Nominal | 0 | (1) | 88 | (92) | 2 | (8) | 89 | (83) | 15 | (17) | 61 | (60) | 30 | (12) | 53 | (51) | |||
| Model 3: Terms of trade, real exchange rate, relative prices | |||||||||||||||||||
| Terms of trade | 65 | (70) | 1 | (3) | 20 | (17) | 10 | (9) | 65 | (62) | 13 | (11) | 32 | (43) | 11 | (8) | |||
| Real | 33 | (26) | 1 | (1) | 78 | (80) | 11 | (15) | 24 | (15) | 0 | (0) | 33 | (44) | 45 | (54) | |||
| Nominal | 0 | (3) | 96 | (94) | 0 | (2) | 77 | (75) | 10 | (22) | 86 | (88) | 34 | (12) | 43 | (37) | |||
| Notes: Each of the rows shows the percentage of the forecast-error variance explained by a particular shock. The forecast horizon is 0 (4) quarter(s) for the nominal US dollar exchange rate, and 4 (8) quarters for the relative GDP deflator vis-à-vis the United States. Each of the VAR models is estimated with six lags of the endogenous variables and the shocks are identified by a long-run triangular Choleski identification scheme. | |||||||||||||||||||
Model 1 of Table 2 is a bivariate VAR model which only includes the real exchange rate and relative prices.[16] Several authors including Lastrapes (1992) and Enders and Lee (1997) have used this model to decompose the real exchange rate into real and nominal factors. The identifying assumption is that nominal shocks have no permanent effect on the real exchange rate.[17] As can be seen from Table 2, in the period before 1989, real shocks explain 99 per cent of the contemporaneous innovations in the nominal exchange rate, but contribute very little to relative price movements. In contrast, nominal shocks that explain most of the movements in relative prices are not reflected in the nominal exchange rate. For Australia, these results appear quite robust over the whole sample period, suggesting that nominal exchange-rate innovations do not contain much information concerning future inflation. In Canada, however, a remarkable shift can be detected in the second subsample: nominal shocks now explain more than 40 per cent of the contemporaneous exchange-rate innovations.
One reason why real shocks are estimated to have only limited effects on relative prices may be that in fact they are a mixture of real supply and real demand shocks. As these shocks have opposite effects on relative prices, the limited price response of the combined shock may be the result of this misspecification. Clarida and Galí (1994) distinguish between supply and demand shocks by adding relative output to the VAR system. The supply shock is then identified by the assumption that only this shock can have an impact on relative output in the long run.[18] Model 2 of Table 2 reports the results from this decomposition for Australia and Canada. The dichotomy between relative prices and exchange rates remains in the earlier period. However, supply shocks are relatively more important than demand shocks in explaining exchange-rate innovations in the Australian dollar. Reviewing the results for the second subsample, it is again clear that nominal shocks are a more important source of exchange-rate innovations in Canada. However, in this period real demand shocks also contribute to the variation in relative prices in Australia.
Following Fisher (1996), I include the terms of trade instead of relative output in model 3 of Table 2. Since both countries are net exporters of resource-based commodities and net importers of manufactures, it is not surprising that variations in the terms of trade have historically been an important determinant of the real exchange rate in both countries.[19] The identification scheme is the same as in model 2. Since both Australia and Canada are relatively small economies, the assumption that domestic real and nominal shocks cannot affect the terms of trade in the long run is probably reasonable. The results show that terms-of-trade shocks are a much more important driving force behind current exchange-rate innovations in Australia (65 per cent) than in Canada (20 per cent) (Figure 2).[20] The fact that such persistent terms-of-trade movements have only negligible effects on relative prices, may be viewed as evidence that the large exchange-rate response is effective in preventing these shocks from spilling over in domestic inflation.
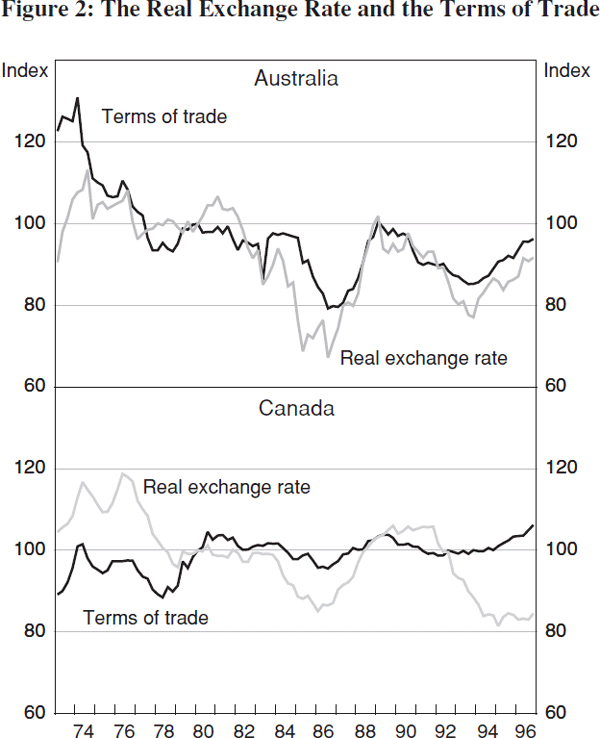
Overall, the results in Table 2 show that terms-of-trade and supply shocks contribute more to exchange-rate innovations in Australia, while in the most recent period nominal shocks contribute more in Canada. Together with more direct evidence that risk-premium shocks due to fiscal sustainability and political problems have been important in Canada during the 1990s (Clinton and Zelmer 1997), this evidence suggests that the source of the exchange-rate shocks can in part explain the different attitude towards the exchange rate of the Reserve Bank of Australia and the Bank of Canada.
5. Conclusions
This paper consists of three sections. First, using a simple model and within the context of the central bank's objective of price stability, I discuss the optimal response of monetary policy to unexpected changes in financial-asset prices. The main conclusion of this analysis is that the optimal response depends on how the asset-price movement affects the central bank's inflation forecast, which in turn depends on two factors: the role of the asset price in the transmission mechanism and the typical information content of innovations in the asset price.
Second, I analysed the advantages and disadvantages of setting monetary policy in terms of an MCI. While using an MCI as the operating target may be useful in terms of practicality and transparency when asset-price innovations are primarily driven by financial shocks, I have highlighted two potentially serious limitations which in part follow from the simplicity of the MCI concept: first, the optimal weights are likely to vary over time, not least because interest rates and exchange rates affect the traded and non-traded goods sector differently; second, the MCI concept ignores the potentially useful informational and equilibrating role of asset-price innovations.
Third, I have estimated a policy reaction function for the Reserve Bank of Australia and the Bank of Canada and found that while both central banks strongly respond to deviations of inflation from their announced target, their short-term response to the exchange rate differs. While the Bank of Canada, consistent with the idea of an MCI, systematically raises interest rates in response to a depreciation of the exchange rate, the Reserve Bank of Australia does not respond. My analysis of the sources of exchange-rate innovations in the two countries suggests that in part this can be explained by the greater importance of terms-of-trade shocks in Australia and, during the more recent period, of nominal shocks in Canada.
In this paper I have focused on the role of asset prices in the central bank's pursuit of price stability. There are at least two other reasons why asset prices may play a role in monetary-policy formulation. First, the information in asset prices may be useful in the tactics of monetary policy. As much of the implementation of monetary policy is about communication and signalling, information from the financial markets about the expected direction of policy may be useful to both assess the appropriateness of a particular timing of policy actions and its effectiveness. Second, it is sometimes suggested that, to the extent that large and persistent asset-price misalignments may give rise to widespread financial instability, asset-price stability by itself should be an important objective of the central bank (Goodhart 1995). Indeed, the experience of the late 1980s, when many countries saw a sharp increase in the prices of real and financial assets which later proved to be unsustainable and led to large-scale losses in the banking sector, shows that the misallocation costs due to such misalignments can be large. Both of these issues deserve further attention in future research.
Appendix: Optimal Monetary Policy in the Model of Section 2.1
Since the central bank does not observe current prices, I follow Canzoneri et al. (1983) and Barro and Broadbent (1995) and assume that the central bank optimises the objective function by picking the perceived price level. To implement this approach, I first derive the contemporaneous price perception errors, and then rewrite the objective function (7) in terms of the perceived price level and the price perception errors.
Combining Equations (1) and (2) and rearranging, I express the price level as a function of expectational variables, current observable variables and the excess-demand shock,
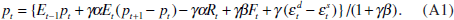
Agents who use the current interest rate and asset price in making their current
price predictions need estimate only the excess-demand disturbance, 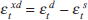 , as they either know or can calculate all
other terms on the right-hand side of Equation (8). Their current price prediction
is therefore
, as they either know or can calculate all
other terms on the right-hand side of Equation (8). Their current price prediction
is therefore
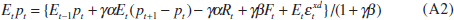
and, combining Equations (A1) and (A2), their price perception error is
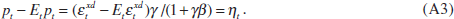
Note that if agents observed current prices, they would be able to deduce from Equation (A1) the current excess-demand shock, in which case the price perception error would be zero. If central banks do not observe current output and prices, they can still potentially extract information about the current excess-demand shock from the observed asset prices. Indeed, Equation (3) can be rewritten in nominal terms as
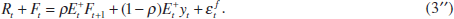
As the central bank does observe the left-hand side of Equation (3″), it observes a noisy measure of the asset-market participants' relevant expectations which may include information about current output and prices. Below I discuss how that information can be used to minimise the variance of ηt.
Optimal monetary policy
Equation (A3) can be used to rewrite the loss function in terms of the perceived current price level and a perception error,
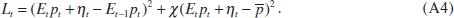
Differentiating this expression with respect to Et pt yields,[21]

Imposing the rational-expectations condition, the equilibrium solution for the perceived price level is[22]

The central bank's optimal policy is to equate the perceived price level to its target. The associated equilibrium price and output level is then[23]

and

The equilibrium output and price level differ from their targets to the extent that there are unexpected excess-demand shocks which the central bank cannot stabilise.
The next question is how the central bank should set the interest rate to achieve the optimal price level. Combining Equations (1) and (2), taking the central bank's expectations and substituting for the equilibrium price level, the optimal reaction function in terms of the nominal interest rate is given by[24]

Policy interest rates will tighten in response to a perceived output gap and a rise in the asset price. Note that the size of the response to changes in the asset price depends on its impact on aggregate demand. If β = 0, i.e. the asset price does not play any role in the transmission mechanism, then policy will not respond to movements in the asset price. However, Equation (A9) tells only part of the story. Since the asset price may contain information about the current output gap, it may affect policy rates through its effect on perceived excess demand. Before turning to this case, I first solve for the equilibrium levels of the interest rate and asset price under symmetric information.
Interest rates and asset prices under symmetric information
Next I derive the equilibrium level of the interest rate and the asset price when the financial market has no additional information on current output and prices. Equation (A9) becomes
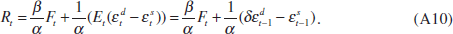
Moreover, using Equations (3), (4), (5) and (A7) and (A8) yields

Combining Equations (A10) and (A11) yields a first-order difference equation in the nominal asset price,
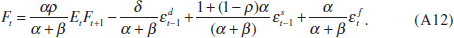
Solving Equation (A12) forward yields the equilibrium solution given in Equations (9) and (10)
Asymmetric information and the policy response to asset prices
Now I assume that the financial-market participants do have information about current output and prices, i.e. they observe the underlying supply and demand shocks. In this case the optimal response of policy rates is still governed by Equation (A9). However, this time there is a possibility that the asset price contains information about the current excess-demand shock. I solve the optimal response to the asset price in two steps. First, I postulate a particular form of the optimal interest-rate reaction function to the asset price and calculate the equilibrium asset price that would be consistent with such a reaction function. Given the expression of the asset price, I can then solve for the signal-extraction problem of the central bank and calculate the optimal response to the asset price.
In this case I can rewrite the optimal reaction function
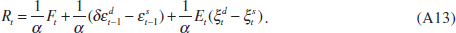
The central bank estimates the current excess-demand shock using its knowledge of the current asset price. I postulate that the signal-extraction function is of the form
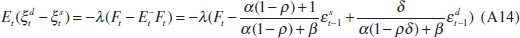
where λ is the response parameter that needs to be determined and
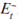 is the expectations operator based on the
information set which excludes the current asset price.
is the expectations operator based on the
information set which excludes the current asset price.
Going through the same procedure as before, the solution to a more complicated first-order forward-looking difference equation in Ft becomes
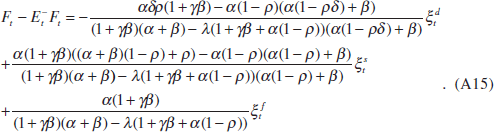
Given this solution for the unexpected change in the asset price, I can now solve the signal-extraction problem as follows,

This yields the following solution for λ,
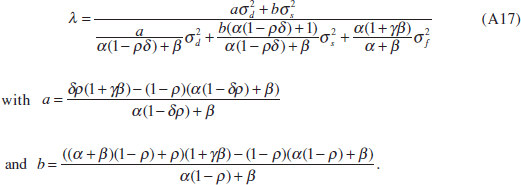
| Phillips-Perron unit root tests | Standard deviation | Correlation | ||||
|---|---|---|---|---|---|---|
| Australia | Canada | Australia | Canada | |||
| Nominal US$ exchange rate |
−1.43 | −1.37 | 3.9 | 1.6 | 0.31 | |
| Relative GDP deflator | −1.41 | −2.27 | 1.0 | 0.6 | 0.35 | |
| Terms of trade | −2.45 | −2.73 | 2.4 | 1.5 | 0.33 | |
| Johansen cointegration test | ||||||
| LR test | Cointegrating equation (CE) | |||||
| No CE | At most one CE | Nominal exchange rate | Relative prices | Terms of trade | ||
| Australia | 50** | 11 | 1 | −1.03 (0.13) | 1.86 (0.26) | |
| Canada | 23 | 10 | — | — | — | |
| Notes: *(**) denotes rejection at 5(1) per cent significance level. All variables are in logs. | ||||||
Footnotes
I thank Palle Andersen, Stefan Gerlach and Kostas Tsatsaronis for helpful comments and Gert Schnabel for statistical support. The views expressed in this paper are solely my own and not necessarily those of the BIS. [*]
The central role of the inflation forecast in inflation-targeting countries has been emphasised by Svensson (1997). [1]
These results are very similar to the results in Svensson (1996) who studies a (more realistic) dynamic model in which there is a one-period lag in both the Phillips curve and the aggregate-demand function. In that model actual output and inflation will deviate from their target levels because of shocks that occur during the control lag. [2]
The optimal reaction function is derived in the Appendix. In deriving Equations (8) to (15) a zero price target is assumed. [3]
I assume asset-market participants observe the current supply and demand shocks. This assumption is made for convenience. Alternatively, one could assume that they only observe a noisy signal of these shocks. [4]
The basic insight is, of course, not new. For example, Boyer (1978) extends the classical Poole (1970) analysis to the question of optimal foreign-exchange market intervention. [5]
See Freedman (1994). Following the Bank of Canada, central banks in a number of countries – among them Sweden, Finland, Iceland and Norway – have adopted MCIs. In contrast to Canada, however, the Nordic countries use the MCI primarily as an ex post indicator of the stance of policy. Since October 1996, the Reserve Bank of New Zealand also uses an MCI as the operating target. While the Bank of Canada only indicates the direction of its desired path, the Reserve Bank of New Zealand quantifies its desired path for both components. [6]
Similar arguments are used in favour of other instrument rules that quantify the link between the central bank's policy instrument and economic conditions; see Taylor (1996). [7]
For example, the view consistent with the analysis in Astley and Garrat (1996), that most exchange-rate innovations are driven by real shocks, may partly explain why the Bank of England has rejected the usefulness of an MCI; see also King (1997). [8]
Opinions about the usefulness of an MCI as an operating target also differ among other inflation-targeting countries. While the Reserve Bank of New Zealand started using an MCI as the operating target at the end of 1996, the Bank of England firmly rejects it (King 1997). [9]
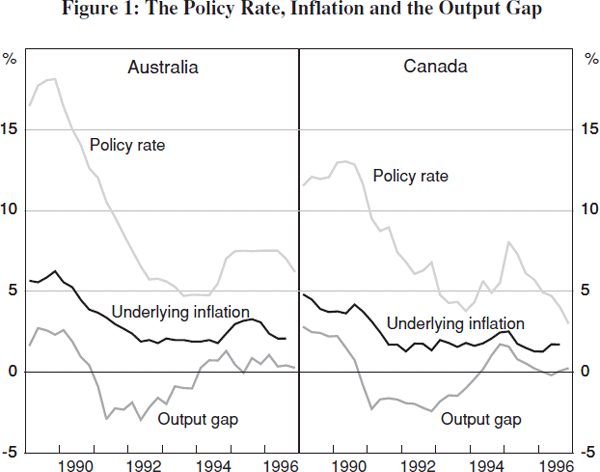
Although the announcement of the inflation targets occurred in the early 1990s, in both countries the commitment to low and stable inflation became gradually clear in the late 1980s when interest rates rose strongly to undo the upward trend in inflation (Figure 1). In Canada, the appointment of John Crow to Governor of the Bank of Canada in February 1987 marked a shift towards more emphasis on the goal of price stability. This shift was more gradual and less transparent in Australia (Debelle 1996). [10]
In contrast to Taylor (1993), Clarida, Gali and Gertler (1997) use expected inflation instead of actual inflation arguing that this makes it easier to disentangle the link between the estimated coefficients and the central bank's objectives. For example, it is not clear from the simple Taylor specification whether the central bank responds to the output gap independently of concerns about future inflation. In this paper, I use a centred annual inflation rate to capture the current trend inflation rate in Equation (14). The two reasons for doing so are that using realised future inflation, first, reduces the already short sample period, and, second, leads to biased estimates because the current interest rate affects future inflation. [11]
Clarida, Gali and Gertler (1997) interpret the significance of variables other than expected inflation in the policy reaction function as evidence in favour of other objectives than price stability (e.g. exchange-rate stability). [12]
Because the trend inflation rate is captured by a centred annual inflation rate, the composite error term has an MA(3) representation with quarterly data. In this case the GMM estimator of the parameter vector is a two-step non-linear two-stage least squares estimator when the model is overidentified. See Hansen (1982) and Cumby, Huizinga and Obstfeld (1983). [13]
All variables are included as log changes. See Table A1 for the relevant unit-root tests. [14]
Because of the limited degrees of freedom, I could not split the total sample period in two. [15]
From these two variables the impact on the nominal exchange rate reported in Table 2 can be derived. [16]
An alternative, more neutral, view is to interpret the shocks as permanent and temporary innovations to the real exchange rate. [17]
See Astley and Garrat (1996) and Chadha and Prasad (1996) for two applications of this methodology to the United Kingdom and Japan. [18]
See, for example, Gruen and Wilkinson (1994) and Fisher (1996) for Australia, and Amano and van Norden (1995) for Canada. [19]
The greater relevance of the terms of trade for the exchange rate in Australia is also confirmed by the cointegration analysis reported in Table A1. While I find a quite robust cointegrating relationship between the nominal exchange rate, relative prices and the terms of trade in Australia, it is much harder to find evidence to that effect in Canada. Amano and van Norden (1996) do find cointegration between the real exchange rate and terms of trade if they split the terms of trade into two components, one capturing energy-related sectors and the other capturing commodities versus manufactures. I was, however, not able to confirm their results using the quarterly data on the terms-of-trade variables at my disposal. [20]
The underlying assumption is that the price perception errors are independent of monetary-policy behaviour. [21]
Note that here the assumption that wage setters also do not observe current output and prices is important. [22]
In general, this need not be the case. For example, if the central bank targets the inflation rate, the price forecast error will also depend on the past price perception error. [23]
From here we assume that the price-level target is zero. Note that since current prices are not observed, neither the real interest rate nor the real stock price are known. In this case the perceived real interest rate and asset price equal the observed nominal interest rate and asset prices because the perceived price level and expected inflation are zero. [24]
References
Amano, R. and S. van Norden (1995), ‘Terms of Trade and Real Exchange Rates: The Canadian Evidence’, Journal of International Money and Finance, 14(1), pp. 83–104.
Astley, M.S. and A. Garrat (1996), ‘Interpreting Sterling Exchange Rate Movements’, Bank of England Quarterly Bulletin, 36(4), pp. 394–404.
Banque de France (1996), ‘Les Indicateurs des Conditions Monetaires’, Bulletin de la Banque de France, 30, June, pp. 1–15.
Barro, R.J. and D.B. Gordon (1983), ‘Rules, Discretion and Reputation in a Model of Monetary Policy’, Journal of Monetary Economics, 12, pp. 101–120.
Bernanke, B. and M. Woodford (1996), ‘Inflation Forecasts and Monetary Policy’, mimeo.
Black, R., T. Macklem and D. Rose (1997), On Policy Rules for Price Stability, paper presented at the Bank of Canada Conference, ‘Price Stability, Inflation Targets and Monetary Policy’, Ottawa, 3–5 May.
Blanchard, O. and D. Quah (1989), ‘The Dynamic Effects of Aggregate Demand and Supply Disturbances’, American Economic Review, 79(4), pp. 655–673.
Boyer, R.S. (1978), ‘Optimal Foreign Exchange Market Intervention’, Journal of Political Economy, 86(8), pp. 1045–1055.
Broadbent, B. and R.J. Barro (1997), ‘Central Bank Preferences and Macroeconomic Equilibrium’, Journal of Monetary Economics, 39(1), pp. 17–43.
Canzoneri, M. and D.W. Henderson (1991), Monetary Policy in Interdependent Economies, MIT Press, Cambridge, Massachusetts.
Canzoneri, M., D.W. Henderson and K.S. Rogoff (1983), ‘The Information Content of the Interest Rate and Optimal Monetary Policy’, Quarterly Journal of Economics, 98(4), pp. 545–566.
Chadha, B. and E. Prasad (1996), ‘Real Exchange Rate Fluctuations and the Business Cycle: Evidence from Japan’, IMF Working Paper No. 96/132.
Clarida, R. and J. Galí (1994), ‘Sources of Real Exchange Rate Fluctuations: How Important are Nominal Shocks?’, Carnegie-Rochester Conference Series on Public Policy, 41, pp. 1–56.
Clarida, R., J. Galí and M. Gertler (1997), ‘Monetary Policy Rules in Practice: Some International Evidence’, mimeo.
Clinton, K. and M. Zelmer (1997), ‘Aspects of Canadian Monetary Policy Conduct in the 1990s: Dealing with Uncertainty’, in BIS, Implementation and Tactics of Monetary Policy, Conference Papers Vol. 3, pp. 169–199.
Cumby, R.E., J. Huizinga and M. Obstfeld (1983), ‘Two-Step Two-Stage Least Squares Estimation in Models with Rational Expectations’, Journal of Econometrics, 21(3), pp. 333–355.
Debelle, G. (1996), ‘The Ends of Three Small Inflations: Australia, New Zealand and Canada’, Canadian Public Policy, 22(1), pp. 56–78.
Duguay, P. (1994), ‘Empirical Evidence on the Strength of the Monetary Transmission Mechanism in Canada – an Aggregate Approach’, Journal of Monetary Economics, 33(1), pp. 39–61.
Enders, W. and B.S. Lee (1997), ‘Accounting for Real and Nominal Exchange Rate Movements in the Post-Bretton Woods Period’, Journal of International Money and Finance, 16(2), pp. 233–254.
Estrella, A. (1996), ‘Why do Interest Rates Predict Macro Outcomes? A Unified Theory of Inflation, Output, Interest and Policy’, Federal Reserve Bank of New York Research Paper No. 9717.
Fisher, L.A. (1996), ‘Sources of Exchange Rate and Price Level Fluctuations in Two Commodity Exporting Countries: Australia and New Zealand’, Economic Record, 72(219), pp. 345–358.
Freedman, C. (1994), ‘The Use of Indicators and the Monetary Conditions Index in Canada’, in T.J.T. Balino and C. Cottarelli (eds), Frameworks for Monetary Stability – Policy Issues and Country Experiences, IMF, Washington D.C., pp. 458–476.
Fuhrer, J. and G. Moore (1992), ‘Monetary Policy Rules and the Indicator Properties of Asset Prices’, Journal of Monetary Economics, 29(2), pp. 303–336.
Gerlach, S. and F. Smets (1996), ‘MCIs and Monetary Policy in Open Economies under Floating Rates’, mimeo.
Goodhart, C. (1995), ‘Price Stability and Financial Fragility’, in K. Sawamoto, Z. Nakajima and H. Taguchi (eds), Financial Stability in a Changing Environment, Macmillan, Basingtoke.
Grimes, A. and J. Wong (1994), ‘The Role of the Exchange Rate in New Zealand Monetary Policy’, in R. Glick and M. Hutchinson (eds), Exchange Rate Policy and Interdependence: Perspectives from the Pacific Basin, Cambridge University Press, New York.
Gruen, D.W.R. and J. Wilkinson, (1994), ‘Australia's Real Exchange Rate: Is it Explained by the Terms of Trade or by Real Interest Differentials?’, Economic Record, 70(209), pp. 204–219.
Hansen, L. (1982), ‘Large Sample Properties of Generalised Method of Moments Estimators’, Econometrica, 50(4), pp. 1029–1054.
King, M. (1997), ‘Monetary Policy and the Exchange Rate’, Bank of England Quarterly Bulletin, 37(2), pp. 225–227.
Lastrapes, W.D. (1992), ‘Sources of Fluctuations in Real and Nominal Exchange Rates’, Review of Economics and Statistics, 74(3), pp. 530–539.
Longworth, D. and S. Poloz (1995), ‘The Monetary Transmission Mechanism and Policy Formulation in Canada: an Overview’, in BIS, Financial Structure and the Monetary Policy Transmission Mechanism, March, pp. 312–323.
Lowe, P. and L. Ellis (1997), ‘The Smoothing of Official Interest Rates’, paper presented at this conference.
Poole, W. (1970), ‘Optimal Choice of Monetary Policy Instruments in a Simple Stochastic Macro Model’, Quarterly Journal of Economics, 84(2), pp. 197–216.
Smets, F. (1995), ‘Central Bank Macroeconometric Models and the Monetary Policy Transmission Mechanism’, in BIS, Financial Structure and the Monetary Policy Transmission Mechanism, March, pp. 225–266.
Svensson, L.E.O. (1997), ‘Inflation Forecast Targeting: Implementing and Monitoring Inflation Targets’, European Economic Review, 41(6), pp. 1111–1146.
Taylor, J.B. (1993), ‘Discretion versus Policy Rules in Practice’, Carnegie-Rochester Conference Series on Public Policy, 39, pp. 195–214.
Taylor, J.B. (1996), ‘Policy Rules as a Means to a more Effective Monetary Policy’, Institute for Monetary and Economic Studies, Bank of Japan, Discussion Paper 96-E-12.
Woodford, M. (1994), ‘Nonstandard Indicators for Monetary Policy: Can their Usefulness be Judged from Forecasting Regressions?’ in N.G. Mankiw (ed.), Monetary Policy, University of Chicago Press, Chicago, pp. 95–115.