RBA Annual Conference – 1993 Is There a Currency Bloc in the Pacific? Jeffrey A. Frankel and Shang-Jin Wei[*]
1. Introduction
The study of international economic integration – the strengthening of trade and financial links – has acquired a new geographic dimension. Now, we are curious not only about the speed or sequence with which a particular country liberalises trade and financial barriers, but also about whether it chooses to do so preferentially vis-à-vis some neighbour countries and not others.
1.1 Possible Regional Groupings
Formal regional economic arrangements have progressed the furthest in Europe. Within the European Community (EC), the Single European Act of 1986 resulted in the elimination of most trade barriers by 1992. Most members removed capital controls by 1990 and the European Monetary System (EMS) had succeeded in stabilising exchange rates well enough by December 1991 that the members agreed on ambitious plans for European Monetary Union (EMU). Those plans soon proved overly ambitious, but the long-run trend towards integration is nevertheless clear. The next successful project of the EC will most likely be enlargement to include those of the other Western European countries (members of EFTA – European Free Trade Association) who wish to join. There is also talk of eventually including countries from Central and even Eastern Europe.
In the Western Hemisphere, the Canadian-United States Free Trade Agreement took effect in 1989, the countries of the eastern half of South America agreed on plans for a free trade area under the name MERCOSUR in 1990, the moribund Andean Pact removed regional trade barriers in 1991 and the North American Free Trade Agreement (NAFTA) was negotiated in 1992. NAFTA has provisions for other countries to join, consistent with the Enterprise for the Americas Initiative proposed by the Bush Administration, with Chile considered first in line. There are no formal monetary or financial arrangements in the Western Hemisphere analogous to the EMS or the prospective EMU. Nevertheless, when a Latin American country like Argentina decides to peg its currency, the US dollar is the currency to which it pegs. Many countries are heavily dollarised de facto.
In East Asia and the Pacific, formal regional arrangements are rare. The Australia-New Zealand Closer Economic Relationship, agreed to in 1983, is a potentially useful model in that it includes some important measures such as harmonisation of competition policy that other countries have been profoundly reluctant to consider. Beyond the bilateral level, the only major plans for a Preferential Trading Arrangement (PTA) exist among the Association of South-East Asian Nations (ASEAN), which was slow to get off the ground but which, in 1991, endorsed the idea of an ASEAN Free Trade Association (AFTA).
Although Asia-Pacific is less inclined to establish intra-regional economic links through official institutions than either Europe or the Americas are, such links are nonetheless being formed in informal ways by the private sector. One view is that South China, including Hong Kong and Taiwan, is becoming an independent ‘growth pole’ deriving its dynamism from the entrepreneurial talents of the Chinese diaspora. Another view is that Japan is establishing a yen bloc in East Asia, not through preferential trading arrangements or other explicit, direct means, but rather in the way it is alleged to do everything: through implicit, indirect means, such as Foreign Direct Investment, Overseas Development Assistance, and other financial flows to the rest of Asia.
A number of loose groupings have been proposed for the region. The Malaysian Prime Minister, Dr Mahatir, suggested an East Asian Economic Group (EAEG) in 1990 (later called the East Asian Economic Caucus). The suggested boundaries of membership were drawn to include Japan, but exclude Caucasian countries. Australia had earlier proposed the Asian Pacific Economic Cooperation forum (APEC), which includes Australia, New Zealand, Canada and the United States. APEC gained steam, in part as an alternative to the EAEG. Some wish to draw the boundaries even wider, to include all countries on the Pacific Rim (most of whom, including Mexico and Chile, are represented in the membership of PECC – the Pacific Economic Cooperation Council).
1.2 Trade Links, Interest Rate Links and Currency Links
The array of acronyms is impressive. What effect have these formal and informal regional arrangements had on actual patterns of trade and finance? Empirical research on this question is relatively rudimentary. Many studies of regional trading arrangements simply report statistics on shares of intra-regional trade. It is pointed out, for example, that the fraction of East Asian countries' trade that is conducted with other East Asian countries rose from 23 per cent in 1980 to 29 per cent in 1990.[1] Yet, as we will see, these statistics can be misleading. One wants to hold constant the natural economic determinants of bilateral trade, such as proximity and gross national product (GNP), before attributing any level or increase in intra-regional trade to deliberate policy measures such as Preferential Trading Arrangements, or even to the less deliberate influences of linguistic or cultural links.
Empirical research on intra-regional financial and monetary links is even less well-developed than on trade. Most studies of financial and monetary integration examine the extent to which a particular country has become integrated with ‘the world’, for example, the extent to which unrestricted arbitrage equates its interest rate to ‘the world’ interest rate or the extent to which its monetary authorities have stabilised ‘the’ exchange rate. Less attention is paid to the question of whether the financial and monetary links are stronger with some parts of the world than others.
The remainder of this paper tries to address these issues, in relation to East Asia and the Pacific. It is divided into three parts. Section 2 examines whether a trade bloc is forming in the region and, if so, what are its geographical boundaries (ASEAN, EAEG, the Western Pacific, APEC or the entire Pacific Rim?). It extends earlier research using the gravity model by including a variable that reflects when two trading partners share a common language, such as Chinese.
Section 3 looks for evidence of a financial bloc. Specifically, it tests whether interest rates in various Pacific countries appear to be influenced more strongly by Japanese interest rates or American interest rates.
Exchange rate arrangements, considered in Section 4 of the paper, can have an important effect on the trade and financial links that are considered in Sections 2 and 3 respectively. If a country chooses to stabilise its exchange rate vis-à-vis one major trading partner instead of another, this can be expected to help promote trade with the first rather than the second, assuming that exchange rate uncertainty has a negative effect on trade. Promoting intra-EC trade, for example, is one major motivation underlying the EMS and EMU. Therefore, bilateral exchange rate variability is one more factor that we would like to control for in our econometric model of bilateral trade. Similarly, if a country chooses to stabilise its exchange rate vis-à-vis one major monetary power instead of another, this can be expected to promote financial links with the first rather than the second and to be reflected in the interest rate correlations.
2. Is There a Trade Bloc in the Pacific?
Frankel (1993) applied to the trading bloc question the natural framework for studying bilateral trade, the gravity model. The gravity model is so called because it says that trade between two countries is proportional to the product of their sizes and inversely related to the distance between them. It has a fairly long history, but there are few recent applications to a large cross-section of countries throughout the world.[2] Frankel (1993) and Frankel and Wei (1992) found that there are indeed intra-regional trade biases in the EC and the Western Hemisphere, and perhaps in East Asia. However, they also found that the greatest intra-regional bias was in none of these three, but in the APEC grouping, which includes the United States and Canada with the Pacific countries and that the bias in the East Asia and Pacific groupings did not increase in the 1980s.
This paper extends those results in a number of directions. Among various extensions of the original gravity model estimation, it tests the effect of two trading partners sharing common linguistic or historical links, with particular focus on the effect when both countries are Chinese-speaking.
2.1 The Gravity Model of Bilateral Trade
One cannot meaningfully investigate the extent to which regional policy initiatives are influencing trade patterns without holding constant natural economic determinants such as size.[3] The gravity model offers a systematic framework for measuring what patterns of bilateral trade are normal around the world. Again, the goal, is to see how much of the high level of trade within each region can be explained by simple economic factors common to bilateral trade throughout the world and how much can be attributed to a special regional effect. A dummy variable is added to the gravity equation to represent when both countries in a given pair belong to the same regional grouping. One can check how the level and time trend in, for example, ASEAN compares with that in other groupings.
The dependent variable is trade (exports plus imports), in log form, between pairs of countries in a given year. We have 63 countries in our data set, so that there are 1953 data points (=63 × 62/2) for a given year.[4] Some observations are missing because the trade flow is too small to be recorded.
One would expect the two most important factors in explaining bilateral trade flows to be the geographical distance between the two countries and their economic size.
A large part of the apparent bias toward intra-regional trade is certainly due to simple geographical proximity. Indeed Krugman (1991) suggests that most of it may be due to proximity, so that the three trading blocs are welfare-improving ‘natural’ groupings (as distinct from ‘unnatural’ trading arrangements between distant trading partners such as the United Kingdom and a Commonwealth member, or the United States and an East Asian dragon). Despite the obvious importance of distance and transportation costs in determining the volume of trade, surprisingly, empirical studies often neglect to measure this factor. Our measure is the log of the distance between two major cities (usually the capital) of the respective countries. We also add a dummy ‘adjacent’ variable to indicate when two countries share a common land border.
Entering GNPs in product form is empirically well established in bilateral trade regressions. It can be justified by the modern theory of trade under imperfect competition.[5] In addition, there is reason to believe that GNP per capita has a positive effect on trade; for a given size, as countries become more developed, they tend to specialise more and to trade more. Equivalently, size as measured by population has a negative effect on openness to trade, expressed as a share of GNP. The equation to be estimated, in its most basic form, is:
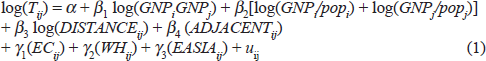
The last four explanatory factors are dummy variables. EC, WH, and EASIA are three of the dummy variables we use when testing the effects of membership in a common regional grouping, representing the European Community, Western Hemisphere, and East Asian Economic Group, respectively.
Results are reported in Table 1. These differ from the tables in Frankel (1993) and Frankel and Wei (1992) by a doubling of the span of years reported (among other things). All four standard variables are highly significant statistically (greater than the 99 per cent level) in every year . The adjacency variable indicates that when two countries share a common border, they trade with each other approximately twice as much as they would otherwise [exp(0.7)=2]. The coefficient on the log of distance is about −0.5, holding constant for the adjacency variable. This means that when the distance between two non-adjacent countries is higher by 1 per cent, the trade between them falls by about 0.5 per cent. We have tested for possible non-linearity in the log-distance term, as it could conceivably be the cause of any apparent bias toward intra-regional trade that is left after controlling linearly for distance.[6]
| 1965 | 1970 | 1975 | 1980 | 1985 | 1990 | |
|---|---|---|---|---|---|---|
| GNP | 0.64** (0.02) |
0.64** (0.02) |
0.72** (0.02) |
0.74** (0.02) |
0.54** (0.02) |
0.76** (0.02) |
| GNP per capita | 0.27** (0.02) |
0.37** (0.02) |
0.27** (0.02) |
0.30** (0.02) |
0.07** (0.02) |
0.10** (0.02) |
| Distance | −0.43** (0.04) |
−0.52** (0.04) |
−0.67** (0.05) |
−0.54** (0.04) |
−0.35** (0.05) |
−0.54** (0.04) |
| Adjacency | 0.52** (0.17) |
0.58** (0.17) |
0.47** (0.18) |
0.63** (0.18) |
0.69** (0.20) |
0.74** (0.16) |
| WH2 | −0.34* (0. 16) |
−0.19 (0.14) |
0.10 (0.15) |
0.34* (0.15) |
0.38* (0.19) |
0.82** (0.14) |
| EAEG2 | 1.59** (0.29) |
1.80** (0.29) |
0.96** (0.31) |
0.93** (0.26) |
−0.27 (0.28) |
0.75** (0.24) |
| EC2 | 0.28# (0.16) |
0.12 (0.17) |
−0.03 (0.18) |
0.27 (0.18) |
1.58** (0.19) |
0.54** (0.16) |
| APEC2 | 0.37# (0.21) |
0.64** (0.21) |
0.85** (0.22) |
1.29** (0.18) |
1.39** (0.20) |
1.19** (0.17) |
| Common language |
0.50** (0.09) |
0.33** (0.09) |
0.33** (0.09) |
0.52** (0.08) |
0.53** (0.10) |
0.35** (0.08) |
| Number of observations | 1,194 | 1,274 | 1,453 | 1,708 | 1,343 | 1,573 |
| SEE | 1.05 | 1.07 | 1.17 | 1.19 | 1.26 | 1.06 |
| adj. R2 | 0.68 | 0.71 | 0.72 | 0.72 | 0.53 | 0.77 |
| Notes: (a) Standard errors are in parentheses. (b) ** denotes significance at 1% level (t 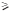 2.576); 2.576);* denotes significance at 5% level (t 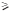 1.96); and 1.96); and# denotes significance at 10% level (t 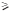 1.645). 1.645).(c) All variables except the dummies are in logarithms. (d) Common language is the dummy for common linguistic or colonial links (German, Japanese, Dutch, English, Spanish, Chinese, Arabic, French and Portugese). |
||||||
The estimated coefficient on GNP per capita is about 0.3 from 1965 through 1980, indicating that richer countries do indeed trade more, though this term declines during the 1980s, reaching 0.1 in 1990.[7] The estimated coefficient for the log of the product of the two countries' GNPs is about 0.75, indicating that, though trade increases with size, it increases less than proportionately (holding GNP per capita constant). This presumably reflects the widely known pattern that small economies tend to be more open to international trade than larger, more diversified economies. At the same time, the equation explains why worldwide trade has historically increased faster than GNP.[8] If two countries are each experiencing growth in GNP per capita of 1 per cent a year, then trade between them will grow at about 2 per cent a year (1.05 + 1.05 = 2.1). As East Asian developing countries have recently been growing in the vicinity of 8 per cent a year, the equation predicts very rapid growth in trade among them (16 per cent).
We have recently added a few checks for econometric robustness regarding the sample of countries and their size. We also tried running the equation in multiplicative form, instead of log-linear form, to allow the inclusion of pairs of countries that are reported as undertaking zero trade. (Under the log-linear specification, any pair of countries that shows up with zero trade must necessarily be dropped from the sample.) We find that the inclusion or omission of such countries in the multiplicative specification makes little difference to the results.[9] A correction for heteroscedasticity based on the size of the countries also makes little difference.
2.2 Estimation of Trade Bloc Effects
If there was nothing to the notion of trading blocs, then the four or five basic variables would soak up most of the explanatory power. There would be little left to attribute to a dummy variable representing whether two trading partners are both located in the same bloc. In this case, the level and trend in intra-regional trade would be due solely to the proximity of the countries, and to their rate of overall economic growth.
However, we have found that dummy variables for intra-regional trade are highly significant statistically. If two countries are both located in East Asia, for example, in 1980 they traded with each other by an estimated two and a half times as much as they would have otherwise [exp(0.9) = 2.5], after taking into account distance and the other gravity variables.
In earlier results, we tested for a nested sequence of possible trading blocs: ASEAN, East Asia (the membership of the EAEG), the Asian Pacific (including also Australia and New Zealand), APEC (including also the United States and Canada), and the entire Pacific Rim (including also Mexico, Colombia, Ecuador, Peru and Chile). While groupings such as ASEAN or the Asian Pacific can appear to be statistically significant if one does not test for larger groupings at the same time, there appear to be two right places to draw the boundaries: around East Asia and around APEC. The smaller and larger groupings are not statistically significant when these two are included in the equation. (For one year, 1985, the presence of the APEC term reduces or eliminates the significance of the East Asia term.)
To see if the East Asian bloc can be interpreted as Japan-centred, we included a dummy variable representing Japan's bilateral trade with other East Asian countries. It was not statistically significant (or even greater than zero). We also tried allowing for a special entrêpot effect by including a dummy variable representing all bilateral trade of either Singapore or Hong Kong. The entrêpot variable is highly significant, but does little to diminish the East Asian bloc effect.[10] When one allows for the greater average openness of East Asian countries to trade with all partners, the East Asian bloc effect does diminish somewhat, but is still statistically significant.[11]
We have also tried to capture classic Heckscher-Ohlin effects. Earlier we tried including bilateral absolute differences in GNP per capita figures. The variable did not have the positive effect that one might think if countries traded capital-intensive products for products intensive in unskilled labor. Rather, it had a moderately significant negative effect, as in the Linder hypothesis that similar countries trade more than dissimilar ones.
The gravity model was estimated including some direct measures of factor endowments: the two countries' differences in capital/labor ratios, educational attainment levels, and land/labor ratios. The data (for a subset of 656 of our 1953 pairs of countries) was generously supplied by Saxonhouse (1989). Most of the coefficients were little affected.
As another extension, we tried disaggregating total trade into three categories: manufactured products, agricultural products, and other raw materials. Perhaps surprisingly, the effect of distance is as high (or higher) for manufactures as for the other categories. But in general, the findings were little affected by the disaggregation.[12]
Although the coefficient for the East Asian grouping in Table 1 is significant, it diminishes in the 1980s, rather than increasing as is often assumed on the basis of simple statistics on intra-regional trade. The explanation for this is that rapid growth of East Asian economies is, in itself, sufficient to explain the increase in the intra-regional trade share mentioned in the introduction. The extension of the time period back to 1965 reveals that the trend in the intra-regional trade bias has been, if anything, downward rather than upward throughout this period.[13] Also, as in earlier results, the strongest grouping in the world in the 1980s was APEC. East Asia is still dependent on the North American market.
Inferences about Europe and the Western Hemisphere, like inferences about East Asia, are overturned with the use of the gravity model in place of intra-regional trade shares. It turns out that the EC was not a statistically significant trade bloc as recently as 1980, but that in the first half of the 1980s it experienced the most rapid intensification of intra-regional trade bias of any region. (The EFTA countries show no trade bloc effect at any time.)[14] The Western Hemisphere countries show the most rapid intensification of intra-regional trade bias in the second half of the 1980s. More detailed analysis reveals that this regionalisation took place in particular within MERCOSUR and within the Andean Pact.[15]
2.3 Extension: the Role of Common Language in Trade Groupings
Now we extend the results by adding a dummy variable to represent when a pair of countries share a common language or had colonial links earlier in the century. We allow for English, Spanish, Chinese, Arabic, French, German, Japanese, Dutch and Portuguese. The results, reported in Table 1, show a significant coefficient that fluctuates in the range of 0.33 to 0.53. In 1990, two countries sharing such linguistic or colonial links tended to trade roughly 42 per cent more than they would otherwise [exp(0.35)=1.42]. We tested whether some of the major languages were more important than the others.[16] Chinese is the one language to qualify, though even here, the independent effect is significant only in 1970 and 1990. (We count four countries as primarily Chinese speaking: Taiwan, China, Hong Kong and Singapore.) Its independent effect is reported in Table 2. As of 1990, two Chinese-speaking countries appear to trade an estimated four and one-half times as much [exp(0.33+1.2=1.53)=4.62] as other similarly situated countries.
| 1965 | 1970 | 1975 | 1980 | 1985 | 1990 | |||
|---|---|---|---|---|---|---|---|---|
| GNP | 0.64** (0.02) |
0.64** (0.02) |
0.72** (0.02) |
0.74** (0.02) |
0.54** (0.02) |
0.76** (0.02) |
||
| GNP per capita | 0.27** (0.02) |
0.37** (0.02) |
0.27** (0.02) |
0.30** (0.02) |
0.06** (0.02) |
0.10** (0.02) |
||
| Distance | −0.44** (0.04) |
−0.53** (0.04) |
−0.67** (0.05) |
−0.54** (0.04) |
−0.35** (0.05) |
−0.54** (0.04) |
||
| Adjacency | 0.51** (0.17) |
0.59** (0.17) |
0.47** (0.18) |
0.62** (0.18) |
0.69** (0.20) |
0.73** (0.16) |
||
| WH2 | −0.33* (0.16) |
−0.19 (0.14) |
0.10 (0.15) |
0.35* (0.15) |
0.39* (0.19) |
0.83** (0.14) |
||
| EAEG2 | 1.50** (0.29) |
1.67** (0.30) |
0.92** (0.31) |
0.85** (0.27) |
−0.36 (0.29) |
0.60** (0.24) |
||
| EC2 | 0.28# (0.16) |
0.11 (0.17) |
−0.03 (0.18) |
0.27 (0.18) |
1.58** (0.19) |
0.54** (0.16) |
||
| APEC2 | 0.38# (0.21) |
0.65** (0.21) |
0.85** (0.22) |
1.29** (0.18) |
1.40** (0.20) |
1.19** (0.17) |
||
| Common language |
0.48** (0.09) |
0.31** (0.09) |
0.32** (0.09) |
0.50** (0.08) |
0.51** (0.10) |
0.33** (0.08) |
||
| Chinese | 0.80 (0.56) |
1.94* (0.79) |
0.58 (0.86) |
0.71 (0.57) |
0.77 (0.60) |
1.21* (0.51) |
||
| Number of observations | 1,194 | 1,274 | 1,453 | 1,708 | 1,343 | 1,573 | ||
| SEE | 1.05 | 1.07 | 1.17 | 1.19 | 1.26 | 1.06 | ||
| adj. R2 | 0.69 | 0.71 | 0.72 | 0.72 | 0.53 | 0.77 | ||
| Notes: (a) Standard errors are in parentheses. (b) ** denotes significance at 1% level (t 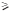 2.576); 2.576);* denotes significance at 5% level (t 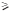 1.96); and 1.96); and# denotes significance at 10% level (t 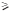 1.645). 1.645).(c) All variables except the dummies are in logarithms. (d) Common language is the dummy for common linguistic or colonial links (German, Japanese, Dutch, English, Spanish, Chinese, Arabic, French and Portugese). |
||||||||
The presence of the language terms reduces the East Asian bloc coefficient only slightly; in most years the latter is still highly significant statistically. The apparent magnitude of the Chinese language term does raise the possibility that the influence of the Chinese diaspora is a more important contributor to the East Asian intra-regional trade than is the influence of ‘Japan Inc’. However, there is an important objection that must be registered. Taiwan-China trade does not appear in the statistics, because it is officially non-existent. Such trade is in reality thought to be large and rapidly growing and heavily to take the form of trade routed indirectly through Hong Kong. If Taiwan-China trade is routed through Hong Kong (or Singapore), then it is counted twice in our data and thus may be exaggerating the estimate of the influence of the Chinese variable.
We now attempt to correct for this double-counting of Taiwan-China trade. The Governments of Taiwan and China each report estimates of their true bilateral trade. To err on the side of caution, we took the larger of the estimates and treated it as if it were all counted twice in the form of Hong Kong trade. The numbers were $0.047 billion in 1980 and $1.974 billion in 1990. (The Governments report no estimate for 1985, but we took the average of the other two years.) We re-ran the gravity estimates with trade among ‘the three Chinas’ adjusted in this way. The results, reported in Table 3, show that the independent Chinese language effect is no longer statistically significant. Even the East Asian bloc coefficient is reduced slightly. However, the dummy variable for linguistic links, in general, is as strong as ever. Given the small number of observations of Chinese-speaking pairs of countries (4 × 3/2 = 6), we are left without a clear verdict one way or the other on the importance of the contribution of the Chinese diaspora effect to intra-regional trade.
| 1980 | 1985 | 1990 | 1980 | 1985 | 1990 | |
|---|---|---|---|---|---|---|
| GNP | 0.74** (0.02) |
0.54** (0.02) |
0.71** (0.02) |
0.70** (0.02) |
0.56** (0.02) |
0.71** (0.02) |
| GNP per capita | 0.30** (0.02) |
0.07** (0.02) |
0.08** (0.02) |
0.29** (0.02) |
0.07** (0.02) |
0.08** (0.02) |
| Distance | −0.54** (0.04) |
−0.37** (0.05) |
−0.50** (0.05) |
−0.46** (0.04) |
−0.38** (0.05) |
−0.50** (0.04) |
| Adjacency | 0.65** (0.18) |
0.65** (0.20) |
0.72** (0.18) |
0.56** (0.17) |
0.64** (0.20) |
0.72** (0.16) |
| WH2 | 0.35* (0.15) |
0.39* (0.19) |
0.78 (0.15) |
0.36* (0.16) |
0.40* (0.19) |
0.78** (0.15) |
| EAEG2 | 0.84** (0.26) |
−0.26 (0.28) |
0.62** (0.31) |
0.85** (0.24) |
−0.38 (0.29) |
0.55* (0.22) |
| EC2 | 0.27 (0.18) |
1.55** (0.19) |
0.59** (0.18) |
0.29# (0.16) |
1.51** (0.19) |
0.59** (0.15) |
| APEC2 | 1.29** (0.18) |
1.39** (0.20) |
1.12** (0.22) |
1.04** (0.16) |
1.37** (0.20) |
1.12** (0.15) |
| Common language |
0.50** (0.08) |
0.54** (0.10) |
0.32** (0.09) |
0.62** (0.09) |
0.56** (0.10) |
0.30** (0.08) |
| Chinese | −0.41 (0.55) |
1.15# (0.66) |
0.65 (0.51) |
|||
| Number of observations | 1,709 | 1,324 | 1,259 | 1,259 | 1,259 | 1,259 |
| SEE | 1.20 | 1.26 | 0.95 | 1.03 | 1.25 | 0.95 |
| adj. R2 | 0.72 | 0.53 | 0.77 | 0.72 | 0.54 | 0.77 |
| Notes: (a) Standard errors are in parentheses. (b) ** denotes significance at 1% level (t 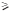 2.576); 2.576);* denotes significance at 5% level (t 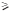 1.96); and 1.96); and# denotes significance at 10% level (t 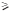 1.645). 1.645).(c) All variables except the dummies are in logarithms. (d) Common language is the dummy for common linguistic or colonial links (German, Japanese, Dutch, English, Spanish, Chinese, Arabic, French and Portugese). |
||||||
3. Is There a Financial Bloc in the Pacific?
Those who believe that Japan is establishing an economic bloc in Asia often describe it as a ‘yen bloc’, which carries a financial/monetary connotation. We turn now from trade to financial effects.
We seek to investigate the extent to which Pacific financial markets are becoming more tightly linked, by analysing interest rates in a number of countries around the Pacific. International equalisation of interest rates would be an important phenomenon for many reasons. It would imply, for example, that national monetary authorities had lost the ability to affect domestic demand through independent monetary policies and that countries would easily be able to finance investments despite savings shortfalls. Earlier studies of interest rate parity issues in the Pacific context include Glick (1987) and Glick and Hutchison (1990). A number of studies have found evidence of financial liberalisation in some Pacific countries by observing the ability of international arbitrage to link local interest rates with United States rates. Here we focus on the question: to the extent that interest rates in Pacific countries are now influenced by interest rates in world financial centres, is the power of Tokyo in the region gaining over that of New York?[17]
We tried three tests of the relative influence of Tokyo and New York financial markets, corresponding to more standard tests of simple interest rate parity, covered interest parity, and uncovered interest parity. We regressed:
- the local interest rate on the United States and Japanese interest rates (and on these interest rates interacted with a linear time trend);
- the local rate on the covered counterparts of (i); and
- the local rate on the uncovered counterparts of (i).
If the world's financial markets and monetary systems are perfectly integrated, then we should not expect to be able to sort out any bilateral effects, such as from Japan to smaller countries in the region. Rather, countries would simply deposit savings into, or draw funds out of, an undifferentiated pool of world capital. But few countries in the Pacific follow a perfectly pegged exchange rate, and the majority still have serious barriers to capital mobility as well.[18] Even capital mobility between the United States and Japan faces minor frictions and major exchange rate uncertainty. Thus, we may be able to pick up some differential effects of New York and Tokyo interest rates in the region.
3.1 The Influence of US Dollar versus Yen Interest Rates
The results of the first test are reported in Table 4.[19] The coefficients on the interaction terms can be interpreted as the increase per year (on average) of the coefficient relating the local interest rate to the corresponding US or Japanese interest rate. All the regressions exhibit a high degree of serial correlation, so the adjusted standard errors are the appropriate ones to use in conducting inference. One finding is that, in almost every case, the trend coefficients are of opposite sign, suggesting that one financial centre is gaining at the expense of another. However, since the relevant parameter estimates are not always statistically significant, one cannot make too much of this result.
| Constant | Eurodollar | Eurodollar trend | Euroyen | Euroyen trend | R2 | DW | Q | |
|---|---|---|---|---|---|---|---|---|
| Australia | 8.473* | −1.992** | 0.429** | 3.470** | −0.539** | 0.52 | 0.409 | 141.47** |
| (1.143) | (0.277) | (0.041) | (0.411) | (0.054) | ||||
| [3.428] | [0.479] | [0.071] | [0.712] | [0.094] | ||||
| Canada | 0.535 | 0.487* | 0.086** | 0.670* | −0.057 | 0.79 | 0.477 | 158.12** |
| (0.458) | (0.111) | (0.016) | (0.165) | (0.022) | ||||
| [1.375] | [0.192] | [0.028] | [0.285] | [0.038] | ||||
| Hong Kong | −4.115 | 1.691** | −0.068 | −0.353 | 0.104 | 0.71 | 1.047 | 41.35** |
| (0.857) | (0.208) | (0.031) | (0.308) | (0.041) | ||||
| [2.570] | [0.360] | [0.053] | [0.533] | [0.071] | ||||
| Indonesia | 14.010** | 1.852** | −0.267** | −2.337* | 0.410** | 0.33 | 0.700 | na |
| (1.483) | (0.356) | (0.053) | (0.529) | (0.070) | ||||
| [4.449] | [0.616] | [0.091] | [0.916] | [0.121] | ||||
| Korea 1 | 9.094** | −0.037 | −0.031* | −0.103 | 0.002 | 0.82 | 0.488 | 124.18** |
| (0.194) | (0.039) | (0.009) | (0.065) | (0.011) | ||||
| [0.581] | [0.067] | [0.015] | [0.113] | [0.019] | ||||
| Korea 2 | 16.294** | −0.754 | 0.097 | −0.929 | 0.086 | 0.64 | 0.671 | 57.01** |
| (1.087) | (0.527) | (0.077) | (0.704) | (0.091) | ||||
| [3.262] | [0.913] | [0.133] | [1.219] | [0.158] | ||||
| Korea 3 | 10.079** | 0.320 | −0.061 | −0.019 | 0.124* | 0.69 | 0.204 | 194.35** |
| (0.690) | (0.143) | (0.026) | (0.231) | (0.031) | ||||
| [2.070] | [0.248] | [0.045] | [0.400] | [0.053] | ||||
| Malaysia | 5.520 | −0.057 | −0.072 | 0.700 | 0.016 | 0.41 | 0.463 | na |
| (1.262) | (0.286) | (0.049) | (0.453) | (0.059) | ||||
| [3.785] | [0.496] | [0.086] | [0.784] | [0.102] | ||||
| New Zealand | 18.573** | −2.584** | 0.379** | 3.405** | −0.599** | 0.37 | 0.327 | 204.22** |
| (2.063) | (0.500) | (0.074) | (0.742) | (0.098) | ||||
| [6.291] | [0.866] | [0.129] | [1.285] | [0.169] | ||||
| Singapore | −2.768* | 0.960** | −0.052* | 0.174 | 0.056 | 0.86 | 0.842 | 103.64** |
| (0.413) | (0.093) | (0.014) | (0.142) | (0.019) | ||||
| [1.239] | [0.161] | [0.025] | [0.246] | [0.032] | ||||
| Taiwan | −4.144 | 0.635 | 0.017 | 0.811 | 0.049 | 0.45 | 0.422 | 109.01** |
| (1.217) | (0.292) | (0.043) | (0.437) | (0.057) | ||||
| [3.651] | [0.505] | [0.075] | [0.757] | [0.099] | ||||
| Thailand | −3.846 | 0.780 | −0.069 | 1.363* | 0.097 | 0.78 | 0.461 | na |
| (1.114) | (0.232) | (0.039) | (0.363) | (0.049) | ||||
| [3.341] | [0.402] | [0.068] | [0.628] | [0.085] | ||||
| Notes: (a) Figures in parentheses (.) are asymptotic standard errors; figures
in brackets [.] are standard errors assuming N/3 independent observations. (b) Q statistic indicates the Ljung-Box Q statistic. (c) ** denotes significance at 1% level (using adjusted standard errors); * denotes significance at 5% level (using adjusted standard errors). |
||||||||
Perhaps the most interesting finding is that over the 1982–92 period, New York seems to be gaining influence at the expense of Tokyo in the English-speaking countries of the Pacific Rim (Australia, Canada and New Zealand), while the reverse is occurring in a number of East Asian countries. The observed shift in influence from New York interest rates to Tokyo interest rates is highly significant in the case of Indonesia and somewhat less so in the case of Korea. It is positive but not significant for Malaysia, Singapore and Hong Kong.
3.2 The Influence of United States' versus Japanese Interest Rates, with Currency Factors Removed
It is interesting to try to distinguish whether the links to Tokyo and New York are attributable to country-specific factors on the one hand, such as information advantages that might be afforded by common cultures or tax and legal systems, or to currency factors on the other hand, such as the weights of the yen and United States dollar ($US) in a country's currency basket. To the extent that an Asian currency is linked to the yen or $US, currency factors such as expectations of depreciation or an exchange risk premium should disappear from the interest rate equation. (We will be looking at the currency links directly in terms of exchange rates in the next section of the paper.)
We tried, in two different ways (‘covered’ and ‘uncovered’), to remove the currency factors from the interest rate regressions, to see what remains. Unfortunately, data are not available for some of the countries in Table 4, including Indonesia. We regressed the local interest rate on both the covered United States and covered Japanese interest rates, where the cost of cover is observed in the forward exchange market, with the aim of discerning country-specific links. There is strong a priori reason to expect high multicollinearity, since covered interest parity holds fairly well between $US and yen interest rates.[20] Thus, it should not be very surprising that none of the interaction parameter estimates is statistically significant.[21] The two that are almost significant, Malaysia and Singapore, continue to indicate that influence is shifting from New York to Tokyo.
We also tested the effect of uncovered United States' and Japanese interest rate results, using survey data to measure expectations regarding future exchange rates. The survey data are from Currency Forecasters' Digest, which reports forecasts of market participants (actually the harmonic mean of the responses) on a monthly basis.[22] There is evidence of declining New York influence in Canada, and increasing influence of New York in Korea. The sign on the Tokyo term suggests that influence is shifting there for a majority of the six countries, but most are not statistically significant. Here, the destroyer of statistical significance is probably measurement error in the survey data, rather than the less serious disease of multicollinearity.
4. Currency Blocs
As already noted, the phrase ‘yen bloc’ connotes Japanese monetary influence in Pacific Asia. Such a trend would certainly round out the symmetry of the three blocs, as the $US is dominant in the Western Hemisphere and the deutschemark (DM) in Europe. But, as with trade, formal currency links are missing in East Asia. No currency is pegged to the yen, for example. Are informal currency links forming between Japan and other East Asian countries?
4.1 Stabilisation of Exchange Rates within the Blocs
Consider bilateral exchange rate variability, computed in Table 5. Worldwide, monthly exchange rate variability rose in the 1980s, from a standard deviation of 0.33 per cent in 1980 to 0.38 per cent in 1990. The latter figure suggests that for a typical pair of countries, approximately 95 per cent of exchange rate changes are smaller than 0.76 per cent (two standard deviations, under the simplifying assumption of a log-normal distribution).
| ‘Entire World‘ | (63 countries) | |
|---|---|---|
| 80 | 0.00333 | |
| 85 | 0.00390 | |
| 90 | 0.00375 | |
| Western Hemisphere | Among Members | With the Rest of the World |
| Number of observations: | 36 | 344 |
| 80 | 0.000821 | 0.00231 |
| 85 | 0.00891 | 0.00757 |
| 90 | 0.00920 | 0.00636 |
| EC | Among Members | With the Rest of the World |
| Number of observations: | 45 | 375 |
| 80 | 0.000504 | 0.00233 |
| 85 | 0.000516 | 0.00255 |
| 90 | 0.000187 | 0.00241 |
| EFTA | Among Members | With the Rest of the World |
| Number of observations: | 15 | 239 |
| 80 | 0.000398 | 0.00215 |
| 85 | 0.000198 | 0.00226 |
| 90 | 0.000210 | 0.00222 |
| Europe | Among Members | With the Rest of the World |
| Number of observations: | 105 | 527 |
| 80 | 0.000445 | 0.00244 |
| 85 | 0.000398 | 0.00265 |
| 90 | 0.000206 | 0.00254 |
| EAEG | Among Members | With the Rest of the World |
| Number of observations: | 15 | 237 |
| 80 | 0.001028 | 0.00234 |
| 85 | 0.000726 | 0.00221 |
| 90 | 0.000445 | 0.00235 |
| APEC | Among Members | With the Rest of the World |
| Number of observations: | 28 | 308 |
| 80 | 0.000834 | 0.00229 |
| 85 | 0.000608 | 0.00221 |
| 90 | 0.000394 | 0.00240 |
There is a tendency for exchange rate variability to be lower within each of the groups than across groups, supporting the idea of currency blocs. The lowest variability occurs within Europe. The 1980 statistic is a standard deviation of 0.04 per cent, and it falls by half during the course of the decade.
The members of APEC also have a relatively low level of intra-regional exchange rate variability, especially in light of the diversity of the countries involved. It too fell by half in the course of the 1980s. The level of exchange rate variability is a bit higher within East Asia considered alone. As we shall see, this reflects the fact that the international currency of Asia is not the yen, but the $US.
The Western Hemisphere considered alone shows much higher levels of exchange rate variability than any of the other groupings.
4.2 The Influence of the US Dollar, Yen, Deutschemark and Pound on the Values of Smaller Currencies in the Pacific
We now examine the influences which the four most important international currencies have on the determination of the values of currencies of smaller countries in Pacific Asia. One way that countries in a given area could achieve the lower levels of intra-regional bilateral exchange rate variability noted above is to link their currencies to the single most important currency in the region. In a simple version of the currency bloc hypothesis, one would expect that the $US has dominant influence in the Western Hemisphere, the yen in East Asia and the DM (or ECU) in Europe.
The equation to be estimated is:
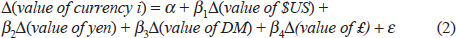
where the change in the value of each currency is computed logarithmically. The goal is to see whether Pacific Asian countries try to stabilise their currencies in terms of a particular major currency. Such an equation is exceptionally well specified under a particular null hypothesis, namely that the value of the local currency is determined as a basket peg (perhaps a crawling peg, since we allow for a constant term). By ‘exceptionally well specified’, we mean that the coefficients should be highly significant and the R2 should be close to 1.
In 1988, for example, there were 31 countries that were officially classified by the International Monetary Fund (IMF) as following a basket peg of their own design, plus another eight pegged to the SDR (Special Drawing Rights). They included Austria, Finland, Norway, Sweden, Iceland and Thailand. Others, such as Korea, claimed to define the value of their currency in terms of a basket, but in fact followed an extremely loose link. Most basket-peggers keep the weights in the basket secret, so that one can only infer the weight statistically from observed exchange rate movements. Previous tests have suggested that countries that are officially classified as basket-peggers in practice often exhibit a sufficiently wide range of variation around the basket index, or else alter the parity or weights sufficiently often, that they are difficult to distinguish from countries classified as managed floaters.[23]
In applying equation (2) to a wide variety of countries, we realise that most do not follow a basket peg. If policy makers monitor an index which is a weighted average of their trading partners, even though they allow deviations from the index depending on current macroeconomic considerations or speculative sentiments, we can meaningfully estimate the coefficients in the equation under the (restrictive) assumption that these local deviations – the error term – are uncorrelated with the values of the major currencies.
There is a methodological question of what numeraire should be used to measure the value of the currencies. Preliminary results on the determination of exchange rates tried two numeraires: the Swiss franc and purchasing power over local goods.[24] The results, for nine East Asian countries, suggested that all place very heavy weight on the $US in their implicit baskets. Only Singapore and Indonesia, and at times Malaysia and Thailand, appear to put significant weight on the yen, and the weight is usually less than 0.1, as against 0.9 to 1.0 on the $US.
Here we use the SDR as numeraire. Under the basket-peg null hypothesis, the choice of numeraire makes no difference in the estimation of the weights. But more generally, it will make a difference. We also impose the constraint that the sum of the coefficients adds to one (with the pound sterling treated as the residual in the reported results).
In Europe almost all countries give dominant weight to the major currency of the region: the DM.[25] In the Americas, most currencies tested again give dominant weight to the major regional currency, the $US (Table 6). In the results of Table 7, however, we see that this pattern is broken in East Asia. The weight on the $US is very high in Thailand, Korea and China. There is no special role for the yen. The Japanese currency is statistically significant in Singapore, and occasionally in some of the other countries. But the coefficient is low. The same is true of the DM and pound sterling (which are significant, for example, in Singapore). Each of the Asian countries is more properly classed in a dollar bloc than in a yen bloc. It is not a coincidence that many Asian/Pacific countries call their currencies ‘dollar’. Nor, given the economies of scale in the use of an international currency, is it surprising that the $US is the first choice of Asia when it comes to such measures as shares of official reserve holdings, invoicing of trade and denomination of international financial transactions, as it is the first choice of the rest of the world.
| Time Period | Constant | $US | Yen | DM | adj.R2/DW | Number of Obs. | SEE |
|---|---|---|---|---|---|---|---|
| Canada-Dollar | |||||||
| 79.1–82.12 | −0.001 (0.002) |
0.679** (0.072) |
0.021 (0.057) |
0.126# (0.071) |
0.072/1.89 | 47 | 0.013 |
| 83.1–86.12 | −0.002## (0.001) |
0.883** (0.049) |
0.011 (0.069) |
−0.010 (0.068) |
0.467/1.97 | 48 | 0.009 |
| 87.1–90.12 | −0.003# (0.002) |
0.974** (0.058) |
−0.036 (0.085) |
0.541 (0.099) |
0.535/2.17 | 48 | 0.012 |
| 79.1–90.12 | 0.000 (0.001) |
0.867** (0.034) |
−0.020 (0.038) |
0.054 (0.045) |
0.346/2.08 | 143 | 0.012 |
| Mexico-Peso | |||||||
| 79.1–82.12 | −0.031# (0.018) |
1.220# (0.652) |
−0.610 (0.510) |
−0.429 (0.643) |
0.004/1.65 | 47 | 0.120 |
| 83.1–86.12 | −0.045** (0.004) |
1.477** (0.153) |
−0.039 (0.213) |
−0.476* (0.210) |
0.485/1.83 | 48 | 0.027 |
| 87.1–90.12 | −0.023** (0.005) |
1.333** (0.166) |
−0.547* (0.246) |
−0.127 (0.286) |
0.309/1.22 | 48 | 0.036 |
| 79.1–90.12 | −0.032** (0.001) |
1.414** (0.025) |
−0.467* (0.028) |
−0.361 (0.033) |
0.104/1.99 | 143 | 0.017 |
| Argentina-Peso | |||||||
| 79.1–82.12 | −0.003# (0.002) |
0.280** (0.066) |
0.097# (0.051) |
0.489** (0.065) |
0.463/1.37 | 47 | 0.012 |
| 83.1–86.12 | −0.004* (0.002) |
0.066 (0.072) |
0.129 (0.100) |
0.583** (0.099) |
0.485/1.83 | 48 | 0.014 |
| 87.1–90.12 | 0.001 (0.001) |
0.281** (0.039) |
0.077 (0.058) |
0.434** (0.067) |
0.523/1.60 | 48 | 0.008 |
| 79.1–90.12 | −0.002* (0.001) |
0.198** (0.033) |
0.083* (0.037) |
0.529** (0.043) |
0.568/1.99 | 143 | 0.012 |
| Chile-Escudo | |||||||
| 79.1–82.12 | −0.015* (0.007) |
0.848** (0.258) |
0.060 (0.202) |
0.054 (0.255) |
−0.016/1.45 | 47 | 0.047 |
| 83.1–86.12 | −0.022** (0.006) |
0.917** (0.209) |
−0.034 (0.292) |
0.224 (0.288) |
0.030/2.06 | 48 | 0.039 |
| 87.1–90.12 | −0.010** (0.002) |
1.063** (0.063) |
−0.032 (0.093) |
0.247* (0.108) |
0.572/1.63 | 48 | 0.013 |
| 79.1–90.12 | −0.016** (0.003) |
0.929** (0.100) |
0.016 (0.112) |
0.035 (0.131) |
0.083/1.68 | 143 | 0.036 |
| Colombia-Peso | |||||||
| 79.1–82.12 | −0.011** (0.001) |
0.986** (0.021) |
−0.049** (0.017) |
0.024 (0.021) |
0.913/0.71 | 47 | 0.004 |
| 83.1–86.12 | −0.024** (0.001) |
1.090** (0.039) |
−0.010 (0.055) |
0.017 (0.054) |
0.821/0.79 | 48 | 0.007 |
| 87.1–90.12 | 0.020** (0.000) |
0.971** (0.015) |
0.063** (0.022) |
0.006 (0.026) |
0.948/0.60 | 48 | 0.003 |
| 79.1–90.12 | −0.018** (0.001) |
1.041** (0.021) |
−0.018 (0.023) |
−0.950 (0.028) |
0.787/0.28 | 143 | 0.008 |
| Notes (a) Standard errors are in parenthesis. (b) All currencies are measured in terms of SDR ($US 0.42, DM 0.19, yen 0.15, French franc 0.12, pound sterling 0.12). (c) **, *, # and ##, denote statistical significance at the 99%, 95%, 90%, 85% levels, respectively. |
|||||||
| Time Period | Constant | $US | Yen | DM | adj.R2/DW | Number of Obs. | SEE |
|---|---|---|---|---|---|---|---|
| Singapore-Dollar | |||||||
| 79.1–82.12 | −0.003# (0.001) | 0.549** (0.050) |
0.130** (0.039) |
0.231** (0.049) |
0.354/2.19 | 47 | 0.009 |
| 83.1–86.12 | −0.003 (0.002) | 0.697** (0.066) |
0.275** (0.092) |
−0.035 (0.091) | 0.324/2.10 | 48 | 0.012 |
| 87.1–90.12 | −0.003** (0.001) |
0.752** (0.039) |
0.082 (0.058) | 0.081 (0.067) | 0.366/1.95 | 48 | 0.008 |
| 79.1–90.12 | 0.010 (0.001) | 0.696** (0.030) |
0.132** (0.033) |
0.117** (0.039) |
0.270/2.05 | 143 | 0.011 |
| Thailand-Baht | |||||||
| 79.1–82.12 | −0.002 (0.002) | 0.878** (0.072) |
0.056 (0.057) | 0.015 (0.071) | 0.378/2.08 | 47 | 0.011 |
| 83.1–86.12 | −0.004 (0.004) | 0.756** (0.131) |
0.082 (0.183) | 0.124 (0.180) | 0.028/2.10 | 48 | 0.025 |
| 87.1–90.12 | −0.000 (0.000) | 0.807** (0.007) |
0.127 (0.011) | 0.44** (0.013) |
0.970/2.55 | 48 | 0.002 |
| 79.1–90.12 | −0.002 (0.001) | 0.806** (0.045) |
0.073## (0.049) | 0.062 (0.058) | 0.228/2.09 | 143 | 0.016 |
| S. Korea-Won | |||||||
| 79.1–82.12 | −0.009* (0.004) |
1.025** (0.147) |
−0.039 (0.115) |
0.181 (0.145) |
0.214/2.18 | 47 | 0.027 |
| 83.1–86.12 | −0.003** (0.001) |
0.932** (0.028) |
−0.010 (0.039) |
0.114** (0.038) |
0.810/1.10 | 48 | 0.005 |
| 87.1–90.12 | 0.004** (0.001) |
0.983** (0.040) |
0.129* (0.059) |
−0.113# (0.068) |
0.734/0.80 | 48 | 0.003 |
| 79.1–90.12 | −0.003# (0.001) |
0.945** (0.048) |
0.001 (0.054) |
0.117# (0.063) |
0.344/1.74 | 143 | 0.017 |
| China, P.R.-Yuan | |||||||
| 79.1–82.12 | −0.001 (0.001) | 0.331** (0.042) |
0.110** (0.033) |
0.480** (0.042) |
0.682/1.98 | 47 | 0.008 |
| 83.1–86.12 | −0.011** (0.004) |
0.957** (0.142) |
−0.303## (0.199) | 0.101 (0.196) | 0.673/2.01 | 48 | 0.027 |
| 87.1–90.12 | −0.005 (0.005) | 1.145** (0.164) |
0.485* (0.243) |
−0.685* (0.282) |
0.275/2.17 | 48 | 0.035 |
| 79.1–90.12 | −0.008** (0.002) |
0.813** (0.082) |
0.052 (0.091) | 0.013 (0.107) | 0.056/1.95 | 143 | 0.029 |
| Notes: (a) Standard errors are in parenthesis. (b) All currencies are measured in terms of SDR ($US 0.42, DM 0.19, yen 0.15, French franc 0.12, pound sterling 0.12). (c) **, *, #, and ##, denote statistical significance at the 99%, 95%, 90%, 85% levels, respectively. |
|||||||
| Ex. Rate | Volatility | GNPs | GNP/cap. | Dist. | Adjac. | WH | EC | EFTA | EAEG | APEC R2 | adj. | SEE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1980 | 0.74** (0.02) |
0.29** (0.02) |
−0.56** (0.04) |
0.72** (0.18) |
0.52** (0.15) |
0.23 (0.18) |
0.88** (0.27) |
1.51** (0.17) |
0.71 | 1.20 | ||
| Nominal | −56.11** (7.45) |
0.77** (0.02) |
0.24** (0.02) |
−0.74** (0.05) |
0.24 (0.21) |
0.13 (0.23) |
−0.14 (0.18) |
−0.08 (0.32) |
0.96** (0.36) |
1.31** (0.19) |
0.74 | 1.17 |
| Real | −15.26** (5.25) |
0.74** (0.02) |
0.27** (0.02) |
−0.70** (0.05) |
0.48* (0.22) |
0.17 (0.20) |
−0.09 (0.18) |
−0.22 (0.38) |
0.90* (0.37) |
1.40** (0.22) |
0.76 | 1.14 |
| 1985 | 0.76** (0.02) |
0.25** (0.02) |
−0.70** (0.04) |
0.75** (0.18) |
0.33** (0.16) |
0.44* (0.17) |
0.59* (0.26) |
1.28** (0.17) |
0.74 | 1.17 | ||
| Nominal | 0.23 (0.49) |
0.77** (0.02) |
0.24** (0.02) |
−0.72** (0.04) |
0.61** (0.19) |
0.26## (0.17) |
0.45* (0.18) |
−0.02 (0.31) |
0.79* (0.36) |
1.18** (0.19) |
0.75 | 1.16 |
| Real | 0.09 (0.53) |
0.77** (0.02) |
0.25** (0.02) |
−0.77** (0.05) |
0.46* (0.22) |
−0.05 (0.20) |
0.26## (0.17) |
−0.19 (0.31) |
0.72* (0.36) |
1.13** (0.21) |
0.78 | 1.12 |
| 1990 | 0.75** (0.02) |
0.09** (0.02) |
−0.56** (0.04) |
0.79** (0.16) |
0.92** (0.14) |
0.47** (0.16) |
0.69* (0.24) |
1.36** (0.15) |
0.77 | 1.07 | ||
| Nominal | 5.23** (0.58) |
0.78** (0.02) |
0.09** (0.02) |
−0.66** (0.04) |
0.53** (0.16) |
0.67** (0.14) |
0.41** (0.16) |
−0.03 (0.28) |
0.68* (0.32) |
1.35** (0.17) |
0.80 | 1.02 |
| Real | −8.04# (4.39) |
0.79** (0.02) |
0.12** (0.02) |
−0.61** (0.04) |
0.35# (0.20) |
0.53** (0.17) |
0.29 (0.17) |
−0.09 (0.27) |
0.91** (0.27) |
1.12** (0.17) |
0.83 | 0.97 |
| Notes: (a) The volatility variable is in levels. All the other variables except
the dummies are in logarithms. All the regressions have an intercept for which
the estimate is not reported here. (b) Standard errors are in parenthesis. (c) **, *, # and ## denote statistical significance at the 99%, 95%, 90% and 85% levels, respectively. |
||||||||||||
We also tried estimates of equation (2) that do not impose the constraint that the weights on the major currencies sum to one (and that also exclude the pound sterling).[26] The results are similar: the DM reigns supreme in Europe, the $US in the Western Hemisphere, and the $US – not the yen – is also dominant in East Asia. A ‘t test’ does not reject the constraint that the sum of the three coefficients is 1 for the Western Hemisphere and Asian countries, but often does reject this constraint for the European countries, perhaps reflecting the absence of the pound sterling and French franc.
4.3 An Attempt to Estimate the Effect of Exchange Rate Variability on Trade
One rationale for a country to assign weight to a particular currency in determining its exchange rate is the reasoning that a more stable bilateral exchange rate will help promote bilateral trade with the partner in question. This is a major motivation for exchange rate stabilisation in Europe. There have been quite a few time series studies of the effect of exchange rate uncertainty on trade overall,[27] but fewer cross-section studies of bilateral trade. Three studies with a cross-sectional dimension are Abrams (1980), Brada and Mendez (1988) and De Grauwe (1988). We will re-examine the question here using our data set, which is more recent and more broad, covering 63 countries.
Volatility is defined to be the standard deviation of the first difference of the logarithmic exchange rate. We start with the volatility of nominal exchange rates and embed this term in our gravity equation (1) for 1980, 1985 and 1990. The results are reported in Table 8.[28] Most coefficients are similar to those reported in the earlier results without exchange rate variability (Tables 1 to 3), though the EC and Western Hemisphere bloc dummy variables appear with lower coefficients, suggesting that some of the bloc effect may have been attributable to exchange rate links. In 1980, the coefficient for the volatility term is indeed negative and statistically significant at the 99 per cent level. The magnitude is moderately large.[29] In 1985, the volatility parameter is no longer significant (with the point estimate turning positive), while in 1990, the volatility coefficient is statistically greater than zero.
Theoretical models of the behaviour of the firm often produce the counterintuitive result that, because of convexity in the profit function, exports can be an increasing function of exchange rate variability. Only when the firm is sufficiently risk averse does the intuitive negative effect on trade emerge. Several empirical studies have taken this possibility seriously and perhaps we should also.[30] However, before we take our econometric findings at face value, we should note that a presumably more relevant measure of exchange rate uncertainty is the volatility of the real exchange rate, which takes into account the differential inflation rates in the two countries in addition to movements in the nominal exchange rate.
Regressions including the volatility of real exchange rates are also presented in Table 8. In 1980, the volatility parameter is still negative and statistically significant. The parameter for 1985 is still insignificant. In contrast to the regression with the volatility of nominal rates, the volatility parameter for 1990 is a statistically significant negative number [−8.04].
By way of illustration, these point estimates can be used for some sample calculations. Worldwide, the average level of exchange rate variability in 1990 was 0.376 per cent (Table 5). Our estimates suggest that if this variability was eliminated by adopting fixed exchange rates worldwide, the effect on trade would be 3.02 per cent (=8.04 × 0.376).
These estimated effects cannot be regarded as large. Gagnon (1989) argues on theoretical grounds that the effect of real exchange rate uncertainty on trade volume should be quantitatively small. In a sample calculation, he suggests that an increase in the standard deviation of the exchange rate from 0.05 to 0.08 should reduce the volume of trade undertaken by an individual exporter by 2.5 per cent, which he considers very small.
These results, while less robust than most of the other gravity equation findings, are generally consistent with the hypothesis that real exchange rate volatility depresses bilateral trade. More specifically, they would appear to be evidence that the stabilisation of exchange rates within Europe has helped to promote intra-European trade, and to promote trade within the Pacific, even if the effects are small.
One aspect of the ordinary least squares (OLS) estimates in Table 8 might lead one to think that the role played by exchange rate stabilisation is not small: the estimated trade bloc coefficients seem to fall sharply when the volatility term is included. There is very likely a problem of simultaneous causality. The apparent negative correlation between exchange rate variability and the volume of bilateral trade could easily be due as much to the government's deliberate efforts to stabilise the currency vis-à-vis a valued trading partner, as to the effects of stabilisation on trade. Therefore, we have also tried the method of instrumental variable estimation to tackle the possible simultaneity bias.[31]
We concentrate on the regressions involving the real exchange rates. In 1980, the volatility parameter is still negative and significant at the 95 per cent level. But the magnitude is much smaller than without using the instrument, suggesting that part of the apparent depressing effect of the volatility was indeed due to the simultaneity bias. Strong confirmation comes from an examination of the trade bloc coefficients for the EC and the Western Hemisphere: when the simultaneity is corrected, the presence of the volatility variable no longer reduces the trade bloc coefficient.
In 1990, the volatility parameter again turns into a positive number. The results suggest that if exchange rate volatility did depress bilateral trade, its negative effect appears to have diminished or disappeared over the course of the 1980s. (Tests on data going 15 years further back in history show a negative effect of exchange rate volatility (both nominal and real) on trade that is highly significant in 1965, but that declines steadily in the 1970s.) This sharp change is somewhat surprising. One possible explanation is the rapid development of exchange risk hedging instruments. Our estimates of this effect are, in any case, not sufficiently robust with respect to the functional form, year, or estimation technique to justify strong conclusions. But it seems safe to conclude that the negative effect, if it is still there at all, is very small in magnitude.
5. Conclusions
We have found some evidence of regionalisation of the world economy, into three trading blocs: Europe, the Americas and East Asia. But the patterns of trade, finance and monetary influence are somewhat different from those often supposed.
We have used the gravity model of bilateral trade to evaluate the trade bloc hypothesis, holding constant the sizes of the countries, their GNPs per capita, the distance between them, whether they share a common border and whether they share a common language. We find evidence of a trade bloc on each continent. But the greatest rate of intensification of intra-regional bias has not occurred in East Asia. Rather, in the early 1980s it occurred in the EC, and in the late 1980s in the Western Hemisphere. The strongest apparent effect is not for these three continental groupings, but for APEC.
The lesson that the links across the Pacific are stronger than the links within East Asia is not limited to trade. We performed tests of Japanese versus United States' financial influences on interest rates in 10 Pacific countries. Yen interest rates appear to be gaining influence only in Indonesia, and perhaps Korea. Elsewhere there is no clear trend although, in the English-speaking countries, $US interest rates are the ones gaining influence.
A similar result emerges for currency influences. Although bilateral exchange rates are more stable within East Asia than worldwide, this is not a matter of simply being stable in terms of the most important currency within the region, the yen. While the determination of changes in currency values in Europe is dominated by the DM, and in the Americas is dominated by the $US, changes in currency values in East Asia, with the exception of Singapore and Indonesia, are not much influenced by the yen. Rather the $US is the dominant currency on this side of the Pacific as well as on the other side.
Finally, we found some tentative evidence for a small effect of bilateral exchange rate variability in determining bilateral trade, particularly before the proliferation of hedging instruments in the mid-1980s. But, even if this evidence is thought strong enough to merit being taken seriously, our results do not support the idea that there are strengthening links to the yen in East Asia that have helped to promote intra-regional trade. Rather, if anything, the links to the $US throughout the Pacific have helped to promote Pacific-wide trade and investment.
| Regional Groupings and Main City | |||
|---|---|---|---|
| Americas (WH, 13) | East Asia (EAEG, 10) | ||
| Canada | Ottawa | Japan | Tokyo |
| United States | Chicago | Indonesia | Jakarta |
| Argentina | Buenos Aires | Taiwan | Taipei |
| Brazil | Sao Paulo | Hong Kong | Hong Kong |
| Chile | Santiago | South Korea | Seoul |
| Colombia | Bogota | Malaysia | Kuala Lumpur |
| Ecuador | Quito | Philippines | Manila |
| Mexico | Mexico City | Singapore | Singapore |
| Peru | Lima | Thailand | Bangkok |
| Venezuela | Caracas | China | Shanghai |
| Bolivia | La Paz | Other countries (23) | |
| Paraguay | Asuncion | South Africa | Pretoria |
| Uruguay | Montevideo | Turkey | Ankara |
| European Community (EC, 11) | Yugoslavia | Belgrade | |
| West Germany | Bonn | Israel | Jerusalem |
| France | Paris | Algeria | Algiers |
| Italy | Rome | Libya | Tripoli |
| United Kingdom | London | Nigeria | Lagos |
| Belgium | Brussels | Egypt | Cairo |
| Denmark | Copenhagen | Morocco | Casablanca |
| Netherlands | Amsterdam | Tunisia | Tunis |
| Greece | Athens | Sudan | Khartoum |
| Ireland | Dublin | Ghana | Accra |
| Portugal | Lisbon | Kenya | Nairobi |
| Spain | Madrid | Ethiopia | Addis Ababa |
| European Free Trade Area (EFTA, 6) | Iran | Tehran | |
| Austria | Vienna | Kuwait | Kuwait |
| Finland | Helsinki | Saudi Arabia | Riyadh |
| Norway | Oslo | India | New Delhi |
| Sweden | Stockholm | Pakistan | Karachi |
| Switzerland | Geneva | Hungary | Budapest |
| Iceland | Reykjavik | Poland | Warsaw |
| Australia | Sydney | ||
| New Zealand | Wellington | ||
| Notes: (a) The distance between countries was computed as the great circle
distance – between the relevant pair of cities (b) APEC consists of East Asia, plus Australia, New Zealand, Canada and the United States. |
|||
Footnotes
The authors thank Benjamin Chui, Xiong Bai Fan and Menzie Chinn for research assistance, Tamim Bayoumi, Richard Portes, and Joe Gagnon for comments on an earlier draft and the discussants Ross Garnaut and Zenta Nakajima and other conference participants for comments. Thanks also go to Warwick McKibbin for help in obtaining data, and the Centre for International and Development Economics Research (funded at the University of California, Berkeley by the Ford Foundation) and the Japan-United States Friendship Commission (a US Government agency) for research support. Some of the work was carried out while Frankel was a Visiting Scholar at the Research Department of the International Monetary Fund and Wei was a Visiting Scholar at the Centre for Pacific Basin Monetary and Economic Studies at the Federal Reserve Bank of San Francisco. However, the views expressed are not those of any institution. [*]
Somewhat smaller increases took place in the intra-regional trade shares of the Americas and Europe, respectively. The greatest increase, from 42 per cent to 53 per cent, took place among the APEC countries. [1]
Two others are Wang and Winters (1991) and Hamilton and Winters (1992). The focus of these papers is on potential Eastern European trade patterns; but they report statistically significant within-region biases to the following groupings: EC, Latin America, ASEAN, former British colonies, Generalised System of Preferences (GSP), and EC preferences under the Lomé convention. The most classic reference is Linnemann (1966). [2]
An easy way to hold size constant is to scale bilateral trade by GNPs or total trade. Such calculations are sometimes called ‘trade intensities’. See Anderson and Norheim (1992) and Drysdale and Garnaut (1992). Our main conclusions are for the most part consistent with theirs. [3]
The list of countries and regional groupings is given in the Appendix. [4]
The specification implies that trade between two equal-sized countries (say, of size 0.5) will be greater than trade between a large and small country (say, of size 0.9 and 0.1). This property of models with imperfect competition is not a property of the classical Heckscher-Ohlin theory of comparative advantage; see Helpman (1987) and Helpman and Krugman (1985, Section 1.5). Rudimentary foundations for the gravity model are found in Linneman (1966) and also in other papers surveyed by Deardorff (1984, pp. 503–506) and Wang and Winters (1991). [5]
When distance, distance squared and the log of distance are included at the same time, only the last is significant. [6]
Linnemann (1966) obtains similar estimates for this parameter (in the range 0.21 to 0.27) and for other parameters, for the year 1959. [7]
See, for example, Rose (1991). [8]
However, the use of the multiplicative form itself changes the results somewhat. These results are reported in an Appendix Table A2–A3 in Frankel and Wei (1993). Linnemann (1966) and Wang and Winters (1992) address the problem of trade flows so small as to be recorded as zero in another way: by trying the tests substituting fractions (like 0.5) of the minimum recordable unit for the zeros. They too found that inclusion of the missing values made little substantive difference to the results. [9]
These results are not reported here but are described in Frankel (1992). [10]
This greater openness indicates that trade diversion is not taking place in East Asia. The openness effect is also significant for the EC where it eliminates the significance of the bloc effect in some years. These results are reported in Frankel, Stein and Wei (1993). [11]
See Frankel, Stein and Wei (1993). [12]
This corresponds to findings in Petri (1993), based on somewhat simpler calculations. [13]
See Frankel and Wei (1993). [14]
See Frankel, Stein and Wei (1993). NAFTA had not experienced any significant bloc effect as of 1990. [15]
The coefficient for English is never close to statistically significant, beyond the general coefficient for common languages. [16]
Another way to approach the question of whether East Asia is becoming a financial bloc would be to look at saving-investment correlations. Bayoumi and Sterne (1992) find that saving-investment correlations are lower among East Asian countries (as within other regions) than worldwide, suggesting an extra degree of intra-regional capital mobility by this test. [17]
The major exception is Hong Kong, which is pegged to the $US, and has open financial markets. [18]
Table 4 reports results where the foreign interest rates are the Eurodollar and Euroyen rates, taken from the London markets. Table 10a in Chinn and Frankel (1993) reports analogous regressions where the foreign interest rates are taken from the New York and Tokyo financial markets respectively. The results are similar. [19]
Multicollinearity does not, of course, bias the coefficient estimates or their reported standard errors. It just makes it unlikely that there will be enough information in the data to answer the question at hand. [20]
The results are reported in Table 12 of Chinn and Frankel (1993). [21]
The results are reported in Table 13 of Chinn and Frankel (1993). [22]
Why do countries keep the weights secret? It allows the governments to devalue their currencies secretly when they so desire. But secret weights undermine the governments' ability to commit credibly to a low inflationary monetary policy (Lowell 1992). [23]
See Frankel and Wei (1992) and Frankel (1993), respectively. [24]
The results for the EC and EFTA countries are reported in Tables 5 and 6, respectively, of Frankel and Wei (1993). [25]
These tables are reported in Frankel and Wei (1993). [26]
For example, Hooper and Kohlhagen (1978), Kenen and Rodrik (1986), Akhtar and Hilton (1984) and Cushman (1986). The literature is surveyed in Edison and Melvin (1990). [27]
These results extend those in Table 13a of Frankel and Wei (1992) by measuring volatility as the level of the standard deviation rather than its log, thus allowing the experiment of asking how much trade would increase if exchange rate variabilities, like those reported in Table 5, were reduced to zero. These results also add the EFTA bloc variable. [28]
The estimate in Frankel and Wei (1992) suggests that, on average, a doubling of the standard deviation reduces bilateral trade by an apparent 4.6 per cent (= 0.066 ln (2)), holding constant all other variables. [29]
See for example, Caballero and Corbo (1989). Empirically, however, they find a negative relationship. [30]
The standard deviation of relative money supply is our instrument for the volatility of exchange rates. The results are reported in Table 10 of Frankel and Wei (1993). [31]
References
Abrams, R. (1980), ‘International Trade Flows Under Flexible Exchange Rates’, Economic Review, Federal Reserve Bank of Kansas City, March, pp. 3–10.
Akhtar, M.A. and S. Hilton (1984), ‘Effects of Exchange Rate Uncertainty on German and U.S. Trade’, Federal Reserve Bank of New York Quarterly Review, 9(1), Spring, pp. 7–16.
Anderson, K. and H. Norheim (1992), ‘History, Geography and Regional Economic Integration’, GATT Secretariat Conference, Geneva, Oct.; forthcoming in K. Anderson and R. Blackhurst (eds), Regionalism and the Global Trading System, Harvester Wheatsheaf, London.
Bayoumi, T. and G. Sterne (1992), ‘Regional Trading Blocs, Mobile Capital and Exchange Rate Co-ordination’, International Monetary Fund, August 1992; Bank of England Discussion Paper, 1993.
Brada, J. and J. Mendez (1988), ‘Exchange Rate Risk, Exchange Rate Regimes and the Level of International Trade’, Kyklos, 41(2), pp. 263–280.
Caballero, R. and V. Corbo (1989), ‘The Effect of Real Exchange Rate Uncertainty on Exports: Empirical Evidence’, The World Bank Economic Review, 3(2), May, pp. 263–278.
Chinn, M. and J. Frankel (1993), ‘Financial Links Around the Pacific Rim: 1982–1992’, forthcoming in R. Glick and M. Hutchison (eds), Exchange Rate Policy and Interdependence: Perspectives from the Pacific Basin, Cambridge University Press.
Cushman, D. (1986), ‘Has Exchange Risk Depressed International Trade? The Impact of Third-Country Exchange Risk’, Journal of International Money and Finance, 5, September, pp. 361–379.
Deardorff, A. (1984), ‘Testing Trade Theories and Predicting Trade Flows’, in R. Jones and P. Kenen (eds), Handbook of International Economics, Vol. 1, Elsevier Science Publishers, Amsterdam, pp. 467–517.
de Grauwe, P. (1988), ‘Exchange Rate Variability and the Slowdown in Growth of International Trade’, IMF Staff Papers, 35, pp. 63–84.
Drysdale, P. and R. Garnaut (1992), The Pacific: An Application of a General Theory of Economic Integration, paper presented at the Twentieth Pacific Trade and Development Conference, Washington, D.C., September 10–12.
Edison, H. and M. Melvin (1990), ‘The Determinants and Implications of the Choice of an Exchange Rate System’, in W. Haraf and T. Willett (eds), Monetary Policy for a Volatile Global Economy, AEI Press, Washington, D.C.
Frankel, J.A. (1993), ‘Is Japan Creating a Yen Bloc in East Asia and the Pacific?’, NBER Working Paper No. 4050; in J. Frankel and M. Kahler (eds), Regionalism and Rivalry: Japan and the U.S. in Pacific Asia, University of Chicago Press, Chicago.
Frankel, J.A., E. Stein and S. Wei (1993), Trading Blocs: The Natural, the Unnatural, and the Super-Natural, paper presented to the NBER Sixth Inter-American Seminar in Economics, Caracas, Venezuela, May 29; forthcoming in Journal of Development Economics.
Frankel, J.A. and S. Wei (1992), Yen Bloc or Dollar Bloc: Exchange Rate Policies of the East Asian Economies, paper presented to the Third Annual NBER East Asia Seminar on Economics, Sapporo, Japan, June 17–19, 1992; forthcoming in T. Ito and A. Krueger (eds), University of Chicago Press, 1994.
Frankel, J.A. and S. Wei (1993), ‘Trade Blocs and Currency Blocs’, NBER Working Paper No. 4335, April.
Gagnon, J. (1989), ‘Exchange Rate Variability and the Level of International Trade’, International Finance Discussion Papers No. 369, Federal Reserve Board, December.
Glick, R. (1987), ‘Interest Rate Linkages in the Pacific Basin’, San Francisco Federal Reserve Board Economic Review, 3, Summer, pp. 31–42.
Glick, R. and M. Hutchison (1990), ‘Financial Liberalisation in the Pacific Basin: Implications for Real Interest Rate Linkages’, Journal of the Japanese and International Economies, 4, pp. 36–48.
Hamilton, C. and L.A. Winters (1992), ‘Opening Up International Trade in Eastern Europe’, Economic Policy, April, pp. 78–116.
Helpman, E. (1987), ‘Imperfect Competition and International Trade: Evidence from Fourteen Industrial Countries’, Journal of the Japanese and International Economies, 1, pp. 62–81.
Helpman, E. and P. Krugman (1985), Market Structure and Foreign Trade, MIT Press, Cambridge.
Hooper, P. and S. Kohlhagen (1978), ‘The Effect of Exchange Rate Uncertainty on the Prices and Volume of International Trade’, Journal of International Economics, 8, November, pp. 483–511.
Kenen, P. and D. Rodrik (1986), ‘Measuring and Analyzing the Effects of Short-term Volatility in Real Exchange Rates’, Review of Economics and Statistics, 68(2), pp. 311–315.
Krugman, P.R. (1991), ‘The Move Toward Free Trade Zones’, in Policy Implications of Trade and Currency Zones, a symposium sponsored by the Federal Reserve Bank of Kansas City, Jackson Hole, August, pp. 7–42.
Linneman, H. (1966), An Econometric Study of International Trade Flows, North-Holland, Amsterdam.
Lowell, J. (1992), Do Governments Do What They Say (And Do We Believe Them): Two Essays on National Debt and Exchange Regime Policies, PhD thesis, Department of Economics, University of California, Berkeley.
Petri, P. (1993), ‘The East Asian Trading Bloc: An Analytical History’ in J.A. Frankel and M. Kahler (eds), Regionalism and Rivalry: Japan and the U.S. in Pacific Asia, University of Chicago Press, Chicago.
Rose, A. (1991), ‘Why Has Trade Grown Faster than Income?’, Canadian Journal of Economics, 24(2), pp. 417–427.
Saxonhouse, G. (1989), ‘Differentiated Products, Economies of Scale and Access to the Japanese Market’, in R. Feenstra (ed.), Trade Policies for International Competitiveness, University of Chicago Press, Chicago, pp. 145–174.
Wang, Z.K. and L.A. Winters (1991), ‘The Trading Potential of Eastern Europe’, Centre for Economic Policy Research Discussion Paper No. 610, November.