Bulletin – September 2010 Interpreting Market Responses to Economic Data
- Download the article 232KB
Abstract
This article discusses how bond, equity and foreign exchange markets have responded to the surprise component of Australian and US macroeconomic data announcements over the past decade. The bond and equity market responses are used to infer changes in market expectations for interest rates and dividend growth rates. Both interest rates and expected dividend growth rates are shown to increase by a similar magnitude in response to upside inflation and employment surprises. The estimated changes in the interest rate and expected dividend growth rate differentials between Australia and the US are also compared with the exchange rate response to data surprises. This allows an assessment of the relationship between expected economic fundamentals and the exchange rate.
Introduction
This article examines the response of financial market prices to the surprise component of macroeconomic data announcements in Australia and the United States. In particular, it uses data on bond yields and equity prices to examine the effect of data surprises on expectations for interest rates and dividend growth. The results suggest that announcements that cause interest rates to increase (decrease) also tend to cause a similarly sized increase (decrease) in the expected rate of growth in dividends. In addition, they suggest that US data announcements have a significant effect on Australian financial markets.
The article first presents estimates of the response of the US and Australian bond, equity and foreign exchange markets to macroeconomic data surprises. It then uses the relationship between bond yields, equity prices and future dividends to examine how announcements affect expectations regarding dividend growth.[1] It concludes by examining the extent to which the implied changes in expectations of dividends and interest rates in response to data announcements in the United States and Australia are consistent with the response of the AUD/USD exchange rate.
Asset Price Responses to Data Surprises
Estimating the average response of asset prices to data announcements requires a measure of the ‘surprise’ component of the announcements as expected data outcomes will already be incorporated in market pricing. Here the surprise component of each data announcement is calculated as the difference between the actual outcome and the median market forecast published on Bloomberg, plus any revision to the previous period's outcome. In order to allow comparisons across data releases, this surprise component (Sk,t) is standardised using the historical standard deviation of surprises for each release (σ(Sk,t)). The surprise index for data series k is given as:

This article examines the response of Australian and US markets to employment and CPI inflation announcements for both countries. The results are representative of those for a larger set of data announcements including: GDP, retail sales, housing and producer price data.
The asset price response to the data surprise (Rn,t) is calculated as the percentage change in price between the trade immediately prior to the announcement and the first trade five minutes after the announcement. Using a narrow five-minute window around the data announcement minimises the possibility that news other than the data surprise is contaminating the asset price response. Prices for bonds and equities are measured using futures rather than the underlying asset or index because futures markets are typically open even when the underlying physical markets are closed, allowing cross-country responses to be estimated.[2] For bond yields, the futures prices for the 10-year US Treasury bond (UST) and the 10-year Commonwealth Government Security (CGS) are used, while futures for the US S&P 500 equity index and the Australian ASX 200 equity index are used for equity markets.
The calculated data surprise and price response series are used to estimate the following relationship for each asset class:
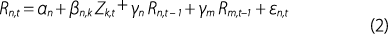
In this regression, the estimated βn,k is the average percentage change in the price of asset n in response to a one-standard deviation surprise in data series k. (The coefficient on the autoregressive term, γn, captures the background momentum in returns of the asset n, and the γm coefficients (m≠n) capture any cross-market effects from the other two asset markets). The regression is estimated using ordinary least squares (OLS).[3] A positive estimate of βn,k indicates a positive asset price response to data surprises on average over the sample.
Table 1 presents the estimated average responses to inflation and employment surprises for the bond, equity and foreign exchange markets in Australia and the United States.[4] Although there are differences in the magnitude of the responses across the two countries, the results indicate that bond yields typically rise in response to positive inflation and employment surprises, with the responses a little stronger for the latter. Equity market returns are typically negative (that is, equity prices fall) in response to positive inflation surprises, but rise in response to positive employment surprises. Positive inflation and employment surprises cause the local currency to appreciate relative to the other country's currency.
| Data release | Asset market response | |||
|---|---|---|---|---|
| Exchange rate per cent |
Equity prices per cent |
Bond prices per cent |
Bond yields percentage points |
|
| AUD/USD | S&P 500 | 10-year UST | 10-year UST | |
| US CPI | −0.05** | −0.13** | −0.08** | 0.01** |
| Australian CPI | 0.08** | 0.00** | −0.01** | 0.00** |
| ASX 200 | 10-year CGS | 10-year CGS | ||
| US CPI | −0.08** | −0.09** | 0.01** | |
| Australian CPI | −0.12** | −0.18** | 0.02** | |
| AUD/USD | S&P 500 | 10-year UST | 10-year UST | |
| US employment | −0.12** | 0.26** | −0.26** | 0.04** |
| Australian employment | 0.22** | 0.01** | −0.01** | 0.00** |
| ASX 200 | 10-year CGS | 10-year CGS | ||
| US employment | 0.13** | −0.28** | 0.04** | |
| Australian employment | 0.02** | −0.17** | 0.02** | |
|
Note: **, * indicate significance at the 1 and 5 per cent levels respectively Sources: Bloomberg; RBA; SIRCA |
||||
The magnitudes of these estimates are broadly in line with those found in the literature. The absolute sizes of the responses are in the order of 25 to 65 per cent of the average daily movement in prices for each market. Relative to typical daily volatility, the bond markets are more sensitive to data surprises than are the equity and foreign exchange markets.
There are considerable differences between the responsiveness of markets to different types of releases in the two countries. For the United States, the largest responses across all markets are for employment surprises, but Australian markets (with the exception of the foreign exchange market) tend to react more to inflation news. This may partly reflect the fact that CPI data in Australia are quarterly rather than monthly, and so surprises are viewed by market participants as containing more significant information than US inflation announcements.
Although the direction of the cross-country price responses are consistent with the own-country responses, as expected the largest cross-country effects are for Australian markets responding to US announcements. In particular, US data surprises induce Australian bond yields to adjust by around the same magnitude as US bond yields, while the response in Australian equity prices is about half the US market's response. In contrast, Australian data surprises generate only very small responses in US markets – that they are statistically significant likely reflects the timing of Australian announcements, which occur at a time of day when there is generally very little other news affecting US markets. Although these cross-country responses are broadly as expected, it is interesting that the Australian equity market is more responsive to US inflation and employment news than to Australian employment news. This suggests that in smaller markets like Australia, the ‘lead’ from the major market is at least as significant for pricing assets as is news about local economic fundamentals.
Inferring the Response of Dividend Growth Rate Expectations
The standard dividend growth model of equity prices can be used together with the bond and equity market responses discussed above to calculate the average change in the expected dividend growth rate in response to data surprises. Intuitively, if equity prices are related to dividend growth expectations and expected interest rates (the discount factor), then it should be possible to use the observed change in equity prices and interest rates to calculate the implied change in the market's dividend growth rate expectations.
The equity price model can be used to relate changes in equity prices to changes in expected dividend growth, the discount factor and excess return (or equity risk premium) as outlined in Appendix A. Assuming that the risk premium is fixed in the narrow window around the data releases, the model allows an estimate of the change in the market's expected dividend growth rate (Δg) to be ‘backed-out’ from the observed changes in bond yields (Δi) and the proportional change in equity prices (ΔΕ/Ε):
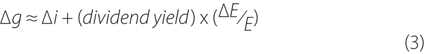
For the Australian and US data announcements, the inferred changes in the expected dividend growth rates are invariably of the same sign, and of a similar magnitude, to the interest rate responses (Table 2). An examination of Equation (3) indicates that this is not a surprising result. The final term in the equation is proportional to the average dividend yield, which is typically a small fraction. Unless the response of equity prices is very large, the change in the expected dividend growth rate will be similar to the change in the interest rate.[5]
| US markets | Australian markets | |||
|---|---|---|---|---|
| US data release | ||||
| ΔiUS | ΔgUS | ΔiAU | ΔgAU | |
| CPI | 0.01 | 0.01 | 0.01 | 0.01 |
| Employment | 0.04 | 0.05 | 0.04 | 0.04 |
| Australian data release | ||||
| ΔiUS | ΔgUS | ΔiAU | ΔgAU | |
| CPI | 0.00 | 0.00 | 0.02 | 0.02 |
| Employment | 0.00 | 0.00 | 0.02 | 0.02 |
|
Sources: Bloomberg; RBA; SIRCA |
||||
One implication of these results is that although equity prices tend to respond negatively to positive inflation surprises and positively to employment surprises, this does not imply negative revisions to dividend growth expectations in response to inflation surprises. Rather, the small fall in equity prices in response to positive inflation surprises is due to the interest rate increase, which is almost, but not entirely, offset by the increase in the expected dividend growth rate. In the case of US employment surprises, the positive equity price response on average is just large enough to imply an expected dividend growth rate response (Δg) slightly larger than the increase in the interest rate (Δi).
One matter that needs to be addressed in interpreting these results is the extent to which the change in nominal interest rates reflects a change in real interest rates. The nominal interest rate responses could be driven by a change in real interest rates and/or inflation expectations – this latter possibility is perhaps most important for inflation surprises, which could influence the inflation premium in nominal yields.[6] However, a comparison of the response of nominal and inflation-linked bond yields to data announcements suggests that the changes in nominal yields are largely, though not entirely, due to changes in real yields, with only a small variation in the inflation component of nominal yields. The fact that equity prices fall in response to positive inflation surprises is also an indication that there is an increase in real interest rates and that the results cannot be due entirely to higher inflation expectations. Higher inflation would see nominal equity prices increase not decrease. Therefore, while the time series of high-frequency price data on index-linked bonds is not long enough to definitively separate the shift in nominal yields into real and inflation compensation components for the whole sample, it appears that the estimates of Δi and Δg provide an approximate (although slightly upwardly biased) estimate of the change in the market's expectations of real interest rates and the expected real rate of dividend growth.
Another caveat relates to the validity of the assumption that the equity risk premium is fixed around data announcements. It is possible that the estimated changes in the expected dividend growth rates are actually due to shifts in the equity risk premium in response to the data announcement news (according to the equity price model a fall in the risk premium, for example, would have a positive effect on equity prices). There is some evidence in the literature, from Bernanke and Kuttner's (2005) structural model estimates, that the risk premium changes in response to monetary policy surprises; however, that study does not specifically investigate the effect that macroeconomic data announcements (as opposed to policy announcements) have on the risk premium. In theory, the equity risk premium will reflect investors' preferences for risk and the expected volatility of equity prices. It is difficult to assess empirically the impact of data announcements on investor preferences for risk, but it is possible to examine the impact of announcements on expected volatility of equity prices using implied volatilities from options markets.[7] Estimated coefficients from regressions of the VIX measure of implied volatility for the S&P500 on the data surprise indices are not significant, suggesting that the assumption of a fixed risk premium is valid.[8]
Cross-country Differentials and the Exchange Rate Response
The above discussion presented estimates of how interest rates and expected dividend growth rates – two key drivers of expected returns on financial assets – change in response to data announcements. These key drivers of expected returns should also influence the relative attractiveness of Australian and US dollar assets, and therefore the exchange rate. This section compares the exchange rate response around data announcements with the change in the interest rate and dividend growth rate differentials between the two countries. The comparison can be viewed as a check on whether the foreign exchange market's response to data announcements is consistent with the implied change in interest rates and expected dividend growth rates observed in the bond and equity markets. Underlying this exercise is a simple framework in which the spot AUD/USD exchange rate (SAUD/USD)is a positive function of the interest rate and expected dividend growth rate differentials between Australia and the United States:
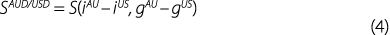
The estimated changes in the interest rate and expected growth rate differentials in response to US data surprises are close to zero, which is a consequence of the Australian markets following the lead of US markets when US data are released (Table 3). Despite this, there is still on average a significant depreciation of the AUD/USD exchange rate in response to positive US data surprises. In contrast, Australian data surprises do induce positive changes in the interest rate and growth rate differentials as well as an appreciation of the AUD/USD exchange rate. This positive relationship between the interest rate differential and the exchange rate is consistent with other time series modelling of the exchange rate. However, the relative sizes of the responses are not consistent with a simple positive relationship between the interest rate differential and the exchange rate. For example, despite the change in the interest rate differential being larger for inflation surprises, the appreciation of the Australian dollar is significantly larger in response to Australian employment surprises. Overall, these results suggest that changes in interest rate and growth rate differentials are insufficient to explain the responsiveness of the foreign exchange market to data announcements. This finding resonates with the vast literature on exchange rate modelling, which generally concludes that economic fundamentals do not fully explain short-run movements in nominal exchange rates.
| Δ AUD/USD | Δ (iAU–iUS) | Δ (gAU–gUS) | |
|---|---|---|---|
| US data release | |||
| CPI | −0.05 | 0.00 | 0.00 |
| Employment | −0.12 | −0.01 | 0.00 |
| Australian data release | |||
| CPI | 0.08 | 0.03 | 0.02 |
| Employment | 0.22 | 0.02 | 0.02 |
|
Sources: Bloomberg; RBA; SIRCA |
|||
Summary and Assessment
The results in this articles show that nominal interest rate and dividend growth rate expectations react in a similar manner to a given data surprise. Data announcements that cause bond yields to increase also cause the expected dividend growth rate to increase. Therefore, the negative response of equity prices to positive inflation data surprises is best interpreted as reflecting a slightly larger impact from the increase in interest rate expectations compared with the increase in dividend growth expectations, rather than the being due to a fall in the expected growth rate of dividends.
Looking at the cross-country responses to data surprises, US data surprises have a significant effect on Australian interest rate and dividend growth expectations, in some cases larger than the impact from the equivalent Australian release. As a result, the changes in expected interest rate and dividend growth rate differentials following a US data surprise are typically very small. Nevertheless, the average response of the AUD/USD exchange rate is found to be significant. This result, along with the irregular relationship between the exchange rate and the interest and dividend differentials in response to Australian data, is consistent with other research. It suggests there is little evidence that short-term movements in nominal exchange rates are well explained by changes in expected economic fundamentals.
Appendix A: Equity Price Decomposition
The classic Gordon (1962) dividend growth model of equity prices states that equity prices, are the sum of risk-adjusted discounted future dividends:

where i is the nominal interest rate, g is the expected growth rate of dividends (D) and ρ is the expected excess return for holding risky equities (equity risk premium).[9]
Using standard calculus, Equation (A1) can be used to decompose changes in equity prices into component changes in future the dividend growth rate, the interest rate and the equity risk premium:.
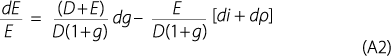
where the left-hand side represents the percentage change in equity prices in response to a data surprise. In line with standard intuition, equity prices are positively related to expected dividend growth and negatively related to expected interest rates and the equity risk premium.
As in Boyd et al (2005), the risk premium is assumed to be fixed
around the time of the data announcements. Thus, rearranging Equation (A2)
and allowing for discrete changes in g and i gives an approximate
expression for the change in dividend growth expectations (Δg)
in terms of the equity price response and the change in the interest rate
(Δi)[10]:

Footnotes
The authors completed this work in International Department. [*]
Campbell and Lewis (1998) show that Australian bond yields react significantly to US data surprises, and Kim and In (2002) show that Australian equity markets react significantly to US data surprises. There are many studies for the United States, including Anderson et al (2007) and Boyd, Hu and Jagannathan (2005) that apply similar approaches to measuring the response of financial prices to news, but these papers do not typically interpret the results within a single framework that includes both expected interest rates and dividend growth rates. [1]
High-frequency price data are sourced from the Reuters RDTH database provided by the Securities Industry Research Centre of Asia-Pacific (SIRCA). Returns are calculated using the closest-to-maturity contract to minimise the difference between changes in the spot and futures prices. A comparison of the reactions of ASX spot prices for equities and futures prices to Australian data surprises indicated that the coefficient estimates are not sensitive to the choice of price data. [2]
Robust standard errors are calculated to deal with any residual heteroscedasticity in the error term (εn,t). As is often the case for financial market returns, the coefficients on the autoregressive terms are generally found to be significant. However, the coefficients on the lagged returns for the other asset classes (when m≠n) are generally not significant. [3]
The bond yield responses are calculated from the bond price responses by making an adjustment for the average duration of the underlying bond. [4]
The estimated average dividend yield is 1.9 per cent for the US and 4.1 per cent for Australia over the sample period. [5]
The correlation between the change in nominal yields and real yields is 0.8 for a sample of US data surprises between April 2009 and February 2010. Using a larger sample, Beechey and Wright (2009) also find that most of the sensitivity in nominal yields can be attributed to changes in real yields in response to real data releases, but that expected inflation compensation is sensitive to nominal data surprises. [6]
Arguably it is reasonable to assume that investors' risk preferences should not change in response to small surprises in economic data announcements. [7]
The VIX measure of implied volatility is calculated in real time by the Chicago Board Options Exchange and measures the implied volatility from options prices on the S&P 500 index. [8]
In the original model the variables are constant, but Jagannathan, McGratten and Scherbina (2000) show that the model still holds when the variables change over time. In that case, parameters in the pricing equation are interpreted as the weighted averages of their expected future values. [9]
Equation (A3) is an approximation based on the fact that (D+E)/E≈1, D/(D+E)≈D/E and 1+g≈1. [10]
References
Anderson TG, T Bollerslev, X Diebold and C Vega (2007), ‘Real-time Price Discovery in Global Stock, Bond and Foreign Exchange Markets’, Journal of International Economics, 73, pp 251–277.
Beechey MJ and JH Wright (2009), ‘The High-frequency Impact of News on Long-Term Yields and Forward Rates: Is it Real?’, Journal of Monetary Economics, 56, pp 535–544.
Bernanke BS and K Kuttner (2005), ‘What Explains the Stock Market's Reaction to Federal Reserve Policy?’, Journal of Finance, 60(3), pp 1221–1257.
Boyd JH, J Hu and R Jagannathan (2005), ‘The Stock Market's Reaction to Unemployment News: Why Bad News is Usually Good for Stocks’, Journal of Finance, 60(2), pp 649–672.
Campbell F and E Lewis (1998), ‘What Moves Yields in Australia?’, RBA Research Discussion Paper No 9808. Available at <http://www.rba.gov.au/publications/rdp/1998/9808.html>.
Gordon MJ (1962), The Investment, Financing, and Valuation of the Corporation, Irwin, Homewood.
Jagannathan R, ER McGratten and A Scherbina (2000), ‘The Declining US Equity Premium’, Federal Reserve Bank of Minneapolis, Quarterly Review, 24, pp 3–19.
Kim S and F In (2002), ‘The Influence of Foreign Stock Markets and Macroeconomic News Announcements on Australian Financial Markets’, Pacific-Basin Finance Journal, 10, pp 571–582.