Research Discussion Paper – RDP 2021-02 Star Wars at Central Banks
1. Introduction
How credible is central bank research? The answer matters for the policymakers who use the research and for the taxpayers who fund it.
We investigate an aspect of credibility by searching for evidence of researcher bias, which is a tendency to use undisclosed analytical procedures that raise measured levels of statistical significance (stars) in artificial ways. For example, a researcher might try several defensible methods for cleaning a dataset and favour those that yield the most statistically significant research results. In doing so, the researcher exaggerates the strength of evidence against their null hypothesis, potentially via inflated economic significance. The bias need not be malicious or even conscious.
Earlier research has investigated researcher bias in economics, but has focused mainly on journal publications. Christensen and Miguel (2018) survey the findings, which suggest the bias is common, and partly the result of journal publication incentives. More recent work by Blanco-Perez and Brodeur (2020) and Brodeur, Cook and Heyes (2020) corroborates these ideas. The literature uses several bias-detection methods. For our paper, we use the p-curve, from Simonsohn, Nelson and Simmons (2014), as well as the z-curve, from Brodeur et al (2016).[1] We choose these methods because they suit investigations into large bodies of research that cover a mix of different topics. But the methods also have shortcomings: the p-curve generates a high rate of false negatives and the z-curve requires strong assumptions.
Applying these methods to central bank research is a useful contribution to the literature because the existing findings about journals need not generalise. On the one hand, formal incentives for central bankers to publish in journals are often weak; much of their long-form research remains in the form of discussion papers. On the other hand, some central bank research does appear in journals, and there might be other relevant incentive problems to worry about, such as pressures to support house views (see Allen, Bean and De Gregorio (2016) and Haldane (2018)). Depending on how central bankers choose research topics, pressures to support house views could plausibly encourage findings of statistical significance.
To our knowledge, investigating researcher bias at central banks has been the topic of just one other empirical paper, by Fabo et al (2020). Focusing solely on research about the effects of quantitative easing, they find that central banks tend to estimate more significant positive effects than other researchers do. This is a worrisome finding because central bankers are accountable for the effects of quantitative easing, and positive effects of quantitative easing are likely to form part of the house view. Our work complements Fabo et al (2020) as our methods free us from having to benchmark against research from outside of central banks, benchmarks that the survey by Christensen and Miguel (2018) suggests would be biased. Our methods also allow us to study a wider body of central bank research at once. To conduct our search, we compile a dataset on 2 decades of discussion papers from the Federal Reserve Bank of Minneapolis (the Minneapolis Fed), the Reserve Bank of Australia (RBA) and the Reserve Bank of New Zealand (RBNZ). Where possible, we include parallel analysis of top economic journals, using the dataset from Brodeur et al (2016).
Another of our contributions to the literature is to conduct a new investigation into the merits of the z-curve assumptions. We test the assumptions using a placebo exercise, looking for researcher bias in hypothesis tests about control variables. We also investigate problems that we think could arise from applying the z-curve to research containing transparent use of data-driven model selection techniques.
Our headline findings are mixed:
- Using the p-curve method, we find that none of our central bank subsamples produce evidence of researcher bias.
- Using the z-curve method, we find that almost all of our central bank subsamples produce evidence of researcher bias.
- However, our placebo exercise and investigations into data-driven model selection cast doubt on the z-curve method.
A related finding – but one we are unable to explain – is that central banks produce results with patterns different from those in top journals, there being less bunching around the 5 per cent significance threshold of |z| = 1.96 (Figure 1). We offer some speculative explanations for the difference, but ultimately leave it as a puzzle for future work.
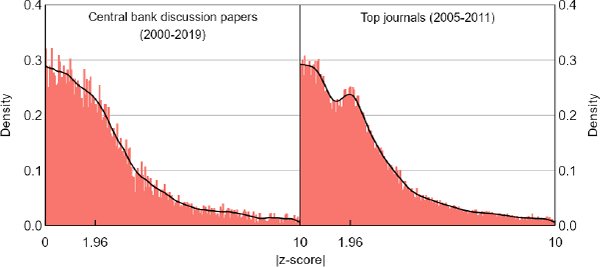
Notes: We plot the absolute values of de-rounded t-statistics (very close to z-score equivalents) for results that are discussed in the main text of a paper. We use the term ‘Top journals’ as loose shorthand for The American Economic Review, the Journal of Political Economy, and The Quarterly Journal of Economics.
Sources: Authors' calculations; Brodeur et al (2016); Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
2. Researcher Bias is about Undisclosed Exaggeration
Our use of the term researcher bias is based on an influential paper in the medical sciences, by Ioannidis (2005), who defines it as ‘the combination of various design, data, analysis, and presentation factors that tend to produce research findings when they should not be produced’. It is not to be confused with ‘chance variability that causes some findings to be false by chance even though the study design, data, analysis, and presentation are perfect’ (p 0697).
We use a modified definition, mainly to clarify the most important aspects of what we understand Ioannidis to mean. The main change is to elaborate on ‘should’, to reflect our view that however much a procedure distorts findings, disclosing it exonerates the researcher from bias. In other words, it is non-disclosure, intentional or not, that makes the distortion of results most problematic and worthy of investigation. Hence our definition focuses on undisclosed procedures.
Other research on this topic, including Simonsohn et al (2014) and Brodeur et al (2016), uses different language. For example, Brodeur et al (2016) use the term inflation and define it as a residual from a technical decomposition (the z-curve method). Brodeur et al (2020) use the more loaded term p-hacking. The intentions behind these other terms and definitions, as we understand them, are the same as ours.
3. Our Bias-detection Methods Have Important Strengths and Weaknesses
3.1 Bayes' rule provides a helpful unifying framework
The p-curve and z-curve methods fit into a class of bias-detection methods that look for telling patterns in the distribution of observed test statistics. Other methods often involve replicating research, as in Simonsohn, Simmons and Nelson (2020). The pattern recognition methods appeal to us because they use fewer resources, which is important when investigating large bodies of work. But compromises are needed to overcome some conceptual challenges. Simonsohn et al (2014) and Brodeur et al (2016) detail the p-curve and z-curve methods, and we do not repeat that technical material here. Instead, we explain the shared intuition underlying these methods, using a framework we have built around Bayes' rule.
Both methods aim to detect researcher bias in the probability distribution of test statistics that are the primary interest of research projects. Call these probabilities P[z], where z is the z-score equivalent of each test statistic of primary interest. (Although z-scores are continuous variables, we use discrete variable notation to simplify the discussion.) The central challenge is that we observe only z-scores that researchers disseminate. That is, we draw z-scores with probability P[z|disseminated]. Following Bayes' rule, this distribution is a distorted version of the P[z] distribution, whereby
The distorting term, P[disseminated|z], captures the fact that researchers are more likely to disseminate papers containing statistically significant test statistics (Franco, Malhotra and Simonovits 2014). It is not our objective to study this dissemination bias, but we do need to account for it.[2]
A graphical example helps to explain further. Suppose the z-scores in our sample suggest a distribution for P[z|disseminated] as shown on the left of Figure 2. On first impression, the peak after the 5 per cent significance threshold of |z| = 1.96 might look like researcher bias, since nature is unlikely to produce such patterns at arbitrary, human-made thresholds. But if we entertain a form of dissemination bias as shown in the middle, according to Bayes' rule we must also entertain a single-peaked distribution for P[z] as shown on the right. In an informal sense at least, that P[z] distribution does not contain any obvious anomalies that might be signs of researcher bias.
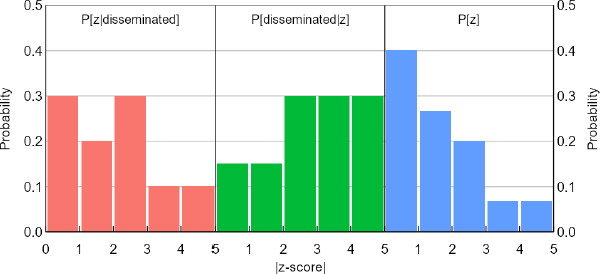
Note: These are possible versions of P[disseminated|z] and P[z] that, according to Bayes' rule, imply a bimodal distribution for P[z|disseminated].
At a high level, the approach of our 2 pattern recognition methods is to investigate whether unbiased candidates for P[z] and realistic forms of P[disseminated|z] can explain estimates of P[z|disseminated]. Unexplained variation in P[z|disseminated], especially if it is systematic, and shows up near important significance thresholds, is attributed to researcher bias.
3.2 The p-curve requires weak assumptions but produces many false negatives
The p-curve method works in 3 steps:
- Assume that the conditional probability of dissemination, P[disseminated|z], is the same for all statistically significant values of z (as in the middle panel in Figure 2). In other words, the chances of dissemination are the same for all statistically significant test statistics. Estimates of P[z|disseminated] for these z are then just rescaled estimates of P[z]. The p-curve method makes no assumptions about P[disseminated|z] for insignificant values of z, discarding all test statistics in this range.
- Translate this estimated P[z] segment into its p-value equivalent, P[p]. (Hence the name p-curve.) This translation helps because, without researcher bias, a P[p] segment should take only one of two distinctive forms. The first form is a P[p] that is uniform over p, which corresponds to the extreme case in which null hypotheses are always true. This result holds by definition of the p-value, in that whenever a null hypothesis is true, p < 0.01 should occur 1 per cent of the time, p < 0.02 should occur 2 per cent of the time, and so on. The second form is a P[p] that decreases over p, which corresponds to the case in which at least one alternative hypothesis is true. A value of p < 0.01 should, for example, occur more than 1 per cent of the time in this case. A third form, in which P[p] increases over p, corresponds to neither and should never occur without researcher bias. But a key realisation of Simonsohn et al (2014) is that, with researcher bias, P[p] can take all 3 forms (Figure 3). The high-level idea behind this possibility of an increasing P[p] is that a biased quest for statistical significance is likely to stop as soon as the 5 per cent threshold is passed. Researchers are ‘unlikely to pursue the lowest possible p’ (Simonsohn et al 2014, p 536). So trespassing test statistics will be concentrated in the just-significant zone.
- Test the hypothesis that P[p] increases over p against the null that P[p] is uniform over p. A one-sided rejection indicates researcher bias.[3]
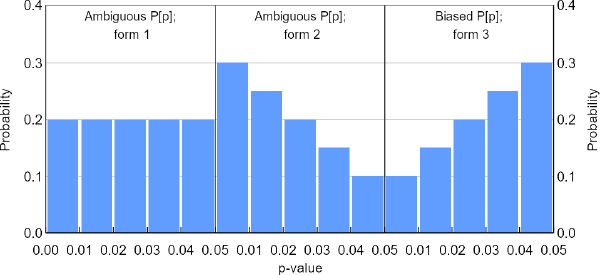
Notes: These are 3 possible forms of P[p] (called p-curves) over significant values of p. Only form 3 is unambiguous. Had this hypothetical considered insignificant results as well, the probabilities for significant p would all be scaled down, as per the explanations we offer in the body text. In the left panel, for example, the probabilities would all be 0.01.
A central shortcoming recognised by Simonsohn et al (2014) is that while P[p] can take on all 3 forms in the presence of researcher bias, the p-curve will detect only cases in which P[p] increases over p. And unless the hypothesis tests in the population of interest have very low statistical power, P[p] will increase over p only when researcher bias is pervasive. Thus, the p-curve has a high propensity to generate false negatives.[4]
3.3 The z-curve produces fewer false negatives but requires strong assumptions
The z-curve method works in 4 steps:
- Identify a wide range of potential candidates for bias-free forms of P[z]. Brodeur et al (2016) choose these candidates by combining several selection criteria, one being that the tail of the z distribution should be longer than for the standard normal distribution. The idea is to capture the fact that researchers will not always be testing hypotheses for which the null is true. (True null hypotheses correspond to a distribution of test statistics that is asymptotically standard normal.) Their chosen candidates include empirical distributions that come from collating test statistics on millions of random regressions within 4 economic datasets: the World Development Indicators (WDI), the Quality of Government (QOG) dataset, the Panel Study of Income Dynamics (PSID) and the Vietnam Household Living Standards Survey (VHLSS). These distributions of random test statistics will be free of researcher bias, by construction. Other candidate distributions are parametric, and include various Student-t and Cauchy forms.
- Select several preferred candidates for P[z], based on how well each matches the estimated distribution of P[z|disseminated] for values of z larger than 5. This introduces an assumption that both researcher and dissemination bias should be ‘much less intense, if not absent’, over these extreme values of z (Brodeur et al 2016, p 17). If true, P[z|disseminated] is indeed an undistorted representation of the bias-free form of P[z] over this range. Matching the candidates for P[z] to the estimated distribution for P[z|disseminated] is an informal process, leaving room for judgement.
- For each of these preferred candidates of P[z], choose a corresponding P[disseminated|z] that increases in z and best explains the observed draws from P[z|disseminated]. ‘Best’ here is determined by a least squares criterion, and P[disseminated|z] is increasing to capture the idea that researchers are more likely to discriminate against insignificant results than significant ones. The goal here is to explain as much of the estimated P[z|disseminated] distribution as possible with plausible forms of dissemination bias.
- Attribute all unexplained variation in P[z|disseminated] to researcher bias, especially if it suggests a missing density of results just below the 5 per cent significance threshold that can be retrieved just above it. The formal estimate of researcher bias is the maximum excess of results above the 5 per cent statistical significance threshold of |z| = 1.96. Brodeur et al (2016) offer separate estimates of researcher bias for each chosen P[z] candidate, although the variation across their estimates is small. In contrast to the p-curve, the z-curve does not culminate in a formal hypothesis test.
A potential problem raised by Brodeur et al (2016) is that dissemination bias might not be so simple as to always favour more statistically significant results; tightly estimated null results might be sought after. To address this concern, they try dropping from their sample all research that produces tightly estimated nulls and highlights them in text as being a key contribution. Reassuringly, their estimates of bias in top journals are robust to this change. Brodeur et al also point out that their sample of test statistics will be clustered at the paper level. They try weighting schemes that de-emphasise papers with many results, finding the change to make little difference.
We worry most about whether the method generates suitable guesses for the shape of unbiased P[z]; the true shape would be the result of many interacting and unobservable factors, and incorrect guesses could plausibly affect findings about researcher bias. One particular concern is that unfiltered samples of test statistics, like the one in Brodeur et al (2016), will include research that is transparent about using data-driven model selection techniques, such as general-to-specific variable selection. Those techniques could plausibly generate a bunching of just-significant results and thus contribute automatically to findings of researcher bias, despite being disclosed. Leeb and Pötscher (2005) explain that common data-driven model selection techniques can distort test statistics in unpredictable ways.
3.4 We test the merits of the z-curve
We investigate our main concern with the z-curve by pursuing 2 new lines of analysis.
First, we try cleansing our sample of test statistics from subpopulations that we think are most likely to breach the method's assumptions. In particular, we drop statistics that authors disclose as coming from a data-driven model selection process. We also drop results that are proposed answers to ‘reverse causal’ research questions, meaning they study the possible causes of an observed outcome (see Gelman and Imbens (2013)). An example would be the question ‘why is wage growth so low?’, and our logic for dropping the results is that data-driven model selection is often implied. For the same reason, we also drop a handful of test statistics produced by estimates of general equilibrium macroeconometric models. Our remaining test statistics then come from what authors portray to be ‘forward causal’ research, meaning research that studies the effects of a pre-specified cause. An example would be research that focuses on the question ‘what is the effect of unionisation on wages?’ We do not try the same change for the top journals dataset because it does not contain the necessary identifiers, and we have not collected them ourselves. (To be clear, neither of the panels in Figure 1 apply these data cleanses. Our comparisons are always like for like.)
Second, we introduce a placebo exercise that applies the z-curve method to a sample of test statistics on control variables. If the z-curve method is sound, it should not find researcher bias in these test statistics. Mechanisms that could motivate the bias are missing because the statistical significance of control variables is not a selling point of research. Brodeur et al (2016) did not include test statistics about control variables in their analysis for this very reason.
To conduct our placebo exercise, we drop tests that do not capture a specific economic hunch or theory, such as tests of fixed effects or time trends. We also drop results that authors disclose as coming from data-driven model selection and results that address a reverse causal question.[5] We cannot apply the same placebo test to top journals though, because we have not collected the necessary data.
4. Our Summary Statistics Show Important Institutional Differences
The new central bank dataset contains around 15,000 hypothesis tests from 190 discussion papers that were released from 2000 to 2019 (Table 1). Around 13,000 hypothesis tests are of primary interest, meaning they represent a main result of a paper. The rest pertain to control variables. The dataset also contains other information about the papers, such as authorship, data and code availability, and journal publication.
| RBA | RBNZ | Minneapolis Fed | Central banks combined | Top journals | |
|---|---|---|---|---|---|
| Results by paper | |||||
| Total number | 75 | 59 | 56 | 190 | 641 |
| Share of which: | |||||
| Make data and code available | 15 | 0 | 14 | 10 | 46 |
| Had authors other than central bankers | 11 | 32 | 68 | 34 | na |
| Were also published in peer-reviewed journal | 28 | 31 | 64 | 39 | 100 |
| Average number of authors per paper | 2.1 | 1.8 | 2.2 | 2.0 | 2.2 |
| Results by test statistic: main | |||||
| Total number | 4,901 | 5,589 | 2,569 | 13,059 | 50,078 |
| Share of which: | |||||
| Use ‘eye catchers’ for statistical significance | 77 | 89 | 57 | 78 | 64 |
| Portrayed as ‘forward causal’ research | 67 | 68 | 93 | 73 | na |
| Disclose using data-driven model selection | 20 | 7 | 2 | 11 | na |
| Results by test statistic: control | |||||
| Total number | 957 | 185 | 607 | 1,749 | 0 |
|
Notes: Papers that make data and code available are only those for which the central bank website contains the data and code or a link to them; we do not count cases in which code is accessible by other means. By ‘forward causal’ we mean research that studies the effects of a pre-specified cause, as per Gelman and Imbens (2013). Excluded from this category are ‘reverse causal’ research questions, which search for possible causes of an observed outcome. We also excluded a few papers that are straight forecasting work and a few instances of general equilibrium macroeconometric modelling. Data-driven model selection includes, for example, a general-to-specific variable selection strategy. ‘Eye catchers’ include stars, bold face, or statistical significance comments in the text. We use ‘Top journals’ as loose shorthand for The American Economic Review, the Journal of Political Economy, and The Quarterly Journal of Economics. Sources: Authors' calculations; Brodeur et al (2016); Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand |
|||||
The central banks released a further 540 discussion papers in this time period, but we excluded them because they did not have the right types of hypothesis tests. We required that hypothesis tests apply to single model coefficients, use t-statistics, be two-sided, and have zero nulls. We excluded 83 per cent of papers from the Minneapolis Fed, 66 per cent of papers from the RBA and 68 per cent of papers from the RBNZ. The Minneapolis Fed has the highest exclusion rate because it produced more theoretical research.
Five aspects of the summary statistics might prompt productive institutional introspection:
-
Compared with articles in top journals, fewer central bank discussion papers were released with access to data and code. We collected this information because, when contracts allow it, providing data and code sufficient to replicate a paper's results is best practice (Christensen and Miguel 2018). The top journals all have policies requiring this form of transparency; The American Economic Review introduced its policy in 2005, the Journal of Political Economy in 2006, and The Quarterly Journal of Economics in 2016. Of the central banks, only the RBA has a similar policy for discussion papers, which it introduced in 2018.
A benign explanation for central banks' lower research transparency levels might be the preliminary status of discussion papers. Central bank researchers might also rely more on confidential datasets.[6]
- The central banks show large differences in their levels of collaboration with external researchers. External collaboration was most prevalent at the Minneapolis Fed, where many of the collaborators were academics.
- A far larger share of Minneapolis Fed papers were published in peer-reviewed journals, consistent with its higher collaboration levels and our subjective view of differences in (informal) publication incentives.[7]
- The RBA and RBNZ papers emphasised statistical significance more often than the Minneapolis Fed papers or articles in top journals. The typical emphasis used stars or bold face numbers in results tables or mentions in body text. Current American Economic Association guidelines ask authors not to use stars, and elsewhere there are calls to retire statistical significance thresholds altogether, partly to combat researcher bias (e.g. Amrhein, Greenland and McShane 2019).
- Staff at the RBA and RBNZ focused more on research that was reverse causal, and less on research that was forward causal, than did staff at the Minneapolis Fed. As explained by Gelman and Imbens (2013), both types of questions have important roles in the scientific process, but the distinction is important. The reason is that, while reverse causal questions are a natural way for policymakers to think and important for hypothesis generation, they are also inherently ambiguous; finding evidence favouring one set of causes can never rule out others, so complete answers are impossible. Another challenge is that reverse causal research often generates its hypotheses using the same datasets they are tested on. This feature makes the research unusually prone to returning false positives.
The top journals dataset contains about 50,000 test statistics from 640 papers that were published between 2005 and 2011 in The American Economic Review, Journal of Political Economy and The Quarterly Journal of Economics. It includes many of the same variables as the central bank dataset. It also excludes many papers for the same reasons the central bank dataset does. A potentially important difference is that the central bank dataset covers a longer time window to ensure an informative sample size.
Simonsohn et al (2014) advise that, to implement the hypothesis test from the p-curve method properly, the sample should contain statistically independent observations. So, for the p-curve, we use one randomly chosen result from each paper; doing so leaves us with 185 central bank observations and 623 top journal observations.[8] Simonsohn et al use far smaller sample sizes. For the z-curve, we use complete samples.
5. Our Findings Do Not Call for Changes in Research Practices
5.1 The p-curve produces no evidence of bias
Using the p-curve method, we do not find any statistical evidence of researcher bias in our central bank sample. In fact, the p-curve shows an obvious downward slope (Figure 4). We get the same qualitative results when applying the p-curve to the top journals dataset, even though Brodeur et al (2016) do find evidence of researcher bias when applying the z-curve to that dataset. While our finding is consistent with the p-curve's high propensity to produce false negatives, it is not necessarily an example of one.
Our pre-analysis plan also specifies p-curve assessments of several subgroups, and includes several methodological robustness checks. The results are all the same: we find no evidence of researcher bias, since the p-curves all slope downward. We have little more of value to say about those results, so we leave the details to our online appendix.
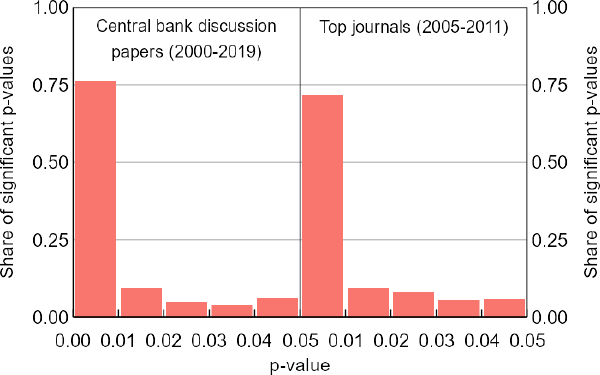
Note: The observed p-curves from both samples are clearly downward sloping, a result that does not suggest researcher bias.
Sources: Authors' calculations; Brodeur et al (2016); Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
5.2 The z-curve results show just as much bias at central banks as at top journals
For central banks, the observed distribution of z-scores for the main results (not the controls), and without any of our sample changes, is unimodal (Figure 1). For top journals, the equivalent distribution is bimodal. The difference matters because it is the bimodal shape that motivates the z-curve decomposition conducted by Brodeur et al (2016). The difference is thus evidence suggestive of differences in researcher bias.
The formal results of the z-curve in Table 2, however, show roughly as much researcher bias at central banks as in top journals. The number 2.3 in the first column of data technically reads as ‘assuming that the bias-free form of P[z] is the Cauchy distribution with 1.5 degrees of freedom, and P[disseminated|z] is well estimated non-parametrically, there is an unexplained excess of just-significant results that amounts to 2.3 per cent of all results’. The excess is what Brodeur et al (2016) attribute to researcher bias, so higher numbers are worse. The result is meant to be conservative because the z-curve method tries to explain as much of P[z|disseminated] as possible with dissemination bias. The empty cells in Table 2 correspond to what turned out to be poor candidates for bias-free P[z], as judged by Step 2 of the z-curve method.
| Assumed P[z] | Central banks | Top journals | |||
|---|---|---|---|---|---|
| Non-parametric estimate of P[disseminated|z] | Parametric estimate of P[disseminated|z] | Non-parametric estimate of P[disseminated|z] | Parametric estimate of P[disseminated|z] | ||
| Standard | |||||
| Student-t(1) | 1.7 | 2.5 | |||
| Cauchy(0.5) | 1.1 | 1.6 | |||
| Cauchy(1.5) | 2.3 | 2.9 | |||
| Empirical | |||||
| WDI | 2.2 | 2.7 | 2.7 | 3.0 | |
| VHLSS | 1.8 | 2.0 | 2.0 | 2.0 | |
| QOG | 1.2 | 1.7 | 1.4 | 2.0 | |
| PSID | 1.4 | 2.3 | |||
|
Notes: The number 2.3 in the first column of data reads as ‘there is an unexplained excess of just-significant results that amounts to 2.3 per cent of all results’. The z-curve method attributes this excess to researcher bias. We drop one-sided tests from the Brodeur et al (2016) sample, but the effect is negligible. The empty cells correspond to what turned out to be poor candidates for bias-free P[z], as per our pre-analysis plan. Sources: Authors' calculations; Brodeur et al (2016); Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand |
|||||
Brodeur et al (2016) support their main results with many figures, including several that (i) justify their choices for bias-free forms of P[z], (ii) show their estimated functional forms for P[disseminated|z], and (iii) show the cumulative portions of estimated P[z|disseminated] that cannot be explained with P[z] and P[disseminated|z]. These last ones plot the supposed influence of researcher bias. In our work, the most interesting finding from the equivalent sets of figures is that we generate all of the results in Table 2 using sensible functional forms for P[disseminated|z]. For example, the functional forms that we estimate non-parametrically all reach their peak (or almost reach it) at the |z| = 1.96 threshold and are little changed over higher values of absolute z. This is consistent with the assumption in both methods that P[disseminated|z] is not a source of distortion for high absolute z. To simplify and shorten our paper, we leave these extra figures to our online appendix.
5.3 Our extensions cast doubt on the z-curve method
Within our central bank sample, hypothesis tests disclosed as coming from data-driven model selection or reverse causal research yield distributions of test statistics that look quite different from the rest (Figure 5). None of the distributions show obvious anomalies, but had central banks done more data-driven model selection or reverse causal research, the combined distribution in the left panel of Figure 1 could plausibly have been bimodal as well. Likewise, the observed bimodal shape for the top journals might occur because they have a high concentration of data-driven model selection and reverse causal research; we just do not have the necessary data to tell. Unsurprisingly, these types of test statistics also exaggerate our formal z-curve results; if we apply the z-curve method to the central bank sample that excludes data-driven model selection and reverse causal research, our bias estimates fall by about a third (Table 3).
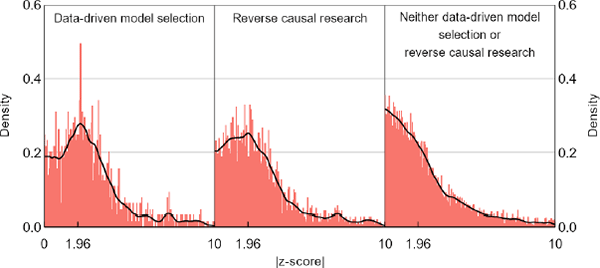
Notes: Data-driven model selection and reverse causal research are overlapping categories. None of the distributions show obvious anomalies, but if they were blended with different weights, they could plausibly produce a bimodal aggregate.
Sources: Sources: Authors' calculations; Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
| Assumed P[z] | Main sample excluding data-driven model selection and reverse causal research | Placebo sample on control variable parameters | |||
|---|---|---|---|---|---|
| Non-parametric estimate of P[disseminated|z] | Parametric estimate of P[disseminated|z] | Non-parametric estimate of P[disseminated|z] | Parametric estimate of P[disseminated|z] | ||
| Standard | |||||
| Cauchy(0.5) | 1.6 | 2.2 | 2.1 | 1.7 | |
| Cauchy(1.5) | 3.4 | 2.8 | 2.4 | 2.6 | |
| Empirical | |||||
| WDI | 1.5 | 1.9 | 2.1 | 1.7 | |
| VHLSS | 1.2 | 1.4 | 2.2 | 1.5 | |
| QOG | 0.7 | 1.1 | 2.0 | 0.8 | |
|
Notes: The number 1.6 in the first column of data reads as ‘there is an unexplained excess of just-significant results that amounts to 1.6 per cent of all results’. The z-curve method attributes this excess to researcher bias. The placebo sample is at a size that Brodeur et al (2016) say is too small to reliably use the z-curve method. Acknowledging that, it produces just as much measured researcher bias as the cleansed main sample. We add results that correspond to a Cauchy distribution with 0.5 degrees of freedom for P[z] because the observed test statistics here show thicker tails than for the main sample. This is especially true of the control variables distribution. Sources: Authors' calculations; Brodeur et al (2016); Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand |
|||||
Our placebo exercise also casts doubt on the z-curve method. Our sample of controls is around sizes that Brodeur et al (2016) regard as too small to reliably use the z-curve method, so the controls distribution of test statistics is noisier than the others (Figure 6) and our placebo test is only partial. In any event, our formal z-curve results for the controls sample show just as much researcher bias as for the main sample, after we exclude from it results produced by data-driven model selection or reverse causal research (Table 3). Ideally, the tests would have shown no measured researcher bias, because there is no incentive to produce statistically significant results for control variables. It is thus difficult to attribute the formal z-curve results for our central bank sample to researcher bias.
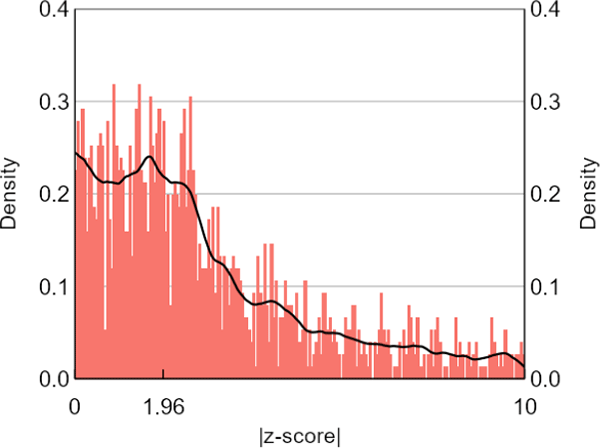
Sources: Authors' calculations; Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
5.4 Differences in dissemination bias might be important here
What then might explain the differences between our sample distributions of z-scores for the central banks and top journals? The differences must come from P[disseminated|z], unbiased P[z], researcher bias, sampling error, or some combination of these factors, but we have insufficient evidence to isolate which. There is a lot of room for speculation here and, judging by our conversations with others on this topic, a strong appetite for such speculation as well. Here, we restrict our comments to the few we can support with data.
As per the stylised scenario in Figure 2, one possible explanation for the bimodal shape of the top journals distribution could be a steep increase in P[disseminated|z] near significant values of z. Likewise, the absence of bimodality at the central banks might reflect a shallower increase in P[disseminated|z].[9] The z-curve method does produce estimates of P[disseminated|z] – as part of Step 3 – and they are consistent with this story (Figure 7). However, the problems we have identified with the z-curve method would affect these estimates as well.
![Figure 7: Comparisons of Estimated P[disseminated|z]](images/figure-7.gif)
Notes: The panels show estimated functions for P[disseminated|z] for different versions of P[z], but always using the non-parametric estimation method outlined in Brodeur et al (2016). The probabilities have also been indexed to 100 at |z| = 1.96 to facilitate comparison. The estimated functions are steeper in the almost-significant zone for top journals than they are for central banks.
Sources: Authors' calculations; Brodeur et al (2016); Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
Whatever the sources of the distributional differences, they are unlikely to stem from central banks focusing more on macroeconomic research, at least as broadly defined. Brodeur et al (2016) show a sample distribution that uses only macroeconomic papers, and it too is bimodal. In fact, bimodality features in just about all of the subsamples they present.
We also doubt that the sources of the distributional differences could apply equally to the 3 central banks we analyse. Noting that our sample sizes for each of them are getting small, the data for the Minneapolis Fed look like they come from a population with more mass in high absolute z (Figure 8). This right-shift is consistent with our subjective view of differences in publication incentives, but since our summary statistics show that the Minneapolis Fed stands out on several other dimensions as well, we are reluctant to push this point further. Moreover, restricting our central bank sample to papers that were subsequently published in journals does not produce a distribution noteworthy for its right-shift (Figure 9). This result surprised us. Further work could investigate whether the journal versions of these same papers produce noticeable distributional shifts. O'Boyle, Banks and Gonzalez-Mulé (2017) do a similar exercise in the field of management, finding that the ratio of supported to unsupported hypotheses was over twice as high in journal versions of dissertations than in the pre-publication versions.
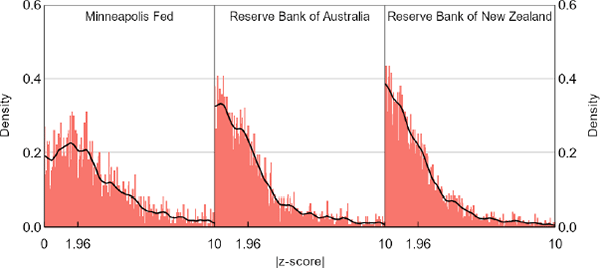
Sources: Authors' calculations; Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
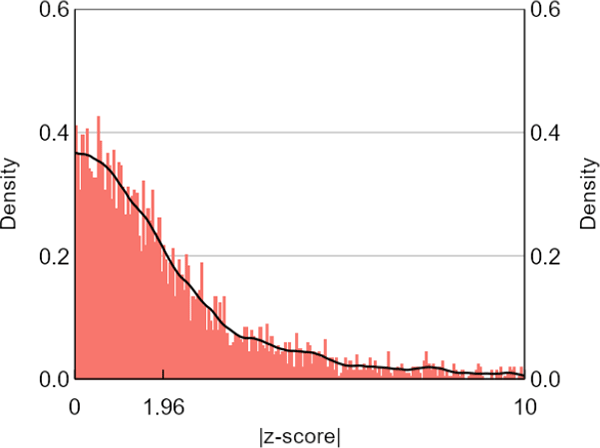
Note: Restricting the central bank sample to papers that were subsequently published in journals does not produce a distribution of test statistics that is noteworthy for its right-shift.
Sources: Authors' calculations; Federal Reserve Bank of Minneapolis; Reserve Bank of Australia; Reserve Bank of New Zealand
6. We Were Able to Replicate the Original Papers
We started this work with an attempt to replicate the findings of Simonsohn et al (2014) and Brodeur et al (2016), using their data and code. Since replication results now attract broader interest, we provide them in Appendix B. The bottom line is that the supplementary material for both papers was excellent, and we were able to replicate the findings without material error. The authors of both papers promptly answered questions.
Conclusion
There are now many studies claiming to show that common research practices have been systematically producing misleading bodies of evidence. Several fields have been implicated, including finance and economics. To date, the claims have focused mainly on work published in peer-reviewed journals, with one of the alleged problems being researcher bias. There are now growing calls to adopt research practices that, while often resource intensive, better preserve research credibility.
We search for researcher bias in a different population of interest: central banks. Whereas Fabo et al (2020) do show evidence suggesting researcher bias in central bank assessments of quantitative easing, our focus on a broader body of central bank research produces results that are mixed. What's more, the part of our work that does suggest bias uses a method that we challenge. At this point, all that is clear from our work is that central banks produce results with patterns different from those in top economic journals; there is less bunching around the 5 per cent threshold of statistical significance. We offer some speculative explanations for the difference but ultimately leave it as a puzzle for future research to explain.
Appendix A : Credibility Safeguards
This project had the potential to produce controversial results. To avoid putting strain on professional relationships between central banks, we included only the central banks with which co-authors on the project were affiliated. A downside of this approach is that it created a conflict of interest. The conflict could have fostered bias of our own, which would have been deeply hypocritical.
To support the credibility of the work, we have done the following:
- We have released the data we collected and statistical programs we use.
- We have swapped central banks in the data collection, so that none of the collectors gathered data from the central banks with which they were affiliated.
- We have identified who collected each data point in our dataset.
- We have declared the conflict of interest at the start of this paper.
- We have publicly registered a pre-analysis plan on the Open Science Framework website www.osf.io (available at <https://doi.org/10.17605/OSF.IO/K3G2F>). We note that pre-analysis plans are rarely used for observational studies because of difficulties in proving that the plans have been written before data analysis. Burlig (2018) lists scenarios in which credibility is still achievable, but we fit poorly into those because our data are freely available. Credibility in our case rests on our having registered the plan before we undertook the large task of compiling the data into a useful format.
There are several parts where we have deviated from our plan:
- Our language has changed in some important places, in response to feedback. Firstly, our definition of researcher bias is now more precise. Our plan had used the definition ‘a tendency to present the results of key hypothesis tests as having statistical significance when a fair presentation would not have'. Secondly, our plan used the names exploratory and confirmatory for what we now label as reverse causal and forward causal. The new language is less loaded and consistent with other work on the topic. Our descriptions of the concepts are the same though.
- In our plan, we intended to cleanse the top journals dataset of data-driven model selection and reverse causal research in an automated way, using keywords that we identified as being sensible indicators while collecting the central bank data. But when collecting the data, it became clear that our best keywords would produce too many false signals. We stopped the initiative, believing that even our best efforts would produce results that were not credible. This saved the research team a lot of time.
- We did not include the placebo test in our pre-analysis plan. We have the necessary data on hand only because, following a suggestion in footnote 19 of Brodeur et al (2016), we had planned to use the controls as a sensible candidate for bias-free P[z]. In the end, the distribution of controls turned out to have too much mass in the tails to meet the informal criteria in Step 2 of the z-curve method. Many aspects of the formal bias estimate were nonsense, including a maximum excess of results at low absolute z. The online appendix contains more detail.
- In Table 1, we provided more summary statistics than we had in our plan. We had not planned to show breakdowns at an institutional level on anything other than the number of papers and test statistics in our sample. We had also not planned to include the detail about co-authorship. These changes were a response to feedback.
- When writing our plan, we failed to anticipate that neither of our research question categories – reverse causal and forward causal – would neatly fit hypothesis tests in straight forecasting work. Our categories are also a bit awkward for general equilibrium macroeconometric modelling. There were very few papers of these kinds, and to be conservative, we put them into the reverse causal category (they are thus dropped from the cleansed sample).
- Though we had planned to show estimated levels of dissemination bias in central bank research, we had not planned to compare them with those of the top journals, as we did in Figure 7. Again, this was a response to feedback.
Appendix B : Replicating Simonsohn et al (2014) and Brodeur et al (2016)
In our reproduction of Brodeur et al (2016), we found only minor problems:
- The paper presents many kernel densities for distributions of test statistics, which it characterises as having a ‘two-humped’ camel shape. The kernel densities do not have any boundary correction, even though the test statistics have a bounded domain. The first hump in the camel shape is in many cases just an artefact of this error. This problem has no effect on the paper's key quantitative conclusions. Moreover, the raw distributions are pictured, providing full transparency.
- Whenever a paper showed only point estimates and standard errors, the authors infer z-scores assuming a null hypothesis of zero and a two-sided alternative hypothesis. But 73 of these cases have non-zero null hypotheses and/or one-sided alternative hypotheses, meaning the inferred z-scores are incorrect. The effects of this problem are trivial because the tests in question make up less than 0.2 per cent of the sample. Note that whenever we present results from the top journals sample, we drop these incorrect scores.
- The results presented in Table 2 of Brodeur et al (2016) differ noticeably from the output of their code (hence why the results presented in our Table 2, some of which are meant to line up with Table 2 of Brodeur et al, look different). We attribute this discrepancy to transcription error, because elsewhere in their paper, any discrepancies between their code output and published tables are trivial. The errors in Table 2 of Brodeur et al are not systematically positive or negative, and do not affect the main conclusions.
- The authors claim that ‘[n]onmonotonic patterns in the distribution of test statistics, like in the case of a two-humped shape, cannot be explained by selection alone’ (p 11). This statement is incorrect, as we illustrate in Figure 2 of this paper. Since the two-humped shape features prominently in their paper, we feel it worthy of discussion here. In other parts of their paper, most notably Section IV, the authors seem to recognise that a two-humped shape can be explained by selection. So we discuss the issue here only as a matter of clarification.
We successfully replicated the results of Simonsohn et al (2014) using a web-based application that the authors make available (version 4.06) and their two datasets (obtained via personal communication). The only differences were immaterial and we think attributable to slight improvements to the web application (see Simonsohn, Simmons and Nelson (2015) for details). The authors provided us with their data soon after our request.
References
Allen F, C Bean and J De Gregorio (2016), ‘Independent Review of BIS Research: Final Report’, 23 December.
Amrhein V, S Greenland and B McShane (2019), ‘Scientists Rise up against Statistical Significance’, Nature, 567(7748), pp 305–307.
Bartoš F and U Schimmack (2021), ‘Z-Curve.2.0: Estimating Replication Rates and Discovery Rates’, PsyArXiv, accessed 9 January 2021, doi: 10.31234/osf.io/urgtn.
Blanco-Perez C and A Brodeur (2020), ‘Publication Bias and Editorial Statement on Negative Findings’, The Economic Journal, 130(629), pp 1226–1247.
Brodeur A, N Cook and A Heyes (2020), ‘Methods Matter: p-Hacking and Publication Bias in Causal Analysis in Economics’, The American Economic Review, 110(11), pp 3634–3660.
Brodeur A, M Lé, M Sangnier and Y Zylberberg (2016), ‘Star Wars: The Empirics Strike Back’, American Economic Journal: Applied Economics, 8(1), pp 1–32.
Brunner J and U Schimmack (2020), ‘Estimating Population Mean Power under Conditions of Heterogeneity and Selection for Significance’, Meta-Psychology, 4, Original Article 3.
Burlig F (2018), ‘Improving Transparency in Observational Social Science Research: A Pre-Analysis Plan Approach’, Economics Letters, 168, pp 56–60.
Christensen G and E Miguel (2018), ‘Transparency, Reproducibility, and the Credibility of Economics Research’, Journal of Economic Literature, 56(3), pp 920–980.
Fabo B, M Jančoková, E Kempf and L Pástor (2020), ‘Fifty Shades of QE: Conflicts of Interest in Economic Research’, NBER Working Paper No 27849.
Franco A, N Malhotra, and G Simonovits (2014), ‘Publication Bias in the Social Sciences: Unlocking the File Drawer’, Science, 345(6203), pp 1502–1505.
Frankel A and M Kasy (2020), ‘Which Findings Should Be Published?’, Unpublished manuscript, 27 September. Available at <https://maxkasy.github.io/home/files/papers/findings.pdf>.
Gelman A and G Imbens (2013), ‘Why Ask Why? Forward Causal Inference and Reverse Causal Questions’, NBER Working Paper No 19614.
Haldane AG (2018), ‘Central Bank Psychology’, in P Conti-Brown and RM Lastra (eds), Research Handbook on Central Banking, Edward Elgar Publishing Limited, Cheltenham, pp 365–379.
Ioannidis JPA (2005), ‘Why Most Published Research Findings Are False’, PLoS Medicine, 2(8), e124, pp 0696–0701.
Leeb H and BM Pötscher (2005), ‘Model Selection and Inference: Facts and Fiction’, Econometric Theory, 21(1), pp 21–59.
Obermeyer Z, B Powers, C Vogeli and S Mullainathan (2019), ‘Dissecting Racial Bias in an Algorithm Used to Manage the Health of Populations’, Science, 366(6464), pp 447–453.
O'Boyle EH Jr, GC Banks and E Gonzalez-Mulé (2017), ‘The Chrysalis Effect: How Ugly Initial Results Metamorphosize into Beautiful Articles’, Journal of Management, 43(2), pp 376–399.
Simonsohn U, LD Nelson and JP Simmons (2014), ‘P-curve: A Key to the File-Drawer’, Journal of Experimental Psychology: General, 143(2), pp 534–547.
Simonsohn U, JP Simmons and LD Nelson (2015), ‘Better P-curves: Making P-curve Analysis More Robust to Errors, Fraud, and Ambitious P-hacking, a Reply to Ulrich and Miller (2015)’, Journal of Experimental Psychology: General, 144(6), pp 1146–1152.
Simonsohn U, JP Simmons and LD Nelson (2020), ‘Specification Curve Analysis’, Nature Human Behaviour, 4(11), pp 1208–1214.
Acknowledgements
We thank Cristian Aguilera Arellano for research assistance. For their comments, we thank Hang Banh, Anthony Brassil, Iris Chan, Anna Dreber, Luci Ellis, Denzi Fiebig, Kevin Fox, Mathias Lé, Uri Simonsohn, Michelle van der Merwe, Melissa Wilson and participants at several seminars. James Holt and Paula Drew gave editorial assistance. Adam Gorajek and Andrew Staib acknowledge Australian Government Research Training Program Scholarships. The views in this paper are those of the authors and do not necessarily reflect the views of the Federal Reserve Bank of Minneapolis, the Federal Reserve System, the Reserve Bank of Australia or the Reserve Bank of New Zealand. Any errors are the sole responsibility of the authors.
Declaration: We are affiliated with the central banks we investigate and thus have a conflict of interest. To protect the credibility of this work, we registered a pre-analysis plan with the Open Science Framework before we collected data. Appendix A explains where to find the plan, discloses our deviations from the plan, and lists other credibility safeguards that we used.
Footnotes
Brunner and Schimmack (2020) and Bartoš and Schimmack (2021) offer another method, also called the z-curve. It aims to understand whether the findings in a body of work are replicable, whereas our objective is solely to understand researcher bias. [1]
Scholars disagree about whether dissemination bias alone would be problematic. Frankel and Kasy (2020) offer a careful assessment of the trade-offs, albeit ignoring possible spillovers into researcher bias. [2]
Equivalent tests could be conducted without converting the distribution to p-values. The advantage of converting to p-values is that the benchmark distribution takes on a simple and distinctive uniform shape. [3]
The p-curve method as it appears in Simonsohn et al (2014) contains another test, which is about whether the research in question has less power than an underpowered benchmark. The aim is to understand whether the research has ‘evidential value’. We skip this exercise because our research question focuses on other matters. Moreover, Brunner and Schimmack (2020) have challenged this other test's merits. [4]
Of the few departures from our pre-analysis plan (all listed in Appendix A), conducting this placebo test is the most important. [5]
Even in this case, researchers can attain high levels of transparency by releasing synthetic data. One such example is Obermeyer et al (2019). [6]
Our measures understate true publication rates because the papers released in the back end of our window might publish after we collected data (January 2020). The problem is unlikely to drive the relative standings though. [7]
Our plan specifies a random seed for our pseudo-random number generator. A reader has since suggested that we test over several different random samples. We do not present the results of that exercise, because the test statistics (we used p-values) in every sample were indistinguishable from one another at two decimal places. [8]
Dissemination is defined by the dataset being used. In the top journals dataset, dissemination refers to publication in a top journal, while in the central banks dataset, dissemination refers to inclusion in a discussion paper that has been released on a central bank's website. [9]