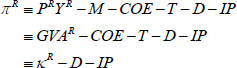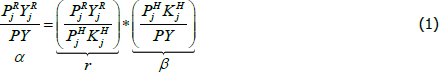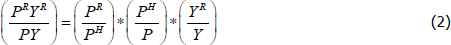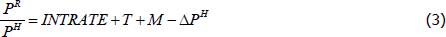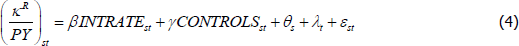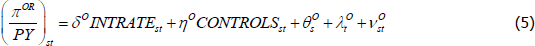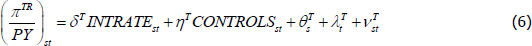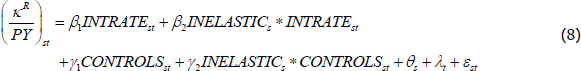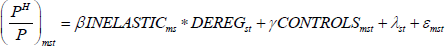Research Discussion Paper – RDP 2016-04 Housing Prices, Mortgage Interest Rates and the Rising Share of Capital Income in the United States
1. Introduction
I believe that the right model to think about rising capital-income ratios and capital shares in recent decades is a multi-sector model of capital accumulation, with substantial movements in relative prices … [i]ndeed, large upward or downward movements of real estate prices play an important role in the evolution of aggregate capital values during recent decades Piketty 2016
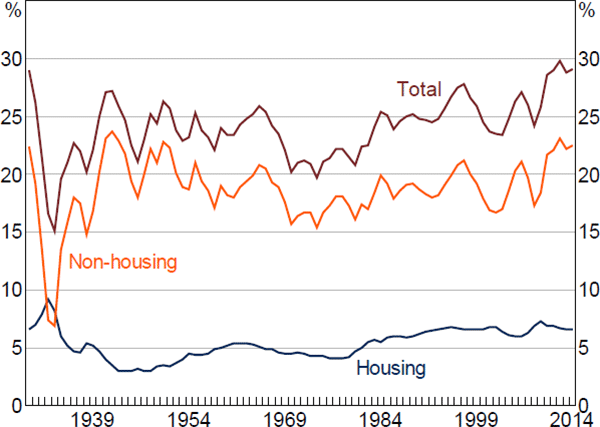
Piketty (2014) documents how the share of aggregate income going to capital in the United States (and other advanced economies) followed a U-shaped pattern in the post-war era; it fell between the 1940s and 1970s but has risen since then.[1] Rognlie (2015) has subsequently shown that much of the rise in the net capital income share in the post-war era is due to the housing sector (Figure 1). The share of total income going to the owners of housing capital (or ‘rental income’) in the United States gradually rose from around 3 per cent in 1950 to 7 per cent in 2014.
Notes: Net capital income is equal to net operating surplus, or gross operating surplus less depreciation; net domestic income is equal to gross domestic product less total depreciation
Sources: Author's calculations; Bureau of Economic Analysis; Piketty and Zucman (2014)
The long-run rise in the share of spending on housing in the US economy is not specific to the national accounts, but can be observed across a range of household surveys, including the American Housing Survey, the Census and the Consumer Expenditure Survey (Albouy, Ehrlich and Liu 2014). The secular rise in the ‘housing capital share’ of the economy is also not specific to the United States but has occurred in almost every advanced economy over the past three decades (Rognlie 2015). The broad-based nature of the secular rise in the housing capital share – both across surveys and across countries – suggests it is not a measurement artefact but a genuine phenomenon.
The aim of this paper is to examine why the housing capital income share rose in the United States over recent decades. Structural factors such as an increase in the home ownership rate and an increase in the average size and quality of housing are important in explaining the increase in the housing capital income share in the period immediately after the Second World War. However, these structural factors appear to have been less important in explaining the ‘rise of housing’ in the period since the early 1980s.
Several research papers (e.g. Rognlie 2015; Bonnet et al 2014; Weil 2015), print articles (e.g. The Economist 2015) and blogs (e.g. Smith 2015) have hypothesised that the secular increase in the housing share of the economy over this time might be due to some combination of lower interest rates, higher mortgage debt and constraints on home building (due to either geographic constraints or land zoning restrictions). But, to the best of my knowledge, no previous study has empirically documented the links between the trend increase in the share of housing capital income on the one hand, and financial market liberalisation, mortgage interest rates and housing supply constraints on the other.
In theory, the long-run rise in the housing share of the economy is somewhat puzzling. To the extent that the consumption of housing services is a necessity, housing demand should be income inelastic; as households get richer, they should spend less on housing services. Similarly, as an economy grows, the share of aggregate spending on housing should fall, not rise. Classical studies typically pointed to evidence that the income elasticity of housing is less than unity, consistent with housing being a necessary good. But later research has pointed to more mixed evidence, with some studies finding an elasticity well above unity (Albouy et al 2014).
This empirical puzzle can be reconciled with theory by noting that a home consists of both a land component and a structure component; the building structure is a necessary good but the land is, quite literally, a ‘positional’ or luxury good (Frank 2005). So, to the extent that land is a luxury good, we might expect an increase in income to be associated with higher demand for housing services. Moreover, if there are very few substitutes for housing, and hence demand is price inelastic, then rising housing prices could cause the housing expenditure share to rise, even as income rises (Albouy et al 2014).
Along these lines, I reconcile the theory with the facts by appealing to the insensitivity of housing supply to changes in the relative price of housing in some large cities of the United States. Specifically, I argue that consumer price disinflation and the deregulation of the US mortgage market during the 1980s and 1990s acted as positive credit supply shocks (with high inflation and credit market regulation in the 1970s acting as artificial borrowing constraints). The subsequent decline in nominal interest rates lowered the cost of owning and so effectively increased the demand for housing for credit-constrained households (Ellis 2005). The resulting increase in housing demand led to higher relative prices for land in areas that are constrained in terms of new housing supply. The rise in the relative price of land, in turn, led to an increase in the (nominal) share of spending on housing. Given that housing supply constraints are typically most prevalent in the largest US cities, they contributed disproportionately to total spending on housing (and income accruing to the owners of housing) in the overall economy. While this paper focuses on the empirical evidence, Sommer, Sullivan and Verbrugge (2013) and Stiglitz (2015) outline theories that are consistent with this hypothesis.[2]
First, I document some new stylised facts about housing income and spending in the United States. I follow Piketty and Zucman (2014) and Rognlie (2015) in undertaking a detailed examination of the national accounts, but I take the further step of decomposing the data by geographic region (e.g. states and metropolitan areas) and also by different types of housing (e.g. owner-occupied and tenant-occupied). Second, I explore the determinants of the secular rise in the housing share of the economy by exploiting both cross-sectional and time-series variation in factors such as housing prices, interest rates and land supply constraints (as documented, for example, by Saiz (2010)). In a state-level panel regression framework, I test the following hypotheses:
-
H1: Lower nominal interest rates are associated with higher net housing
capital income (as a share of total income) across US states and over time:
- H1a: Lower real interest rates are associated with higher net housing capital income (as a share of total income)
- H1b: Lower consumer price inflation is associated with higher net housing capital income (as a share of total income)
- H2: The negative correlations in H1 will be strongest in US states that are constrained by housing supply.
My main findings are as follows:
- The rise in the share of housing capital income is due to an increasing share of imputed rent going to home owners (owner-occupied property) rather than an increasing share of market rent paid to landlords (tenant-occupied property).
- The rise in the share of housing capital income is due to an increase in the relative price of housing and is fully concentrated in states that are estimated to be constrained by the supply of new housing.
- The rise in the share of housing capital income is associated with long-run declines in both real interest rates and inflation, with these effects being particularly strong in supply-constrained states.
Ultimately, I argue that the rise in the share of housing capital income can be traced to an aggregate demand shock (the expansion of credit brought about by financial deregulation and disinflation), along with constraints on the supply of new homes in some large US cities.
I focus specifically on the US experience as US state-level housing markets are likely to be similar in both observable and unobservable characteristics (or at least more similar than housing markets in different countries). This limits the impact of any confounding factors and helps to pin down the causal effect of changes in interest rates and housing supply constraints on housing capital income.
Nevertheless, I suspect a similar story of financial deregulation, disinflation and housing supply constraints might explain the patterns observed in other advanced economies too, especially considering the similar timing to the United States of financial deregulation and disinflation, as well as the concentration of populations in the largest cities.
This paper is related to several strands of the literature. First, there is a large and expanding literature on the determinants of wealth and income inequality (e.g. Piketty and Zucman 2014). I will not touch directly on the issue of inequality in this paper, although the analysis reveals some interesting subtleties about the recent increase in the concentration of wealth amongst land owners; it is not landlords per se but home owners that have been ‘winning the battle’ over wealth shares, aided by lower interest rates. Second, by examining the links between financial deregulation, disinflation and housing capital income, I closely follow the extensive literature that examines the causal effect of credit supply shocks on housing prices (e.g. Ellis 2006; Favilukis, Ludvigson and Van Nieuwerburgh 2010; Duca, Muellbauer and Murphy 2011; Favara and Imbs 2015). Third, I highlight the role of housing supply constraints in driving the long-run trend increase in housing spending and hence touch on a large literature in urban economics that examines the links between land supply, housing prices and rents (e.g. Gallin 2003; Saiz 2010; Gyourko, Mayer and Sinai 2013; Hilber and Vermeulen 2016).
2. The Measurement of Housing Services
A very useful feature of the national accounts produced by the Bureau of Economic Analysis (BEA) is the ability to decompose the aggregate GDP estimates along several dimensions. For example, it is possible to decompose total housing output by the type of housing (owner-occupied and tenant-occupied) and by the type of geographic region (e.g. states and metropolitan statistical areas). To understand the drivers of the rise in housing capital income, it is important to discuss some key measurement issues (for more details on the measurement of rents and housing services in the United States, see, for example, Diewert (2003), Mayerhauser and Reinsdorf (2007), Short, O'Hara and Susin (2007) and McCarthy, Peach and Ploenzke (2010).
Housing services are a component of both household income and consumption in the national accounts. Housing services consist of two main components: 1) the rent paid by tenants to landlords (or ‘market rent’); and 2) the rent paid by home owners to themselves (or ‘imputed rent’). For the home owner, the value of housing services is measured as the income the home owner could have received if the house had been rented to a tenant. In essence, it is assumed that a home owner is paying rent to themselves as they represent both the tenant and landlord of that property. The rents imputed on owner-occupied housing are the largest component of personal consumption expenditure, valued at US$1.4 trillion in 2014 (or about 12 per cent of total personal consumption and 8 per cent of GDP). The imputation is needed for GDP to be invariant to changes in the rate of home ownership.[3]
To estimate the value for the services of owner-occupied housing, the BEA uses information on the rents charged for similar tenant-occupied housing. The imputation is based on the ‘rental equivalence’ method – the ‘gross imputed rent’ is valued by the estimated rent that a tenant would pay for the same home, taking into account factors such as dwelling size, dwelling quality, and location (Mayerhauser and Reinsdorf 2007). Importantly, this method implies that the prices (and rents) of owner-occupied and tenant-occupied housing will essentially move together over time for a given location.
As Rognlie (2015) highlights, there are important differences between ‘gross’ and ‘net’ housing services. The ‘gross output’ of housing services is the amount earned and spent on housing services, which is the same as the amount of rent paid (whether imputed or not). Gross housing output has gradually increased as a share of total net domestic income from 7.8 per cent in 1950 to 12.3 per cent in 2014. The ‘gross value added’ of the housing sector is equal to the total rent paid less expenditures on home maintenance (or ‘intermediate housing consumption’). Gross value added can be further divided into gross operating surplus (capital income), compensation of employees (labour income) and property taxes.
There are two different ways to estimate net housing income: 1) net housing capital income (or ‘net operating surplus’), which is equal to gross operating surplus less depreciation; and 2) net housing profit income (or ‘rental income of persons’), which is equal to gross operating surplus less depreciation and interest payments. Existing research tends to focus on the former measure of net housing income (e.g. Piketty and Zucman 2014; Rognlie 2015). Measured on this basis, the share of the economy going to housing capital has effectively doubled since 1950 to stand at 6.4 per cent in 2014.
I mainly focus on the long-run trends in housing capital income (κR) to be consistent with the existing research. But, I also consider housing profit income (πR) as this provides an important cross-check on the results and sheds additional light on the ultimate ‘winners’ and ‘losers’ of the secular rise in the housing share of the economy. The net profit measure has risen from 2.4 per cent of the total economy in 1950 to 3.9 per cent in 2014. It has also followed a much more pronounced U-shaped pattern over recent decades, gradually declining in the period between the Second World War and 1980 from 2.4 to 0.4 and rising thereafter.
The following accounting definition summarises the differences between the various housing income measures:
According to the BEA, net housing profit income (πR) is equal to housing gross output (i.e. the rental price, PR, multiplied by real housing services, YR) less housing maintenance (M), compensation of employees in the housing sector (COE), property taxes (T), housing depreciation (D) and mortgage interest payments (IP). Also, note that housing gross operating surplus (κR) is equal to gross value added (GVAR = PRYR − M) less compensation of employees and property taxes. The decomposition of housing services is shown in Table 1.
| 1950 | 1980 | 2014 | |
|---|---|---|---|
| Gross output of housing services (PRYR) | 7.8 | 10.0 | 12.3 |
| Less: Intermediate housing consumption (M) | 1.6 | 1.6 | 1.5 |
| Equals: Housing gross value added (GVAR) | 6.3 | 8.4 | 10.8 |
| Less: Depreciation (D) | 1.9 | 2.8 | 2.9 |
| Compensation of employees (COE) | 0.1 | 0.1 | 0.1 |
| Property taxes (T) | 1.0 | 1.7 | 1.5 |
| Equals: Housing net operating surplus (κR − D) | 3.2 | 3.9 | 6.4 |
| Less: Net mortgage interest payments (IP) | 0.8 | 3.6 | 2.3 |
| Equals: Rental income of persons (πR) | 2.4 | 0.4 | 3.9 |
| Net domestic income (US$b) | 268 | 2,471 | 14,865 |
|
Notes: ‘Gross output of housing services’ is personal consumption
expenditure on housing or, essentially, rent (both actual and imputed
rent); ‘Intermediate housing consumption’ includes expenses such as
maintenance and repairs, property insurance, brokers' commissions on land,
closing costs and property management fees; ‘Net mortgage interest
payments’ include net interest paid and net current transfer payments (or
insurance settlements); ‘Rental income of persons’ is the net income
to individuals from renting out property, it includes the net income from the
rental of tenant-occupied housing, the imputed net income from the housing
services of owner-occupied housing, and the royalty income of persons from
patents, copyrights, and rights to natural resources, it does not include the
net income from rental of tenant-occupied housing by corporations or by
partnerships and sole proprietors Source: Bureau of Economic Analysis |
|||
3. Data
The data used in this paper come from four main sources: the Bureau of Economic Analysis (BEA), the Federal Housing Finance Agency (FHFA), the US Census Bureau, and Carrillo, Early and Olsen (2014). The data are all collected on a calendar year basis and typically cover the period from the early 1980s to at least 2012. More detailed information is provided in Appendix A.
I examine several measures of housing capital income that are disaggregated by either state or metropolitan statistical area (MSA). The state-level estimates of gross housing capital income are based on the gross operating surplus of the real estate sector. The real estate sector consists of housing and ‘other real estate’, which essentially measures the output of the commercial real estate sector. This implies that trends in the state-level estimates of real estate output will not perfectly capture the national estimates of housing output. However, at the national level, the output of the housing sector makes up more than 80 per cent of the output of the real estate sector, and this share has been fairly constant over time. This suggests that the state-level estimates will mainly capture housing output rather than other types of real estate. Moreover, if the state-level estimates of real estate gross value added are aggregated to the national level and we compare growth rates to the national estimates of gross value added for the housing sector we find a correlation coefficient of 0.85 for the period from 1963 to 2013.
The BEA does not produce state-level estimates of housing depreciation, so it is not possible to construct state-level estimates of net operating surplus for the housing sector – the measure preferred by Piketty (2014) and Rognlie (2015). This could be problematic if depreciation rates vary over time and differ across states in a systematic way. The American Housing Survey suggests that the age of the housing stock can vary a lot across states – the ‘Sand States’ (e.g. Nevada and Arizona) tend to have much newer housing stock than states in the north-east (e.g. New York). However, this variation in the age of the housing stock has been fairly constant over time. As will be shown, any confounding time-invariant variation in depreciation rates are dealt with in the statistical analysis. Moreover, at the national level, the trend in the share of housing gross value added closely follows that of housing net operating surplus, suggesting that similar relationships hold at more disaggregated levels of geography.
I also collect state-level estimates of net housing profits (or the ‘rental income of persons’) for both owner-occupied and tenant-occupied property. These data are provided by the BEA as part of the State Personal Income accounts.
For the econometric analysis, I augment these data with information on housing prices by state which are available as part of the FHFA Housing Price Index (HPI).[4] The HPI is based on transactions for single-family properties that involve conforming conventional mortgages purchased or securitised by the Government-sponsored enterprises (Fannie Mae or Freddie Mac).[5] The HPI is a weighted index with the weights based on the shares of one-unit detached properties in each state. The HPI is a repeat-sales index so it measures average price changes based on repeat sales or refinancing of the same properties. In effect, the price index abstracts from changes in the composition of housing sold.[6]
To examine relative trends in rents and housing prices, I also utilise a source of state-level information on rents and non-housing prices. I obtain state-level price indices for rents and for all other goods and services from Carrillo et al (2014). The ability to track the prices of all goods and services in each state allows me to construct state-specific relative price estimates for both housing prices and rents. The state-level price indices are produced by first creating cross-sectional price indices for the year 2000 for around 400 metro areas and then using time-series price indices provided by the Bureau of Labor Statistics (BLS) to create a panel of prices. More detailed information on the construction of the price indices can be found at Edgar Olsen's website (<http://eoolsen.weebly.com/price-indices.html>).
I supplement these data with disaggregated information on mortgage lending rates, housing supply elasticities and real GDP growth.
The state-level estimates of mortgage interest rates are obtained from the FHFA. Based on a sample of mortgage lenders, the FHFA obtains information on the terms and conditions of all single-family (non-farm) mortgages that lenders close during the last five business days of each month. The survey includes conventional mortgages. It excludes multi-family loans and refinanced mortgages.
To assess how the elasticity of housing supply varies across states I use the index developed by Saiz (2010). This index is based on the coefficients estimated from a regression of housing price growth on measures of regulatory and physical constraints, as well as pre-determined population levels. The regression is estimated at the MSA level. The measure of regulatory constraints is based on the Wharton Residential Urban Land Use Regulatory Index (Gyourko, Saiz and Summers 2008). The measure of physical constraints compiles information on local geographic characteristics to capture the amount of developable land in a given area. More specifically, Saiz uses satellite-generated data on water bodies, land elevation, and slope steepness at the MSA level to compile an index of land constructability for each metropolitan area that has at least 500,000 inhabitants. Where necessary, I aggregate the ‘elasticity index’ to the state level by weighting the MSA-level indices within a given state (where the weights are given by the amount of land in each state accounted for by each MSA).
Table 2 summaries the state-level estimates of some of the key variables used in the paper. The correlations between some of the key variables are summarised in Appendix B.
| Obs | Mean | Median | Std dev | Min | Max | |
|---|---|---|---|---|---|---|
| Housing gross value added (% of GDP) | 1,784 | 10.2 | 9.9 | 2.4 | 4.2 | 18.6 |
| Net owner-occupied housing income (% of GDP) | 1,784 | 0.7 | 0.7 | 0.7 | −0.5 | 35.6 |
| Net tenant-occupied housing income (% of GDP) | 1,784 | 0.7 | 0.6 | 0.3 | 0.0 | 28.7 |
| Population growth (%) | 1,784 | 1.0 | 0.8 | 1.1 | −6.2 | 8.3 |
| Personal income growth (%) | 1,784 | 6.1 | 5.9 | 3.4 | −9.5 | 27.0 |
| Real GDP growth (%) | 1,784 | 2.6 | 2.6 | 3.1 | −17.9 | 17.8 |
| Nominal mortgage interest rate (%) | 1,784 | 8.2 | 7.7 | 2.7 | 3.5 | 17.1 |
| Real mortgage interest rate (%) | 1,784 | 4.3 | 4.4 | 2.5 | −3.6 | 12.8 |
| CPI inflation (%) | 1,784 | 3.8 | 3.1 | 2.9 | −1.5 | 13.3 |
| Housing supply elasticity (index) | 1,714 | 2.4 | 2.1 | 1.0 | 0.9 | 4.5 |
| Rent to housing prices (index) | 1,478 | 100.7 | 100.2 | 12.5 | 79.3 | 137.0 |
| Relative housing prices (index) | 1,784 | 10.8 | 10.6 | 2.7 | 4.6 | 19.3 |
|
Notes: All estimates are at the state level; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; the elasticity index is not available for two states – Alaska and Hawaii Sources: Bureau of Economic Analysis; Carrillo et al (2014); Federal Housing Finance Agency; Saiz (2010) |
||||||
4. Stylised Facts
4.1 Housing Expenditure and Income by the Type of Housing
If we dig into the national accounts and divide the share of capital income by the type of housing, we find that the secular rise is mainly due to the rising share of income going to owner-occupiers (i.e. imputed rent). The owner-occupier share of aggregate income has risen from just under 2 per cent in 1950 to close to 5 per cent in 2014. The share of income going to landlords (i.e. market rent) has also doubled in the post-war era (left-hand panel of Figure 2). But, in aggregate, the effect of imputed rent is larger simply because there are nearly twice as many home owners as renters in the US economy. A similar, and perhaps even more striking, phenomena is observed in the personal consumption expenditure data (right-hand panel of Figure 2).
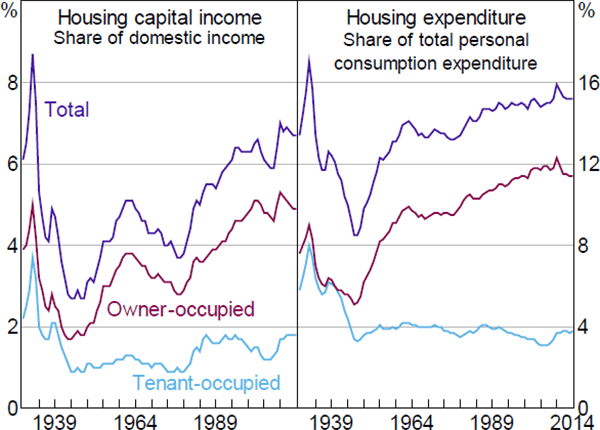
Note: Housing capital income measured as the net operating surplus of the housing sector
Source: Bureau of Economic Analysis
Piketty's first ‘fundamental law of capitalism’ provides a useful framework for decomposing the secular rise in the housing share. In the context of housing, the ‘law’ states that the share of housing capital (or rental) income (α) is equal to: i) the ‘rate of return’ on housing (r) multiplied by ii) the housing wealth-to-income ratio (β). For each type of housing j∈(O,T) (owner-occupied (j = O) or tenant-occupied (j = T)) this can be written as:
where, for each type of housing, total rental income is given by the average rental price (PR) multiplied by the real flow of housing services (YR). The total value of each type of housing stock is given by the average housing price (PH) multiplied by the real stock of housing (KH). For the aggregate economy, total income is given by the average price of all goods and services (P) multiplied by the real flow of all goods and services (Y).
This decomposition in the national accounts suggests that the rise in the share of housing reflects a combination of both a higher rate of return (left-hand panel in Figure 3) and a higher wealth-to-income ratio (right-hand panel in Figure 3). The increase in the rate of return appears to explain the rise in the share of housing capital income in the early 1980s while the rise in the housing wealth-to-income ratio has been the more important factor since the 1990s.
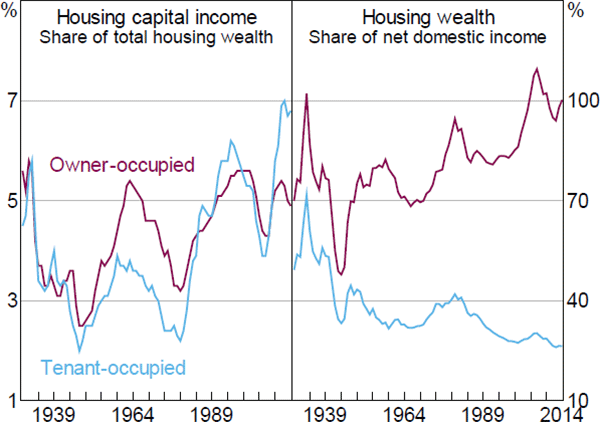
Note: Housing capital income measured as the net operating surplus of the housing sector
Sources: Author's calculations; Bureau of Economic Analysis
But, most strikingly, the decomposition by type of housing indicates that the upward trend in the aggregate housing capital income share is due to an increase in the wealth-to-income ratio for owner-occupied housing. In contrast, the wealth-to-income ratio for tenant-occupied housing has been in steady decline since at least the Great Depression.
An alternative way to decompose the share of housing capital income is to divide it into relative prices and volumes. The national accounts estimates indicate that the aggregate rise in the share of housing in recent decades is solely due to an increase in the price of rents relative to the price of all goods and services (Figure 4). The real share of housing income has been constant since at least the 1960s.
Since 1980, measured on a net value added basis and in nominal terms, the housing share of the economy has risen by more than 2 percentage points. But, measured in real terms, the housing share of the economy has declined slightly over the same period. In other words, the rise in the price of rent (relative to non-housing prices) explains more than 100 per cent of the rise in the housing share of the economy over the past quarter of a century.
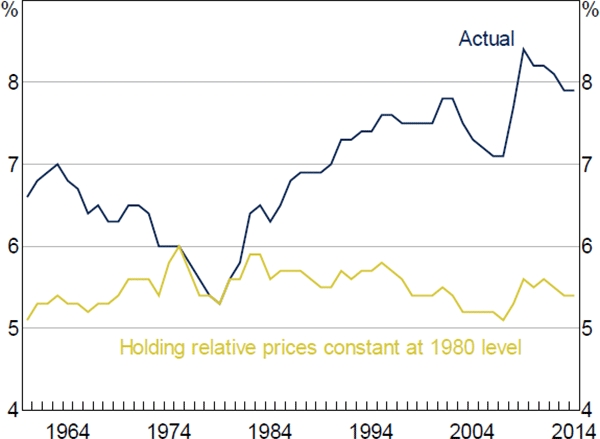
Note: Housing capital income measured as the net value added of the housing sector
Sources: Author's calculations; Bureau of Economic Analysis
It is also possible to look at the prices and volumes of different types of housing in the United States.[7] The national accounts indicate that, over the past 25 years, in nominal terms, the share of aggregate income going to owner-occupiers has risen by 1.9 percentage points and by 0.6 percentage points for landlords. In real terms, the share of aggregate income going to owner-occupiers has been unchanged since 1980 and it has actually fallen by 0.2 percentage points for landlords.
The different real trends for owner-occupied and tenant-occupied housing suggest that factors such as an increase in the rate of home ownership and in the average quality of owner-occupied housing have played some role in explaining the secular rise of housing in recent decades. These differences are reflected in the national accounts estimates of housing investment – the rate of investment for owner-occupied housing has been at least three times as high as that for tenant-occupied housing over the past quarter of a century (Figure 5).[8]
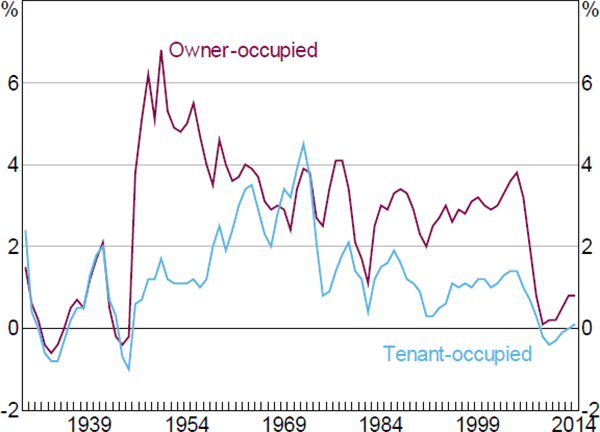
Note: Net housing investment equals gross housing investment less depreciation of the housing stock
Source: Bureau of Economic Analysis
Still, the dominant factor in explaining the secular rise of housing has been the increase in
the price of housing relative to non-housing prices, holding the quality of housing constant
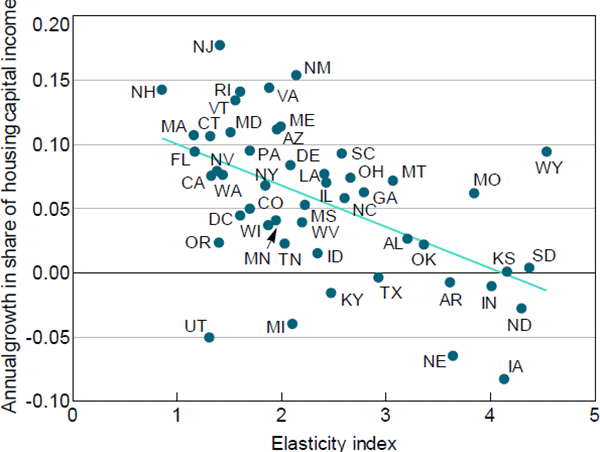
over time. To gain further insight, it is useful to re-write the housing capital share as
consisting of three separate terms: 1) the housing rent-to-price ratio (or ‘user cost of
capital’)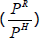 ; 2) the relative price of housing
; 2) the relative price of housing 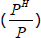 ;
and 3) the relative volume of housing
;
and 3) the relative volume of housing 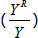 :
:
The housing capital income share can rise as a result of a higher user cost of capital, a higher relative price of housing or a higher relative volume of housing. These three factors are not independent of each other (Poterba 1998). For example, theory suggests that the observed long-run decline in interest rates in recent decades should have lowered the price of renting relative to owning (i.e. the user cost of housing capital should have declined). And the direct effect of this should have been a lower share of the economy going to housing, all other things being equal.
But the indirect effect of the long-run decline in interest rates has been to increase the price of owner-occupied housing (relative to non-housing prices) through higher housing demand. This has increased the nominal share of income going to housing under the assumption that: the relative volume of housing has not declined much in response to the higher relative price because there are few substitutes for housing (i.e. housing demand is price inelastic); and/or new housing production has not responded much due to constraints on the amount of available land (i.e. housing supply is price inelastic).
In a purely accounting sense, a rise in housing prices has no direct impact on the share of capital income in total income (Bonnet et al 2014). But changes in housing prices can have an indirect effect through their impact on rents. To the extent that the housing rent-to-price ratio is stationary over the medium to long-run, higher relative housing prices should translate into higher rental prices (relative to non-housing prices). There is evidence to suggest that rents positively co-move with housing prices (e.g. Davis, Lehnert and Martin 2008; Sommer et al 2013) even if rents are sluggish and move less than one-for-one in response to housing price shocks (e.g. Genesove 2003).
This is what is observed in the data. Over the long-run, there has been a clear rise in the relative price of housing, which has contributed to higher rents relative to non-housing prices (Figure 6). In contrast, the user cost of capital (rents relative to housing prices) has been flat to falling in recent decades. I will build on these observations in the statistical analysis.
Note: (a) Deflated by GDP deflator
Source: Bureau of Economic Analysis
4.2 Housing Expenditure and Income by US State
An alternative way to examine the aggregate trends is to decompose the national accounts by state. The state-level estimates suggest that the rise in the share of housing has been fairly broad based, with only 10 states experiencing outright declines since 1980. These states include: Iowa, Nebraska, Utah, Michigan and North Dakota. In contrast, the states that have experienced the largest increases include: Hawaii, New Jersey, New Mexico, Virginia and New Hampshire.
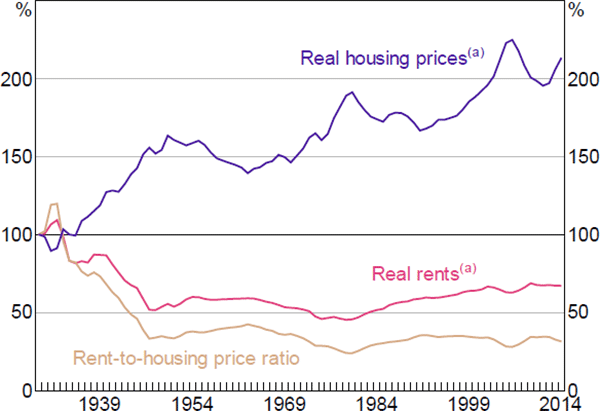
But the most striking feature of the state-level estimates is how the rise in housing capital income has been concentrated in the most supply-inelastic states. The share of housing capital income has generally grown the most along the eastern seaboard (where the supply of housing is typically inelastic) and the least in the midwest (where the supply of housing is more elastic).
To see this clearly, consider Figure 7 in which the states are divided into ‘elastic’ and ‘inelastic’ groups based on whether the Saiz measure of housing supply elasticity is above or below the median.[9] For 50 years, the contribution to total housing capital income of the supply-elastic states has been unchanged at about 3 per cent. In contrast, the contribution of the supply-inelastic states has risen from around 5 per cent in the 1960s to 7 per cent more recently.
Notes: Housing capital income measured as the gross operating surplus of the real estate sector; the analysis abstracts from changes in depreciation
Sources: Author's calculations; Bureau of Economic Analysis; Saiz (2010)
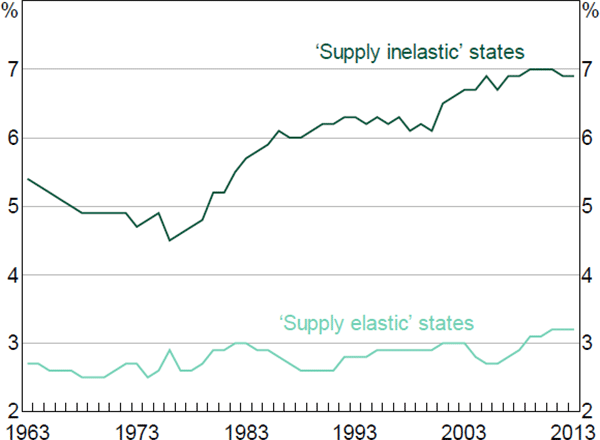
The estimates shown in Figure 7 are based on ‘contributions to growth’ which effectively give more weight to larger states. But the weights are not driving this key result; a similar picture emerges if we exclude large states like California and New York. If we ignore contributions to growth and just compare all the states in terms of the elasticity of housing supply and average (annual) growth in housing income, we observe a clear negative correlation (Figure 8). In other words, the states that are most constrained by housing supply (i.e. those with the lower elasticities) are those that have experienced the fastest growth in housing capital income over recent decades.
Notes: Share of housing capital income measured as housing gross operating surplus divided by GDP at state level; the estimated correlation coefficient shown is −0.52
Sources: Author's calculations; Bureau of Economic Analysis; Saiz (2010)
4.3 The Rise in the Share of Housing Income – Capital or Profit?
In standard long-run growth theory, the way in which capital investment is financed is not important because there are no financial frictions. It does not matter if the growing share of the economy going to housing capital is financed by higher debt or equity because both are equally costly. But financing frictions are pervasive in mortgage markets, even those of advanced economies. For example, potential home buyers typically cannot take out a mortgage equal to the full value of the home in most countries.
It could be argued that if the secular rise in the housing capital share is partly due to a relaxation of borrowing constraints then this has different implications for the distribution of income then if it were financed some other way. The relaxation of the borrowing constraints leads to higher (lifetime) consumption of housing services for owner-occupiers. But at least some of the associated rise in imputed rental income will not ultimately flow to home owners but will instead be absorbed by higher mortgage interest payments. In other words, what matters to the home owner is the net imputed rent (gross imputed rent less mortgage interest payments).
A comparison of the secular trends in net housing capital income and net housing profit income provides a gauge of the relative importance of changes over time in mortgage interest payments.
When measured as net housing capital income (κR − D), the share of the economy going to home owners rose from 3.1 per cent in 1980 to 4.9 per cent in 2014. In contrast, when measured as net housing profit income (πR), the share of the economy going to home owners rose from 0.2 per cent in 1980 to 2.9 per cent in 2014. The larger rise in net housing profit is due to the decline in interest rates over this period. As a result, measured on a net profit basis, the share of the economy going to home owners is currently at its highest level since the Great Depression (Figure 9).
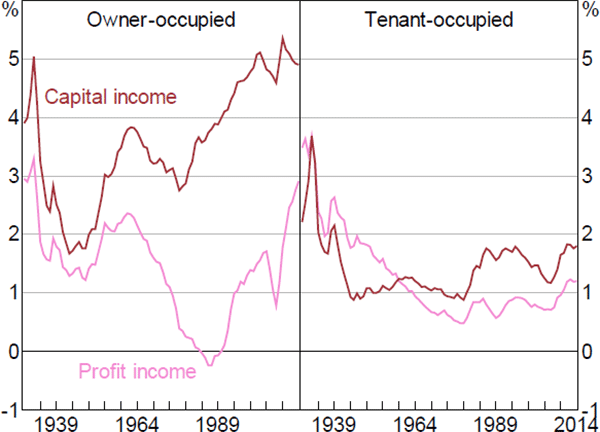
Notes: Housing capital income measured as the net operating surplus of the housing sector; housing profit income measured as the rental income of persons
Source: Bureau of Economic Analysis
This implies that there are at least two channels through which changes in interest rates can affect the distribution of net housing capital income. There is a direct effect as lower interest rates reduce the debt servicing costs of indebted home owners and increase net profits. But there is also an indirect effect as lower interest rates push up land prices (due to an increase in demand for owner-occupied properties). Both channels reinforce each other such that existing home owners will typically take a greater share of aggregate income as interest rates fall.
Overall, the graphical analysis suggests that the story of the secular increase in housing capital income is a story about relative housing prices, interest rates and constraints on the supply of new homes in the United States. I now turn to statistical evidence to further explore these issues.
5. Statistical Evidence
5.1 Housing Income and Mortgage Interest Rates
To explore the determinants of the secular rise in housing capital income, and highlight the key role of the trend decline in interest rates, I estimate a state-level panel regression model. The specification of the model is motivated by the housing user cost of capital literature (Poterba 1984; Díaz and Luengo-Prado 2008). Loosely speaking, the user cost model relates the ratio of rents to housing prices to factors including mortgage interest rates, property taxes, maintenance costs and expected capital gains on housing. More formally:
where the rent-to-housing price ratio 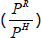 is a function of the nominal mortgage rate (INTRATE), property taxes (T),
maintenance costs (M) and expected housing capital gains (ΔPH).
Note that the user cost formula implies that correlation between mortgage interest rates and the
rent-to-house price ratio is positive. This is because of the underlying arbitrage
condition which implies that a housing investor (including owner-occupiers) should be
indifferent at the margin between purchasing a home (and earning the rental yield) and investing
in alternative assets, such as a bank deposit (and earning the interest rate).[10]
My main focus is on the correlation between mortgage rates and the share of housing capital
income, so I absorb the other terms into a set of control variables and specify a regression
model of the form:
is a function of the nominal mortgage rate (INTRATE), property taxes (T),
maintenance costs (M) and expected housing capital gains (ΔPH).
Note that the user cost formula implies that correlation between mortgage interest rates and the
rent-to-house price ratio is positive. This is because of the underlying arbitrage
condition which implies that a housing investor (including owner-occupiers) should be
indifferent at the margin between purchasing a home (and earning the rental yield) and investing
in alternative assets, such as a bank deposit (and earning the interest rate).[10]
My main focus is on the correlation between mortgage rates and the share of housing capital
income, so I absorb the other terms into a set of control variables and specify a regression
model of the form:
where the dependent variable is housing capital income as a share of total nominal GDP 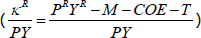 for
state s in t. (Recall that housing capital income at the state level is
proxied using the gross operating surplus of the real estate sector). The key explanatory
variable is the average level of nominal interest rates on new mortgage debt (INTRATE).
The control variables (CONTROLS) include current annual growth in housing prices (as a
proxy for expected capital gains) and average property taxes.
for
state s in t. (Recall that housing capital income at the state level is
proxied using the gross operating surplus of the real estate sector). The key explanatory
variable is the average level of nominal interest rates on new mortgage debt (INTRATE).
The control variables (CONTROLS) include current annual growth in housing prices (as a
proxy for expected capital gains) and average property taxes.
The user cost formula relates specifically to the price of rent, whereas I am interested in
explaining the share of nominal income going to rent 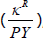 ,
which, as discussed earlier, is a function of the relative price of rent
,
which, as discussed earlier, is a function of the relative price of rent 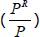 and the relative volume of rent
and the relative volume of rent 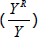 . As such, I also
include demand-side variables that might be expected to influence both the relative price and
relative volume of rent, including population growth and real GDP growth.[11]
. As such, I also
include demand-side variables that might be expected to influence both the relative price and
relative volume of rent, including population growth and real GDP growth.[11]
The specification includes state fixed effects (θs) to control for factors that do not vary with time but potentially determine the proportion of income spent on both market and imputed rent, such as the desirability of the location (e.g. local amenities or distance to the coast).
The model also includes year fixed effects (λt) that control for factors related to the national business cycle (e.g. monetary policy). These fixed effects will absorb all the aggregate time-series variation in each variable, including the net housing capital income share, mortgage interest rates and housing prices. To demonstrate the importance of the time fixed effects I also separately estimate the model with the inclusion of the aggregate federal funds rate (to control for monetary policy) rather than time fixed effects.[12]
I also estimate the same panel regression model but switch the dependent variable from gross housing capital income (as a share of GDP) to net housing profit income (as a share of GDP). This allows for a separate examination of the effect of mortgage interest rates on the income flowing to both owner-occupied and tenant-occupied housing (as the BEA provides these data separately at the state level) as follows:
where I estimate separate regressions for the profits on owner-occupied housing (πOR) and tenant-occupied housing (πTR). All the explanatory variables are as before.
By comparing the estimated effect of mortgage interest rates on housing profit income (πOR) for owner-occupiers and overall housing capital income (κR) we can also gauge the relative importance of the different channels through which interest rates can affect the income flowing to owner-occupiers. Interest rates should have a stronger effect on the net profits of owner-occupiers than on housing capital income. Lower interest rates will boost both net profits and net capital income to the extent that they push up housing prices, but lower interest rates will have an additional effect of increasing net profits by also reducing debt-servicing costs.
The results of estimating Equations (4), (5) and (6) are shown in Table 3. The first three columns show the estimates for housing capital income (κR). The following three columns show the estimates for net housing profits for owner-occupied housing (πOR). The final three columns show the estimates for net housing profits for tenant-occupied housing (πTR).
| Net housing capital income | Net owner-occupied housing profits | Net tenant-occupied housing profits | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |||
| Interest rate | −0.178*** (−6.32) |
−0.082*** (−3.15) |
−0.222* (−1.76) |
−0.203*** (−29.55) |
−0.210*** (−20.19) |
−0.013 (−0.41) |
−0.020*** (−5.90) |
0.015*** (3.78) |
−0.035 (−1.47) |
||
| Housing price growth | −0.030*** (−5.72) |
−0.014* (−1.78) |
−0.003 (−1.15) |
−0.002 (−1.10) |
−0.011*** (−7.85) |
−0.003** (−2.30) |
|||||
| Real GDP growth | −0.052*** (−5.57) |
−0.054*** (−4.64) |
−0.021*** (−6.32) |
−0.007** (−2.41) |
0.001 (0.52) |
−0.005* (−1.84) |
|||||
| Population growth | −0.143*** (−3.07) |
−0.145*** (−2.76) |
−0.016 (−0.53) |
−0.029 (−1.32) |
0.019 (1.29) |
0.011 (0.64) |
|||||
| Federal funds rate | −0.049** (−2.19) |
0.007 (1.23) |
−0.021*** (−8.56) |
||||||||
| State fixed effects | No | Yes | Yes | No | Yes | Yes | No | Yes | Yes | ||
| Year fixed effects | No | No | Yes | No | No | Yes | No | No | Yes | ||
| R2 | 0.055 | 0.272 | 0.339 | 0.605 | 0.647 | 0.927 | 0.033 | 0.230 | 0.611 | ||
| Observations | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | ||
|
Notes: Standard errors are clustered by state; Hausman tests reject the assumption of random state fixed effects; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses |
|||||||||||
The results generally indicate that there is a negative correlation between nominal mortgage interest rates and the share of housing income. A 100 basis point decline in nominal mortgage interest rates is associated with the share of housing capital income rising by between 8 basis points (column 2) and 22 basis points (column 3), on average, depending on the regression specification. The same-sized decline in interest rates is also associated with net profits to home owners rising by between 1.3 basis points (column 6) and 21 basis points (column 5), on average. In contrast, there is some tentative evidence that lower interest rates are associated with lower net profits for landlords (column 8). Recall from Equation (3) that the user cost model points to a positive relationship between interest rates and the rental yield, which is suggestive of the user cost model being more applicable in practice to landlords than to home owners.
Given that interest rates fell, on average, at an annual rate of 17 basis points and the share of housing capital income rose by 7.4 basis points, on average, over the sample period, the results in column 3 suggest that lower nominal interest rates could explain around half the long-run rise in the share of housing capital income (i.e. 0.506 = (−0.17 * −0.222)/0.074).
Perhaps the most striking feature of these results is the fact that the negative correlation between mortgage interest rates and housing capital income generally persists even after controlling for changes in monetary policy through the inclusion of year fixed effects (columns 3, 6 and 9). This is remarkable given that there is limited variation in mortgage interest rates across states, with most of the variation coming from the time series.
If we compare across similar model specifications (e.g. columns 2 and 5 or columns 3 and 6), there is some evidence that the correlation between interest rates and the share of owner-occupier profits is economically larger than the same correlation between interest rates and the share of housing capital income. For example, in the model with the federal funds rate, the coefficient estimate is −0.210 for owner-occupier profits (column 5) and −0.082 for housing capital income (column 2). This provides some evidence that lower interest rates affect net housing income through two channels: through their indirect effect on housing demand (apparent in both models) and their direct effect on debt-servicing costs (only apparent in the owner-occupier profit model).[13]
The coefficient estimate on expected housing capital gains (as proxied by current housing price growth) is, in general, negatively signed, which is consistent with the user cost of capital model. The coefficient estimates on the other control variables are somewhat surprising. In general, we would expect higher GDP and population growth to be associated with higher housing demand, and hence a greater share of the state economy going to the housing sector. But the estimates generally point to the opposite, with both growth in real GDP and the population being negatively correlated with the share of income going to housing.
5.2 Housing Income, Real Interest Rates and Consumer Price Inflation
Next, I estimate a specification in which I decompose the nominal interest rate into two components using the Fisher equation: 1) the real interest rate; and 2) consumer price inflation:[14]
where the key explanatory variables are the average level of real interest rates on new mortgage debt (RINTRATE) and average CPI inflation (ΔCPI). This allows for an examination of the channels through which changes in nominal interest rates might have affected the housing capital income share. In particular, if financial deregulation was important we might expect to observe a negative correlation between real interest rates and the housing capital income share, while if disinflation mattered we should observe a negative correlation between CPI inflation and the share of housing capital income.[15] Again, I estimate separate models for net housing capital income and profits.
The results of estimating Equation (7) are shown in Table 4. The decomposition of nominal interest rates into real interest rates and inflation suggests that both factors are negatively correlated with the share of housing income. This is true even after allowing for monetary policy changes through the inclusion of the federal funds rate (columns 2, 5 and 8). However, the inclusion of time dummies results in the estimated coefficients on both terms generally being outside traditionally accepted levels of statistical significance (columns 3, 6 and 9).
Over the sample period, I estimate that consumer price inflation fell by more than the level of real interest rates, on average. Moreover, the coefficient estimate on inflation is, in general, about the same (or slightly larger) than the coefficient estimate on the real interest rate. Taken together, this provides some evidence that lower inflation is more economically important than lower real interest rates in explaining the secular rise in the share of housing capital income.[16]
| Net housing capital income | Net owner-occupied housing profits | Net tenant-occupied housing profits | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | |||
| Real interest rate | −0.162*** (−5.88) | −0.124*** (−4.36) | −0.226* (−1.72) | −0.215*** (−30.65) | −0.214*** (−18.26) | −0.016 (−0.49) | −0.005 (−1.59) | 0.001 (0.17) | −0.036 (−1.44) | ||
| CPI inflation | −0.199*** (−6.29) | −0.160*** (−4.28) | −0.072 (−0.48) | −0.204*** (−28.22) | −0.197*** (−14.56) | −0.060 (−1.37) | −0.030*** (−8.10) | −0.016*** (−3.06) | −0.027 (−0.96) | ||
| Housing price growth | −0.026*** (−4.47) | −0.020** (−2.35) | −0.003 (−1.33) | −0.001 (−0.41) | −0.010*** (−6.65) | −0.004** (−2.45) | |||||
| Real GDP growth | −0.057*** (−6.24) | −0.054*** (−4.86) | −0.021*** (−6.33) | −0.007** (−2.41) | 0.001 (−0.28) | −0.005* (−1.86) | |||||
| Population growth | −0.137*** (−2.95) | −0.149*** (−2.84) | −0.018 (−0.62) | −0.028 (−1.31) | 0.022 (1.43) | 0.010 (0.63) | |||||
| Federal funds rate | −0.008 (−0.48) | −0.002 (−0.29) | −0.004* (−1.74) | ||||||||
| State fixed effects | No | Yes | Yes | No | Yes | Yes | No | Yes | Yes | ||
| Year fixed effects | No | No | Yes | No | No | Yes | No | No | Yes | ||
| R2 | 0.058 | 0.278 | 0.342 | 0.606 | 0.650 | 0.928 | 0.073 | 0.258 | 0.612 | ||
| Observations | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | 1,784 | ||
|
Notes: Standard errors are clustered by state; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses |
|||||||||||
5.3 Housing Income, Interest Rates and Supply Constraints
If lower interest rates contributed to more income being spent on housing then we would also expect this effect to be particularly strong in states that are constrained in terms of land supply. To test this hypothesis I re-estimate the models and interact each explanatory variable with a dummy variable (INELASTIC) for whether the state is supply-constrained or not:
where all the variables are as before, except the inclusion of the dummy variable INELASTIC which takes the value of one if the state is constrained and is zero otherwise. A state is assumed to be supply-constrained if the Saiz elasticity index is below the median value of 2.1 (measured at the state level). The results of estimating these equations are shown in Table 5.
The results are consistent with the hypothesis that interest rates have a stronger effect on the housing capital income share in supply-constrained areas. In particular, the estimates in column 1 indicate that a 100 basis point decline in nominal interest rates is associated with the housing capital income share rising by about 21.6 basis points in the ‘elastic states’ and by 32.1 basis points in the ‘inelastic states’. Moreover, this difference in the sensitivity of the two types of states is statistically significant. The estimates in column 2 suggest that a 100 basis point decline in real interest rates is associated with a 22.5 basis point rise in the housing capital income share in the elastic states and a 29.4 basis point increase in the inelastic states. This difference is again statistically significant. A fall in inflation of 1 percentage point is associated with a rise in the housing capital income share of 21.8 basis points in the supply-constrained states, on average. In contrast, the effect of disinflation is estimated to be insignificant in the elastic states.
Similar patterns emerge when looking at the effects of interest rates on net profits going to home owners (columns 3 and 4) and to landlords (columns 5 and 6). In general, the negative effect of interest rates is stronger in the supply-constrained states and this negative effect reflects a combination of both real interest rates and inflation.
| Net housing capital income | Net owner-occupied housing profits | Net tenant-occupied housing profits | ||||||
|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | |||
| Interest rate | −0.216* (−1.73) |
0.042* (1.87) |
−0.048*** (−3.82) |
|||||
| INELASTIC × interest rate |
−0.105** (−2.37) |
−0.044*** (−4.19) |
−0.023*** (−4.81) |
|||||
| Real interest rate | −0.225* (−1.77) |
0.042* (1.78) |
−0.049*** (−3.80) |
|||||
| INELASTIC × real interest rate |
−0.069* (−1.74) |
−0.046*** (−4.42) |
−0.022*** (−4.41) |
|||||
| CPI inflation | −0.069 (−0.43) |
0.022 (0.75) |
−0.033** (−2.42) |
|||||
| INELASTIC × CPI inflation |
−0.149*** (−2.69) |
−0.045*** (−3.97) |
−0.026*** (−4.74) |
|||||
| Housing price growth | −0.001 (−0.07) |
−0.021 (−1.06) |
0.001 (0.54) |
0.002 (0.61) |
−0.006 (−1.42) |
−0.007* (−1.79) |
||
| INELASTIC × housing price growth |
−0.022 (−1.26) |
−0.002 (−0.12) |
−0.003 (−0.96) |
−0.002 (−0.77) |
0.002 (0.59) |
0.003 (0.99) |
||
| Real GDP growth | −0.052*** (−3.17) |
−0.051*** (−3.36) |
−0.007* (−1.82) |
−0.007* (−1.75) |
−0.003 (−0.85) |
−0.003 (−0.86) |
||
| INELASTIC × real GDP growth |
0.024 (1.17) |
0.015 (0.73) |
0.008** (2.19) |
0.007** (2.06) |
0.003 (0.72) |
0.002 (0.57) |
||
| Population growth | −0.186** (−2.50) |
−0.182** (−2.46) |
−0.028 (−1.11) |
−0.028 (−1.11) |
0.049 (1.54) |
0.049 (1.54) |
||
| INELASTIC × real GDP growth |
0.140 (1.43) |
0.137 (1.36) |
−0.026 (−0.63) |
−0.024 (−0.58) |
−0.044 (−1.36) |
−0.045 (−1.37) |
||
| State fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | ||
| Time fixed effects | Yes | Yes | Yes | Yes | Yes | Yes | ||
| R2 | 0.367 | 0.376 | 0.942 | 0.943 | 0.662 | 0.663 | ||
| Observations | 1,714 | 1,714 | 1,714 | 1,714 | 1,714 | 1,714 | ||
| Notes: Standard errors are clustered by state; the sample period is that underpinning the regression estimates, which covers the years from 1978 to 2012; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses | ||||||||
6. Conclusion
I provide evidence that the secular increase in housing's share of the US economy reflects a combination of lower interest rates and housing supply constraints. More specifically, by decomposing the national accounts and exploiting variation across states, I provide evidence that the rise in the share of housing capital income in recent decades can be traced to: 1) both disinflation and lower real interest rates (which contributed to an expansion of credit for owner-occupied housing); and 2) constraints on the supply of new housing in some large cities. The evidence I uncover is consistent with the hypothesis that disinflation and financial deregulation acted as aggregate demand shocks to push up the relative price of land in supply-constrained areas, which, in turn, contributed to a higher share of nominal income spent on housing.
The results in this paper relate specifically to the United States, but it would be interesting to examine whether similar stories can be told for other advanced economies, given that the long-run increase in the share of housing capital income has occurred across a range of economies (Rognlie 2015). In particular, future research could examine the determinants of housing capital income by exploiting the cross-country variation in the institutional arrangements within mortgage and rental markets.
The analysis in this paper highlights the important role of housing values in not only the distribution of wealth, but also the distribution of income in the United States. The observed increase in the share of aggregate income going to housing capital might even understate the importance of housing prices to the income distribution. As shown in the introduction of this paper, the non-housing capital income share has been stable for several decades. But, within the non-housing sector, there has been an increase in the share of capital income going to financial corporations (Figure 10). A large share of the income flowing to the financial sector is presumably related to the growth in intermediation services; services which are traditionally dependent on housing collateral, and ultimately land prices.
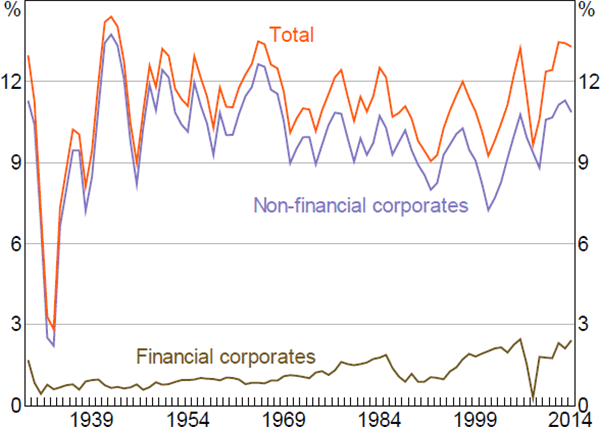
Source: Bureau of Economic Analysis
My results also potentially speak to a new literature on the distributional effects of monetary policy. This literature is still in its infancy, but it is surprising how little research there has been on the link between monetary policy and inequality via the housing sector. As is well known, for most advanced economies, housing typically makes up the largest share of total wealth for most households. Moreover, imputed rent for owner-occupiers often makes up the largest share of total household spending in the national accounts. The link between monetary policy and inequality via housing prices and imputed rent should be a fruitful area of future research.
Appendix A: Sources of Data
| Series | Notes | Sample period | Unit | Source |
|---|---|---|---|---|
| Housing prices | Index based on repeat sales of single-family properties that have mortgages which have been purchased or securitised by Fannie Mae or Freddie Mac | 1975–2014 | MSA | FHFA |
| Mortgage interest rates | Average interest rate on new conventional single-family mortgages | 1978–2012 | State | FHFA |
| Total personal income | Compensation of employees plus self-employment income plus rental income of persons plus asset income plus current transfer receipts less contributions for government social insurance | 1958–2014 | MSA | BEA |
| Population | Number of resident individuals | 1980–2014 | MSA | Census Bureau |
| Housing sector gross value added | Total space rent (both imputed and not imputed) on the housing stock less maintenance costs | 1963–2014 | State | BEA |
| Rental income of persons – owner-occupier | Net operating surplus to owner-occupiers (i.e. gross imputed rent less housing expenses for owner-occupiers) | 1958–2014 | State | BEA |
| Rental income of persons – tenant-occupier | Net operating surplus to private landlords (i.e gross rent less housing expenses) | 1958–2014 | State | BEA |
| Gross domestic product (GDP) | Personal income plus gross operating surplus plus taxes on production and imports less government transfers | 1963–2014 | State | BEA |
| Consumer price index (CPI) | The CPI indices constructed for each state for the year 2000 based on price information provided by the American Chambers of Commerce Researchers Association combined with average expenditure shares from the Consumer Expenditure Survey; time-series price indices from the Bureau of Labor Statistics are used to create a panel of price indices | 1982–2010 | State | Carrillo et al (2014) |
Appendix B: Variable Correlations
The correlations between the key variables are summarised in Table B1.
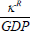 |
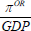 |
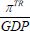 |
Interest rate | Real interest rate | ΔCPI | ΔHP | ΔGDP | ΔPop | |
|---|---|---|---|---|---|---|---|---|---|
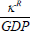 |
1.00 | ||||||||
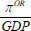 |
0.38 | 1.00 | |||||||
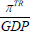 |
0.27 | 0.32 | 1.00 | ||||||
| Interest rate | −0.23 | −0.78 | −0.18 | 1.00 | |||||
| Real interest rate | −0.05 | −0.32 | 0.11 | 0.40 | 1.00 | ||||
| ΔCPI | −0.17 | −0.43 | −0.27 | 0.56 | −0.54 | 1.00 | |||
| ΔHP | −0.17 | −0.25 | −0.25 | 0.24 | −0.19 | 0.39 | 1.00 | ||
| ΔGDP | −0.07 | −0.11 | −0.04 | 0.03 | −0.06 | 0.08 | 0.43 | 1.00 | |
| ΔPop | 0.12 | −0.01 | −0.02 | 0.02 | −0.07 | 0.08 | 0.24 | 0.32 | 1.00 |
|
Sources: Bureau of Economic Analysis; Carrillo et al (2014); Federal Housing Finance Agency |
|||||||||
Appendix C: Banking Deregulation and Housing Capital Income
In this appendix, I look for more direct evidence that the deregulation of the US banking sector contributed to the rise in housing capital income by boosting the supply of mortgage credit and, in turn, the demand for owner-occupied housing. Before doing so, it is helpful to briefly outline the institutional background to US banking deregulation.
The US banking sector has undergone significant reform in recent decades (Kroszner and Strahan 1999; Sherman 2009). During the last quarter of the twentieth century, federal and state authorities removed geographic restrictions on: 1) intrastate bank branching (i.e. establishing branches within a state); 2) interstate banking (i.e. establishing subsidiary banks across states); and 3) interstate branching (i.e. establishing branches across states) (Jiang, Levine and Lin 2014).
This culminated in the passage of the Riegle-Neal Interstate Banking and Branching Efficiency Act in 1994. After this time, both national and state-chartered banks were allowed to operate and open branches across state borders without formal authorisation from the state authorities. However, states retained the right to impose restrictions on the extent of geographic expansion. For instance, states were allowed to place limits on the size of banks or forbid ‘de novo branching’ (i.e. the establishment of new branches).
Rice and Strahan (2010) construct an index to capture the differences in restrictions on interstate branching across states and over time. The regulation index runs from 1994 to 2005 and takes values between 0 and 4. The value of the index depends on the number of different branching restrictions in place at a point in time (up to a maximum of four restrictions). For my purposes I ignore the number of restrictions and simply construct a ‘deregulation index’ that takes the value of 1 if at least one restriction has been removed and is 0 otherwise. In effect, I assume that every state is fully restricted in 1994 (i.e. the index equals 0) and is fully unrestricted as soon as at least one restriction is removed (i.e. the index equals 1).[17] As will be discussed, I do this to aid the interpretation of the results in a difference-in-difference modelling framework. My key results are not affected by ignoring the additional information contained in the number of state-level restrictions. I also extend the series beyond 2005 by keeping the value of the index for each state constant at its 2005 level.
To identify the effect of financial liberalisation on housing capital income I exploit variation over states and time in exogenous restrictions on interstate bank branching. My identification strategy is based on an experimental research design that has been used extensively in the banking and housing economics literature (e.g. Jayaratne and Strahan 1996; Black and Strahan 2002; Kerr and Nanda 2009; Rice and Strahan 2010; Michalski and Ors 2012; Krishnamurthy 2013; Berger et al 2015). My strategy most closely follows the method outlined in Favara and Imbs (2015). Consider the following panel regression:
where the dependent variable is the relative price of owner-occupied housing for metropolitan statistical area m in state s in year t. The explanatory variables include a dummy variable (INELASTIC) for whether the metro area is above its state median in terms of being inelastic in housing supply. This is interacted with a dummy variable for whether the state has deregulated or not in a particular year (DEREG). The deregulation index equals 1 as soon as the state deregulates (and stays equal to 1 thereafter). Note that the (in)elasticity index varies by metro area while the deregulation index varies across states and over time.
Note also that I focus on relative prices in the regression because the preceding analysis suggested that the long-run rise in the share of housing capital is due to relative prices. Furthermore, the data on housing capital income at the MSA level is of relatively poor quality.[18]
The staggered pace of reform across states provides important variation in the timing (and size) of the credit supply shock. But it also raises the question of what caused this variation. It could be argued that the removal of restrictions on interstate branching was endogenous to local housing market conditions (i.e. E(DEREGst * εmst)≠0). For example, state policymakers may have been more open to entry by out-of-state banks if conditions in their housing market were particularly weak. Any subsequent increase in housing demand (and relative prices) may just reflect a return to more normal conditions, rather than the adoption of the law. However, Kroszner and Strahan (1999) provide evidence that the bank branching restrictions were correlated with the lobbying power of small banks, and not with contemporaneous economic conditions. (States were less likely to deregulate when the small banks held significant market share as they were less inclined than large banks to expand across state borders.)
Regardless, I circumvent this problem by exploiting variation in housing supply elasticity within a state at a given point in time. More specifically, I include linear state-specific time trends (λst) in the regression model. These trends absorb any linear changes in relative housing prices across states and, more importantly, may also capture latent factors that influenced state policymakers to remove the branching restrictions at a particular point in time. The assumption underlying this strategy is that the decision to change state laws may be associated with average conditions in the state but is unlikely to be correlated with conditions between metro areas within a state.
The timing of deregulation may also be correlated with the supply elasticity of the local housing market. For example, expansion-minded large banks may have been more inclined to push for deregulation in areas that are particularly constrained by supply in order to capture the rents associated with any increase in housing demand. But this would just imply a negative correlation between the level of the deregulation index and the elasticity of housing supply and should not bias the coefficient estimates. Moreover, I find that the main results hold even after excluding the largest capital cities, such as Chicago, Los Angeles and New York, where this problem is likely to be most acute.
There may also be serial correlation in the relative price of housing and in the deregulation indicator (which is essentially a state-specific time series of zeroes and ones). To deal with this serial correlation and estimate conservative standard errors, I follow the recommendation of Bertrand, Duflo and Mullainathan (2004) and collapse the model to two periods – ‘before’ and ‘after’ deregulation. I do this by taking the unweighted average of each variable in the pre- and post-deregulation periods. I then take the difference between these two periods to arrive at the final specification to be estimated:[19]
where I have removed the time subscript to highlight the fact that it is a cross-sectional regression with one observation per metro area in the sample. This is essentially a difference-in-differences model. The causal effect of credit supply on the relative price of housing is identified by the difference in relative housing price growth between inelastic metro areas (the treatment group) and elastic metro areas (the control group) within the same state following the removal of the branching restrictions (the treatment).
A positive coefficient on the inelasticity indicator (β) indicates that the relative price of housing rose by more in the inelastic metro areas than in the elastic metro areas of the same state following deregulation. This would be consistent with the hypothesis that the credit supply shock had a relatively large impact on real housing prices in metro areas with more restricted housing supply.
There are a few differences between my identification strategy and that followed by Favara and Imbs (2015). First, I allow for state-specific time trends in the specification and hence exploit variation between metro areas within the same state at a given point in time. They instead exploit variation between a treated group of banks and a placebo sample of non-bank mortgage lenders that were not affected by the change in bank branching laws. Second, I focus on the determinants of growth in relative housing prices rather than housing price growth per se. I therefore allow for the possibility that a rise in housing prices might reflect a more general increase in prices in the local area. It is important to control for non-housing prices as housing and non-housing prices tend to positively co-move across cities (Albouy et al 2014); cities where housing is expensive are cities where non-housing services (e.g. restaurant meals, haircuts, dry cleaning) are also expensive. Third, to control for serial correlation, I collapse the data to two periods while they estimate models with lagged dependent variables on the full sample of annual observations.
To test the causal effect of financial deregulation on the relative price of housing I first look for graphical evidence that the common (or parallel) trends assumption is satisfied (Angrist and Pischke 2009). The trends in the relative price of housing for the inelastic and elastic metro areas are plotted in Figure C1. The series are both indexed to 100 in the year in which deregulation occurred. The graphical evidence is consistent with the hypothesis that housing prices increased (relative to non-housing prices) at the time of deregulation and that this effect was much stronger in the metro areas in which housing is inelastically supplied.
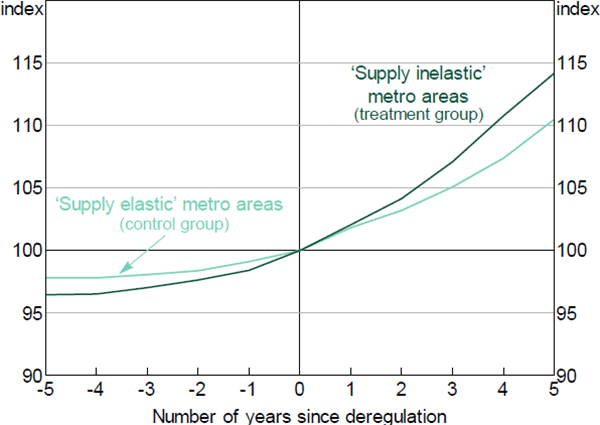
Sources: Author's calculations; Carrillo et al (2014); Federal Housing Finance Agency
Next I turn to the statistical evidence. The results of estimating Equation (C1) are shown in Table C1. I show estimates with and without state fixed effects and with and without controls.
The basic OLS estimates (column 1) point to an average treatment effect (ATE) of around 4 per cent. In other words, the relative price of housing increased by 4 per cent in the inelastic metro areas relative to the elastic metro areas, on average, after deregulation. The inclusion of control variables (column 2) – namely, population growth and real personal (per capita) income growth – reduces the economic significance of the estimated ATE but it remains statistically significant at the 1 per cent level. As might be expected, (per capita) personal income growth is positively correlated with a higher relative price of housing. Population growth appears to have an insignificant effect, at least in the fixed effects specifications.
The preferred within-state estimates indicate that the relative price of housing rises by 2.7 per cent, on average, in the inelastic metro areas relative to the elastic metro areas following deregulation (column 3). Similar results obtain if I replace the dummy for inelastic metro areas with a continuous variable for the extent of elasticity. In a sense, this variable measures the ‘intensity of treatment’ – the more elastic is the housing stock the less effect the credit supply shock should have on relative housing prices. And I find that in metro areas in which the supply of housing is particularly inelastic, the effect of deregulation on housing prices is stronger (column 4).
| OLS | Fixed effects | ||||
|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | ||
| Inelastic supply dummy | 0.040*** (4.04) |
0.030*** (3.05) |
0.028*** (3.01) |
||
| Inelastic supply indicator | 0.010* (1.72) |
||||
| Population growth | 0.177*** (2.90) |
0.003 (0.07) |
−0.008 (−0.19) |
||
| Real personal income growth | 0.383*** (3.05) |
0.502*** (5.45) |
0.515*** (5.30) |
||
| Constant | 0.126*** (9.13) |
0.026 (0.85) |
0.030 (1.41) |
0.070** (2.65) |
|
| State fixed effects | No | No | Yes | Yes | |
| R2 | 0.046 | 0.174 | 0.707 | 0.698 | |
| Observations | 276 | 276 | 276 | 276 | |
|
Notes: Standard errors are clustered by state; ***, **, and * denote significance at the 1, 5 and 10 per cent level, respectively; t statistics in parentheses |
|||||
In terms of economic significance, if the elasticity index were increased from the 25th percentile to the 75th percentile, the relative price of housing would rise by 1.7 percentage points less in response to the credit supply shock than otherwise. In a rough sense, this would be equivalent to converting the amount of developable land from an ‘inelastic’ city like Denver, Colorado to a more elastic city like Kansas City, Missouri.
Overall, the results are consistent with the hypothesis that the removal of interstate bank branching constraints had a relatively large effect on prices in the metro areas in which the supply of housing is inelastic. This is expected if supply constraints matter, namely that better access to credit will feed through to house prices more in regions where the supply of houses cannot adjust as easily.[20]
References
Albouy D, G Ehrlich and Y Liu (2014), ‘Housing Demand and Expenditures: How Rising Rent Levels Affect Behavior and Cost-Of-Living over Space and Time’, Paper presented at CEP/LSE Labour Seminar, London, 28 November.
Angrist JD and J-S Pischke (2009), Mostly Harmless Econometrics: An Empiricist's Companion, Princeton University Press, Princeton.
Berger EA, AW Butler, E Hu and M Zekhnini (2015), ‘Credit Be Dammed: The Impact of Banking Deregulation on Economic Growth’, Unpublished manuscript, Jones Graduate School of Business, Rice University, August.
Bertrand M, E Duflo and S Mullainathan (2004), ‘How Much Should We Trust Differences-In-Differences Estimates?’, The Quarterly Journal of Economics, 119(1), pp 249–275.
Black SE and PE Strahan (2002), ‘Entrepreneurship and Bank Credit Availability’, The Journal of Finance, 57(6), pp 2807–2833.
Bonnet O, P-H Bono, G Chapelle and E Wasmer (2014), ‘Does Housing Capital Contribute to Inequality? A Comment on Thomas Piketty's Capital in the 21st Century’, Sciences Po Economics Discussion Paper No 2014-07.
Borri N and P Reichlin (2015), ‘The Housing Cost Disease’, Centre for Economic Policy Research Discussion Paper Series No 10756.
Carrillo PE, DW Early and EO Olsen (2014), ‘A Panel of Interarea Price Indices for All Areas in the United States 1982–2012’, Journal of Housing Economics, 26, pp 81–93.
Davis MA, A Lehnert and RF Martin (2008), ‘The Rent-Price Ratio for the Aggregate Stock of Owner-Occupied Housing’, The Review of Income and Wealth, 54(2), pp 279–284.
Davis MA and F Ortalo-Magné (2011), ‘Household Expenditures, Wages, Rents’, Review of Economic Dynamics, 14(2), pp 248–261.
Díaz A and MJ Luengo-Prado (2008), ‘On the User Cost and Homeownership’, Review of Economic Dynamics, 11(3), pp 584–613.
Diewert E (2003), ‘The Treatment of Owner Occupied Housing and Other Durables in a Consumer Price Index’, University of British Columbia Discussion Paper No 03-08.
Duca JV, J Muellbauer and A Murphy (2011), ‘House Prices and Credit Constraints: Making Sense of the US Experience’, The Economic Journal, 121(552), pp 533–551.
Economist, The (2015), ‘The Paradox of Soil’, The Economist, 4–10 April, pp 18–20.
Ellis L (2005), ‘Disinflation and the Dynamics of Mortgage Debt’, Investigating the Relationship between the Financial and Real Economy, BIS Papers No 22, Bank for International Settlements, Basel, pp 5–20.
Ellis L (2006), ‘Housing and Housing Finance: The View from Australia and Beyond’, RBA Research Discussion Paper No 2006-12.
Ellis L and K Smith (2010), ‘The Global Upward Trend in the Profit Share’, Applied Economics Quarterly, 56(3), pp 231–255.
Elsby MWL, B Hobijn and A Şahin (2013), ‘The Decline of the U.S. Labor Share’, Brookings Papers on Economic Activity, 47(Fall), pp 1–52.
Favara G and J Imbs (2015), ‘Credit Supply and the Price of Housing’, The American Economic Review, 105(3), pp 958–992.
Favilukis J, SC Ludvigson and S Van Nieuwerburgh (2010), ‘The Macroeconomic Effects of Housing Wealth, Housing Finance, and Limited Risk-Sharing in General Equilibrium’, NBER Working Paper No 15988, rev February 2015.
Frank RH (2005), ‘Positional Externalities Cause Large and Preventable Welfare Losses’, The American Economic Review, 95(2), pp 137–141.
Gallin J (2003), ‘The Long-Run Relationship between House Prices and Income: Evidence from Local Housing Markets’, Board of Governors of the Federal Reserve System Finance and Economics Discussion Series No 2003-17.
Garner TI and R Verbrugge (2009), ‘Reconciling User Costs and Rental Equivalence: Evidence from the U.S. Consumer Expenditure Survey’, Bureau of Labor Statistics Working Paper No 427.
Genesove D (2003), ‘The Nominal Rigidity of Apartment Rents’, The Review of Economics and Statistics, 85(4), pp 844–853.
Guscina A (2006), ‘Effects of Globalization on Labor's Share in National Income’, IMF Working Paper No WP/06/294.
Gyourko J, C Mayer and T Sinai (2013), ‘Superstar Cities’, American Economic Journal: Economic Policy, 5(4), pp 167–199.
Gyourko J, A Saiz and A Summers (2008), ‘A New Measure of the Local Regulatory Environment for Housing Markets: The Wharton Residential Land Use Regulatory Index’, Urban Studies, 45(3), pp 693–729.
Hilber CAL and W Vermeulen (2016), ‘The Impact of Supply Constraints on House Prices in England’, The Economic Journal, 126(591), pp 358–405.
Jayaratne J and PE Strahan (1996), ‘The Finance-Growth Nexus: Evidence from Bank Branch Deregulation’, The Quarterly Journal of Economics, 111(3), pp 639–670.
Jiang L, R Levine and C Lin (2014), ‘Competition and Bank Opacity’, NBER Working Paper No 20760.
Karabarbounis L and B Neiman (2014), ‘The Global Decline of the Labor Share’, The Quarterly Journal of Economics, 129(1), pp 61–103.
Kerr WR and R Nanda (2009), ‘Democratizing Entry: Banking Deregulations, Financing Constraints, and Entrepreneurship’, Journal of Financial Economics, 94(1), pp 124–149.
Krishnamurthy P (2013), ‘Banking Deregulation, Local Credit Supply, and Small Business Growth’, Unpublished manuscript, University of California, Berkeley, August.
Kroszner RS and PE Strahan (1999), ‘What Drives Deregulation? Economics and Politics of the Relaxation of Bank Branching Restrictions’, The Quarterly Journal of Economics, 114(4), pp 1437–1467.
Mayerhauser N and M Reinsdorf (2007), ‘Housing Services in the National Economic Accounts’, Bureau of Economic Analysis Methodology Paper, September.
McCarthy J, RW Peach and MS Ploenzke (2010), ‘The Measurement of Rent Inflation’, Federal Reserve Bank of New York Staff Report No 425, rev August 2015.
Michalski T and E Ors (2012), ‘(Interstate) Banking and (Interstate) Trade: Does Real Integration Follow Financial Integration?’, Journal of Financial Economics, 104(1), pp 89–117.
Piketty T (2014), Capital in the Twenty-First Century, trans A Goldhammer, The Belknap Press of Harvard University Press, Cambridge.
Piketty T (2016), ‘Capital, Predistribution and Redistribution’, Crooked Timber blog, 4 January, viewed 6 January 2016.
Piketty T and G Zucman (2014), ‘Capital is Back: Wealth-Income Ratios in Rich Countries 1700–2010’, The Quarterly Journal of Economics, 129(3), pp 1255–1310.
Poterba JM (1984), ‘Tax Subsidies to Owner-Occupied Housing: An Asset-Market Approach’, The Quarterly Journal of Economics, 99(4), pp 729–752.
Poterba JM (1998), ‘The Rate of Return to Corporate Capital and Factor Shares: New Estimates Using Revised National Income Accounts and Capital Stock Data’, Carnegie-Rochester Conference Series on Public Policy, 48, pp 211–246.
Rice T and PE Strahan (2010), ‘Does Credit Competition Affect Small-Firm Finance?’, The Journal of Finance, 65(3), pp 861–889.
Rognlie M (2015), ‘Deciphering the Fall and Rise in the Net Capital Share: Accumulation or Scarcity?’, Brookings Papers on Economic Activity, Spring, pp 1–54.
Saiz A (2010), ‘The Geographic Determinants of Housing Supply’, The Quarterly Journal of Economics, 125(3), pp 1253–1296.
Sherman M (2009), ‘A Short History of Financial Deregulation in the United States’, Center for Economic and Policy Research Report, July.
Short K, A O'Hara and S Susin (2007), ‘Taking Account of Housing in Measures of Household Income’, U.S. Census Bureau, Social, Economic, and Housing Statistics Division Working Paper 2007-02.
Smith N (2015), ‘The Threat Coming by Land’, Bloomberg View, 9 September, viewed October 2015.
Sommer K, P Sullivan and R Verbrugge (2013), ‘The Equilibrium Effect of Fundamentals on House Prices and Rents’, Journal of Monetary Economics, 60(7), pp 854–870.
Stiglitz JE (2015), ‘New Theoretical Perspectives on the Distribution of Income and Wealth among Individuals: Part IV: Land and Credit’, NBER Working Paper No 21192.
Weil DN (2015), ‘Capital and Wealth in the Twenty-First Century’, The American Economic Review, 105(5), pp 34–37.
Acknowledgements
The author is grateful to John Barrdear, Luci Ellis, Angus Foulis, Leonardo Gambacorta, Greg Kaplan, Jonathan Kearns, Michael Kumhof, Matthew Read, Hyun Song Shin, Silvana Tenreyro and Peter Tulip for helpful advice, comments and suggestions. The author completed this project while visiting the Bank for International Settlements under the Central Bank Research Fellowship program.
Footnotes
The flipside of this has been a decline in the labour share of the economy (e.g. Guscina 2006; Ellis and Smith 2010; Elsby, Hobijn and Şahin 2013; Karabarbounis and Neiman 2014). [1]
Borri and Reichlin (2015) suggest an alternative explanation for the secular rise of housing. Based on a two-sector, life-cycle model, they suggest that if productivity in the manufacturing sector grows more rapidly than that in the housing construction sector, then this will lead to a higher relative price for housing services in equilibrium. And if housing demand is sufficiently price inelastic, this in turn will contribute to a higher nominal share of spending on housing. I provide cross-sectional evidence that the secular rise of housing has been fully concentrated in states that are constrained by available land supply, whereas the ‘housing cost disease’ hypothesis of Borri and Reichlin (2015) would predict that it has occurred mainly in states experiencing fast manufacturing productivity growth. Moreover, the increase in the relative price of housing observed in most advanced economies occurred at a time when productivity growth in domestic manufacturing was slowing, which seems to argue against this version of events. In contrast, Davis and Ortalo-Magné (2011) outline a model that predicts that variation across cities in the relative price of housing is independent of housing supply conditions and depends purely on differences in average incomes. My results also contradict the predictions of that model. [2]
In 2014, the total value of the housing stock was estimated at US$18.9 trillion. The owner-occupied housing stock made up US$14.9 trillion (or 78.8 per cent of the total housing stock) while the tenant-occupied stock made up US$3.9 trillion (20.8 per cent). The tenant-occupied housing stock can be further divided by the type of owner into households (9.2 per cent of the total stock), sole proprietorships and partnerships (7.6 per cent), non-profit institutions (1.2 per cent) and corporates (1.0 per cent). The government-owned stock made up US$0.4 trillion (2.1 per cent). [3]
The FHFA provides housing price information for between 350 and 400 MSAs in the period since 1990 and between 150 and 350 MSAs for the period prior to 1990. [4]
Conventional mortgages are those that are neither insured nor guaranteed by the FHFA, the US Department of Veterans Affairs, or other federal government entities. Mortgages on properties financed by government-insured loans are excluded, as are properties with mortgages that exceed the conforming loan limit. Mortgage transactions on condominiums, cooperatives, multi-unit properties, and planned unit developments are also excluded. [5]
Given that the housing price estimates are based on transactions involving conforming mortgages there is likely to be sampling bias in using this housing price index (Garner and Verbrugge 2009). However, previous research has suggested that the direction of the bias is unclear, with both the lower and upper end of the housing market potentially being under-represented. Moreover, repeat-sale indices can suffer from renovation or ‘flip’ bias; renovations typically improve the quality of a home and lead to higher measured prices, so a repeat-sales index does not fully abstract from quality changes. [6]
The BLS estimates of the price of rent (both market and imputed) control for changes over time in dwelling characteristics, such as size and quality. So improvements in the quality of housing will show up as increases in the volume of housing services consumed. [7]
Interestingly, the national accounts indicate that the average age of the owner-occupied housing stock rose only slightly between 1925 and 2014 from 25.3 years to 26.5 years, while the average age of the tenant-occupied housing stock rose from 22.4 years to 41 years over the same period. It is not clear what is driving these different trends but they might be worth exploring in future research. [8]
A similar picture emerges if you instead use, say, the top 10 most inelastic states. [9]
This is a simplistic description of the user cost model. I ignore various complications associated with, for example, the tax deductibility of mortgage interest payments in the United States. I have estimated similar models that allow mortgage interest payments to be tax deductible (based on state-level information provided by the National Bureau of Economic Research's TAXSIM model). The TAXSIM model calculates federal and state income tax liabilities for each state and year from survey data. Based on this, it is possible to construct after-tax estimates of mortgage interest rates. However, these estimates complicate the interpretation of the models without adding much intuition. Saying that, the results are available upon request. [10]
The main regression results are not affected if I include additional state-level demographic controls such as the average household size and the age composition of the population. These results are available upon request. [11]
The model has also been estimated with quadratic time trends. The estimates are very similar to those of the model that includes the federal funds rate. [12]
The inclusion of year fixed effects in the specification for owner-occupier profits (column 6) results in the negative relationship between interest rates and profits being statistically insignificant at conventional levels. This is because there is more year-to-year variation in owner-occupier profits than in housing capital income and this variation is soaked up by the time dummies. [13]
Specifically, I assume the real interest rate (RINTRATE) is equal to the nominal interest rate (INTRATE) less CPI inflation (ΔCPI) divided by 1 plus CPI inflation. [14]
Disinflation facilitates an expansion of credit to the extent that the binding credit constraint is serviceability (the ratio of mortgage repayments to income) rather than leverage (the ratio of mortgage debt to home purchase price). See Ellis (2005) for more details. [15]
In Appendix C, I exploit a natural experiment based on the removal of interstate bank branching laws to provide more direct evidence that financial deregulation contributed to the secular rise in the share of housing capital income. [16]
Prior to 1994, eight states permitted some limited interstate branching (i.e., Alaska, Massachusetts, New York, Oregon, Rhode Island, Nevada, North Carolina and Utah). But the option to branch out of state lines was never exercised, except in a few cases. [17]
More specifically, there is information available on gross value added for the real estate sector by metro area but there are problems with BEA's methodology and its ability to measure GDP at the MSA level. GDP data is collected at the state level, not the metro level. The BEA allocates a state's GDP to metro areas using state-level GDP by industry and county-level earnings by industry. The state's GDP within each industry is allocated to counties based on county earnings data for each industry. The earnings of workers employed in the housing industry are likely to be a very imperfect proxy for the income earned by landlords and home owners. Moreover, the MSA-level data are only available since 2001, while most of the run-up in the share of housing income occurred prior to this period. [18]
The construction of the dummy variable for the deregulation (treatment) period allows me to interpret the estimated coefficients ‘more cleanly’ as average treatment effects. Alternatively, I could leave the regulation index in its original form, with values ranging from 0 to 4, and this would mean that the regulation index would still appear in the regression specification in first differences. This would implicitly place greater weight on states that retained multiple restrictions. For example, a state that retained two restrictions on bank branching would effectively experience a demand shock that was twice as large as that of a state that retained just one restriction. [19]
In unreported results, I find that the estimated treatment effect is not affected by excluding certain large states (e.g. California and New York). The results are also not affected if I include a wider range of control variables, such as the stock of housing, housing vacancy rates and demographics (e.g. population size, the age structure of the population). These results are available upon request. [20]